Mathematics
Use graph paper to answer this question.
During a medical checkup of 60 students in a school, weights were recorded as follows :
| Weight (in kg) | Number of students |
|---|---|
| 28-30 | 2 |
| 30-32 | 4 |
| 32-34 | 10 |
| 34-36 | 13 |
| 36-38 | 15 |
| 38-40 | 9 |
| 40-42 | 5 |
| 42-44 | 2 |
Taking 2 cm = 2 kg along one axis and 2 cm = 10 students along the other axis draw an ogive. Use your graph to find the :
(a) median
(b) upper quartile
(c) number of students whose weight is above 37 kg.
Statistics
ICSE 2023
11 Likes
Answer
(a)
| Weight (in kg) | Number of students (f) | Cumulative frequencies (c.f.) |
|---|---|---|
| 28-30 | 2 | 2 |
| 30-32 | 4 | 6 |
| 32-34 | 10 | 16 |
| 34-36 | 13 | 29 |
| 36-38 | 15 | 44 |
| 38-40 | 9 | 53 |
| 40-42 | 5 | 58 |
| 42-44 | 2 | 60 |
| Total | Σf = 60 |
Here, n = 60, which is even.
Median = th term = = 30th term.
Steps of construction :
Take 1 cm = 2 kg on x-axis.
Take 1 cm = 10 students on y-axis.
Since, x axis starts at 28 hence, a kink is drawn at the starting of x-axis. Plot the point (28, 0) as ogive starts on x-axis representing lower limit of first class.
Plot the points (30, 2), (32, 6), (34, 16), (36, 29), (38, 44), (40, 53), (42, 58) and (44, 60).
Join the points by a free-hand curve.
Draw a line parallel to x-axis from point A (no. of students) = 30, touching the graph at point B. From point B draw a line parallel to y-axis touching x-axis at point C.
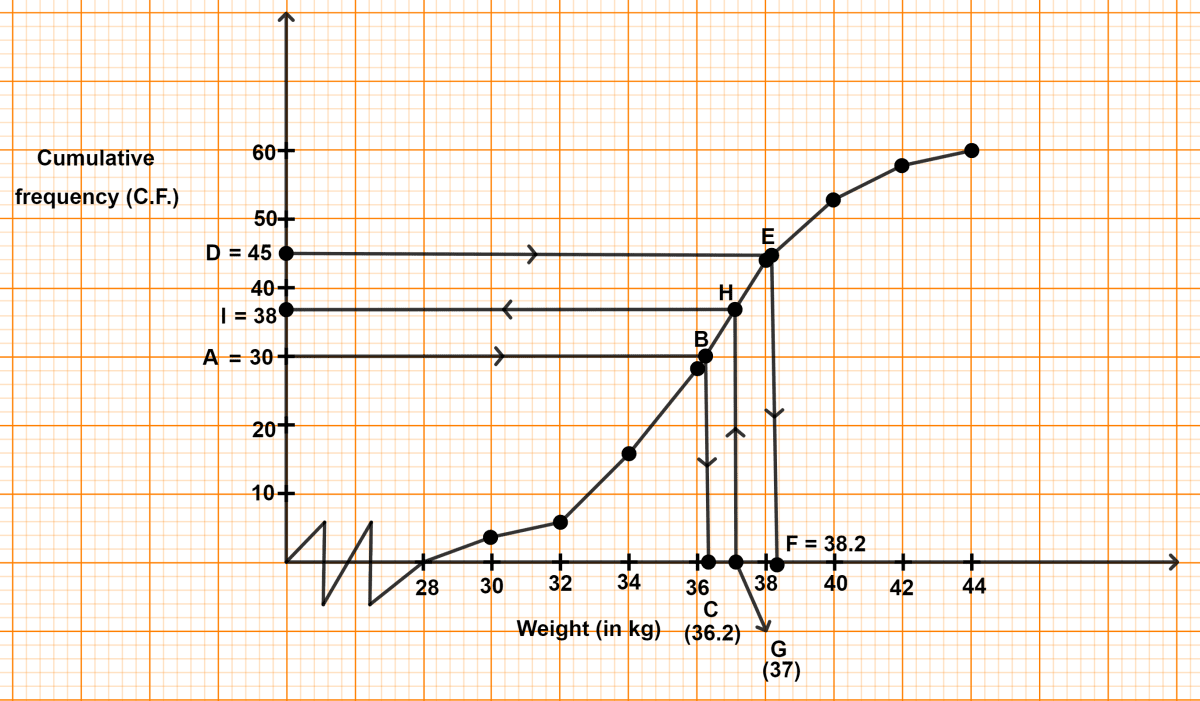
From graph, C = 36.2
Hence, median = 36.2 kg
(ii) Here, n = 60, which is even.
By formula,
Upper quartile = = 45th term.
Draw a line parallel to x-axis from point D (no. of students) = 45, touching the graph at point E. From point E draw a line parallel to y-axis touching x-axis at point F.
From graph, F = 38.2 kg
Hence, upper quartile = 38.2 kg.
(iii) Draw a line parallel to y-axis from point G (weight) = 37 kg, touching the graph at point H. From point H draw a line parallel to x-axis touching y-axis at point I.
From graph, I = 38.
∴ 38 students have weight less than or equal to 37 kg.
No. of students whose weight is more than 37 kg = 60 - 38 = 22.
Hence, no. of students whose weight is more than 37 kg = 22.
Answered By
6 Likes
Related Questions
Using componendo and dividendo solve for x : .
Which term of the Arithmetic Progression (A.P.) 15, 30, 45, 60 ….. is 300 ? Hence find the sum of all terms of the Arithmetic Progression (A.P.).
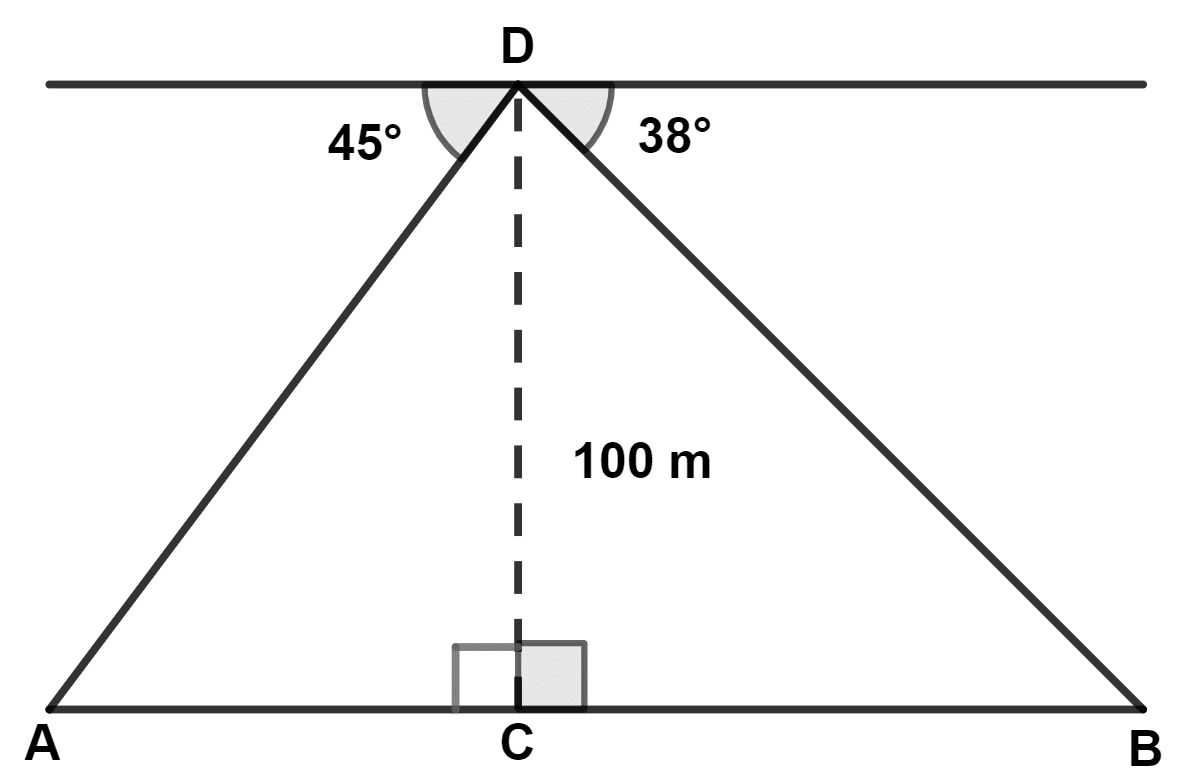
From the top of a tower 100 m high, a man observes the angle of depression of two ships A and B, on opposite sides of the tower as 45° and 38° respectively. If the foot of tower and the ships are in the same horizontal line, find the distance between two ships A and B to the nearest metre.
Factorize completely using factor theorem : 2x3 - x2 - 13x - 6.