Mathematics
Two circles touch each other externally at point P. OA and OB are the tangent of the two circles (as shown) and OA = 10 cm.
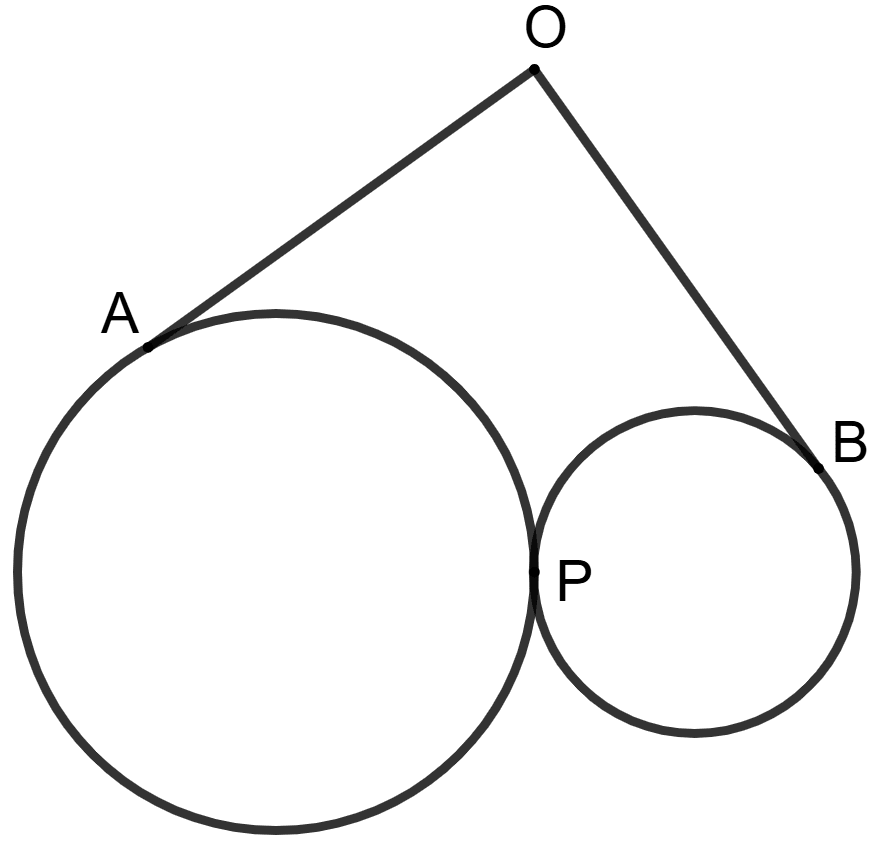
Statement (1): OB = 10 cm.
Statement (2): On joining O and P, tangent OP = tangent OA and tangent OP = tangent OB
Both the statement are true.
Both the statement are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Answer
Join OP.
We know that,
If two tangents are drawn to a circle from an exterior point, the tangents are equal in length.
From figure,
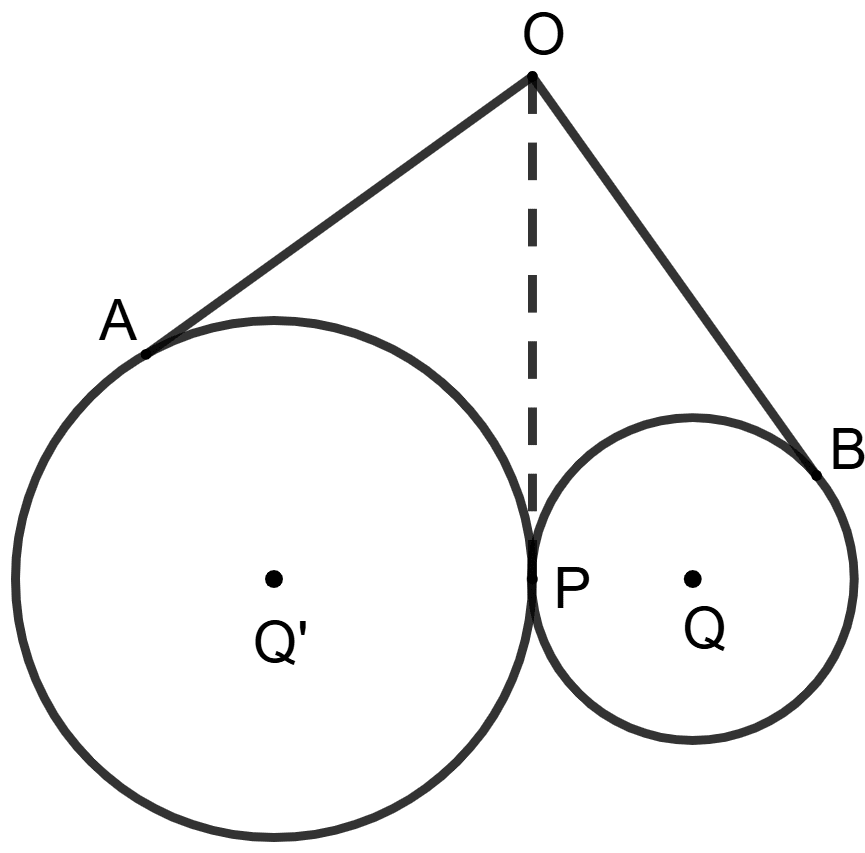
O is the point from which, OA and OP are two tangents to the circle with centre Q'.
So, OA = OP …….(1)
Similarly, from point O, OB and OP are two tangents to the circle with centre Q.
So, OB = OP ……(2)
From (1) and (2), we have
⇒ OA = OB
⇒ OB = 10 cm
∴ Both the statements are true.
Hence, option 1 is the correct option.
Related Questions
AB is diameter of the circle. PA is tangent and ∠AOC = 60°.
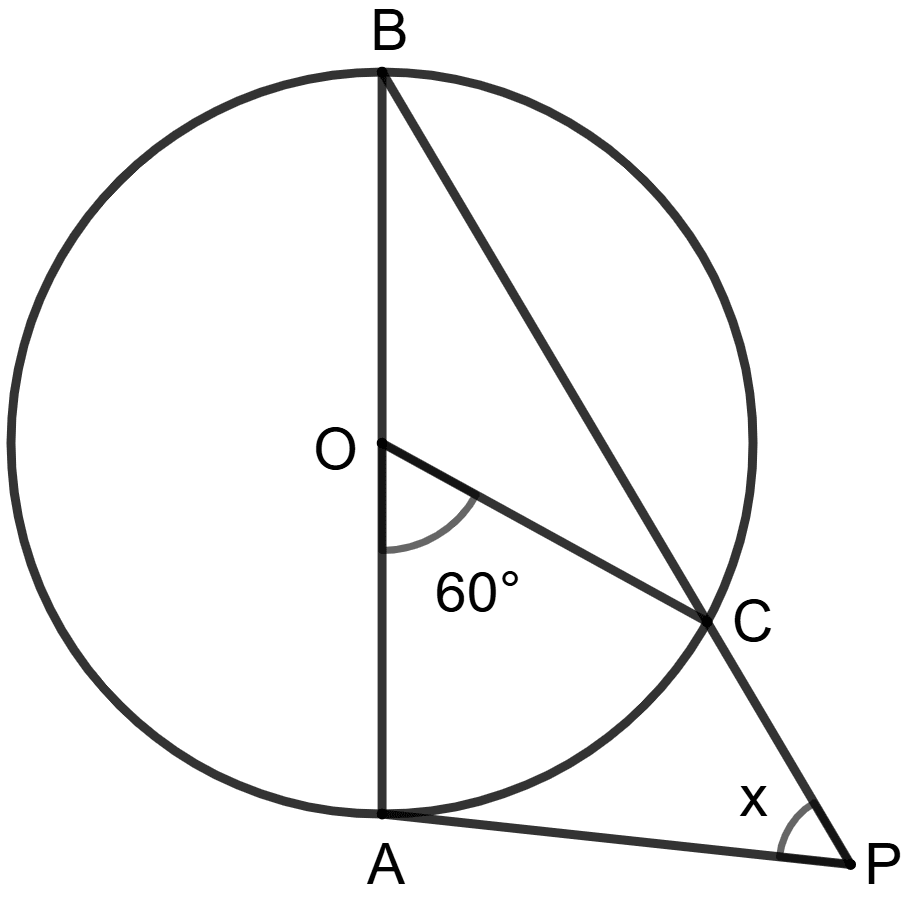
Assertion(A): x + 30° = 90°.
Reason(R): PA is tangent
⇒ ∠BAP = 90°
∴ x + 30° = 90°
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.
O is centre of the circle, PB and PC are tangents and ∠BPC = 50°.
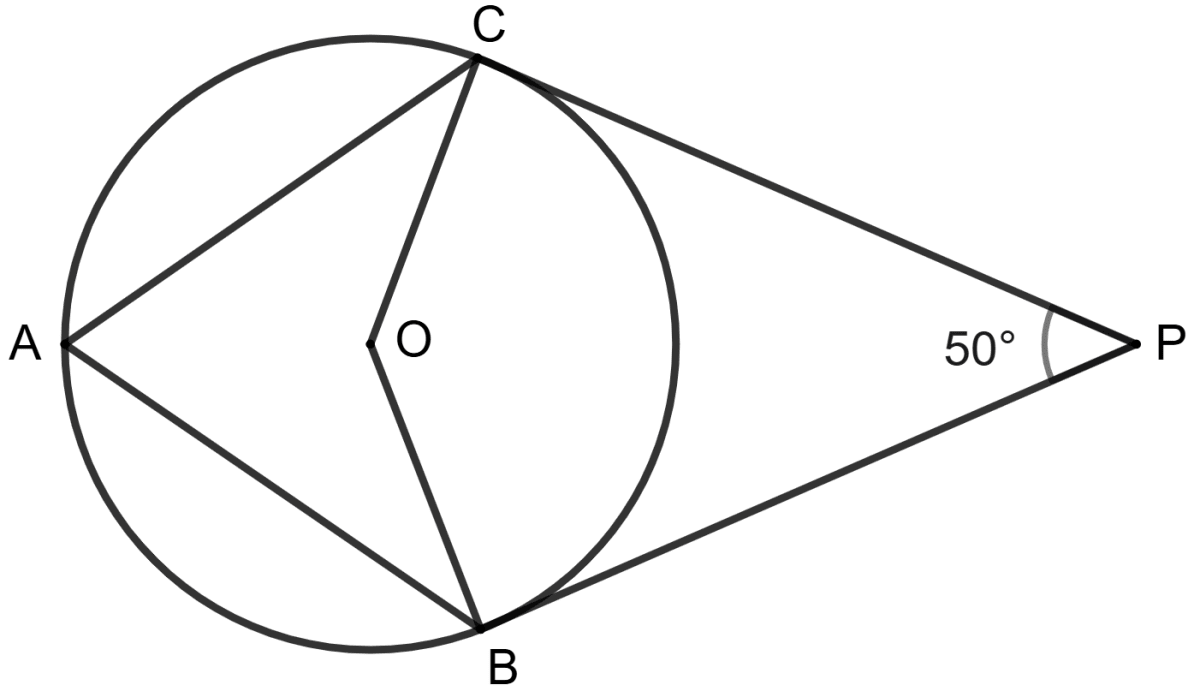
Statement (1): ∠BAC = ∠P = 50°
Statement (2): ∠BOC + 50° = 180°
⇒ ∠BOC = 130°
∴ ∠BAC = 65°
Both the statement are true.
Both the statement are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Prove that, of any two chords of a circle, the greater chord is nearer to the centre.