Mathematics
Use a graph paper for this question. A(1, 1), B(5, 1), C(4, 2) and D(2, 2) are the vertices of a quadrilateral.
(i) Name the quadrilateral ABCD.
(ii) A, B, C, D are reflected in the origin onto A', B', C' and D' respectively. Locate A', B', C', D' on the graph paper and write their co-ordinates.
(iii) Are D, A, A' and D' collinear?
Reflection
1 Like
Answer
The graph is shown below:
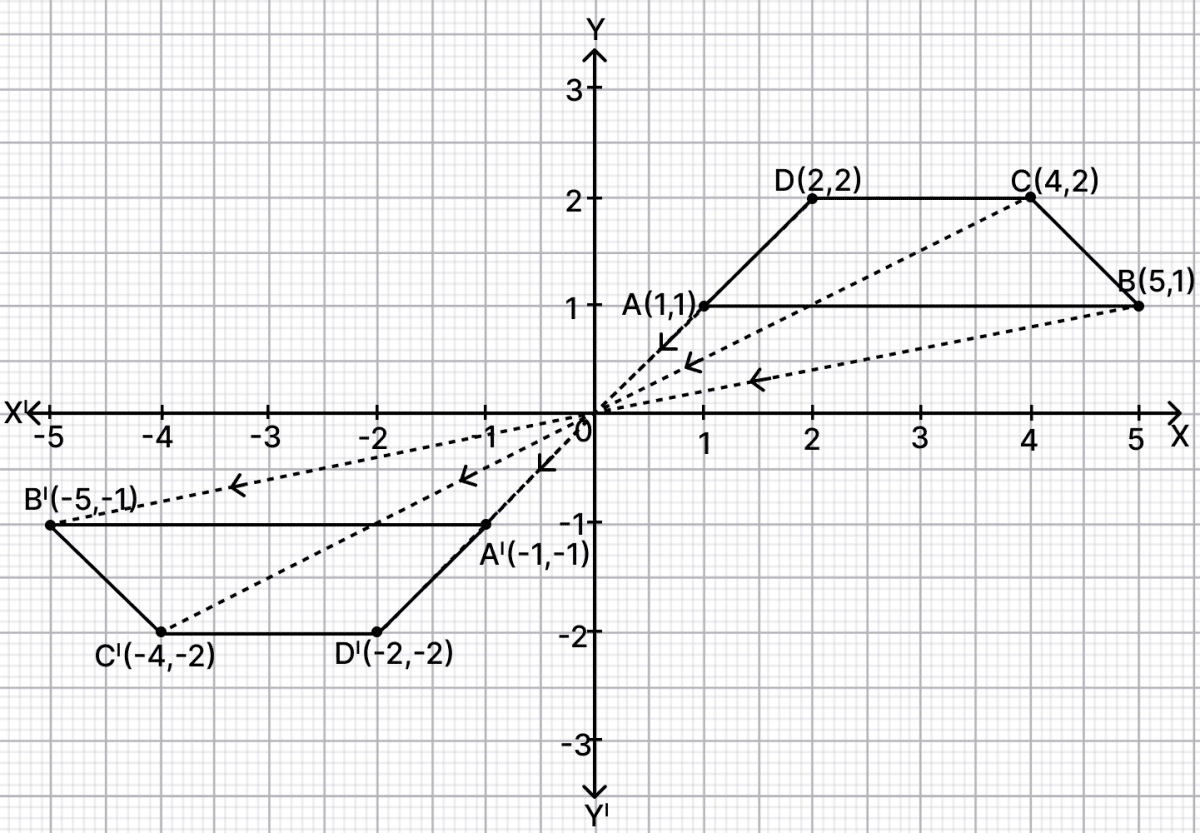
(i) From graph,
ABCD is an isosceles trapezium.
(ii) Reflect points A, B, C and D in origin.
Hence, A' = (-1, -1), B' = (-5, -1), C' = (-4, -2) and D' = (-2, -2).
(iii) From graph,
Points D, A, A' and D' lie on the same line i.e. y = x.
Hence, the points D, A, A' and D' collinear.
Answered By
2 Likes
Related Questions
Use a graph paper for this question. Plot the points P(3, 2) and Q(-3, -2). From P and Q, draw perpendiculars PM and QN on the x-axis.
(i) Name the image of P on reflection in the origin.
(ii) Assign the special name to the geometrical figure PMQN and find its area.
(iii) Write the co-ordinates of the point to which M is mapped on reflection in
(a) x-axis
(b) y-axis
(c) originThe point P(3, 4) is reflected to P' in x-axis and O' is the image of O (origin) when reflected in the line PP'.
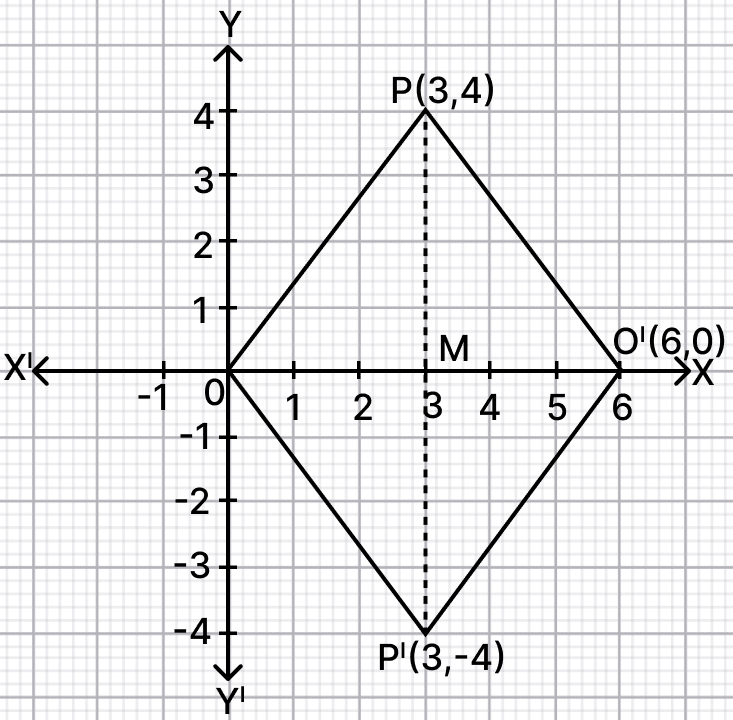
Using graph paper, give :
(i) the co-ordinates of P' and O'.
(ii) the length of the segments PP' and OO'.
(iii) the geometrical name of the figure POP'O'.
(iv) the perimeter of the quadrilateral POP'O'.
A ΔABC with vertices A(1, 2), B(4, 4) and C(3, 7) is first reflected in the line y = 0 onto ΔA'B'C' and then ΔA'B'C' is reflected in the origin onto ΔA"B"C".
Write down the co-ordinates of :
(i) A', B' and C'
(ii) A", B" and C"
Write down the single transformation that maps Δ ABC directly onto ΔA"B"C".
Use graph paper for this question.
The points A(2, 3), B(4, 5) and C(7, 2) are the vertices of ΔABC.
(i) Write down the co-ordinates of A', B', C' if ΔA'B'C' is the image of ΔABC when reflected in the origin.
(ii) Write down the co-ordinates of A", B", C" if ΔA"B"C" is the image of ΔABC when reflected in the x-axis.
(iii) Mention the special name of the quadrilateral BCC"B" and find its area.