Mathematics
Use ruler and compass for the following construction. Construct a ΔABC, where AB = 6 cm, AC = 4.5 cm and ∠BAC = 120°. Construct a circle circumscribing the ΔABC. Measure and write down the length of the radius of the circle.
Answer
Given,
AB = 6 cm, AC = 4.5 cm and ∠BAC = 120°
Steps of construction,
Draw a line segment AB = 6 cm.
Construct ∠BAY = 120°.
With A as center and radius equal to 4.5 cm draw an arc intersecting AY at C.
Join points B and C.
Draw the perpendicular bisectors of AB and AC. The point where the two perpendicular bisectors intersect is the center of the circumscribing circle. Mark this point as O.
Measure OC, with O as center and OC as radius, construct a circle passing through points A, B and C.
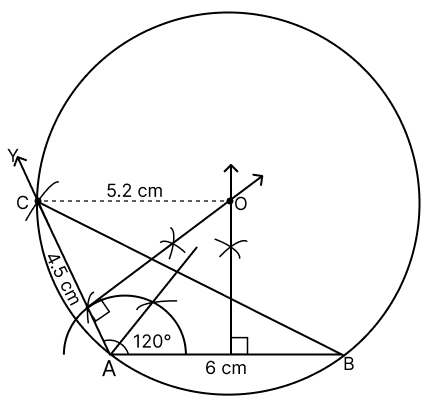
On measuring, we get :
OC = 5.2 cm
Hence, radius of circle = 5.2 cm.
Related Questions
Mrs. Rao deposited ₹ 250 per month in a recurring deposit account for a period of 3 years. She received ₹ 10,110 at the time of maturity. Find:
(a) the rate of interest.
(b) how much more interest Mrs. Rao will receive if she had deposited ₹50 more per month at the same rate of interest and for the same time.
In ΔABC, ∠ABC = 90°, AB = 20 cm, AC = 25 cm, DE is perpendicular to AC such that ∠DEA = 90° and DE = 3 cm as shown in the given figure.
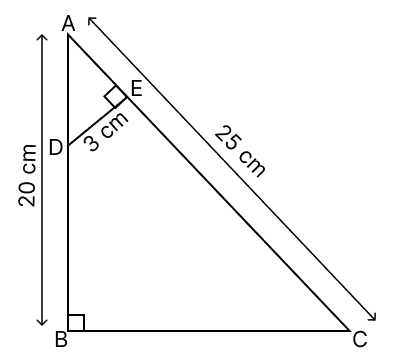
(a) Prove that ΔABC ~ ΔAED.
(b) Find the lengths of BC, AD and AE.
(c) If BCED represents a plot of land on a map whose actual area on ground is 576 m2, then find the scale factor of the map.
In the given graph ABCD is a parallelogram.
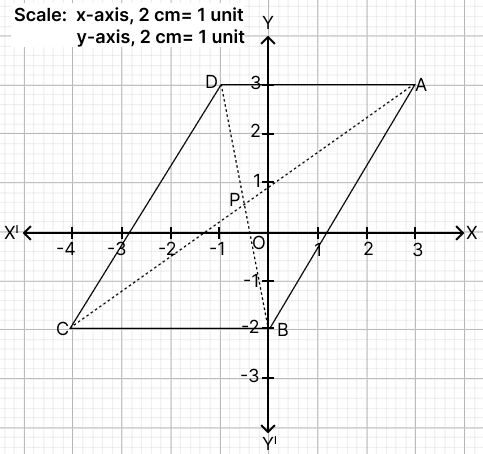
Using the graph, answer the following:
(a) write down the coordinates of A, B, C and D.
(b) calculate the coordinates of ‘P’, the point of intersection of the diagonals AC and BD.
(c) find the slope of sides CB and DA and verify that they represent parallel lines.
(d) find the equation of the diagonal AC.