Mathematics
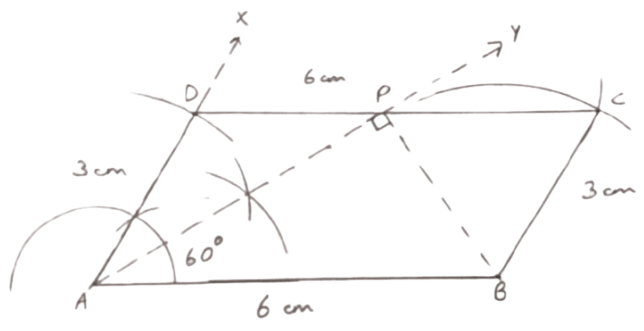
Using ruler and compasses only, construct a parallelogram ABCD, in which: AB = 6 cm, AD = 3 cm and ∠DAB = 60°.
In the same figure draw the bisector of angle DAB and let it meet DC at point P. Measure angle APB.
Answer
Steps:
Draw a line segment AB = 6 cm.
At A, construct angle XAB = 60° and from XA cut AD = 3 cm.
Taking B as center, draw an arc of radius 3 cm (= AD) and taking D as center draw one more arc of radius 6 cm (= AB). Let the two arcs intersect at point C.
Join BC and DC. Hence, ABCD is the required parallelogram.
Draw AY, the angle bisector of A.
Mark point P as the intersection of line AY and DC.
Join PB. Measure ∠APB.
Hence, ∠APB = 90°.
Related Questions
Construct a rhombus ABCD, if:
BC = 4.8 cm and diagonal AC = 7 cm.
Construct a rhombus ABCD, if:
diagonal AC = 6.6 cm and diagonal BD = 5.8 cm.
Let angle ABC = 60° and angle ABD = 90°, then ∠CBD is equal to:
150°
30°
150° or 30°
none of these
The shortest distance between the point P and the line segment AB is:
PA
PB
line joining point P with the mid-point of AB.
length of perpendicular from point P to line AB.