Mathematics
where x ∈ R.
Assertion (A): The largest value of x is .
Reason (R): When the signs of both the sides of an inequalities are changed, the sign of inequality reverses.
A is true, R is false.
A is false, R is true.
Both A and R are true and R is the correct reason for A.
Both A and R are true and R is the incorrect reason for A.
Linear Inequations
3 Likes
Answer
Both A and R are true and R is the correct reason for A.
Reason
According to the assertion:
So, Assertion (A) is true.
According to the reason:
When you multiply or divide both sides of an inequality by a negative number, the direction of the inequality sign must be reversed to maintain the validity of the inequality
So, Reason (R) is true.
Hence, option 3 is correct.
Answered By
2 Likes
Related Questions
The real number lines for two inequations A and B are as given below, A ∩ B is :
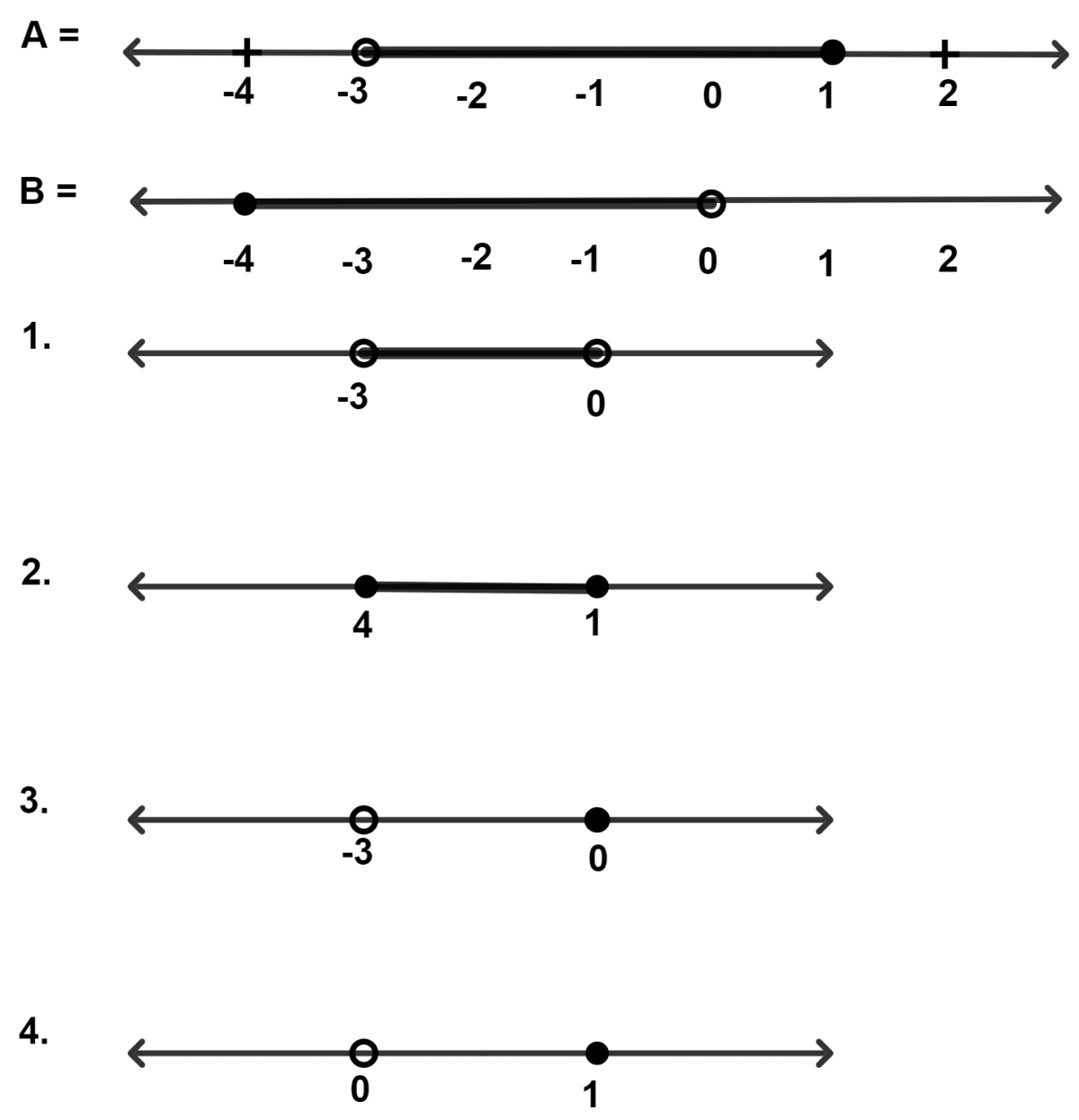
For the inequations A and B [as given above in part (d)], A ∪ B is :
![For the inequations A and B [as given above in part (d)], A ∪ B is : Linear Inequations, Concise Mathematics Solutions ICSE Class 10.](https://cdn1.knowledgeboat.com/img/cm10/q1-e-test-linear-inequations-maths-concise-icse-class-10-solutions-1126x1099.png)
Inequation 5 - 2x ≥ x - 10, where x ∈ N (Natural numbers)
Assertion (A): 5 - 2x ≥ x - 10 ⇒ -3x ≥ -15 ⇒ x ≥ 5
∴ Solution set = {5, 6, 7, 8, ……….}
Reason (R): 5 - 2x ≥ x - 10 ⇒ 5 + 10 ≥ 3x ⇒ x ≤ 5
∴ Solution set = {1, 2, 3, 4, 5}
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.
x ∈ W, x ≥ -3 and x < 5.
Statement (1) : There will be no solution for the given inequalities.
Statement (2) : The real number line for the given inequations is :

Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.