Pythagoras Theorem

Lengths of sides of triangle are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse:

(i) 3 cm, 8 cm, 6 cm

(ii) 13 cm, 12 cm, 5 cm

(iii) 1.4 cm, 4.8 cm, 5 cm

Answer

Choose the greatest length. Check whether the square of greatest length is equal to the sum of squares of other two lengths.

(i) Here greatest length is 8 cm and other lengths are 3 cm, 6 cm.

Note that 8² = 64 and 3² + 6² = 9 + 36 = 45.

Note that, 64 ≠ 45.

Hence, the triangle with given lengths of sides is not a right triangle.

(ii) Here greatest length is 13 cm and other lengths are 5 cm, 12 cm.

Note that 13² = 169 and 5² + 12² = 25 + 144 = 169.

Thus, 13² = 5² + 12².

Hence, the triangle with given lengths of sides is a right triangle and length of hypotenuse is 13 cm.

(iii) Here greatest length is 5 cm and other lengths are 1.4 cm, 4.8 cm.

Note that 5² = 25 and (4.8)² + (1.4)² = 23.04 + 1.96 = 25.

Thus, 5² = (4.8)² + (1.4)².

Hence, the triangle with given lengths of sides is a right triangle and length of hypotenuse is 5 cm.

Foot of a 10 m long ladder leaning against a vertical well is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.

Answer

Let AB be the ladder and BC be the vertical well.

So, △ABC is right triangle.

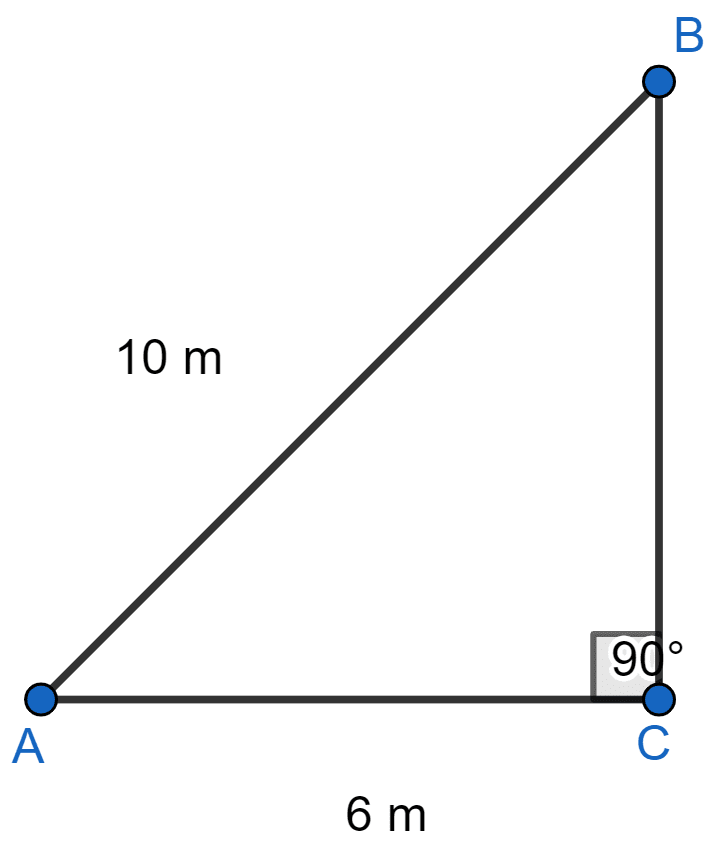
By pythagoras theorem,

⇒ AB² = BC² + AC²

⇒ 10² = BC² + (6)²

⇒ 100 = BC² + 36

⇒ BC² = 100 - 36 = 64

⇒ BC = $\sqrt{64}$ = 8 m.

Hence, the top of the ladder reaches 8 m above the wall of well.

A guy attached a wire 24 m long to a vertical pole of height 18 m and has a stake attached to other end. How far from the base of the pole should the stake be driven so that the wire will be taught ?

Answer

Let BC be the pole and AB be the wire and let the distance of stake from base of pole be x.

Since, pole is vertical so △ABC is right triangle.

By pythagoras theorem,

⇒ AB² = BC² + AC²

⇒ 24² = 18² + x²

⇒ 576 = x² + 324

⇒ x² = 576 - 324 = 252

⇒ x = $\sqrt{252} = 6\sqrt{7}$ m.

Hence, the stake should be at a distance of $6\sqrt{7}$ m from the base of the pole.

Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between their feet is 12 m, find the distance between their tops.

Answer

Let AB be the smaller pole and CD the bigger pole.

From figure,

⇒ CE = AB = 6 m and AE = BC = 12 m

⇒ CD = CE + ED

⇒ 11 = 6 + ED

⇒ ED = 5 m

From figure,

△ADE is right triangle.

By pythagoras theorem,

⇒ AD² = AE² + ED²

⇒ AD² = (12)² + (5)²

⇒ AD² = 144 + 25

⇒ AD² = 169

⇒ AD = $\sqrt{169}$ = 13 m.

Hence, the distance between tops of poles is 13 m.

In a right-angled triangle, if hypotenuse is 20 cm and the ratio of the other sides is 4 : 3, find the sides.

Answer

Ratio of other two sides = 4 : 3

Let other sides be 4x cm and 3x cm.

By pythagoras theorem,

⇒ 20² = (4x)² + (3x)²

⇒ 400 = 16x² + 9x²

⇒ 400 = 25x²

⇒ x² = $\dfrac{400}{25}$

⇒ x² = 16

⇒ x = 4

Sides ⇒ 4x = 16 cm and 3x = 12 cm.

Hence, the sides are 12 cm and 16 cm.

If the sides of the triangle are in the ratio 3 : 4 : 5, prove that it is right-angled triangle.

Answer

Ratio of sides = 3 : 4 : 5

Let sides be 3x, 4x and 5x cm.

Here, greatest length is 5x cm and other lengths are 3x cm, 4x cm.

Note that (5x)² = 25x² and (3x)² + (4x)² = 9x² + 16x² = 25x².

Thus, (5x)² = (3x)² + (4x)².

Hence, proved that triangle having sides in the ratio 3 : 4 : 5 is a right-angle triangle.

For going to a city B from the city A, there is route via city C such that AC ⊥ CB. AC = 2x km and CB = 2(x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of highway.

Answer

From figure,

△ABC is right triangle.

By pythagoras theorem,

⇒ AB² = AC² + BC²

⇒ 26² = (2x)² + [2(x + 7)]²

⇒ 676 = 4x² + (2x + 14)²

⇒ 676 = 4x² + 4x² + 196 + 56x

⇒ 676 - 196 = 8x² + 56x

⇒ 8x² + 56x = 480

⇒ 8(x² + 7x) = 480

⇒ x² + 7x = 60

⇒ x² + 7x - 60 = 0

⇒ x² + 12x - 5x - 60 = 0

⇒ x(x + 12) - 5(x + 12) = 0

⇒ (x - 5)(x + 12) = 0

⇒ x = 5 or x = -12.

Since, distance cannot be negative so, x ≠ -12.

Distance taken to reach from B to A without highway = BC + AC

= 2(x + 7) + 2x

= 2x + 14 + 2x

= 4x + 14

= 4(5) + 14

= 20 + 14 = 34 km

Distance taken to reach from B to A through highway = 26 km

Distance saved = 34 - 26 = 8 km.

Hence, 8 km will be saved in reaching city A from B after construction of highway.

The hypotenuse of a right triangle is 6 m more than twice the shortest side. If the third side is 2m less than the hypotenuse, find the sides of the triangle.

Answer

Let the shortest side be x meters.

Hypotenuse = 2x + 6 meters

Third side = 2x + 6 - 2 = 2x + 4 meters.

Since, the sides are of a right triangle.

By pythagoras theorem,

⇒ (Hypotenuse)² = (First Side)² + (Second side)²

⇒ (2x + 6)² = (x)² + (2x + 4)²

⇒ 4x² + 36 + 24x = x² + 4x² + 16 + 16x

⇒ 4x² + 36 + 24x = 5x² + 16 + 16x

⇒ 5x² - 4x² + 16x - 24x + 16 - 36 = 0

⇒ x² - 8x - 20 = 0

⇒ x² - 10x + 2x - 20 = 0

⇒ x(x - 10) + 2(x - 10) = 0

⇒ (x + 2)(x - 10) = 0

⇒ x = -2 or x = 10.

Since, side cannot be negative,

x ≠ -2.

Shortest side = 10 m

Hypotenuse = 2x + 6 = 2(10) + 6 = 26 m

Third side = 2x + 4 = 2(10) + 6 = 24 m.

Hence, sides of triangle = 10 m, 24 m and 26 m.

ABC is an isosceles triangle right angled at C. Prove that AB² = 2AC².

Answer

Since, the triangle is right triangle.

Hence, the side opposite to right angle will be hypotenuse and will be the greatest side.

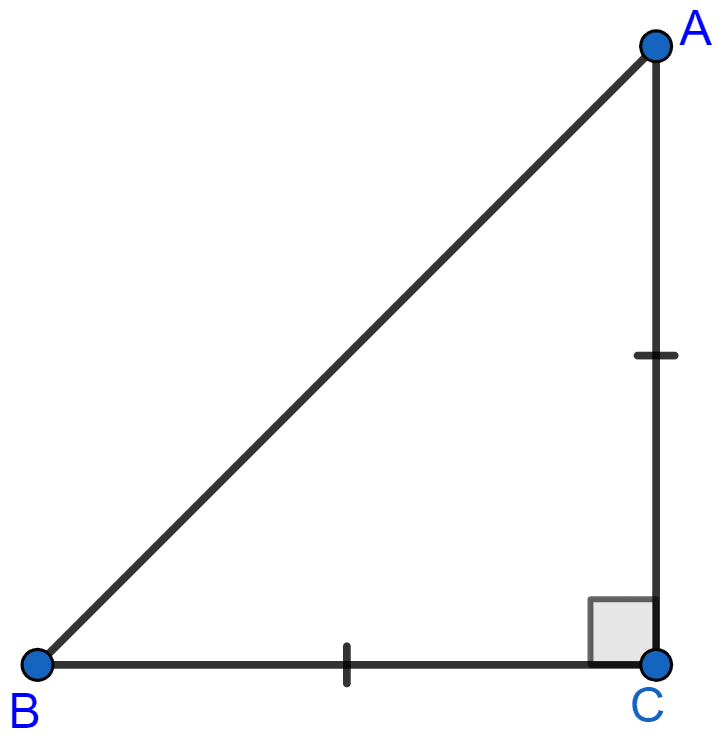
From figure,

Hypotenuse = AB.

The other two sides will be equal as the triangle is also isosceles i.e. (AC = BC)

By pythagoras theorem,

⇒ (AB)² = (AC)² + (BC)²

⇒ (AB)² = (AC)² + (AC)²

⇒ (AB)² = 2AC².

Hence, proved that (AB)² = 2AC².

In a triangle ABC, AD is perpendicular to BC. Prove that AB² + CD² = AC² + BD².

Answer

From figure,

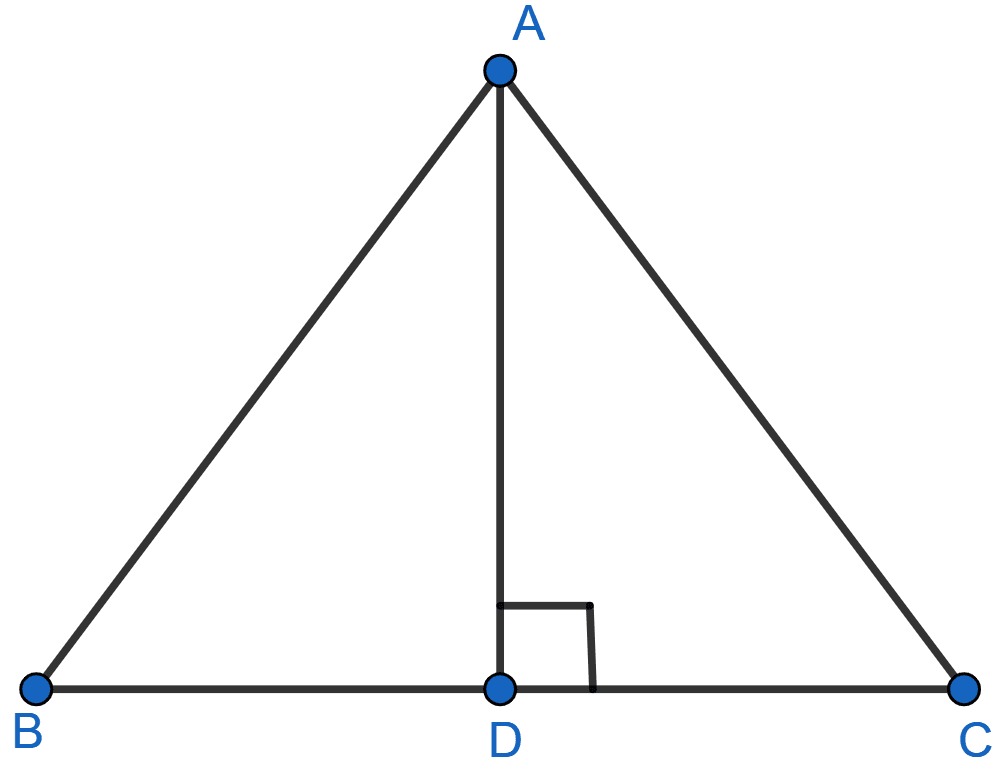
Considering right triangle ABD,

By pythagoras theorem,

AB² = AD² + BD² .......(1)

Considering right triangle ACD,

By pythagoras theorem,

AC² = AD² + CD² .......(2)

Subtracting eqn. 2 from 1 we get,

⇒ AB² - AC² = AD² + BD² - AD² - CD²

⇒ AB² - AC² = BD² - CD²

⇒ AB² + CD² = BD² + AC².

Hence, proved that AB² + CD² = AC² + BD².

In △PQR, PD ⊥ QR such that D lies on QR. If PQ = a, PR = b, QD = c and DR = d, prove that (a + b)(a - b) = (c + d)(c - d).

Answer

In right angle △PDQ,

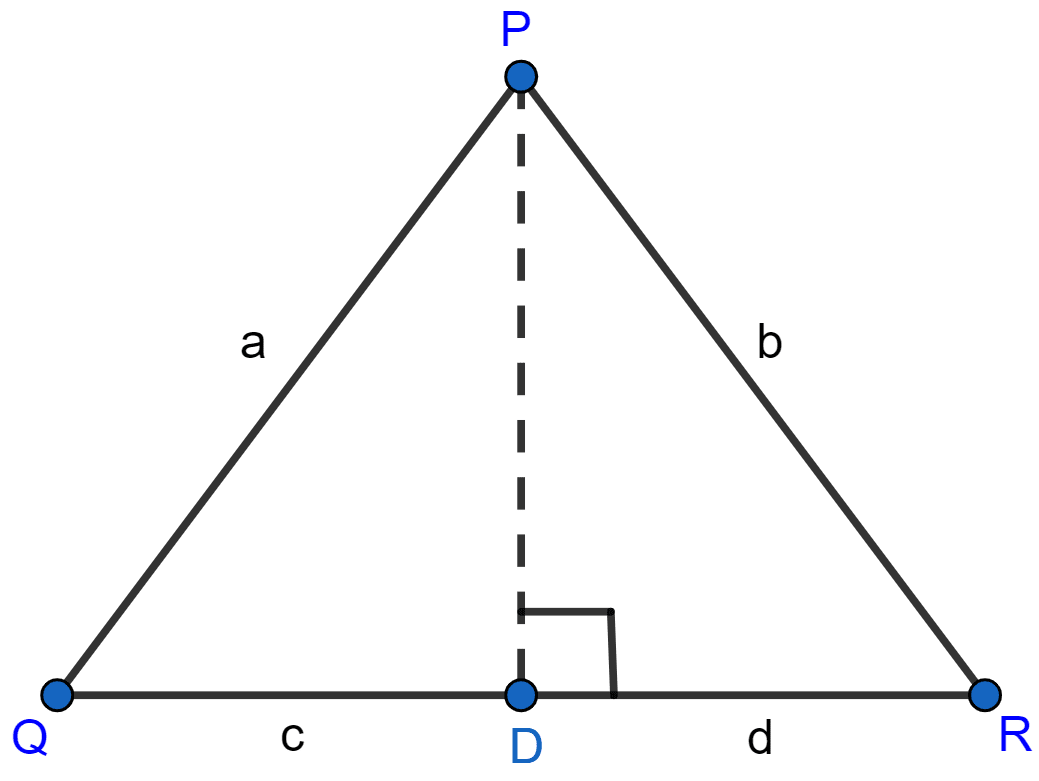
By pythagoras theorem we get,

⇒ PQ² = PD² + QD²

⇒ a² = PD² + c²

⇒ PD² = a² - c² ........(i)

In right angle △PDR,

By pythagoras theorem we get,

⇒ PR² = PD² + DR²

⇒ b² = PD² + d²

PD² = b² - d² ........(ii)

From (i) and (ii) we get,

⇒ a² - c² = b² - d²

⇒ a² - b² = c² - d²

⇒ (a - b)(a + b) = (c - d)(c + d).

Hence, proved that (a - b)(a + b) = (c - d)(c + d).

ABC is an isosceles triangle with AB = AC = 12 cm and BC = 8 cm. Find the altitude on BC and hence calculate its area.

Answer

Let AD be altitude on BC and BD = x cm and CD = (8 - x) cm.

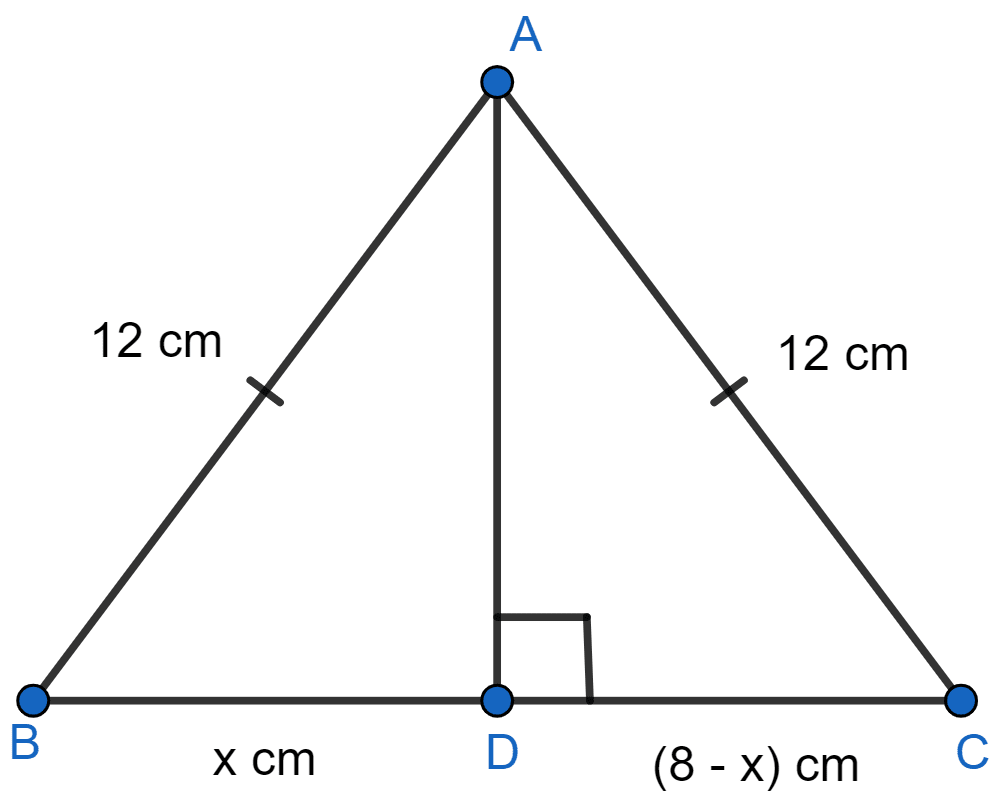
From figure,

In right angle △ABD,

By pythagoras theorem,

AB² = AD² + BD²

12² = AD² + x²

AD² = 12² - x² ........(i)

In right angle △ADC,

By pythagoras theorem,

AC² = AD² + DC²

12² = AD² + (8 - x)²

AD² = 12² - (8 - x)² ........(ii)

From (i) and (ii) we get,

12² - x² = 12² - (8 - x)²

144 - x² = 144 - (64 + x² - 16x)

144 - x² = 144 - 64 - x² + 16x

144 - 144 - x² + x² + 64 = 16x

16x = 64

x = 4.

Substituting value of x in (i) we get,

AD² = 12² - x² = 144 - (4)² = 144 - 16 = 128

AD² = 128

AD = $\sqrt{128} = 8\sqrt{2}$ cm.

Area = $\dfrac{1}{2} \times AD \times BC = \dfrac{1}{2} \times 8\sqrt{2} \times 8 = 32\sqrt{2}$ cm².

Hence, AD = $8\sqrt{2}$ cm and area = $32\sqrt{2}$ cm².

Find the area and the perimeter of a square whose diagonal is 10 cm long.

Answer

Let each side of square be a cm.

Since, sides of square are perpendicular to each other,

In right angle △ABC,

By pythagoras theorem,

⇒ AC² = AB² + BC²

⇒ 10² = a² + a²

⇒ 100 = 2a²

⇒ a² = 50

⇒ a = $\sqrt{50} = 5\sqrt{2}$ cm.

Perimeter = 4a = $20\sqrt{2}$ cm.

Area = a² = 50 cm².

Hence, perimeter = $20\sqrt{2}$ cm and area = 50 cm².

In figure given below, ABCD is a quadrilateral in which AD = 13 cm, DC = 12 cm, BC = 3 cm, ∠ABD = ∠BCD = 90°. Calculate the length of AB.

Answer

In right angle △DBC,

By pythagoras theorem,

⇒ DB² = DC² + BC²

⇒ DB² = 12² + 3²

⇒ DB² = 144 + 9

⇒ DB² = 153.

⇒ DB = $\sqrt{153}$.

In right angle △ABD,

By pythagoras theorem,

⇒ AD² = AB² + DB²

⇒ 13² = AB² + 153

⇒ 169 - 153 = AB²

⇒ AB² = 16

⇒ AB = $\sqrt{16}$ = 4 cm.

Hence, AB = 4 cm.

In figure given below, ABCD is a quadrilateral in which AB = AD, ∠A = 90° = ∠C, BC = 8 cm and CD = 6 cm. Find AB and calculate the area of △ABD.

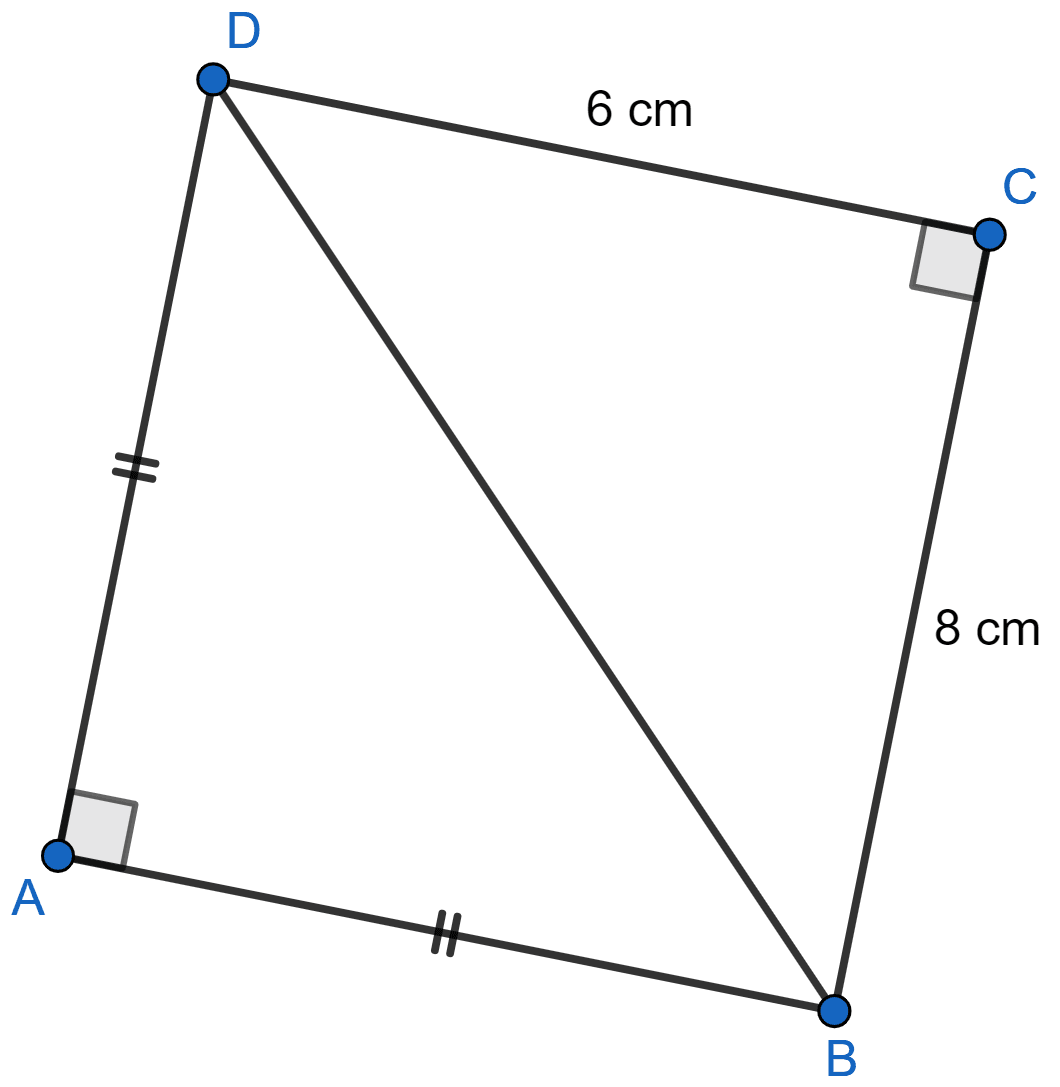
Answer

Let AB = AD = x cm.

In right angle △BCD,

By pythagoras theorem,

⇒ BD² = BC² + CD²

⇒ BD² = 8² + 6²

⇒ BD² = 64 + 36

⇒ BD² = 100

⇒ BD = $\sqrt{100}$ = 10 cm.

In right angle △ABD,

By pythagoras theorem,

⇒ BD² = AB² + AD²

⇒ 10² = x² + x²

⇒ 100 = 2x²

⇒ x² = 50

⇒ x = $\sqrt{50} = 5\sqrt{2}$ cm.

Area of right angle △ABD

$= \dfrac{1}{2} \times \text{base} \times \text{ height} \\[1em] = \dfrac{1}{2} \times AB \times AD \\[1em] = \dfrac{1}{2} \times 5\sqrt{2} \times 5\sqrt{2} \\[1em] = 25 \text{ cm}^2.$

Hence, AB = $5\sqrt{2}$ cm and area of right angle △ABD = 25 cm².

In figure given below, AB = 12 cm, AC = 13 cm, CE = 10 cm and DE = 6 cm. Calculate the length of BD.

Answer

In right angle △ABC,

By pythagoras theorem,

⇒ AC² = AB² + BC²

⇒ 13² = 12² + BC²

⇒ BC² = 13² - 12²

⇒ BC² = 169 - 144 = 25

⇒ BC = $\sqrt{25}$ = 5 cm.

In right angle △CDE,

By pythagoras theorem,

⇒ CE² = CD² + DE²

⇒ 10² = CD² + 6²

⇒ CD² = 10² - 6²

⇒ CD² = 100 - 36 = 64

⇒ CD = $\sqrt{64}$ = 8 cm.

From figure,

BD = BC + CD = 5 + 8 = 13 cm.

Hence, BD = 13 cm.

In figure given below, ∠PSR = 90°, PQ = 10 cm, QS = 6 cm and RQ = 9 cm. Calculate the length of PR.

Answer

In right angle △PQS,

By pythagoras theorem,

⇒ PQ² = PS² + QS²

⇒ 10² = PS² + 6²

⇒ PS² = 10² - 6²

⇒ PS² = 100 - 36 = 64

⇒ PS = $\sqrt{64}$ = 8 cm.

From figure,

RS = RQ + QS = 9 + 6 = 15 cm.

In right angle △PRS,

By pythagoras theorem,

⇒ PR² = RS² + PS²

⇒ PR² = 15² + 8²

⇒ PR² = 225 + 64

⇒ PR² = 289

⇒ PR = $\sqrt{289}$ = 17 cm.

Hence, PR = 17 cm.

In figure given below, ∠D = 90°, AB = 16 cm, BC = 12 cm and CA = 6 cm. Find CD.

Answer

Let CD be x cm.

In right angle △ACD,

By pythagoras theorem,

⇒ AC² = AD² + CD²

⇒ 6² = AD² + x²

⇒ AD² = 36 - x² .......(i)

In right angle △ABD,

By pythagoras theorem,

⇒ AB² = AD² + BD²

⇒ 16² = (36 - x²) + (12 + x)²

⇒ 256 = 36 - x² + 144 + x² + 24x

⇒ 256 = 180 + 24x

⇒ 24x = 76

⇒ x = $\dfrac{76}{24} = 3\dfrac{1}{6}$ cm.

Hence, CD = $3\dfrac{1}{6}$ cm.

In figure given below, BC = 5 cm, ∠B = 90°, AB = 5AE, CD = 2AE and AC = ED. Calculate the lengths of EA, CD, AB and AC.

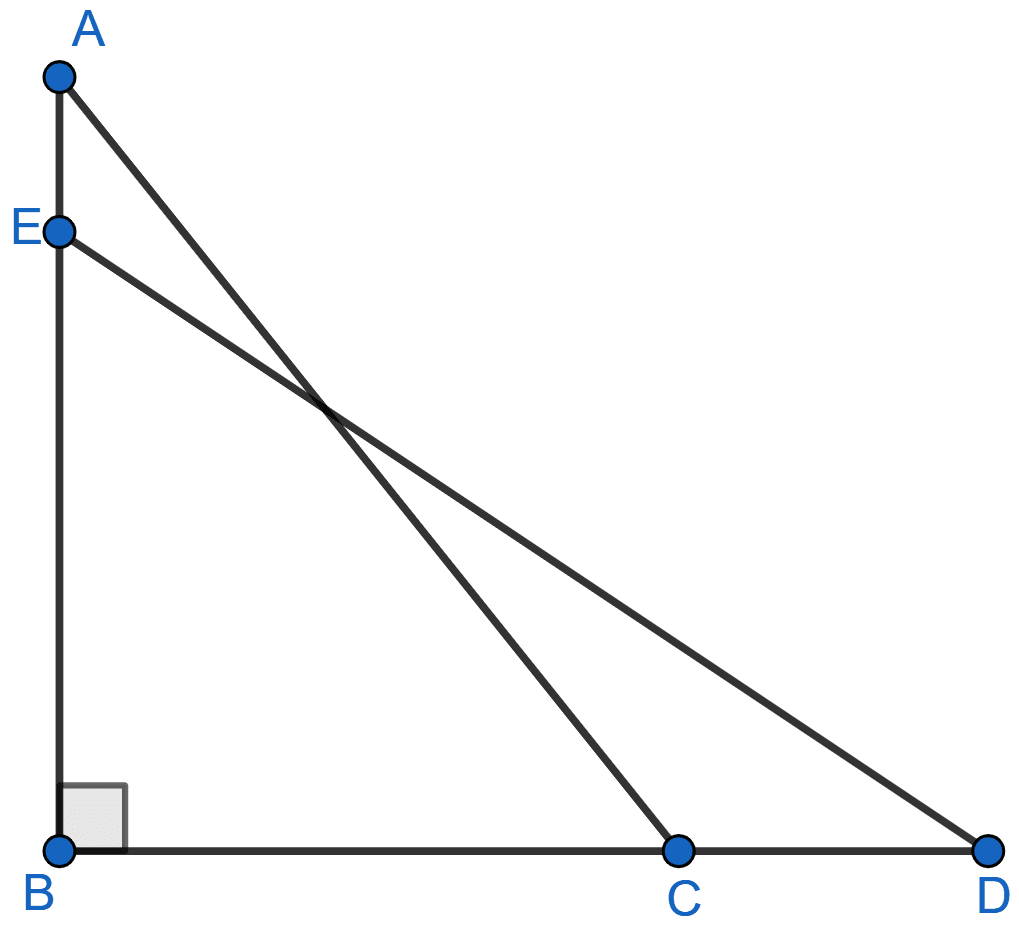
Answer

In right angle △ABC,

By pythagoras theorem,

⇒ AC² = AB² + BC²

⇒ AC² = (5AE)² + 5²

⇒ AC² = 25AE² + 25

⇒ AC² = 25(AE² + 1) .......(i)

From figure,

EB = AB - AE = 5AE - AE = 4AE.

In right angle △BED,

⇒ ED² = EB² + BD²

⇒ ED² = (4AE)² + (5 + 2AE)²

⇒ ED² = 16AE² + 25 + 4AE² + 20AE

⇒ ED² = 20AE² + 20AE + 25 .......(ii)

Given, AC = ED.

∴ From (i) and (ii) we get,

⇒ 25(AE² + 1) = 20AE² + 20AE + 25

⇒ 25AE² + 25 = 20AE² + 20AE + 25

⇒ 25AE² - 20AE² - 20AE + 25 - 25 = 0

⇒ 5AE² - 20AE = 0

⇒ 5AE(AE - 4) = 0

⇒ 5AE = 0 or AE - 4 = 0

⇒ AE = 0 or AE = 4 cm.

Since, side cannot be 0 so AE ≠ 0.

AE = 4 cm,

CD = 2AE = 8 cm,

AB = 5AE = 20 cm,

Substituting value of AE in (i) we get,

⇒ AC² = 25(AE² + 1)

⇒ AC² = 25(4² + 1)

⇒ AC² = 25(16 + 1) = 25 × 17 = 425

⇒ AC = $\sqrt{425} = 5\sqrt{17}$ cm.

Hence, EA = 4 cm, CD = 8 cm, AB = 20 cm and AC = $5\sqrt{17}$ cm.

In figure given below, ABC is a right triangle right angled at C. If D is mid-point of BC, prove that AB² = 4AD² - 3AC².

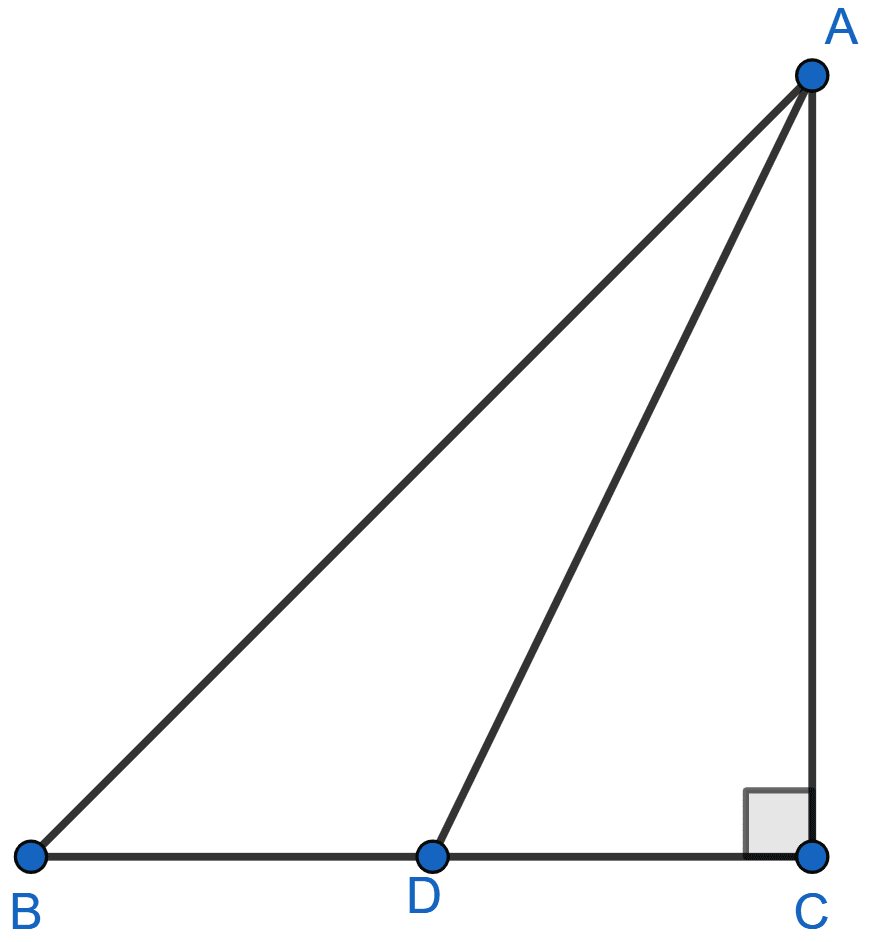
Answer

Since, D is mid-point of BC so we get,

DC = $\dfrac{BC}{2}$.

ABC is a right triangle.

By pythagoras theorem,

⇒ AB² = AC² + BC² .......(i)

ADC is a right triangle.

By pythagoras theorem,

⇒ AD² = AC² + DC² .......(ii)

⇒ AC² = AD² - DC²

⇒ AC² = AD² - $\Big(\dfrac{1}{2}\text{BC}\Big)^2$

⇒ AC² = AD² - $\dfrac{1}{4}\text{BC}^2$

⇒ AC² = $\dfrac{4\text{AD}^2 - \text{BC}^2}{4}$

⇒ 4AC² = 4AD² - BC²

⇒ AC² + 3AC² = 4AD² - BC²

⇒ AC² + BC² = 4AD² - 3AC²

⇒ AB² = 4AD² - 3AC² [....From (i)]

Hence, proved that AB² = 4AD² - 3AC².

In △ABC, AB = AC = x, BC = 10 cm and the area of △ABC is 60 cm². Find x.

Answer

Let AD be the altitude. In isosceles triangle, the altitude to base bisects the base.

∴ BD = CD = 5 cm.

From figure,

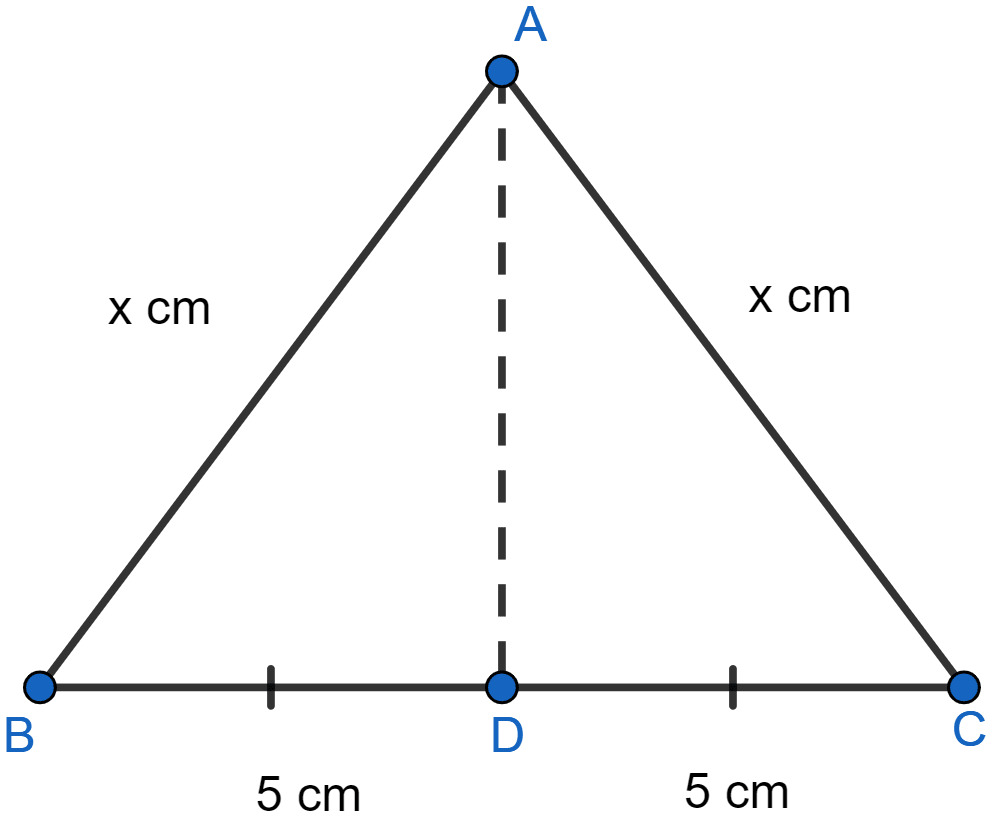
In right triangle ABD,

AB² = AD² + BD²

x² = AD² + 5²

AD² = x² - 25.

AD = $\sqrt{x^2 - 25}$

$\text{Area of △ABC } = \dfrac{1}{2} \times \text{AD} \times \text{BC} \\[1em] \Rightarrow 60 = \dfrac{1}{2} \times \sqrt{x^2 - 25} \times 10 \\[1em] \Rightarrow 120 = 10\sqrt{x^2 - 25} \\[1em] \Rightarrow \sqrt{x^2 - 25} = 12 \\[1em] \Rightarrow x^2 - 25 = 144 \\[1em] \Rightarrow x^2 = 169 \\[1em] \Rightarrow x = \sqrt{169} = 13.$

Hence, x = 13 cm.

In rhombus if diagonals are 30 cm and 40 cm, find its perimeter.

Answer

Let AC = 30 cm and BD = 40 cm.

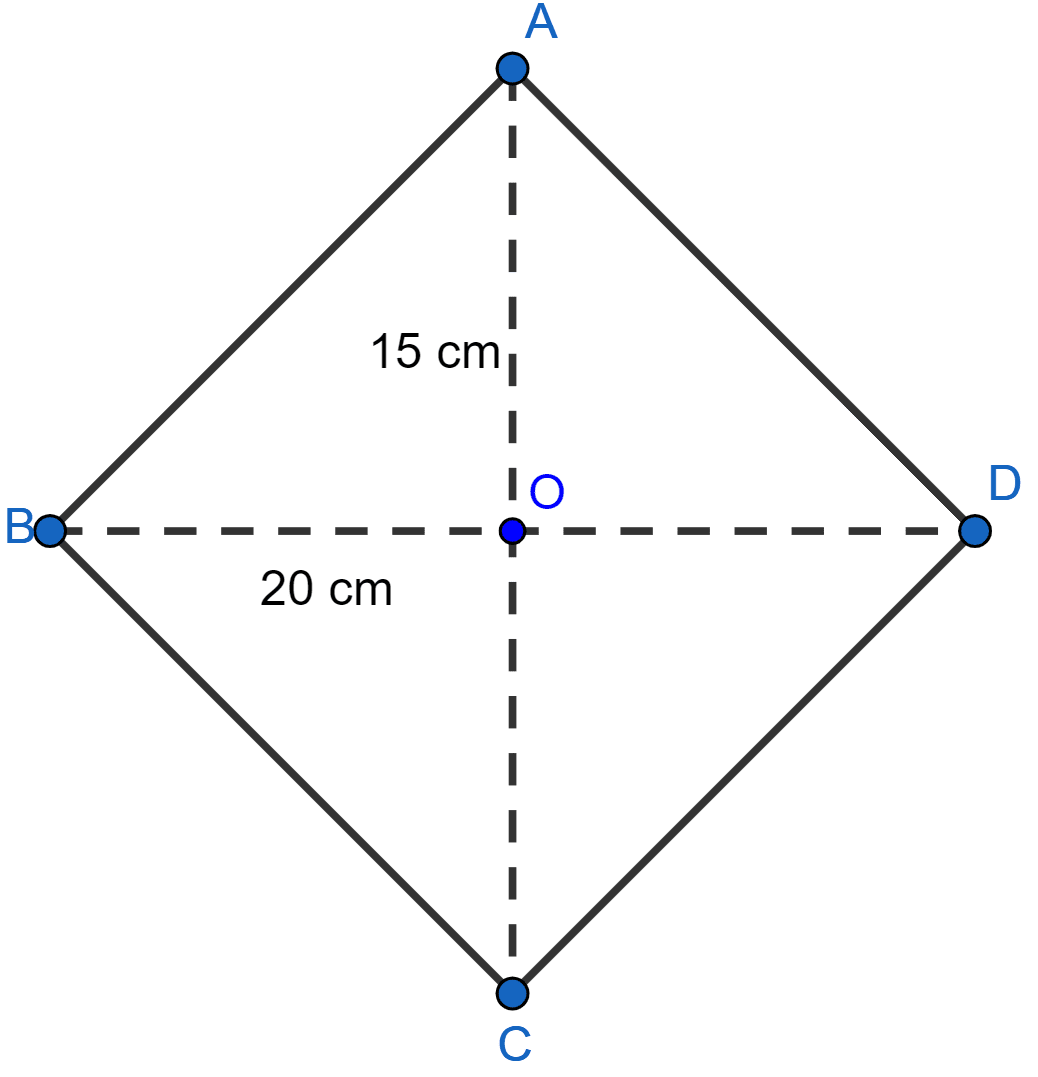
We know that,

Diagonals of rhombus are perpendicular and bisect each other,

OB = $\dfrac{1}{2}BD$ = 20 cm and AO = $\dfrac{1}{2}$AC = 15 cm.

In right triangle AOB,

By pythagoras theorem we get,

⇒ AB² = AO² + OB²

⇒ AB² = 15² + 20²

⇒ AB² = 225 + 400

⇒ AB² = 625

⇒ AB = 25 cm.

Hence, each side of rhombus is 25 cm as all sides of rhombus are equal.

Perimeter = 4(Side) = 100 cm.

Hence, perimeter of rhombus = 100 cm.

In figure given below, AB || DC, BC = AD = 13 cm, AB = 22 cm and DC = 12 cm. Calculate the height of the trapezium ABCD.

Answer

From figure,

EF = DC = 12 cm

Since,

AD = BC and DE = CF = h (height)

∴ AE = FB = x.

⇒ AB = AE + EF + FB

⇒ 22 = x + 12 + x

⇒ 2x = 22 - 12

⇒ 2x = 10

⇒ x = 5 cm.

In right triangle ADE,

By pythagoras theorem,

⇒ AD² = DE² + AE²

⇒ 13² = h² + 5²

⇒ 169 - 25 = h²

⇒ h² = 144

⇒ h = 12 cm.

Hence, height = 12 cm.

In figure given below, AB || DC, ∠A = 90°, DC = 7 cm, AB = 17 cm and AC = 25 cm. Calculate BC.

Answer

Since, AB || DC

∠D = ∠A = 90°

In right angle triangle ACD,

By pythagoras theorem,

⇒ AC² = AD² + CD²

⇒ 25² = AD² + 7²

⇒ 625 = AD² + 49

⇒ AD² = 625 - 49

⇒ AD² = 576

⇒ AD = $\sqrt{576}$ = 24 cm.

From figure,

CE = AD = 24 cm

In right angle triangle ACE,

By pythagoras theorem,

⇒ AC² = AE² + CE²

⇒ 25² = AE² + 24²

⇒ 625 = AE² + 576

⇒ AE² = 625 - 576

⇒ AE² = 49

⇒ AE = $\sqrt{49}$ = 7 cm.

So, EB = AB - AE = 17 - 7 = 10 cm.

In right angle triangle BCE,

By pythagoras theorem,

⇒ BC² = CE² + EB²

⇒ BC² = 24² + 10²

⇒ BC² = 576 + 100

⇒ BC² = 676

⇒ BC = $\sqrt{676}$ = 26 cm.

Hence, BC = 26 cm.

In the figure given below, ABCD is a square of side 7 cm. If

AE = FC = CG = HA = 3 cm,

(i) prove that EFGH is a rectangle.

(ii) find the area and perimeter of EFGH.

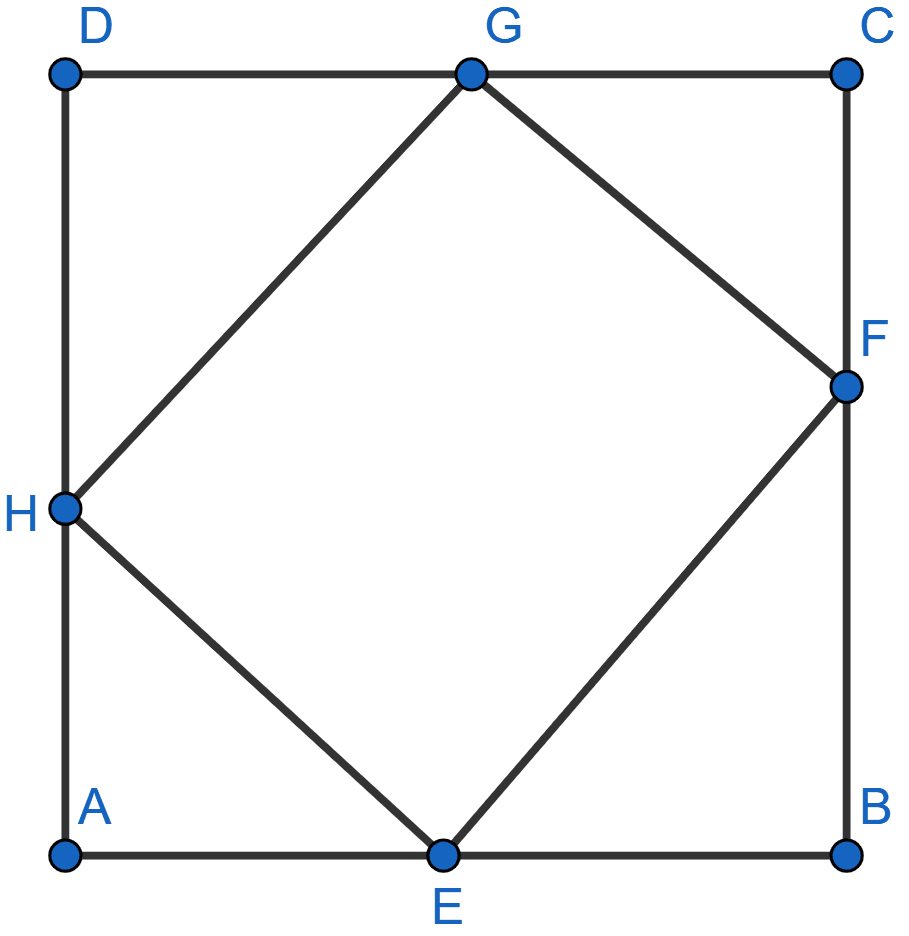
Answer

(i) Given, ABCD is a square of side 7 cm and AE = FC = CG = HA = 3 cm.

From figure,

DH = DA - HA = 7 - 3 = 4 cm,

GD = DC - CG = 7 - 3 = 4 cm,

EB = AB - AE = 7 - 3 = 4 cm,

FB = BC - FC = 7 - 3 = 4 cm.

Since in square, sides are perpendicular to each other,

By pythagoras theorem,

In right angle triangle HAE,

⇒ HE² = HA² + AE²

⇒ HE² = 3² + 3²

⇒ HE² = 9 + 9

⇒ HE² = 18

⇒ HE = $\sqrt{18} = 3\sqrt{2}$ cm.

In right angle triangle FCG,

⇒ GF² = GC² + FC²

⇒ GF² = 3² + 3²

⇒ GF² = 9 + 9

⇒ GF² = 18

⇒ GF = $\sqrt{18} = 3\sqrt{2}$ cm.

In right angle triangle GDH,

⇒ GH² = GD² + DH²

⇒ GH² = 4² + 4²

⇒ GH² = 16 + 16

⇒ GH² = 32

⇒ GH = $\sqrt{32} = 4\sqrt{2}$ cm.

In right angle triangle EBF,

⇒ EF² = EB² + FB²

⇒ EF² = 4² + 4²

⇒ EF² = 16 + 16

⇒ EF² = 32

⇒ EF = $\sqrt{32} = 4\sqrt{2}$ cm.

In isosceles triangle AEH,

∠E = ∠H = x (let) (As angles opposite to equal side in isosceles triangle are equal).

So, ∠A + ∠E + ∠H = 180°

90° + x + x = 180°

2x = 90°

x = 45°

Similar is the case for triangles EBF, GDH, FCG.

From figure,

∠AEH + ∠HEF + ∠FEB = 180° (Linear pairs)

45° + ∠HEF + 45° = 180°

∠HEF = 90°

Since, angles of EFGH = 90° and EH = GF and HG = EF.

Hence, proved that EFGH is a rectangle.

(ii) Area of EFGH = EF × GF = $4\sqrt{2} \times 3\sqrt{2}$ = 24 cm².

Perimeter of EFGH = 2(EF + GF) = $2(4\sqrt{2} + 3\sqrt{2}) = 14\sqrt{2}$ cm.

Hence, area = 24 cm² and perimeter = $14\sqrt{2}$ cm.

AD is perpendicular to the side BC of an equilateral △ABC. Prove that 4AD² = 3AB².

Answer

Given, AD ⊥ BC and AB = BC = CA (Equilateral triangle).

The perpendicular to base in equilateral triangle bisects the base.

∴ BD = $\dfrac{BC}{2}$.

From figure,

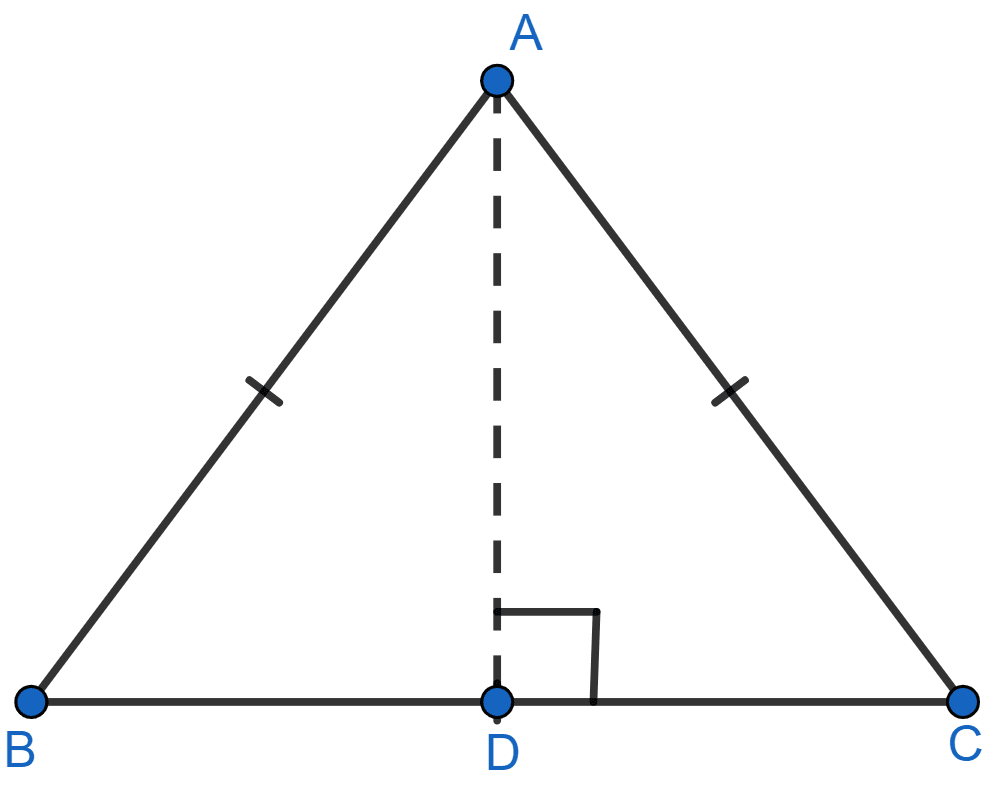
In right triangle ABD,

By pythagoras theorem,

⇒ AB² = AD² + BD²

⇒ AB² = AD² + $\Big(\dfrac{BC}{2}\Big)^2$

⇒ AB² = AD² + $\dfrac{BC^2}{4}$

⇒ AB² = $\dfrac{4\text{AD}^2 + \text{BC}^2}{4}$

⇒ 4AB² = 4AD² + BC²

⇒ 4AB² = 4AD² + AB² (∵ BC = AB)

⇒ 4AD² = 3AB².

Hence, proved that 4AD² = 3AB².

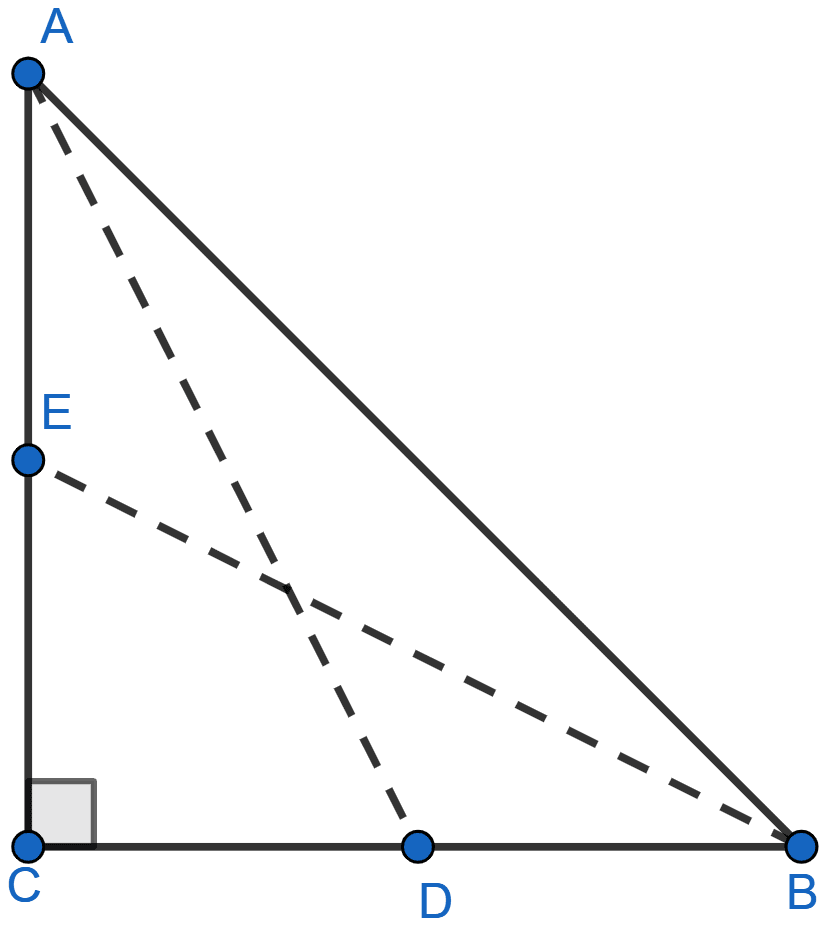
In the adjoining figure, D and E are mid-points of the sides BC and CA respectively of a △ABC, right angled at C. Prove that :

(i) 4AD² = 4AC² + BC²

(ii) 4BE² = 4BC² + AC²

(iii) 4(AD² + BE²) = 5AB²

Answer

(i) Since, D is mid-point of BC,

∴ CD = $\dfrac{BC}{2}$

In right triangle ACD,

By pythagoras theorem,

⇒ AD² = AC² + CD²

⇒ AD² = AC² + $\Big(\dfrac{BC}{2}\Big)^2$

⇒ AD² = AC² + $\dfrac{BC^2}{4}$

⇒ AD² = $\dfrac{4\text{AC}^2 + \text{BC}^2}{4}$

⇒ 4AD² = 4AC² + BC² .....(1)

Hence, proved that 4AD² = 4AC² + BC².

(ii) As E is mid-point of AC,

∴ CE = $\dfrac{AC}{2}$

⇒ AC = 2CE

BCE is right triangle,

By pythagoras theorem,

⇒ BE² = BC² + CE²

Multiplying both sides by 4 we get,

⇒ 4BE² = 4BC² + 4CE²

⇒ 4BE² = 4BC² + (2CE)²

⇒ 4BE² = 4BC² + AC² ......(2)

Hence, proved that 4BE² = 4BC² + AC².

(iii) As, ABC is a right triangle,

By pythagoras theorem we get,

⇒ AB² = AC² + BC²

Adding 1 and 2 from above parts we get,

⇒ 4AD² + 4BE² = 4AC² + BC² + 4BC² + AC²

⇒ 4(AD² + BE²) = 5AC² + 5BC²

⇒ 4(AD² + BE²) = 5(AC² + BC²)

⇒ 4(AD² + BE²) = 5AB².

Hence, proved that 4(AD² + BE²) = 5AB².

If AD, BE and CF are medians of △ABC, prove that

3(AB² + BC² + CA²) = 4(AD² + BE² + CF²).

Answer

Draw AP perpendicular to BC.

In right triangle APD,

By pythagoras theorem,

AD² = AP² + PD² .......(i)

In right triangle APB,

By pythagoras theorem,

⇒ AB² = AP² + BP²

⇒ AB² = AP² + (BD - PD)²

⇒ AB² = AP² + BD² + PD² - 2BD.PD

Since, BD = $\dfrac{\text{BC}}{2}$ as AD is median of BC.

⇒ AB² = AP² + PD² + $\Big(\dfrac{\text{BC}}{2}\Big)^2$ - 2 x $\dfrac{\text{BC}}{2}$ x PD

⇒ AB² = AD² + $\dfrac{\text{BC}^2}{4}$ - BC.PD ....(ii) (From i)

In right triangle APC,

By pythagoras theorem,

⇒ AC² = AP² + PC²

⇒ AC² = AP² + (PD + DC)²

⇒ AC² = AP² + PD² + DC² + 2PD.DC

Since, DC = $\dfrac{BC}{2}$

⇒ AC² = AD² + DC² + 2PD.DC [....From (i)]

⇒ AC² = AD² + $\Big(\dfrac{\text{BC}}{2}\Big)^2$ + 2 x PD x $\dfrac{\text{BC}}{2}$

⇒ AC² = AD² + $\dfrac{\text{BC}^2}{4}$ + PD.BC ....(iii)

Adding (ii) and (iii) we get,

⇒ AB² + AC² = AD² + $\dfrac{\text{BC}^2}{4}$ - BC.PD + AD² + $\dfrac{\text{BC}^2}{4}$ + PD.BC

⇒ AB² + AC² = 2AD² + $\dfrac{\text{BC}^2}{2}$ ....(iv)

Draw BQ perpendicular to AC,

In right triangle BQE,

By pythagoras theorem,

BE² = BQ² + QE² .......(v)

In right triangle ABQ,

By pythagoras theorem,

⇒ AB² = BQ² + AQ²

⇒ AB² = BQ² + (AE - QE)²

⇒ AB² = BQ² + QE² + AE² - 2AE.QE

Since, AE = $\dfrac{\text{AC}}{2}$ as BE is median of AC.

⇒ AB² = BE² + $\Big(\dfrac{\text{AC}}{2}\Big)^2$ - 2 x $\dfrac{\text{AC}}{2}$ x QE (From v)

⇒ AB² = BE² + $\dfrac{\text{AC}^2}{4}$ - AC.QE ....(vi)

In right triangle BQC,

By pythagoras theorem,

⇒ BC² = BQ² + QC²

⇒ BC² = BQ² + (QE + EC)²

⇒ BC² = BQ² + QE² + EC² + 2QE.EC

Since, EC = $\dfrac{AC}{2}$ as BE is median of AC.

⇒ BC² = BE² + EC² + 2QE.EC [....From (v)]

⇒ BC² = BE² + $\Big(\dfrac{\text{AC}}{2}\Big)^2$ + 2 x QE x $\dfrac{\text{AC}}{2}$

⇒ BC² = BE² + $\dfrac{\text{AC}^2}{4}$ + QE.AC ....(vii)

Adding (vi) and (vii) we get,

⇒ AB² + BC² = BE² + $\dfrac{\text{AC}^2}{4}$ - AC.QE + BE² + $\dfrac{\text{AC}^2}{4}$ + QE.AC

⇒ AB² + BC² = 2BE² + $\dfrac{\text{AC}^2}{2}$ ....(viii)

Draw CR perpendicular to AB,

In right triangle CFR,

By pythagoras theorem,

CF² = CR² + FR² .......(ix)

In right triangle CBR,

By pythagoras theorem,

⇒ CB² = CR² + RB²

⇒ CB² = CR² + (BF - FR)²

⇒ CB² = CR² + FR² + BF² - 2BF.FR

Since, BF = $\dfrac{\text{AB}}{2}$ as CF is median of AB.

⇒ CB² = CF² + $\Big(\dfrac{\text{AB}}{2}\Big)^2$ - 2 x $\dfrac{\text{AB}}{2}$ x FR (From ix)

⇒ CB² = CF² + $\dfrac{\text{AB}^2}{4}$ - AB.FR ....(x)

In right triangle ACR,

By pythagoras theorem,

⇒ AC² = RC² + AR²

⇒ AC² = RC² + (AF + FR)²

⇒ AC² = RC² + FR² + AF² + 2AF.FR

Since, AF = $\dfrac{\text{AB}}{2}$ as CF is median of AB.

⇒ AC² = CF² + AF² + 2AF.FR [....From (ix)]

⇒ AC² = CF² + $\Big(\dfrac{\text{AB}}{2}\Big)^2$ + 2 x FR x $\dfrac{\text{AB}}{2}$

⇒ AC² = CF² + $\dfrac{\text{AB}^2}{4}$ + FR.AB ....(xi)

Adding (x) and (xi) we get,

⇒ CB² + AC² = CF² + $\dfrac{\text{AB}^2}{4}$ - AB.FR + CF² + $\dfrac{\text{AB}^2}{4}$ + FR.AB

⇒ CB² + AC² = 2CF² + $\dfrac{\text{AB}^2}{2}$ ....(xii)

On adding (iv), (viii) and (xii) we get,

AB² + AC² + AB² + BC² + CB² + AC² = 2AD² + $\dfrac{\text{BC}^2}{2}$ + 2BE² + $\dfrac{\text{AC}^2}{2}$ + 2CF² + $\dfrac{\text{AB}^2}{2}$

⇒ 2(AB² + BC² + CA²) = 2(AD² + BE² + CF²) + $\dfrac{1}{2}$(AB² + BC² + CA²)

⇒ 2(AB² + BC² + CA²) - $\dfrac{1}{2}$(AB² + BC² + CA²) = 2(AD² + BE² + CF²)

⇒ $\dfrac{3}{2}$(AB² + BC² + CA²) = 2(AD² + BE² + CF²)

⇒ $3$(AB² + BC² + CA²) = 4(AD² + BE² + CF²)

Hence, proved that 3(AB² + BC² + CA²) = 4(AD² + BE² + CF²).

In the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O, at right angles. Prove that AB² + CD² = AD² + BC².

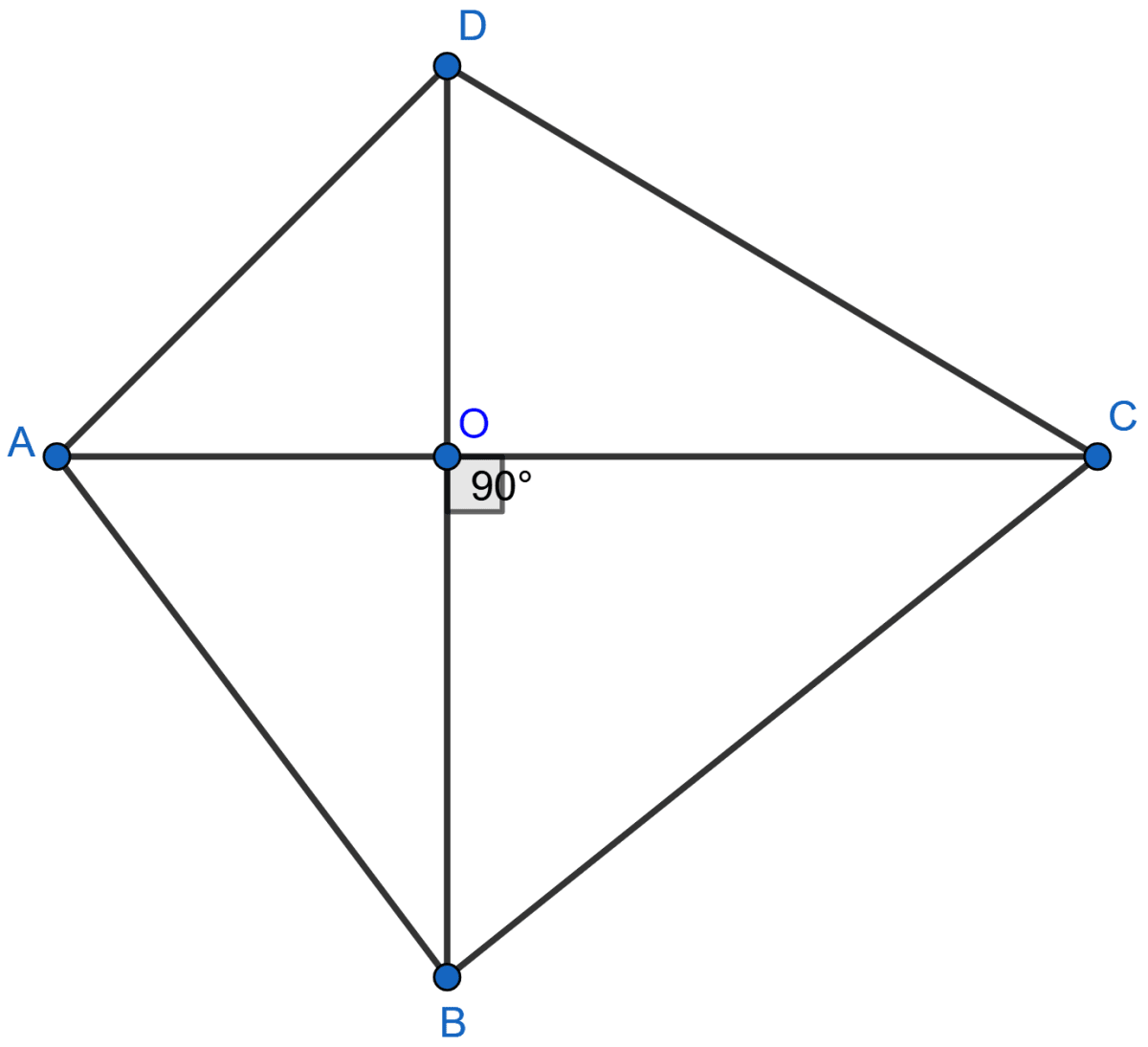
Answer

By pythagoras theorem,

In right angle triangle AOB,

AB² = OB² + OA² .......(i)

In right angle triangle COD,

CD² = OC² + OD² .......(ii)

In right angle triangle AOD,

AD² = AO² + OD² .......(iii)

In right angle triangle BOC,

BC² = OB² + OC² .......(iv)

Adding (i), (ii) we get,

AB² + CD² = OB² + OA² + OC² + OD²

AB² + CD² = (OA² + OD²) + (OC² + OB²)

Substituting value from (iii) and (iv) in above equation we get,

AB² + CD² = AD² + BC².

Hence, proved that AB² + CD² = AD² + BC².

In a quadrilateral ABCD, ∠B = 90° = ∠D. Prove that

2AC² - BC² = AB² + AD² + DC².

Answer

Given, ∠B = 90° = ∠D

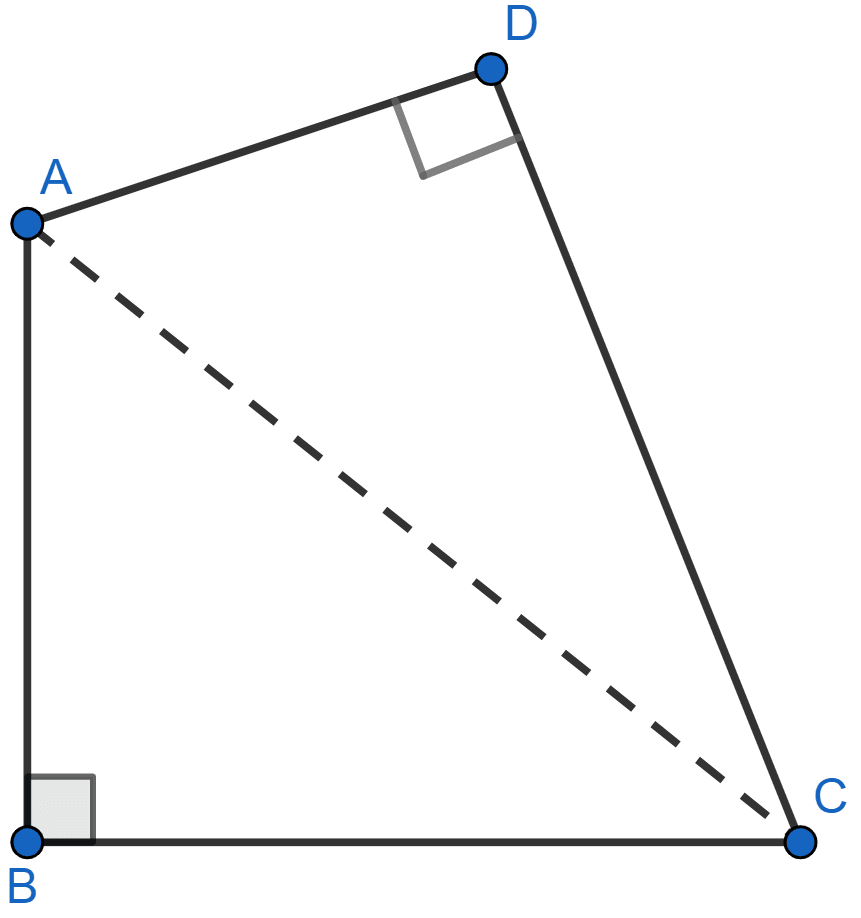
By pythagoras theorem,

In right angle triangle ABC,

AC² = AB² + BC² ......(i)

By pythagoras theorem,

In right angle triangle ADC,

AC² = AD² + DC² ......(ii)

Adding (i) and (ii) we get,

2AC² = AB² + BC² + AD² + DC²

2AC² - BC² = AB² + AD² + DC².

Hence, proved that 2AC² - BC² = AB² + AD² + DC².

In a △ABC, ∠A = 90°, CA = AB and D is a point on AB produced. Prove that

DC² - BD² = 2AB × AD.

Answer

In right angle triangle ACD,

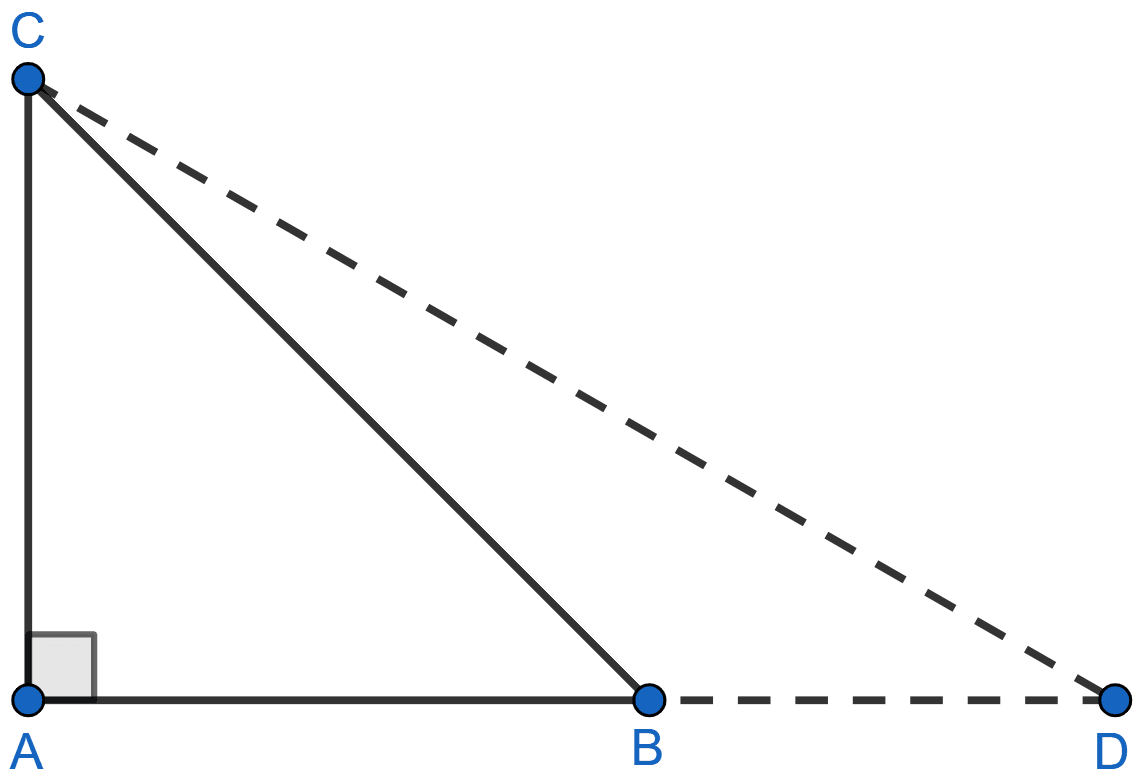
DC² = CA² + AD² (Pythagoras theorem)

DC² = CA² + (AB + BD)²

DC² = CA² + AB² + BD² + 2AB.BD

DC² - BD² = AB² + AB² + 2AB.BD [∵ CA = AB]

DC² - BD² = 2AB² + 2AB.BD

DC² - BD² = 2AB(AB + BD)

From figure, AB + BD = AD

DC² - BD² = 2AB.AD

Hence, proved that DC² - BD² = 2AB.AD.

In an isosceles triangle ABC, AB = AC and D is a point on BC produced. Prove that AD² = AC² + BD × CD.

Answer

Draw AP ⊥ BC.

APD is right triangle

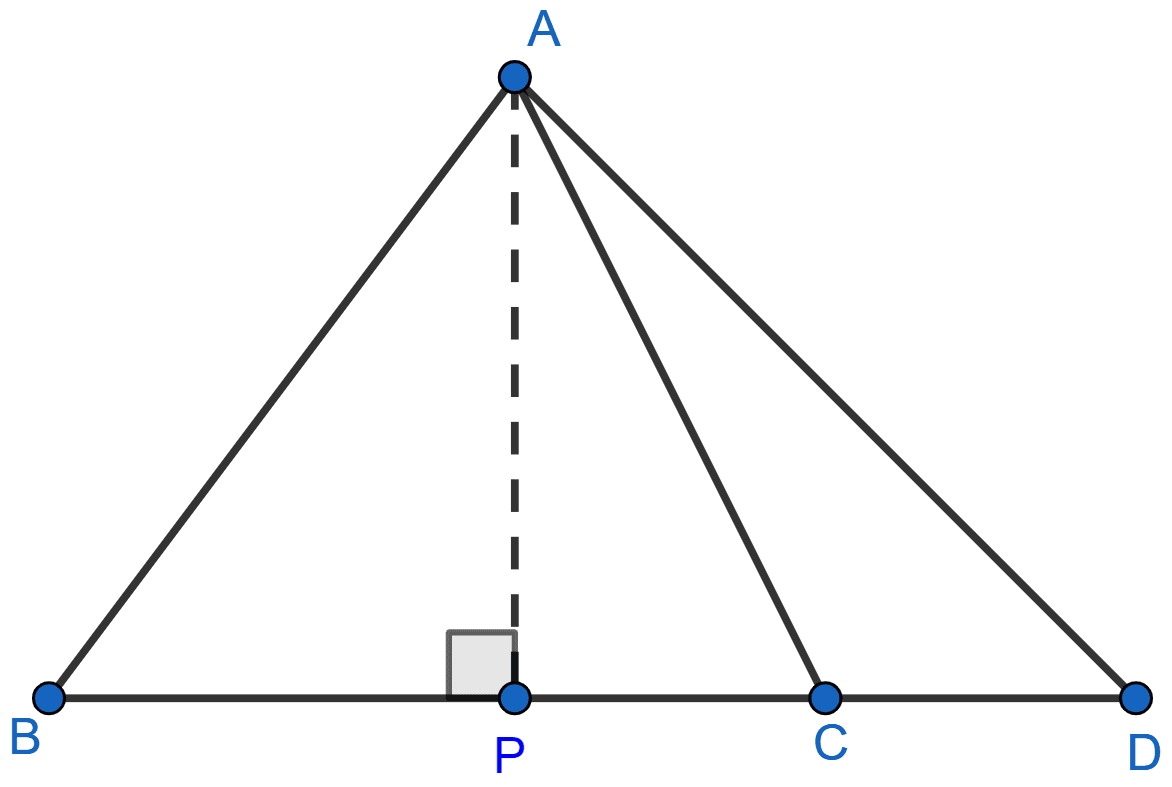
By pythagoras theorem we get,

⇒ AD² = AP² + PD²

⇒ AD² = AP² + (PC + CD)²

⇒ AD² = AP² + PC² + CD² + 2PC.CD ......(i)

APC is right triangle,

By pythagoras theorem we get,

⇒ AC² = AP² + PC² ......(ii)

Substituting the value of AP² + PC² from (ii) in (i) we get,

⇒ AD² = AC² + CD² + 2PC.CD .......(iii)

Since, ABC is an isosceles triangle,

⇒ PC = $\dfrac{\text{BC}}{2}$ [∵ altitude to the base of an isosceles triangle bisects the base]

⇒ AD² = AC² + CD² + $2 \times \dfrac{1}{2} \times \text{BC} \times \text{CD}$

⇒ AD² = AC² + CD² + BC.CD

⇒ AD² = AC² + CD(CD + BC)

From figure, CD + BC = BD

⇒ AD² = AC² + CD.BD

Hence, proved that AD² = AC² + BD × CD.

In a △ABC, if AB = $6\sqrt{3}$ cm, BC = 6 cm and AC = 12 cm, then ∠B is

1. 120°

2. 90°

3. 60°

4. 45°

Answer

Here greatest length is 12 cm and other lengths are 6 cm, $6\sqrt{3}$ cm.

Note that 12² = 144 and 6² + $(6\sqrt{3})^2$ = 36 + 108 = 144.

Thus, 12² = 6² + $(6\sqrt{3})^2$.

Hence, ABC is right triangle with hypotenuse = AC = 12 cm.

So, angle opposite to AC i.e. ∠B = 90°.

Hence, Option 2 is the correct option.

If the sides of a rectangular plot are 15 m and 8 m, then the length of its diagonal is

1. 17 m

2. 23 m

3. 21 m

4. 17 cm

Answer

As sides of rectangle are perpendicular to each other so △ABC is a right angle triangle.

In right angle triangle ABC,

⇒ AC² = AB² + BC²

⇒ AC² = 8² + 15²

⇒ AC² = 64 + 225

⇒ AC² = 289

⇒ AC = $\sqrt{289}$ = 17 m.

Hence, Option 1 is the correct option.

The lengths of the diagonals of a rhombus are 16 cm and 12 cm. The length of the side of rhombus is

1. 9 cm

2. 10 cm

3. 8 cm

4. 20 cm

Answer

Let AC = 16 cm and BD = 12 cm.

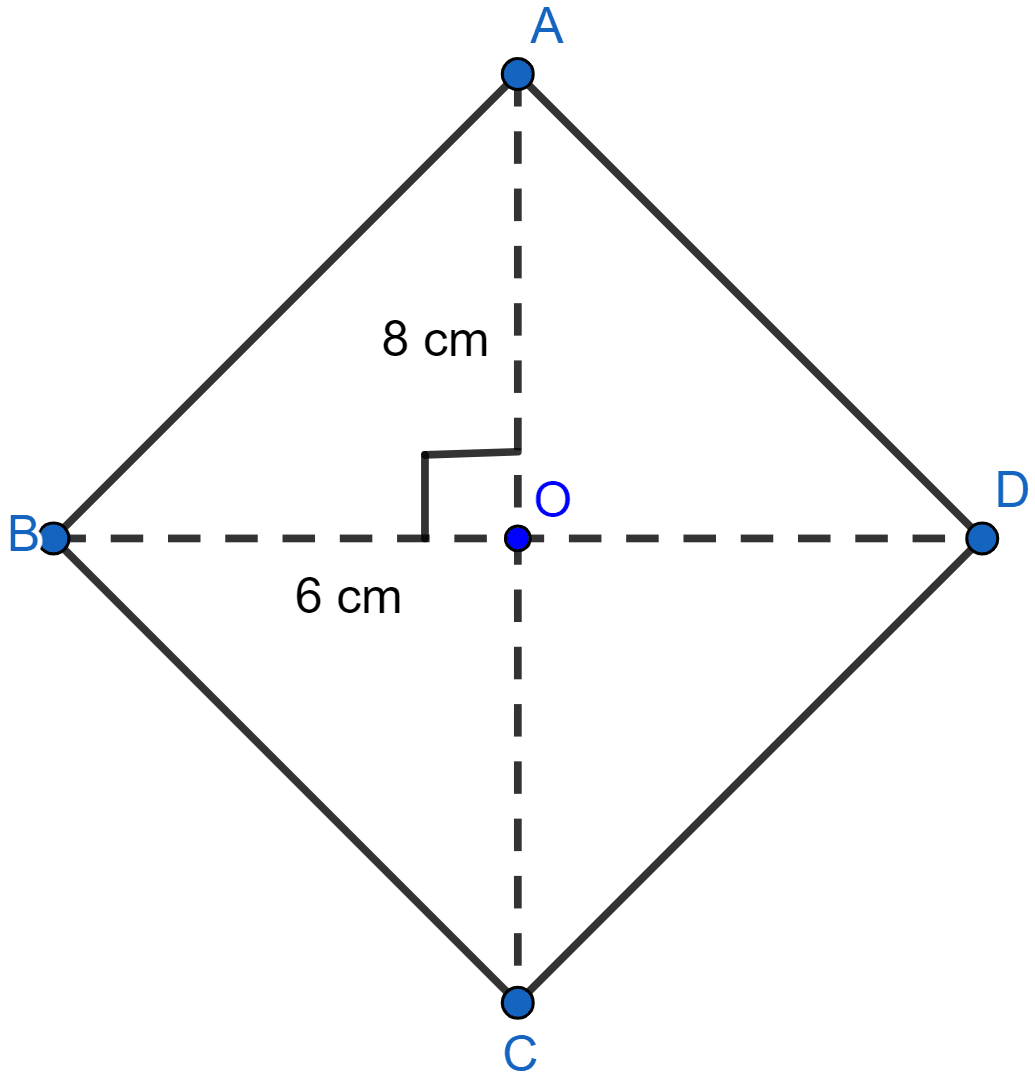
We know that,

Diagonals of rhombus are perpendicular and bisect each other,

OB = $\dfrac{1}{2}BD$ = 6 cm and AO = $\dfrac{1}{2}$AC = 8 cm.

In right triangle AOB,

By pythagoras theorem we get,

⇒ AB² = AO² + OB²

⇒ AB² = 8² + 6²

⇒ AB² = 64 + 36

⇒ AB² = 100

⇒ AB = $\sqrt{100}$ = 10 cm.

Hence, Option 2 is the correct option.

If a side of a rhombus is 10 cm and one of the diagonals is 16 cm, then the length of the other diagonal is

1. 6 cm

2. 12 cm

3. 20 cm

4. 12 cm

Answer

Let AC = 16 cm.

We know that,

Diagonals of rhombus are perpendicular and bisect each other,

AO = $\dfrac{1}{2}$AC = 8 cm.

In right triangle AOB,

By pythagoras theorem we get,

⇒ AB² = AO² + OB²

⇒ 10² = 8² + OB²

⇒ 100 = 64 + OB²

⇒ OB² = 100 - 64 = 36

⇒ OB = $\sqrt{36}$ = 6 cm.

BD = 2OB = 12 cm.

Hence, Option 2 is the correct option.

If a ladder 10 m long reaches a window 8 m above the ground, then the distance of the foot of the ladder from the base of the wall is

1. 18 m

2. 8 m

3. 6 m

4. 4 m

Answer

Let AB be the ladder and B be the point of window.

In right triangle ACB,

By pythagoras theorem,

⇒ AB² = AC² + BC²

⇒ 10² = AC² + 8²

⇒ AC² = 100 - 64

⇒ AC² = 36

⇒ AC = $\sqrt{36}$ = 6 m.

Hence, Option 3 is the correct option.

A girl walks 200 m towards East and then she walks 150 m towards North. The distance of the girl from starting point is

1. 350 m

2. 250 m

3. 300 m

4. 225 m

Answer

Let A be starting point and B is the end point.

In right triangle ACB,

By pythagoras theorem we get,

AB² = AC² + CB²

AB² = (200)² + (150)²

AB² = 40000 + 22500

AB² = 62500

AB = $\sqrt{62500}$ = 250 m.

Hence, Option 2 is the correct option.

A ladder reaches a window 12 m above the ground on one side of the street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 9 m high. If the length of the ladder is 15 m, then the width of the street is

1. 30 m

2. 24 m

3. 21 m

4. 18 m

Answer

In right triangle AEB,

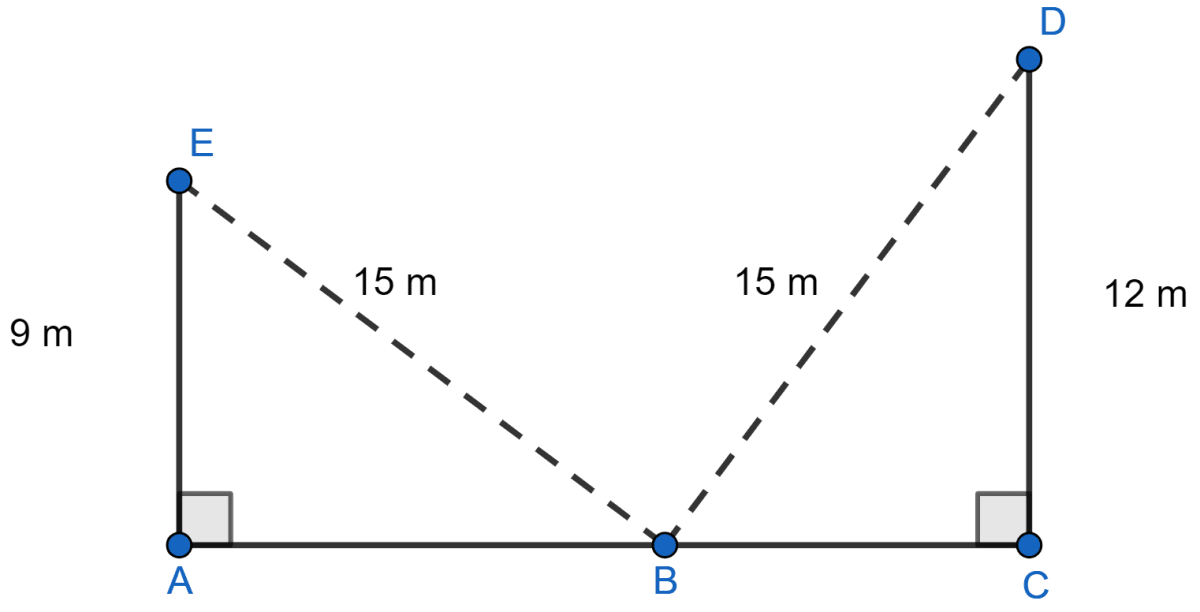
By pythagoras theorem we get,

⇒ EB² = EA² + AB²

⇒ 15² = 9² + AB²

⇒ 225 = 81 + AB²

⇒ AB² = 144

⇒ AB = $\sqrt{144}$ = 12 m

In right triangle BCD,

By pythagoras theorem we get,

⇒ BD² = BC² + CD²

⇒ 15² = BC² + 12²

⇒ 225 = BC² + 144

⇒ 225 - 144 = BC²

⇒ BC² = 81

⇒ BC = $\sqrt{81}$ = 9 m

⇒ AC = AB + BC = 12 + 9 = 21 m.

Hence, Option 3 is the correct option.

Consider the following two statements:

Statement 1: The area of a square whose diagonal is 6 cm is 36 cm².

Statement 2: A diagonal of a square divides it into two right angled isosceles triangle.

Which of the following is valid?

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and Statement 2 is false.

4. Statement 1 is false, and Statement 2 is true.

Answer

Let's consider a square ABCD with diagonal AC.

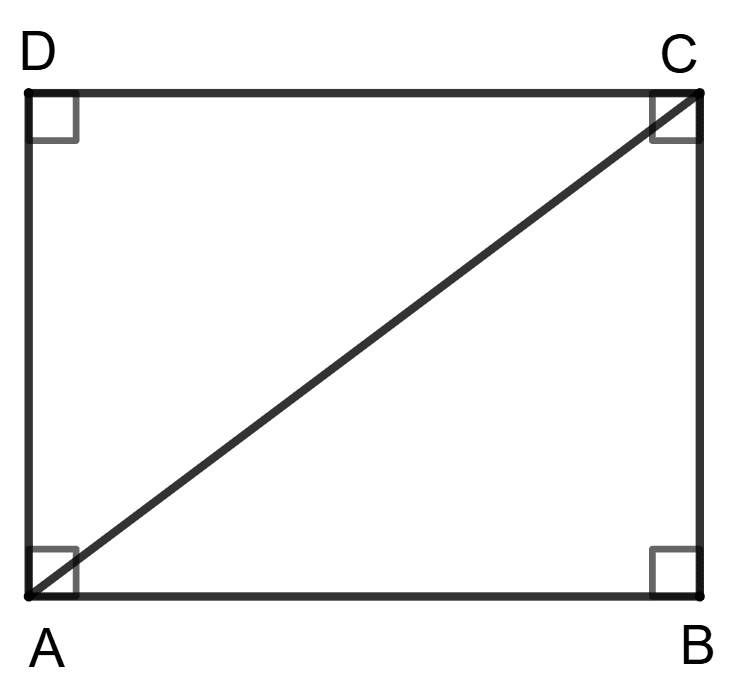
A square is a quadrilateral with four right angles.

Therefore, ∠A = ∠B = ∠C = ∠D = 90°.

AC divides the square into two triangles: △ABC and △ADC.

Both these triangles contain a right angle (at B and D respectively). Thus, they are right-angled triangles.

A square has all four sides equal in length. So, AB = BC = CD = DA.

In △ABC, the two sides AB and BC are equal (sides of the square).

In △ADC, the two sides AD and CD are equal (sides of the square).

Thus, AC divides the square into two right angled isosceles triangles.

∴ Statement 2 is true.

In triangle ABC,

By the Pythagorean theorem:

⇒ AC² = AB² + BC²

Let length of each side of square be a cm and length of diagonal equal to 6 cm (given).

⇒ 6² = a² + a²

⇒ 36 = 2a²

⇒ a² = $\dfrac{36}{2}$ = 18 cm²

As we know that area of square = a²

Thus, area = 18 cm².

∴ Statement 1 is false.

∴ Statement 1 is false, and Statement 2 is true.

Hence, option 4 is the correct option.

Assertion (A): If the sides of a rectangular plot are 80 m and 60 m, then the length of its diagonal is 100 m.

Reason (R): In a rectangle, all angles are 90°.

1. Assertion (A) is true, Reason (R) is false.

2. Assertion (A) is false, Reason (R) is true.

3. Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).

4. Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).

Answer

A rectangle is a quadrilateral with four right angles.

Let ABCD be the rectangular plot.

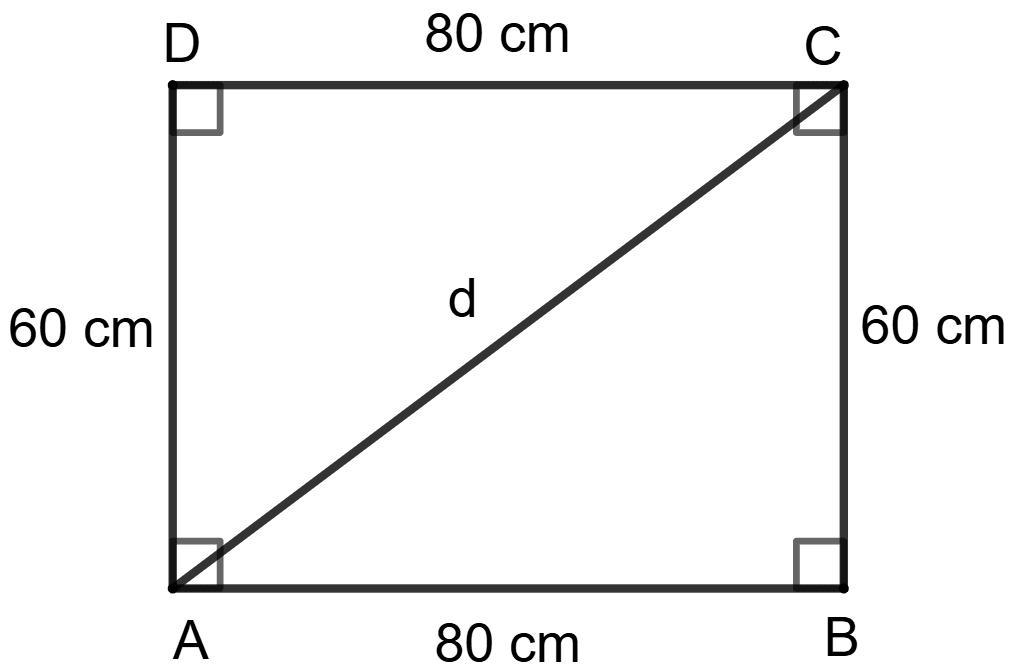
Thus, in a rectangle, all angles are 90°.

∴ Reason (R) is true.

Given:

Side 1 (AB) = 80 m

Side 2 (BC) = 60 m

Let d be the length of the diagonal (AC). Using pythagoras theorem in triangle ABC,

⇒ AC² = AB² + BC²

⇒ d² = 80² + 60²

⇒ d² = 6400 + 3600

⇒ d² = 10000

⇒ d = $\sqrt{10000}$

⇒ d = ± 100 m

Since, length cannot be negative, so, diagonal = 100 m.

∴ Assertion (A) is true.

∴ Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason (or explanation) for Assertion (A).

Hence, option 3 is the correct option.

Assertion (A): If triangle ABC is isosceles with AC = BC and AB² = 2AC², then triangle ABC is right angled.

Reason (R): If in a triangle ABC, we have AB² = 2AC² then we can conclude that it is right angled triangle.

1. Assertion (A) is true, Reason (R) is false.

2. Assertion (A) is false, Reason (R) is true.

3. Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).

4. Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).

Answer

Given, triangle ABC is isosceles with AC = BC and, AB² = 2AC²

⇒ AB² = AC² + AC²

⇒ AB² = AC² + BC²

This equation AB² = AC² + BC² is the form of the Pythagorean Theorem where AB is the hypotenuse and AC and BC are the other sides of te triangle.

Since, pythagoras theorem is satisfied, thus ABC is a right angle triangle.

∴ Assertion (A) is true.

Alone with the relation, AB² = 2AC², we cannot conclude that it is right angled triangle because there is no mention of the third side BC.

∴ Reason (R) is false.

∴ Assertion (A) is true, Reason (R) is false.

Hence, option 1 is the correct option.

Assertion (A): A triangle with sides 2 cm, 3 cm, 4 cm is not a right angled triangle.

Reason (R): A triangle with sides 2 cm, 3 cm, 4 cm is a scalene triangle.

1. Assertion (A) is true, Reason (R) is false.

2. Assertion (A) is false, Reason (R) is true.

3. Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).

4. Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).

Answer

Given the sides: a = 2 cm, b = 3 cm, c = 4 cm.

The longest side is c = 4 cm.

Let's check if c² = a² + b²

Taking L.H.S.,

c² = 4² = 16.

Taking R.H.S.,

a² + b² = 2² + 3²

= 4 + 9

= 13.

Since 16 ≠ 13, the condition for a right-angled triangle is not met.

Therefore, the triangle with sides 2 cm, 3 cm, 4 cm is not a right-angled triangle.

∴ Assertion (A) is true.

A scalene triangle is defined as a triangle in which all three sides have different lengths.

Given the side lengths are 2 cm, 3 cm, and 4 cm. All three lengths are distinct.

∴ Reason (R) is true.

∴ Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).

Hence, option 4 is the correct option.

In the figure given below, AD ⊥ BC, AB = 25 cm, AC = 17 cm and AD = 15 cm. Find the length of BC.

Answer

By pythagoras theorem,

In right angle triangle ADB,

⇒ AB² = AD² + BD²

⇒ 25² = 15² + BD²

⇒ 625 = 225 + BD²

⇒ BD² = 625 - 225 = 400

⇒ BD = $\sqrt{400}$ = 20 cm

In right angle triangle ADC,

⇒ AC² = AD² + DC²

⇒ 17² = 15² + DC²

⇒ 289 = 225 + DC²

⇒ DC² = 289 - 225 = 64

⇒ DC =$\sqrt{64}$ = 8 cm

From figure,

⇒ BC = BD + DC = 20 + 8 = 28 cm.

Hence, BC = 28 cm.

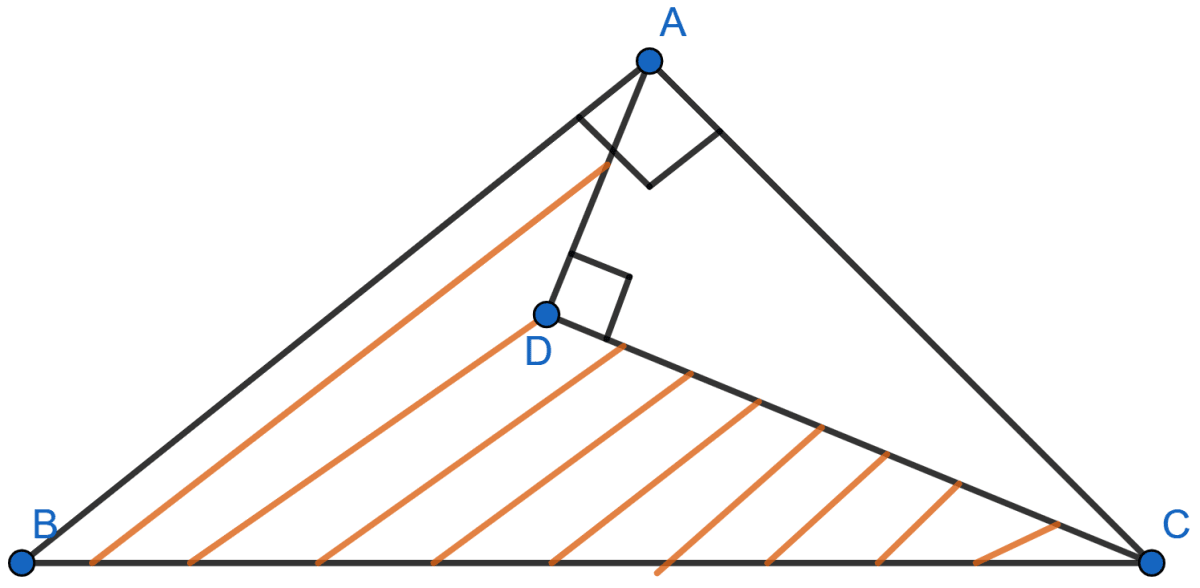
In the figure given below, ∠BAC = 90°, ADC = 90°, AD = 6 cm, CD = 8 cm and BC = 26 cm. Find

(i) AC

(ii) AB

(iii) area of the shaded region.

Answer

(i) By pythagoras theorem,

In right angle triangle ADC,

⇒ AC² = AD² + DC²

⇒ AC² = 6² + 8²

⇒ AC² = 36 + 64

⇒ AC² = 100

⇒ AC = $\sqrt{100}$ = 10 cm.

Hence, AC = 10 cm.

(ii) By pythagoras theorem,

In right angle triangle ABC,

⇒ BC² = AB² + AC²

⇒ 26² = AB² + 10²

⇒ AB² = 676 - 100

⇒ AB² = 576

⇒ AB = $\sqrt{576}$ = 24 cm.

Hence, AB = 24 cm.

(iii) Area of shaded region = Area of △ABC - Area of △ADC

$= \dfrac{1}{2} \times AB \times AC - \dfrac{1}{2} \times AD \times DC \\[1em] = \dfrac{1}{2} \times 24 \times 10 - \dfrac{1}{2} \times 6 \times 8 \\[1em] = 120 - 24 \\[1em] = 96 \text{ cm}^2.$

Hence, area of shaded region = 96 cm².

In figure given below, triangle ABC is right angled at B. Given that AB = 9 cm, AC = 15 cm and D, E are mid-points of the sides AB and AC respectively, calculate (i) the length of BC (ii) the area of △ADE.

Answer

(i) In right angle triangle ABC,

By pythagoras theorem,

⇒ AC² = AB² + BC²

⇒ 15² = 9² + BC²

⇒ BC² = 225 - 81

⇒ BC² = 144

⇒ BC = $\sqrt{144}$ = 12 cm.

Hence, BC = 12 cm.

(ii) Given, D and E are midpoints of AB and AC.

∴ By mid-point theorem,

DE = $\dfrac{1}{2}BC$ = 6 cm.

Area of △ADE = $\dfrac{1}{2} \times AD \times DE = \dfrac{1}{2} \times 4.5 \times 6$ = 13.5 cm²

Hence, area of △ADE = 13.5 cm².

If in △ABC, AB > AC and AD ⊥ BC, prove that AB² - AC² = BD² - CD².

Answer

From figure,

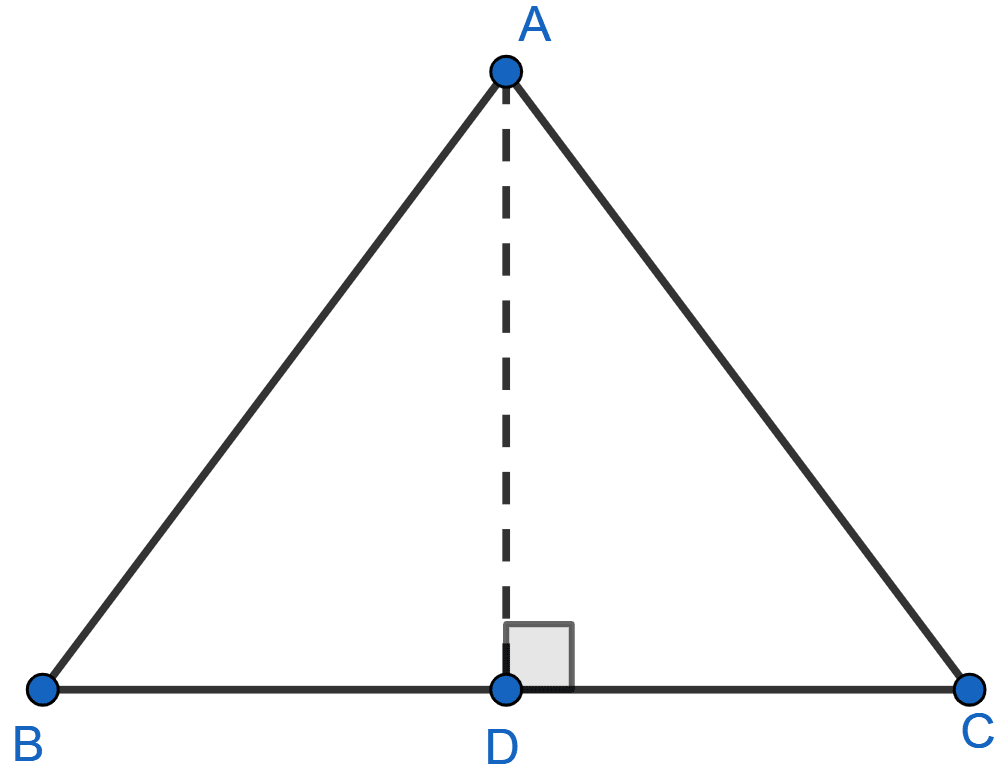
In right angle △ADB,

By pythagoras theorem we get,

AB² = AD² + BD² ........(i)

In right angle △ADC,

By pythagoras theorem we get,

AC² = AD² + CD² ........(ii)

Subtracting (ii) from (i),

AB² - AC² = AD² + BD² - (AD² + CD²)

AB² - AC² = BD² - CD².

Hence, proved that AB² - AC² = BD² - CD².

In a right angled triangle ABC, right angled at C, P and Q are the points on the sides CA and CB respectively which divide these sides in the ratio 2 : 1. Prove that

(i) 9AQ² = 9AC² + 4BC²

(ii) 9BP² = 9BC² + 4AC²

(iii) 9(AQ² + BP²) = 13AB²

Answer

(i) In right angle triangle ACQ,

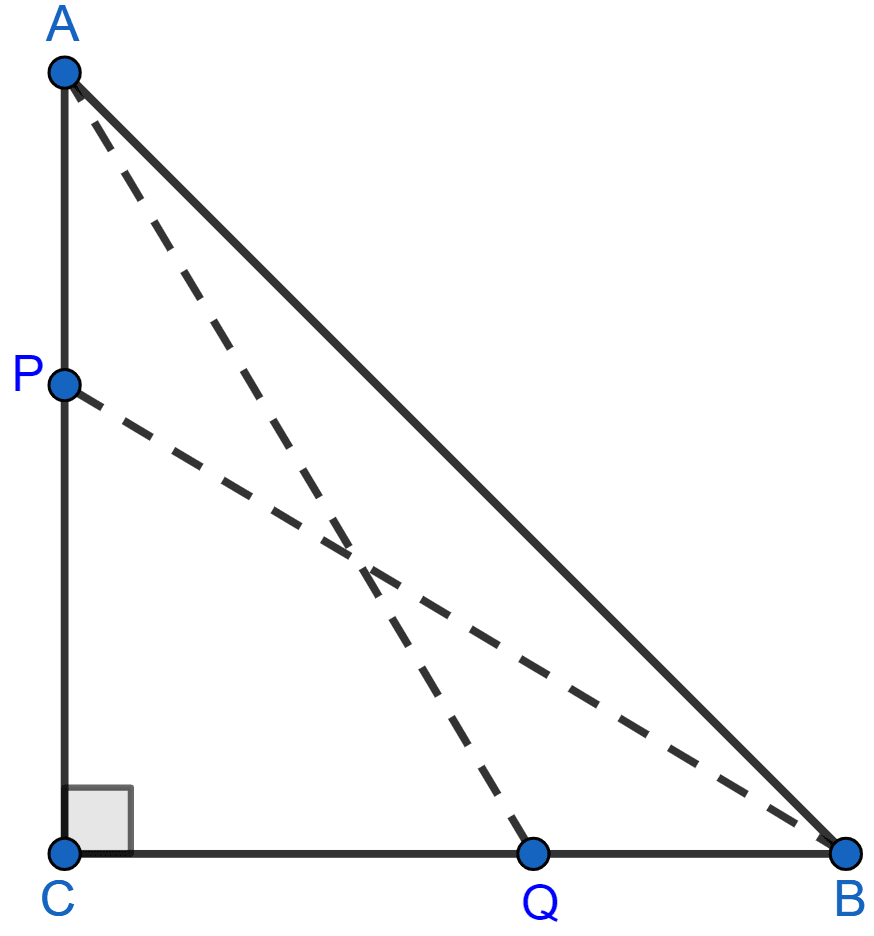
By pythagoras theorem we get,

⇒ AQ² = AC² + CQ²

Multiplying both sides by 9 we get,

⇒ 9AQ² = 9AC² + 9CQ²

⇒ 9AQ² = 9AC² + (3CQ)² .......(i)

Given, BQ : CQ = 1 : 2

$\Rightarrow \dfrac{CQ}{BC} = \dfrac{CQ}{BQ + CQ} \\[1em] = \dfrac{2}{1 + 2} = \dfrac{2}{3} \\[1em] \Rightarrow \dfrac{CQ}{BC} = \dfrac{2}{3} \\[1em] \Rightarrow 3CQ = 2BC$

Substituting above value in (i) we get,

⇒ 9AQ² = 9AC² + (2BC)²

⇒ 9AQ² = 9AC² + 4BC².

Hence, proved that 9AQ² = 9AC² + 4BC².

(ii) In right angle triangle BPC,

By pythagoras theorem we get,

⇒ BP² = BC² + CP²

Multiplying both sides by 9 we get,

⇒ 9BP² = 9BC² + 9CP²

⇒ 9BP² = 9BC² + (3CP)² .......(ii)

Given, AP : PC = 1 : 2

$\Rightarrow \dfrac{CP}{AC} = \dfrac{CP}{AP + PC} \\[1em] = \dfrac{2}{1 + 2} = \dfrac{2}{3} \\[1em] \Rightarrow \dfrac{CP}{AC} = \dfrac{2}{3} \\[1em] \Rightarrow 3CP = 2AC$

Substituting above value in (ii) we get,

⇒ 9BP² = 9BC² + (2AC)²

⇒ 9BP² = 9BC² + 4AC².

Hence, proved that 9BP² = 9BC² + 4AC².

(iii) In right angle triangle ABC,

By pythagoras theorem we get,

⇒ AB² = AC² + BC² ......(iii)

Adding resultants from part (i) and (ii) we get,

9AQ² + 9BP² = 9AC² + 4BC² + 9BC² + 4AC²

9(AQ² + BP²) = 13AC² + 13BC²

9(AQ² + BP²) = 13(AC² + BC²)

9(AQ² + BP²) = 13AB² [From (iii)].

Hence, proved that 9(AQ² + BP²) = 13AB².

In the adjoining figure, △PQR is right angled at Q and points S and T trisect side QR. Prove that

8PT² = 3PR² + 5PS².

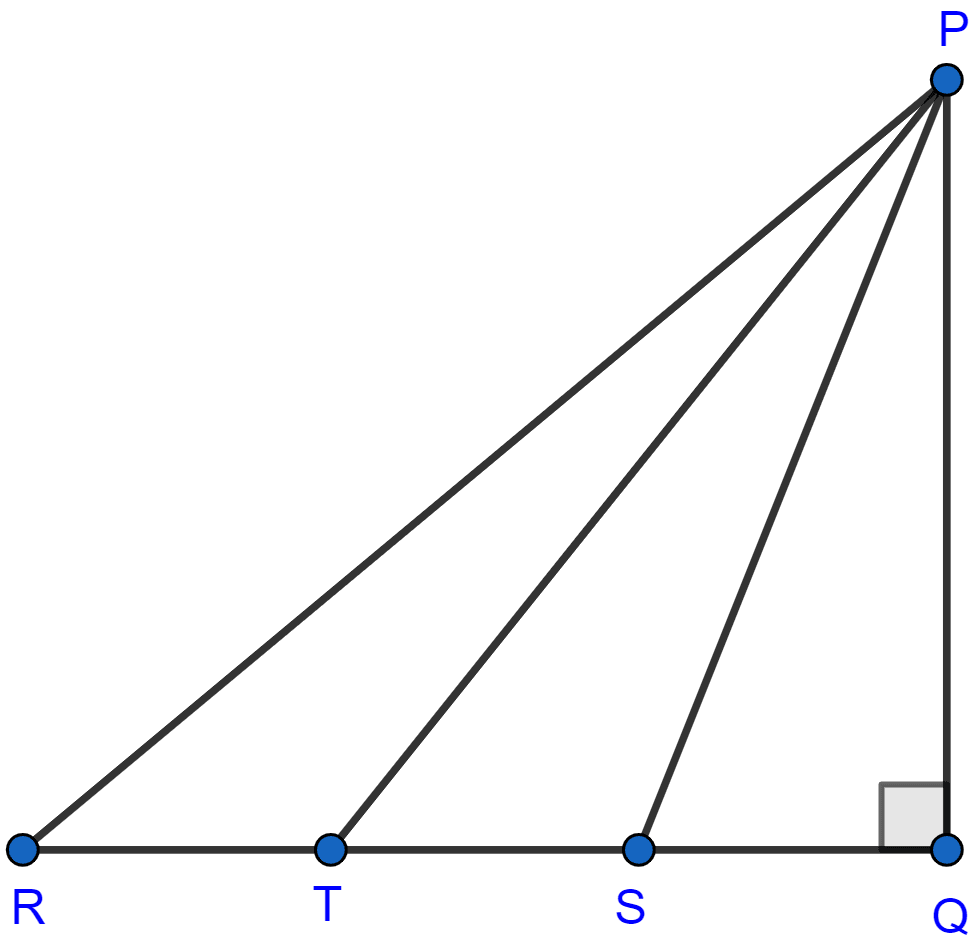
Answer

Let RT = TS = SQ = x

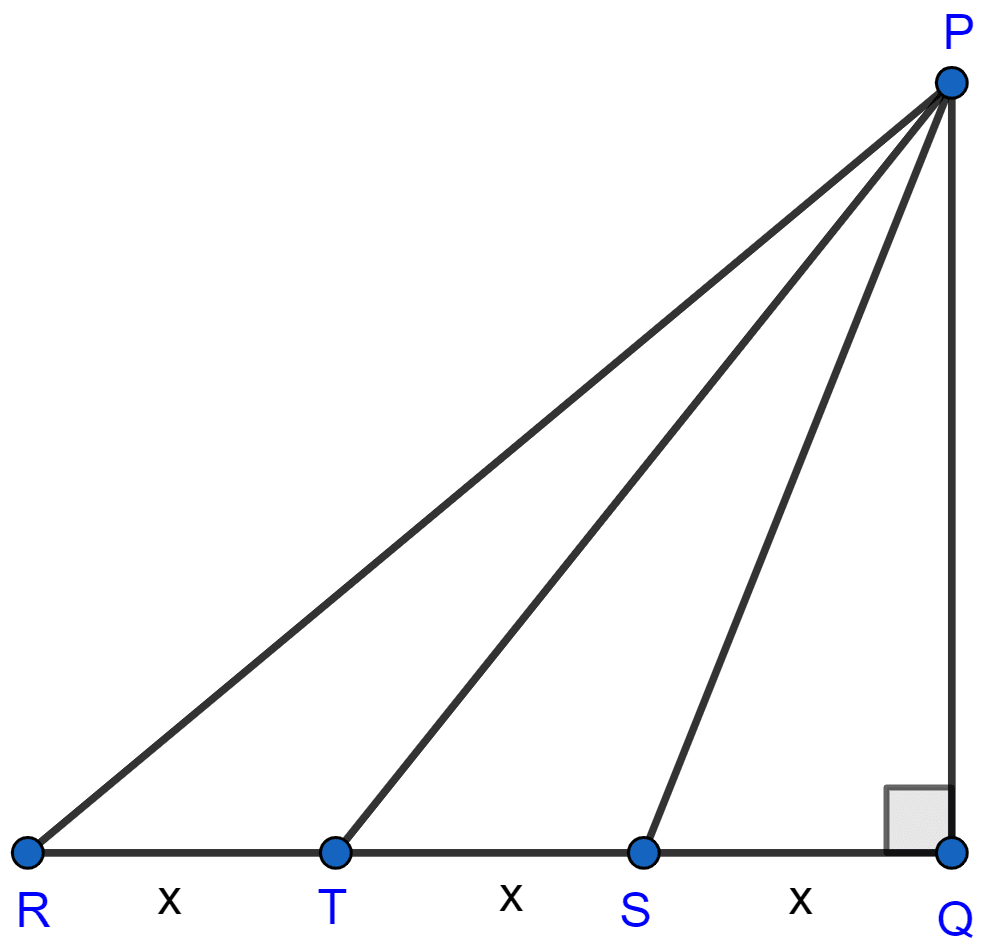
In right angle triangle PQR,

By pythagoras theorem we get,

⇒ PR² = QR² + PQ²

⇒ PR² = (3x)² + PQ²

⇒ PR² = 9x² + PQ²

Multiplying above equation by 3 we get,

⇒ 3PR² = 27x² + 3PQ² .......(i)

In right angle triangle PTQ,

By pythagoras theorem we get,

⇒ PT² = QT² + PQ²

⇒ PT² = (2x)² + PQ²

⇒ PT² = 4x² + PQ²

Multiplying above equation by 8 we get,

⇒ 8PT² = 32x² + 8PQ² .......(ii)

In right angle triangle PSQ,

By pythagoras theorem we get,

⇒ PS² = SQ² + PQ²

⇒ PS² = (x)² + PQ²

⇒ PS² = x² + PQ²

Multiplying above equation by 5 we get,

⇒ 5PS² = 5x² + 5PQ² .......(iii)

Adding (i) and (iii) we get,

⇒ 3PR² + 5PS² = 27x² + 5x² + 3PQ² + 5PQ²

⇒ 3PR² + 5PS² = 32x² + 8PQ²

From (ii) we get,

⇒ 3PR² + 5PS² = 8PT².

Hence, proved that 8PT² = 3PR² + 5PS².

In a quadrilateral ABCD, ∠B = 90°. If AD² = AB² + BC² + CD², Prove that ∠ACD = 90°.

Answer

In right angle triangle ABC,

By pythagoras theorem,

AC² = AB² + BC² .......(i)

Given,

AD² = AB² + BC² + CD²

Putting value of AB² + BC² from eqn (i) we get,

AD² = AC² + CD²

∴ △ACD is a right angled triangle.

In △ACD,

∠ACD = 90° i.e. angle opposite to hypotenuse = 90° (By converse of pythagoras theorem.)

Hence, proved that ∠ACD = 90°.

In the adjoining figure, find the length of AD in terms of b and c.

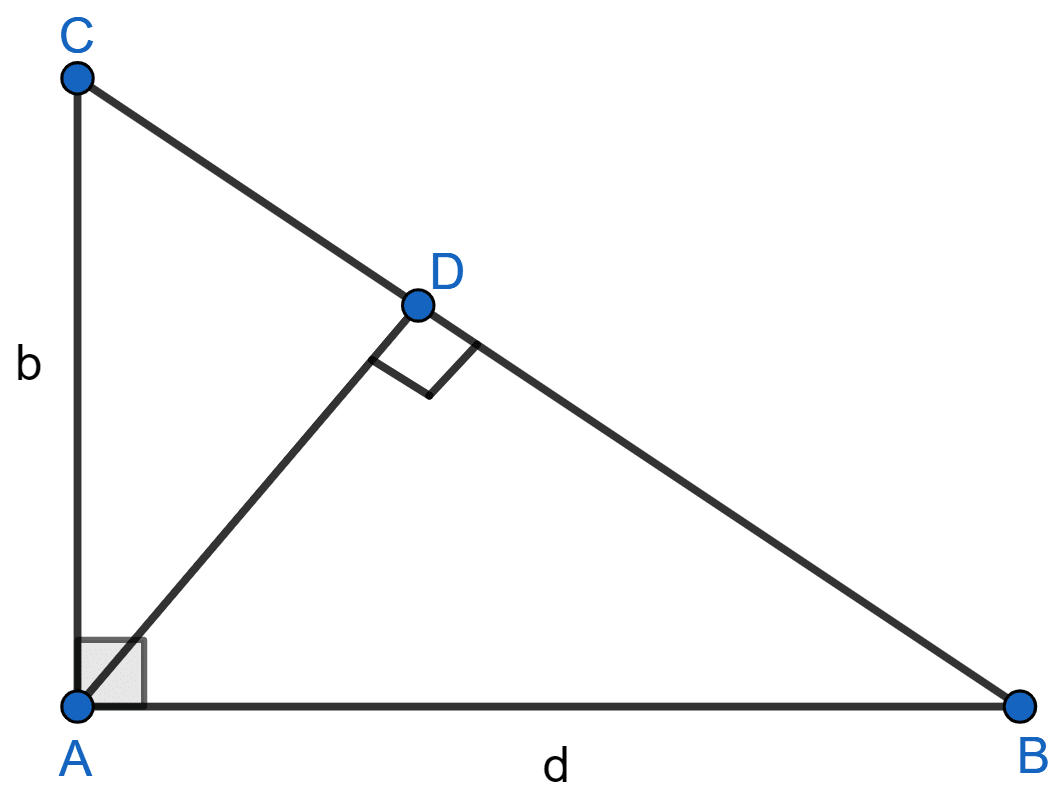
Answer

In right angle triangle ABC,

By pythagoras theorem,

BC² = AB² + AC²

BC² = c² + b²

BC = $\sqrt{b^2 + c^2}$.

From figure,

Area of △ABC = Area of △ABD + Area of △ADC

⇒ $\dfrac{1}{2}$ x AB x AC = $\dfrac{1}{2}$ x AD x BD + $\dfrac{1}{2}$ x AD x CD

⇒ $\dfrac{1}{2}$(AB.AC) = $\dfrac{1}{2}$(AD.BD + AD.CD)

⇒ AB.AC = AD.BD + AD.CD

⇒ AB.AC = AD(BD + CD)

⇒ AB.AC = AD.BC [∵ BD + CD = BC]

⇒ AD = $\dfrac{\text{AB.AC}}{\text{BC}}$

Putting values of AB, AC and BC in above equation we get,

AD = $\dfrac{c.b}{\sqrt{b^2 + c^2}}$

Hence, AD = $\dfrac{bc}{\sqrt{b^2 + c^2}}$.

ABCD is a square, F is mid-point of AB and BE is one third of BC. If area of △FBE is 108 cm², find the length of AC.

Answer

Let x cm be the side of each square.

Since, F is midpoint of AB so, FB = $\dfrac{x}{2}$ cm

BE is one third of BC, BE = $\dfrac{x}{3}$.

Given, area of △FBE is 108 cm²

$\therefore \dfrac{1}{2} \times FB \times BE = 108 \\[1em] \Rightarrow \dfrac{1}{2} \times \dfrac{x}{2} \times \dfrac{x}{3} = 108 \\[1em] \Rightarrow \dfrac{x^2}{12} = 108 \\[1em] \Rightarrow x^2 = 1296 \\[1em] \Rightarrow x = \sqrt{1296} = 36.$

Length of diagonal of square = $\sqrt{2}$ Side = $36\sqrt{2}$ cm.

Hence, length of diagonal of square = $36\sqrt{2}$ cm.

In a triangle ABC, AB = AC and D is a point on side AC such that BC² = AC × CD.

Prove that BD = BC.

Answer

Draw BE ⊥ AC.

In right triangle BEC,

By pythagoras theorem,

⇒ BC² = BE² + EC²

⇒ BC² = BE² + (AC - AE)²

⇒ BC² = BE² + AC² + AE² - 2AC.AE .........(i)

In right triangle ABE,

By pythagoras theorem,

⇒ AB² = BE² + AE².........(ii)

Substituting value of BE² + AE² from (ii) in (i) we get,

⇒ BC² = AB² + AC² - 2AC.CE

⇒ BC² = AC² + AC² - 2AC.AE [∵ AB = AC]

⇒ BC² = 2AC² - 2AC.AE

⇒ BC² = 2AC(AC - AE)

⇒ BC² = 2AC × EC .........(iii)

Given, BC² = AC × CD ..........(iv)

Comparing (iii) and (iv) we get,

⇒ 2AC × EC = AC × CD

⇒ 2EC = CD or EC = $\dfrac{\text{CD}}{2}$

So, we can say that ED = EC as E is mid-point of CD.

In △BDE and △BCE,

BE = BE (Common)

ED = EC

∠BED = ∠BEC = 90°

△BDE ≅ △BCE by SAS axiom of congruency.

We know that corresponding parts of congruent triangle are equal.

∴ BD = BC.

Hence, proved that BD = BC.