Triangles

Which of the following pairs of triangles are congruent ?

(a) △ABC and △DEF in which : BC = EF, AC = DF and ∠C = ∠F.

(b) △ABC and △PQR in which : AB = PQ, BC = QR and ∠C = ∠R.

(c) △ABC and △LMN in which : ∠A = ∠L = 90°, AB = LM, ∠C = 40° and ∠M = 50°

(d) △ABC and △DEF in which : ∠B = ∠E = 90°, AC = DF

Answer

(a) In △ABC and △DEF,

⇒ BC = EF [Given]

⇒ AC = DF [Given]

⇒ ∠C = ∠F [Given]

∴ △ABC ≅ △DEF (By S.A.S axiom)

Hence, △ABC and △DEF are congruent by S.A.S axiom.

(b) Given,

In △ABC and △PQR,

⇒ AB = PQ [Given]

⇒ BC = QR [Given]

⇒ ∠C = ∠R [Given]

Here the equal angles are not the included angles, thus the triangles are not necessarily congruent.

Hence, △ABC and △PQR are not necessarily congruent.

(c) Given,

In △ABC,

⇒ ∠A + ∠B + ∠C = 180°

⇒ 90° + ∠B + 40° = 180°

⇒ ∠B + 130° = 180°

⇒ ∠B = 180° - 130°

⇒ ∠B = 50°.

In △ABC and △LMN,

⇒ AB = LM [Given]

⇒ ∠B = ∠M [Both equal to 50°]

⇒ ∠A = ∠L [Both equal to 90°]

∴ △ABC ≅ △LMN (By A.S.A axiom)

Hence, △ABC and △LMN are congruent by A.S.A axiom.

(d) Given,

In △ABC and △DEF,

⇒ ∠B = ∠E = 90°

⇒ AC = DF

⇒ AB = DE

∴ △ABC ≅ △DEF (By R.H.S. axiom)

Hence, △ABC and △DEF are congruent by R.H.S. axiom.

In the given figure, P is a point in the interior of ∠ABC. If PL ⊥ BA and PM ⊥ BC such that PL = PM, prove that BP is the bisector of ∠ABC.

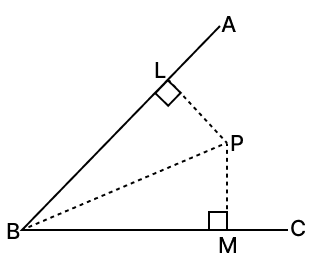
Answer

Given,

In △BLP and △BMP,

⇒ ∠L = ∠M = 90°

⇒ PL = PM [Given]

⇒ PB = PB [Common side]

∴ △BLP ≅ △BMP (By R.H.S. axiom)

⇒ ∠LBP = ∠PBM [Corresponding angles of congruent triangles are equal.]

Hence, proved that BP is the bisector of ∠ABC.

In the given figure, equal sides BA and CA of △ABC are produced to Q and P respectively such that AP = AQ. Prove that PB = QC.

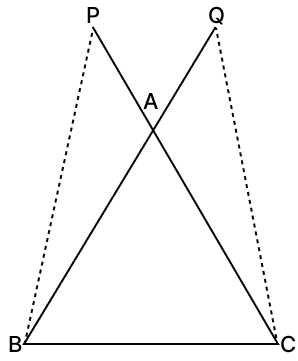
Answer

In △ ABC,

⇒ BA = CA [Given]

⇒ ∠ABC = ∠ACB [Angles opposite to equal sides are equal]

From figure,

⇒ ∠PAB + ∠CAB = 180° [Linear pair of angles]

⇒ ∠PAB = 180° - ∠CAB ......(1)

⇒ ∠QAC + ∠CAB = 180° [Linear pair of angles]

⇒ ∠QAC = 180° - ∠CAB ......(2)

From eq.(1) and (2), we have:

⇒ ∠PAB = ∠QAC

In △PAB and △QAC,

⇒ ∠PAB = ∠QAC [Proved above]

⇒ AP = AQ [Given]

⇒ BA = CA [Given]

∴ △PAB ≅ △QAC (By S.A.S axiom)

∴ PB = QC [Corresponding angles of congruent triangles are equal]

Hence, proved that PB = QC.

In the given figure, median AD of △ABC is produced. If BL and CM are perpendiculars drawn on AD and AD produced, prove that BL = CM.

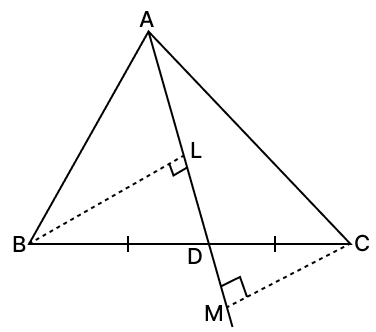
Answer

In △ABC,

AD is the median on side BC

⇒ BD = DC

In △LDB and △CDM,

⇒ BD = DC [Given, AD is the median]

⇒ ∠L = ∠M [Each equal to 90°]

⇒ ∠LDB = ∠CDM [Vertically opposite angles are equal]

∴ △LDB ≅ △CDM (By A.A.S. axiom)

⇒ BL = CM [Corresponding part of congruent triangles are equal.]

Hence, proved that BL = CM.

In the given figure, M is the mid-point of AB and CD. Prove that CA = BD and CA || BD.

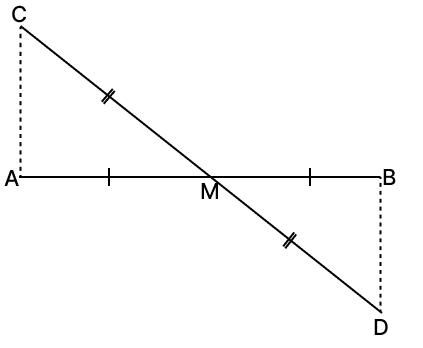
Answer

Given,

M is the mid-point of AB and CD.

Thus, MC = MD and MB = MA

In △MAC and △MBD,

⇒ MA = MB [Proved above]

⇒ MC = MD [Proved above]

⇒ ∠CMA = ∠BMD [Vertically opposite angles are equal]

∴ △MAC ≅ △MBD (By S.A.S. axiom)

⇒ CA = BD [Corresponding part of congruent triangles are equal.]

⇒ ∠CAM = ∠DBM [Corresponding part of congruent triangles are equal.]

Since, ∠CAM and ∠DBM are alternate angles and since they are equal,

∴ CA || BD

Hence, proved that CA = BD and CA || BD.

In the given figure, PA ⊥ AB; QB ⊥ AB and PA = QB. If PQ intersects AB at M, show that M is the mid-point of both AB and PQ.

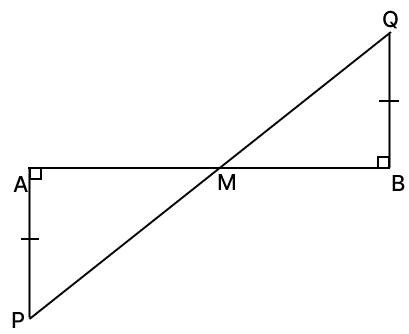
Answer

Given,

⇒ PA = QB

From figure,

⇒ ∠PAM = ∠QBM = 90°

In △MAP and △MBQ,

⇒ ∠PAM = ∠QBM [Both equal to 90°]

⇒ AP = BQ [Given]

⇒ ∠AMP = ∠QMB [Vertically opposite angles are equal]

∴ △MAP ≅ △MBQ (By A.A.S axiom)

⇒ AM = MB [Corresponding parts of congruent triangles are equal]

⇒ PM = MQ [Corresponding parts of congruent triangles are equal]

Thus, M is the mid-point of both AB and PQ.

Hence, proved that M is the mid-point of both AB and PQ.

AB is a line segment. AX and BY are two equal line segments drawn on opposite sides of AB such that AX || YB. If AB and XY intersect at M, prove that :

(i) △AMX ≅ △BMY

(ii) AB and XY bisect each other at M.

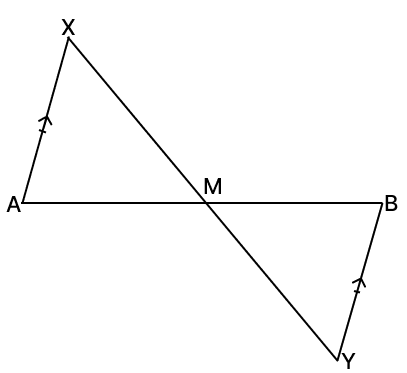
Answer

(i) In △AMX and △BMY,

⇒ ∠AXM = ∠BYM [Alternate angles are equal as AX || YB]

⇒ AX = BY [Given]

⇒ ∠AMX = ∠BMY [Vertically opposite angles are equal]

∴ △AMX ≅ △BMY (By A.A.S axiom)

Hence, proved that △AMX ≅ △BMY.

(ii) As, △AMX ≅ △BMY

⇒ AM = MB [Corresponding parts of congruent triangles are equal]

∴ M is the mid-point of line segment AB.

⇒ XM = MY [Corresponding parts of congruent triangles are equal]

∴ M is the mid-point of line segment XY.

Hence, proved that AB and XY bisect each other at M.

In the given figure, the sides BA and CA of △ABC have been produced to D and E such that BA = AD and CA = AE. Prove that, ED || BC.

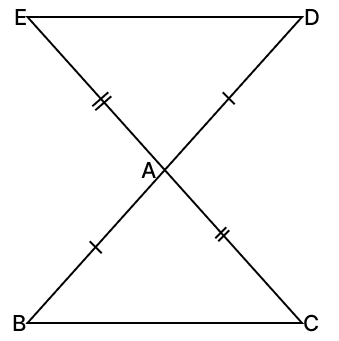
Answer

In △ABC and △ADE,

⇒ AB = AD [Given]

⇒ AC = AE [Given]

⇒ ∠BAC = ∠EAD [Vertically opposite angles are equal]

∴ △ABC ≅ △ADE [By S.A.S axiom]

⇒ ∠ABC = ∠ADE [Corresponding parts of congruent triangles are equal.]

From figure,

∠ABC and ∠ADE are alternate angles and since they are equal.

∴ ED || BC

Hence, proved that ED || BC.

In the given figure, the line segments AB and CD intersect at a point M in such a way that AM = MD and CM = MB. Prove that, AC = BD but AC may not be parallel to BD.

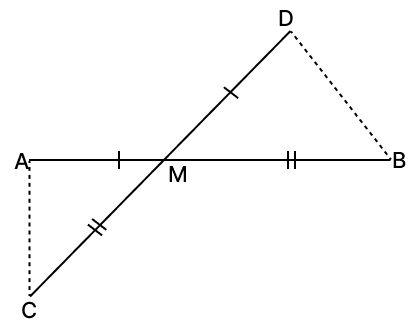
Answer

In △MAC and △MDB,

⇒ AM = MD [Given]

⇒ CM = MB [Given]

⇒ ∠AMC = ∠DMB [Vertically opposite angles are equal]

∴ △MAC ≅ △MDB (By S.A.S axiom)

⇒ AC = BD [Corresponding parts of congruent triangles are equal.]

⇒ ∠MDB = ∠MAC [Corresponding parts of congruent triangles are equal.]

∴ ∠MDB ≠ ∠MCA

Thus, we cannot prove that AC // BD.

Hence, proved that AC = BD but AC may not be parallel to BD.

If two altitudes of a triangle are equal, prove that it is an isosceles triangle.

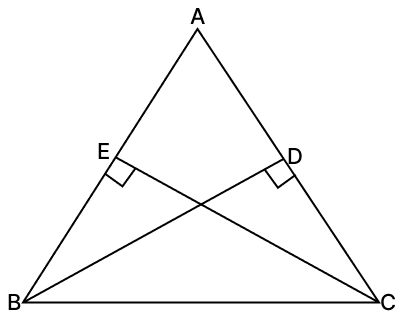
Answer

Given,

CE = BD [Altitudes of △ABC are equal]

In △ABD and △ACE,

⇒ ∠ADB = ∠AEC [Each equal to 90°]

⇒ CE = BD [Given]

⇒ ∠DAB = ∠EAC [Common angle]

∴ △ABD ≅ △ACE (∵ A.A.S. axiom)

⇒ AB = AC [Corresponding parts of congruent triangles are equal]

Since, two sides are equal.

Hence, △ABC is an isosceles triangle with AB = AC.

In the given figure, ∠BAC = ∠CDB and ∠BCA = ∠CBD. Prove that AB = CD.

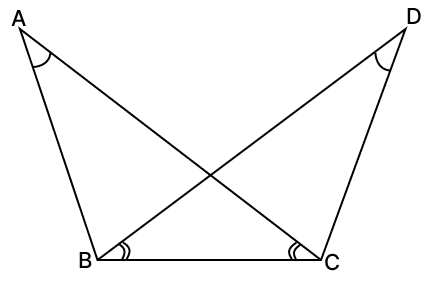
Answer

In △DCB and △ABC,

⇒ ∠DBC = ∠ACB [Given]

⇒ ∠BDC = ∠BAC [Given]

⇒ BC = BC [Common side]

∴ △ABC ≅ △DCB (By A.A.S. axiom)

⇒ AB = DC [Corresponding parts of congruent triangles are equal]

Hence, proved that AB = CD.

In the given figure, ∠ABD = ∠EBC, BD = BC and ∠ACB = ∠EDB. Prove that AB = BE.

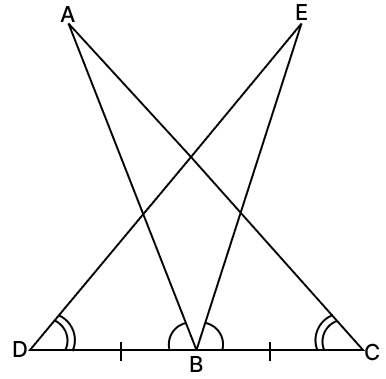
Answer

Given,

∠ACB = ∠EDB and ∠ABD = ∠EBC

From figure,

⇒ ∠EBD = ∠ABE + ∠ABD .....(1)

Also,

⇒ ∠ABC = ∠ABE + ∠EBC

⇒ ∠ABC = ∠ABE + ∠ABD .....(2)

From eq.(1) and (2), we have :

⇒ ∠ABC = ∠EBD

In △EDB and △ACB,

⇒ DB = BC [Given]

⇒ ∠ABC = ∠EBD [Proved above]

⇒ ∠ACB = ∠EDB [Given]

∴ △EDB ≅ △ACB (By A.S.A. axiom)

⇒ AB = BE [Corresponding parts of congruent triangles are equal.]

Hence, proved that AB = BE.

In the given figure, AY ⊥ ZY nd BY ⊥ XY such that AY = ZY and BY = XY. Prove that AB = ZX.

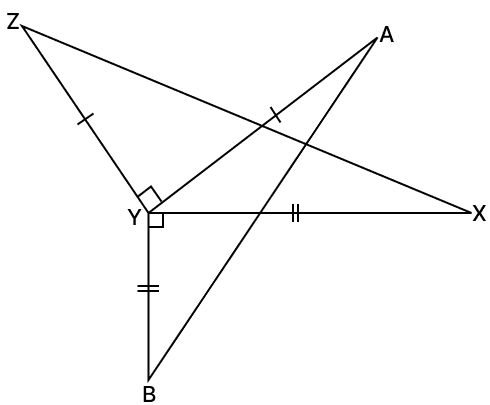
Answer

⇒ ∠AYZ = ∠XYB [Each equal to 90°]

Adding ∠AYX on both L.H.S and R.H.S, we have:

⇒ ∠AYZ + ∠AYX = ∠XYB + ∠AYX

⇒ ∠XYZ = ∠AYB

In △XYZ and △AYB,

⇒ ZY = AY [Given]

⇒ XY = BY [From figure]

⇒ ∠XYZ = ∠AYB [Proved above]

∴ △XYZ ≅ △AYB (By S.A.S axiom)

⇒ AB = ZX [Corresponding parts of congruent triangles are equal]

Hence, proved that AB = ZX.

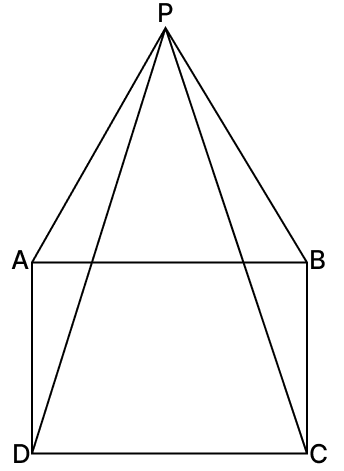
In the given figure, ABCD is a square and △PAB is an equilateral triangle.

(i) Prove that △APD ≅ △BPC.

(ii) Show that ∠DPC = 15°.

Answer

(i) We know that,

Each interior angle in a square is 90° and each interior angle in an equilateral triangle is 60°.

From figure,

⇒ ∠DAP = ∠DAB + ∠BAP

⇒ ∠DAP = 90° + 60° = 150°

⇒ ∠CBP = ∠CBA + ∠ABP

⇒ ∠CBP = 90° + 60° = 150°

In △APD and △BPC,

⇒ ∠DAP = ∠CBP [Each equal to 150°]

⇒ AD = BC [Sides of a square]

⇒ AP = BP [Sides of an equilateral triangle]

∴ △APD ≅ △BPC (By S.A.S axiom)

Hence, △APD ≅ △BPC.

(ii) ABCD is a square.

∴ AB = AD = DC = BC

APB is an equilateral triangle.

∴ AP = PB = AB

So, we get :

AP = AD and PB = BC

∴ △APD and △BPC are isosceles triangle.

We know that,

Angles opposite to equal sides are equal.

∴ ∠APD = ∠ADP = x (let) and ∠BPC = ∠BCP = y (let)

In △APD,

By angle sum property of triangle,

⇒ ∠APD + ∠ADP + ∠DAP = 180°

⇒ x + x + 150° = 180°

⇒ 2x = 180° - 150°

⇒ 2x = 30°

⇒ x = $\dfrac{30°}{2}$

⇒ x = 15°.

In △BPC,

By angle sum property of triangle,

⇒ ∠BPC + ∠BCP + ∠PBC = 180°

⇒ y + y + 150° = 180°

⇒ 2y = 180° - 150°

⇒ 2y = 30°

⇒ y = $\dfrac{30°}{2}$

⇒ y = 15°

From figure,

⇒ ∠PDC = ∠ADC - ∠ADP = 90° - 15° = 75°

⇒ ∠PCD = ∠BCD - ∠BCP = 90° - 15° = 75°

In △DPC,

By angle sum property of triangle,

⇒ ∠DPC + ∠PDC + ∠PCD = 180°

⇒ ∠DPC + 75° + 75° = 180°

⇒ ∠DPC + 150° = 180°

⇒ ∠DPC = 180° - 150°

⇒ ∠DPC = 30°.

Hence, proved that ∠DPC = 30°.

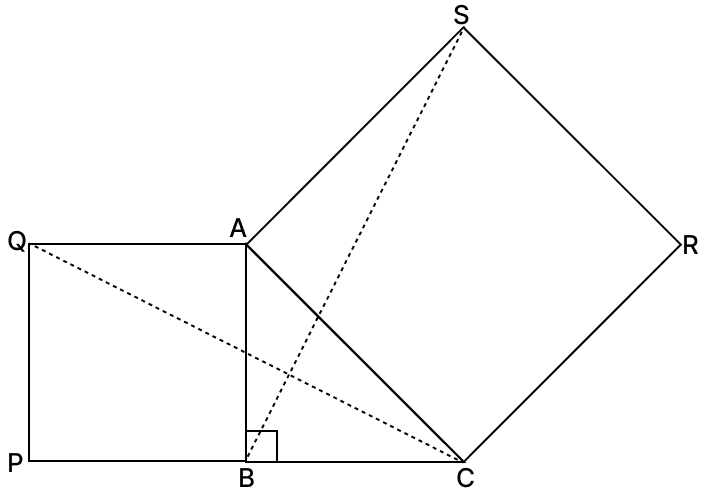
In the given figure, in △ABC, ∠B = 90°. If ABPQ and ACRS are squares, prove that:

(i) △ACQ ≅ △ABS

(ii) CQ = BS.

Answer

(i) From figure,

In △ACQ,

⇒ ∠BAC = ∠QAC - ∠QAB

⇒ ∠QAC = ∠BAC + ∠QAB

⇒ ∠QAC = ∠BAC + 90° ....(1)

In △ABS,

⇒ ∠BAC = ∠BAS - ∠CAS

⇒ ∠BAS = ∠BAC + ∠CAS

⇒ ∠BAS = ∠BAC + 90° ....(2)

From eq.(1) and (2), we have:

⇒ ∠QAC = ∠BAS

In △ACQ and △ABS,

⇒ ∠QAC = ∠BAS [Proved above]

⇒ AQ = AB [Sides of square ABPQ]

⇒ AC = AS [Sides of square ACRS]

∴ △ACQ ≅ △ABS (By S.A.S axiom)

Hence, proved that △ACQ ≅ △ABS.

(ii) As,

△ACQ ≅ △ABS

∴ CQ = BS [Corresponding parts of congruent triangles are equal]

Hence, proved that CQ = BS.

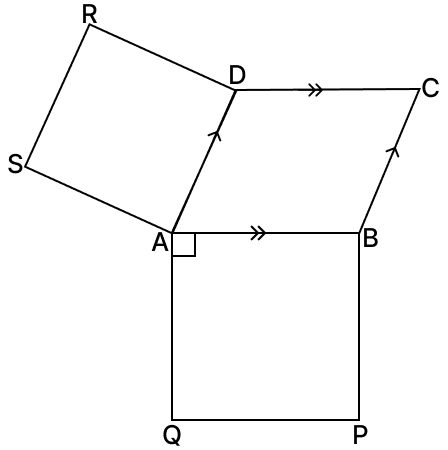
Squares ABPQ and ADRS are drawn on the sides AB and AD of a parallelogram ABCD. Prove that:

(i) ∠SAQ = ∠ABC

(ii) SQ = AC.

Answer

(i) Given,

ABPQ and ADRS are square.

Each angle of a square = 90°

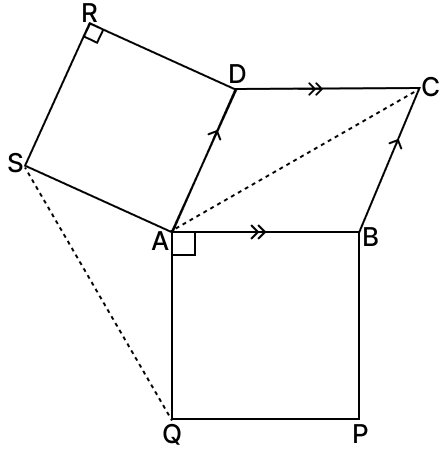
From figure,

⇒ ∠SAQ + ∠SAD + ∠BAD + ∠BAQ = 360°

⇒ ∠SAQ + 90° + ∠BAD + 90° = 360°

⇒ ∠SAQ + ∠BAD + 180° = 360°

⇒ ∠SAQ + ∠BAD = 360° - 180°

⇒ ∠SAQ = 180° - ∠BAD ...(1)

In parallelogram ABCD,

⇒ ∠ABC + ∠BAD = 180° (Sum of adjacent angles of a // gm = 180°)

⇒ ∠ABC = 180° - ∠BAD ....(2)

From eq.(1) and (2), we have:

⇒ ∠SAQ = ∠ABC

Hence, proved that ∠SAQ = ∠ABC.

(ii) In square ADRS,

AS = SR = RD = AD

⇒ AD = BC (Opposite sides of a parallelogram ABCD are equal)

∴ AS = BC

In △SAQ and △CBA,

⇒ ∠SAQ = ∠ABC (Proved above)

⇒ AS = BC (Proved above)

⇒ AQ = AB (Sides of a square ABPQ)

∴ △SAQ ≅ △CBA (By S.A.S axiom)

⇒ SQ = AC (Corresponding parts of congruent triangles are equal)

Hence, proved that SQ = AC.

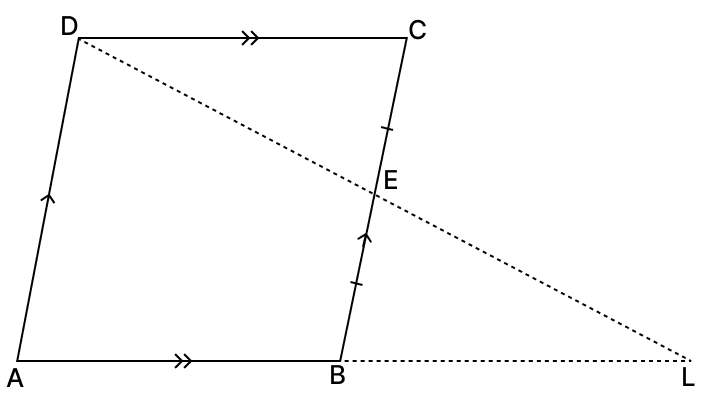
In the given figure, ABCD is a parallelogram, E is the mid-point of BC. DE produced meets AB produced at L. Prove that:

(i) AB = BL

(ii) AL = 2DC

Answer

(i) Given,

ABCD is a parallelogram.

We know that,

Opposite sides of a parallelogram are equal.

⇒ AB = CD and AD = BC

In △DEC and △BEL,

⇒ ∠LBE = ∠DCE (Alternate angles, since AB || DC)

⇒ EC = EB (Given)

⇒ ∠DEC = ∠BEL (Vertically opposite angles are equal)

∴ △DEC ≅ △BEL (By A.S.A axiom)

⇒ DC = BL (Corresponding parts of congruent triangles are equal)

Since, AB = DC

∴ AB = BL.

Hence, proved that AB = BL.

(ii) From figure,

⇒ AL = AB + BL

⇒ AL = DC + DC

⇒ AL = 2DC.

Hence, proved that AL = 2DC.

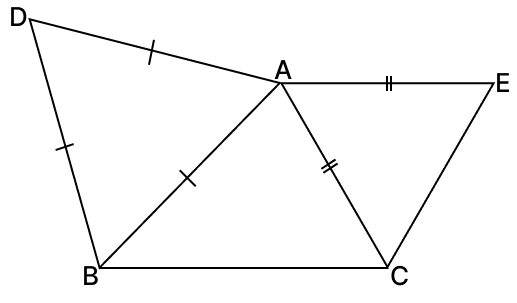
Equilateral triangle ABD and ACE are drawn on the sides AB and AC of △ABC as shown in the figure. Prove that :

(i) ∠DAC = ∠EAB

(ii) DC = BE

Answer

(i) Given,

△ABD and △ACE are equilateral triangles.

⇒ ∠DAB = ∠ABD = ∠BDA = ∠EAC = ∠ACE = ∠CEA = 60°

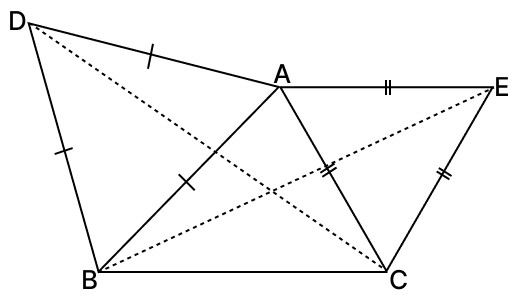
From figure,

∠DAC = ∠DAB + ∠BAC

⇒ ∠DAC = 60° + ∠BAC .....(1)

∠EAB = ∠EAC + ∠BAC

⇒ ∠EAB = 60° + ∠BAC .....(2)

From eq.(1) and (2), we have :

⇒ ∠EAB = ∠DAC

Hence, proved that, ∠EAB = ∠DAC.

(ii) In △DAC and △BAE,

⇒ ∠EAB = ∠DAC (Proved above)

⇒ AD = AB (Sides of an equilateral triangle)

⇒ AC = AE (Sides of an equilateral triangle)

∴ △DAC ≅ △BAE (By S.A.S axiom)

∴ DC = BE (Corresponding parts of congruent triangles are equal)

Hence, proved that DC = BE.

In the given figure, ABCD is a square and P, Q, R are points on AB, BC and CD respectively such that AP = BQ = CR and ∠PQR = 90°. Prove that:

(i) PB = QC

(ii) PQ = QR

(iii) ∠QPR = 45°

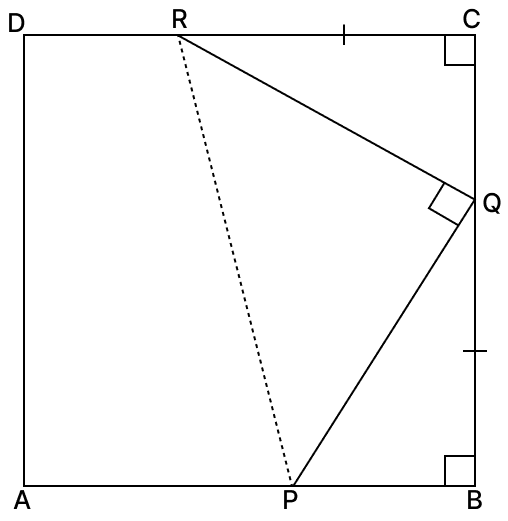
Answer

(i) Given,

ABCD is a square.

AB = BC = CD = DA

Given,

AP = BQ = CR

From figure,

⇒ PB = AB - AP ....(1)

⇒ QC = BC - BQ

⇒ QC = AB - AP [As, BC = AB and BQ = AP] ....(2)

From eq.(1) and (2), we have :

⇒ PB = QC

Hence, proved that PB = QC.

(ii) In △PBQ and △QCR,

⇒ ∠PBQ = ∠QCR (Both equal to 90°)

⇒ BQ = CR (Given)

⇒ PB = QC (Proved above)

∴ △PBQ ≅ △QCR (By S.A.S axiom)

∴ PQ = QR (Corresponding parts of congruent triangles are equal)

Hence, proved that PQ = QR.

(iii) In △QPR,

⇒ PQ = QR

∴ △PQR is an isosceles triangle.

⇒ ∠QPR = ∠QRP = f (let) (Angles opposite to equal sides are equal)

By angle sum property of triangle,

⇒ ∠QPR + ∠QRP + ∠PQR = 180°

⇒ f + f + 90° = 180°

⇒ 2f = 180° - 90°

⇒ 2f = 90°

⇒ f = $\dfrac{90°}{2}$

⇒ f = 45°.

⇒ ∠QPR = ∠QRP = 45°.

Hence, proved that ∠QPR = 45°.

In the given figure, ABCD is a square, EF || BD and R is the mid-point of EF. Prove that:

(i) BE = DF

(ii) AR bisects ∠BAD

(iii) If AR is produced, it will pass through C.

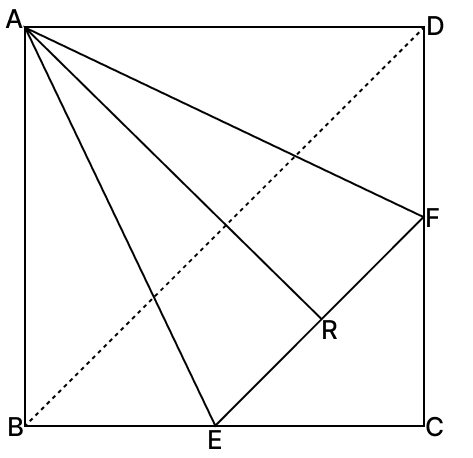
Answer

(i) Given,

EF || BD

DC is the transversal.

⇒ ∠BDC = ∠EFC

BC is the transversal.

⇒ ∠DBC = ∠FEC

Given,

ABCD is a square.

⇒ ∠A = ∠B = ∠C = ∠D = 90°

In △BDC,

BC = DC [Sides of a square are equal]

⇒ ∠DBC = ∠CDB = x (let) [Angles opposite to equal sides are equal]

By angle sum property of triangle,

⇒ ∠DBC + ∠BCD + ∠CDB = 180°

⇒ x + 90° + x = 180°

⇒ 2x = 180° - 90°

⇒ x = $\dfrac{90°}{2}$

⇒ x = 45°

⇒ ∠DBC = ∠CDB = 45°

∴ ∠DBC = ∠CDB = ∠FEC = ∠EFC = 45°.

⇒ △BDC and △EFC are isosceles triangles.

⇒ EC = CF (As, ∠FEC = ∠EFC)

From figure,

⇒ BE = BC - EC .....(1)

⇒ DF = DC - CF

As, BC = DC and EC = CF

⇒ DF = BC - EC .....(2)

From (1) and (2), we get :

⇒ BE = DF.

Hence, proved that BE = DF.

(ii) In △ABE and △ADF,

⇒ ∠ABE = ∠ADF (Both equal to 90°)

⇒ AB = AD (Sides of a square)

⇒ BE = DF (Proved above)

∴ △ABE ≅ △ADF (By S.A.S axiom)

⇒ ∠BAE = ∠DAF (Corresponding parts of congruent triangles are equal)

⇒ AE = AF (Corresponding parts of congruent triangles are equal)

∴ △AEF is an isosceles triangle.

Given,

R is the mid-point of EF.

We know that,

In an isosceles triangle, the median to the base is also the angle bisector of the vertex angle.

∴ AR bisects ∠EAF.

⇒ ∠EAR = ∠FAR

From figure,

⇒ ∠BAR = ∠BAE + ∠EAR ....(1)

⇒ ∠DAR = ∠DAF + ∠FAR

Since,

∠EAR = ∠FAR and ∠BAE = ∠DAF.

⇒ ∠DAR = ∠BAE + ∠EAR .....(2)

From eq.(1) and (2), we have:

⇒ ∠BAR = ∠DAR.

∴ AR bisects ∠BAD.

Hence, proved that AR bisects ∠BAD.

(iii) Since, AR bisects ∠BAD

AR lies on diagonal AC, as diagonals of a square bisect the vertex angle.

∴ AR if produced, must pass through the vertex C.

Hence, proved that, if AR is produced, it will pass through C.

ABCD is a parallelogram in which ∠A and ∠C are obtuse. Points X and Y are taken on diagonal BD such that ∠AXD = ∠CYB = 90°. Prove that : XA = YC.

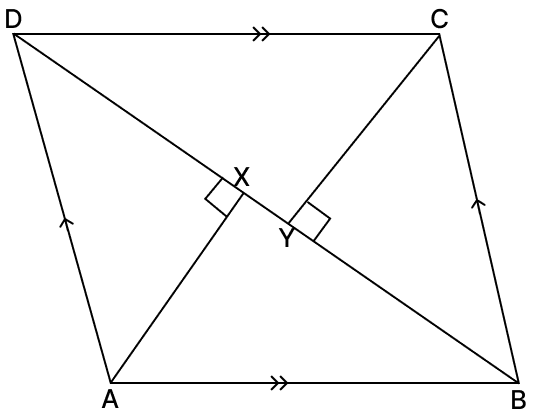
Answer

AD || BC and BD is the transversal.

⇒ ∠ADX = ∠CBY (Alternate interior angles are equal)

In △XAD and △YCB,

⇒ ∠ADX = ∠CBY (Proved above)

⇒ ∠AXD = ∠BYC (Both equal to 90°)

⇒ AD = BC (Opposite sides of a parallelogram are equal)

∴ △XAD ≅ △YCB (By A.A.S. axiom)

⇒ XA = YC (Corresponding parts of congruent triangles are equal)

Hence, proved that XA = YC.

ABCD is a parallelogram. The sides AB and AD are produced to E and F respectively such that AB = BE and AD = DF. Prove that △BEC ≅ △DCF.

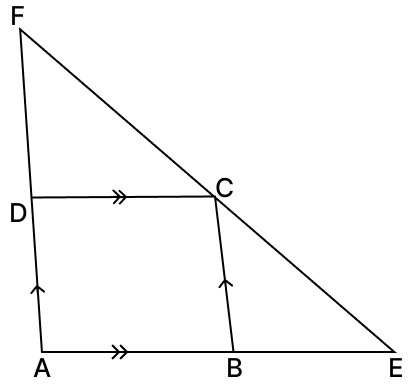
Answer Given,

AD = DF ....(1)

AB = BE ....(2)

We know that,

Opposite sides of parallelogram are equal.

∴ AD = BC ....(3)

∴ AB = CD ....(4)

From eq.(1) and (3), we get :

⇒ BC = DF

From eq.(2) and (4), we get :

⇒ BE = CD

We know that,

Opposite angles of a parallelogram are equal.

⇒ ∠ABC = ∠ADC = x (let)

From figure,

Since, AE is a straight line.

⇒ ∠CBE + ∠ABC = 180°

⇒ ∠CBE + x = 180°

⇒ ∠CBE = 180° - x .......(5)

Since, AF is a straight line.

⇒ ∠CDF + ∠ADC = 180°

⇒ ∠CDF + x = 180°

⇒ ∠CDF = 180° - x ........(6)

From eq.(5) and (6), we get :

⇒ ∠CBE = ∠CDF

In △BEC and △DCF,

⇒ BE = CD (Proved above)

⇒ ∠CBE = ∠CDF (Proved above)

⇒ BC = DF (Proved above)

∴ △BEC ≅ △DCF (By S.A.S axiom)

Hence, proved that △BEC ≅ △DCF.

The perpendicular bisectors of the sides of a △ABC meet at I. Prove that : IA = IB = IC.

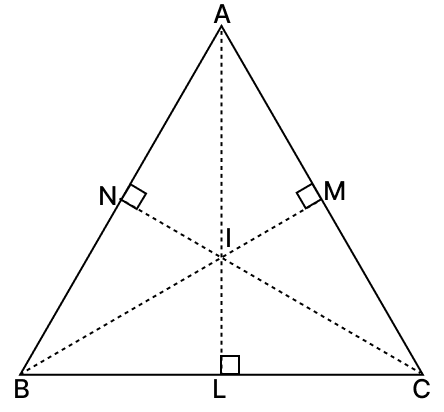
Answer From figure,

AL, CN and BM are perpendicular bisectors of sides BC, AB and AC respectively.

In △BIL and △CIL,

⇒ BL = LC (Since, AL is the perpendicular bisector of BC)

⇒ ∠BLI = ∠CLI (Both equal to 90°)

⇒ LI = LI (Common side)

∴ △BIL ≅ △CIL (By S.A.S axiom)

⇒ IB = IC .....(1) (Corresponding parts of congruent triangles are equal)

In △CIM and △AIM,

⇒ CM = AM (Since, BM is the perpendicular bisector of AC)

⇒ ∠CMI = ∠AMI (Both equal to 90°)

⇒ MI = MI (Common side)

∴ △CIM ≅ △AIM (By S.A.S axiom)

⇒ IC = IA .....(2) (Corresponding parts of congruent triangles are equal)

From eq.(1) and (2), we get:

⇒ IA = IB = IC.

Hence, proved that IA = IB = IC.

In a △ABC, AB = AC and ∠A = 50°, find ∠B and ∠C.

Answer

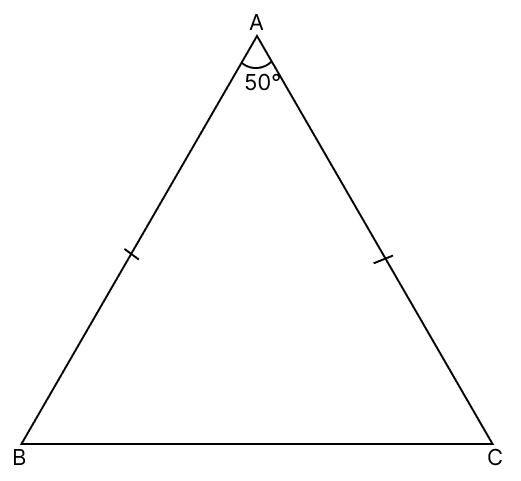
In △ABC,

AB = AC

⇒ ∠B = ∠C = a (let) [Angles opposite to equal sides are equal]

By angle sum property of a triangle,

⇒ ∠A + ∠B + ∠C = 180°

⇒ 50° + a + a = 180°

⇒ 2a = 180° - 50°

⇒ 2a = 130°

⇒ a = $\dfrac{130°}{2}$

⇒ a = 65°.

⇒ ∠B = ∠C = 65°

Hence, ∠B = ∠C = 65°.

In a △ABC, BC = AC and ∠B = 64°, find ∠C.

Answer

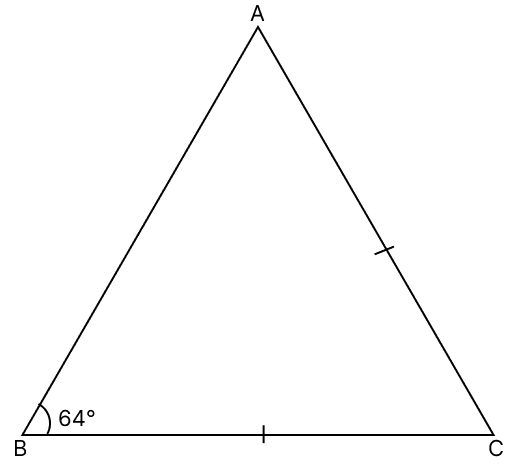
In △ABC,

BC = AC

⇒ ∠B = ∠A = 64° [Angles opposite to equal sides are equal]

By angle sum property of a triangle,

⇒ ∠A + ∠B + ∠C = 180°

⇒ 64° + 64° + ∠C = 180°

⇒ 128° + ∠C = 180°

⇒ ∠C = 180° - 128°

⇒ ∠C = 52°.

Hence, ∠C = 52°.

In each of the following figures, find the value of x :

(i)

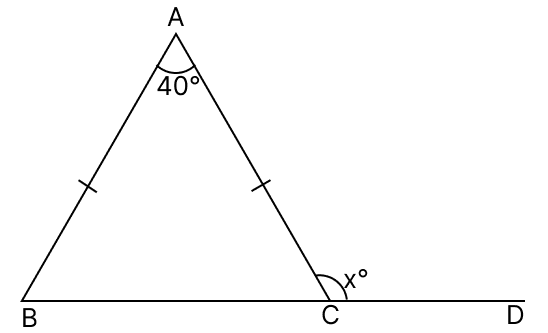
(ii)

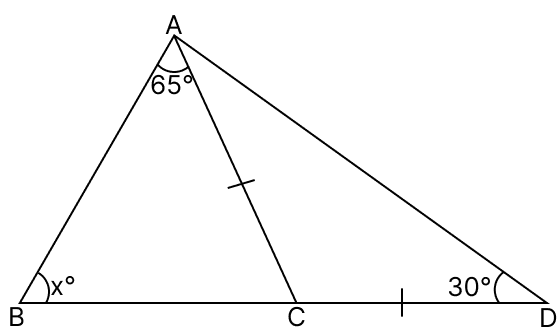
(iii)

Answer

(i) From figure,

∠A = 40°

In △ABC,

AB = AC

⇒ ∠C = ∠B = z (let) (Angles opposite to equal sides are equal)

By angle sum property of triangle,

⇒ ∠A + ∠B + ∠C = 180°

⇒ 40° + z + z = 180°

⇒ 2z = 180° - 40°

⇒ 2z = 140°

⇒ z = $\dfrac{140°}{2}$

⇒ z = 70°

⇒ ∠C = ∠B = 70°.

From figure,

⇒ ∠C + ∠ACD = 180° (Linear pair)

⇒ 70° + x° = 180°

⇒ x° = 180° - 70°

⇒ x° = 110°

⇒ x = 110.

Hence, the value of x = 110.

(ii) From figure,

In △CAD,

⇒ AC = CD

⇒ ∠CDA = ∠CAD = 30° (Angles opposite to equal sides are equal)

In △ABD,

By angle sum property of triangle,

⇒ ∠DBA + ∠BAD + ∠BDA = 180°

⇒ x° + ∠BAC + ∠CAD + ∠BDA = 180°

⇒ x° + 65° + 30° + 30° = 180°

⇒ x° + 125° = 180°

⇒ x° = 180° - 125°

⇒ x° = 55°

⇒ x = 55.

Hence, the value of x = 55.

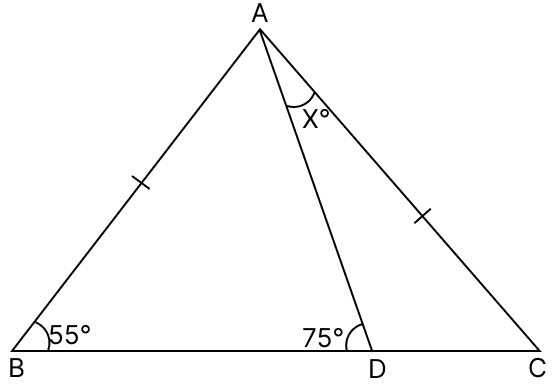
(iii) In △ABC,

AB = AC

⇒ ∠ABC = ∠ACB = 55° (Angles opposite to equal sides in a triangle are equal)

In △ABD,

By angle sum property of triangle,

⇒ ∠ABD + ∠BDA + ∠BAD = 180°

⇒ 55° + 75° + ∠BAD = 180°

⇒ 130° + ∠BAD = 180°

⇒ ∠BAD = 180° - 130°

⇒ ∠BAD = 50°.

In △ABC,

By angle sum property of triangle,

⇒ ∠ABC + ∠ACB + ∠BAC = 180°

⇒ 55° + 55° + ∠BAD + ∠CAD = 180°

⇒ 55° + 55° + 50° + x° = 180°

⇒ 160° + x° = 180°

⇒ x° = 180° - 160°

⇒ x° = 20°

⇒ x = 20.

Hence, value of x = 20.

In each of the following figures, find the value of x :

(i)

(ii)

Answer

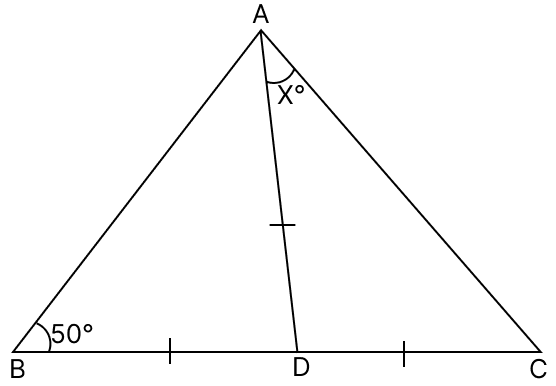
(i) In △ABD,

AD = BD

⇒ ∠ABD = ∠BAD = 50° (Angles opposite to equal sides in a triangle are equal)

By angle sum property of triangle,

⇒ ∠ABD + ∠BAD + ∠BDA = 180°

⇒ 50° + 50° + ∠BDA = 180°

⇒ 100° + ∠BDA = 180°

⇒ ∠BDA = 180° - 100°

⇒ ∠BDA = 80°.

In △ADC,

AD = CD

⇒ ∠DAC = ∠DCA = x° (Angles opposite to equal side in a triangle are equal)

⇒ ∠BDA + ∠CDA = 180° (Linear pair)

⇒ 80° + ∠CDA = 180°

⇒ ∠CDA = 180° - 80°

⇒ ∠CDA = 100°

By angle sum property of triangle,

⇒ ∠DAC + ∠DCA + ∠CDA = 180°

⇒ x° + x° + 100° = 180°

⇒ 2x° = 180° - 100°

⇒ 2x° = 80°

⇒ x° = $\dfrac{80°}{2}$

⇒ x° = 40°

⇒ x = 40.

Hence, the value of x = 40.

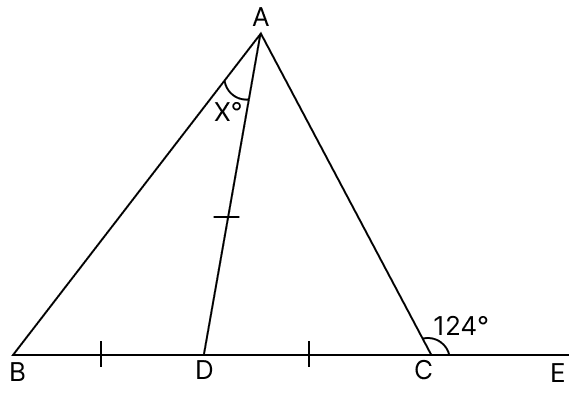
(ii) From figure,

⇒ ∠ACE + ∠ACD = 180°

⇒ 124° + ∠ACD = 180°

⇒ ∠ACD = 180° - 124°

⇒ ∠ACD = 56°.

In △ADC,

AD = CD

⇒ ∠DAC = ∠ACD = 56° (Angles opposite to equal sides in a triangle are equal)

By angle sum property of triangle,

⇒ ∠DAC + ∠ACD + ∠CDA = 180°

⇒ 56° + 56° + ∠CDA = 180°

⇒ 112° + ∠CDA = 180°

⇒ ∠CDA = 180° - 112°

⇒ ∠CDA = 68°.

From figure,

⇒ ∠CDA + ∠BDA = 180° (Linear pair)

⇒ 68° + ∠BDA = 180°

⇒ ∠BDA = 180° - 68°

⇒ ∠BDA = 112°.

In △ABD,

AD = BD

⇒ ∠DBA = ∠BAD = x° (Angles opposite to equal sides in a triangle are equal)

By angle sum property of triangle,

⇒ ∠DBA + ∠BAD + ∠BDA = 180°

⇒ x° + x° + 112° = 180°

⇒ 2x° = 180° - 112°

⇒ 2x° = 68°

⇒ x° = $\dfrac{68°}{2}$

⇒ x° = 34°

⇒ x = 34.

Hence, the value of x = 34.

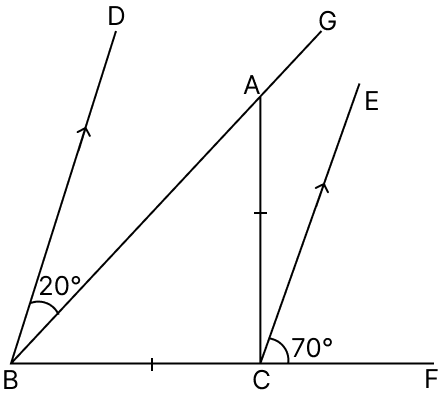
In the given figure, BD || CE; AC = BC, ∠ABD = 20° and ∠ECF = 70°. Find ∠GAC.

Answer

From figure,

BF is the transversal on parallel lines BD and CE.

⇒ ∠DBC = ∠ECF = 70° (Corresponding angles are equal)

⇒ ∠DBC = 70°

⇒ ∠DBA + ∠ABC = 70°

⇒ 20° + ∠ABC = 70°

⇒ ∠ABC = 70° - 20°

⇒ ∠ABC = 50°.

In △ABC,

AC = BC

⇒ ∠ABC = ∠BAC = 50° (Angles opposite to equal sides in a triangle are equal)

⇒ ∠BAC + ∠GAC = 180° (Linear pair)

⇒ 50° + ∠GAC = 180°

⇒ ∠GAC = 180° - 50°

⇒ ∠GAC = 130°.

Hence, ∠GAC = 130°.

In the given figure, AB = AC; ∠A = 50° and ∠ACD = 15°. Show that BC = CD.

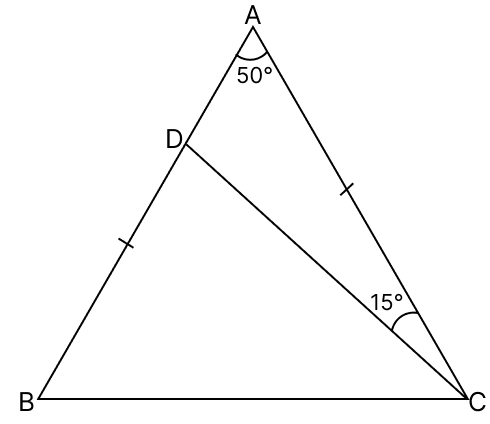
Answer

In △ACD,

By angle sum property of triangle,

⇒ ∠ACD + ∠CDA + ∠DAC = 180°

⇒ 15° + ∠CDA + 50° = 180°

⇒ ∠CDA + 65° = 180°

⇒ ∠CDA = 180° - 65°

⇒ ∠CDA = 115°.

From figure,

⇒ ∠CDA + ∠BDC = 180° (Linear pair)

⇒ 115° + ∠BDC = 180°

⇒ ∠BDC = 180° - 115°

⇒ ∠BDC = 65° .....(1)

In △ABC,

AB = BC

⇒ ∠ABC = ∠ACB = x° (Angles opposite to equal sides in a triangle are equal)

By angle sum property of triangle,

⇒ ∠ABC + ∠ACB + ∠BAC = 180°

⇒ x° + x° + 50° = 180°

⇒ 2x° = 180° - 50°

⇒ 2x° = 130°

⇒ x° = $\dfrac{130°}{2}$

⇒ x° = 65°

⇒ ∠ABC = ∠ACB = 65° ....(2)

From eq.(1) and (2), we have :

⇒ ∠BDC = ∠ABC = 65°

Since,

⇒ ∠DBC = ∠ABC

Thus,

⇒ ∠DBC = ∠BDC

Thus, in triangle DBC,

⇒ BC = CD (Sides opposite to equal angles in a triangle are equal)

Hence, proved that BC = CD.

In the given figure, AB || CD and CA = CE. Find the values of x, y and z.

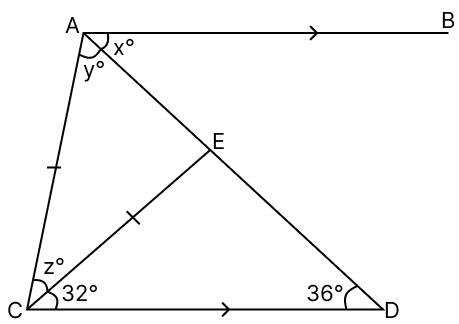
Answer

In △CED,

By angle sum property of triangle,

⇒ ∠ECD + ∠CDE + ∠DEC = 180°

⇒ 32° + 36° + ∠DEC = 180°

⇒ 68° + ∠DEC = 180°

⇒ ∠DEC = 180° - 68°

⇒ ∠DEC = 112°.

From figure,

⇒ ∠DEC + ∠AEC = 180° (Linear pair)

⇒ 112° + ∠AEC = 180°

⇒ ∠AEC = 180° - 112°

⇒ ∠AEC = 68°.

Given,

CA = CE

⇒ ∠EAC = ∠AEC = y° = 68° (Angles opposite to equal sides in a triangle are equal)

⇒ y = 68.

In △CEA,

By angle sum property of triangle,

⇒ ∠EAC + ∠AEC + ∠ECA = 180°

⇒ 68° + 68° + z° = 180°

⇒ 136° + z° = 180°

⇒ z° = 180° - 136°

⇒ z° = 44°

⇒ z = 44.

From figure,

∠BAD = ∠ADC (ALternate pair of angles between parallel lines AB and CD)

⇒ x° = 36°

⇒ x = 36.

Hence, the values of x = 36, y = 68 and z = 44.

If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.

Answer

Let ABC be an isosceles triangle with AB = AC.

Base BC is produced at points E, D respectively.

AB = AC

⇒ ∠ABC = ∠ACB = x (let) (Angles opposite to equal sides in a triangle are equal)

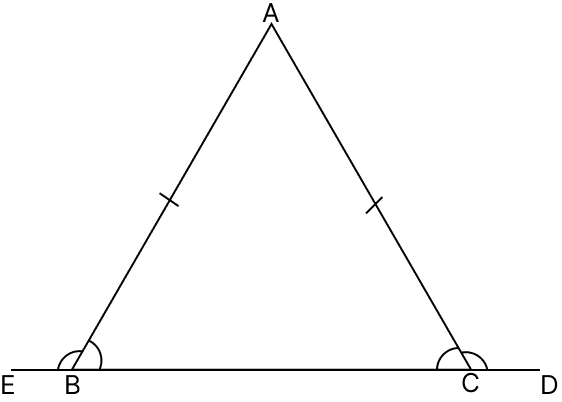
From figure,

⇒ ∠ACD + ∠ACB = 180° (Linear pair)

⇒ ∠ACD + x = 180°

⇒ ∠ACD = 180° - x ....(1)

From figure,

⇒ ∠ABE + ∠ABC = 180° (Linear pair)

⇒ ∠ABE + x = 180°

⇒ ∠ABE = 180° - x ....(2)

From eq.(1) and (2), we have:

⇒ ∠ABE = ∠ACD

Hence, proved that the exterior angles so formed are equal to each other.

In the given figure, side CA of △ABC has been produced to E. If AC = AD = BD; ∠ACD = 46° and ∠BAE = x°; find the value of x.

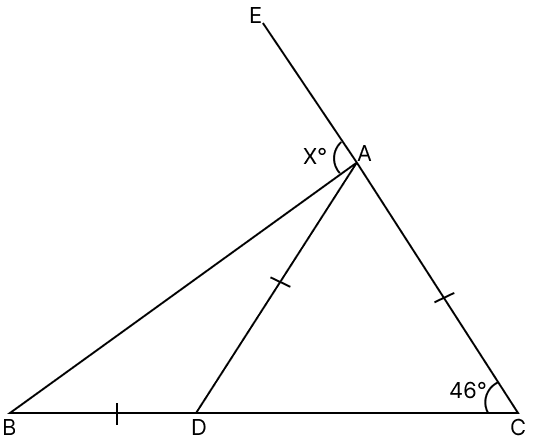
Answer

Given,

AD = AC

In △ADC,

⇒ ∠ACD = ∠ADC = 46° (Angles opposite to equal sides in a triangle are equal)

By angle sum property of triangle,

⇒ ∠ACD + ∠ADC + ∠CAD = 180°

⇒ 46° + 46° + ∠CAD = 180°

⇒ 92° + ∠CAD = 180°

⇒ ∠CAD = 180° - 92°

⇒ ∠CAD = 88°.

From figure,

⇒ ∠ADB + ∠ADC = 180° (Linear pair)

⇒ ∠ADB + 46° = 180°

⇒ ∠ADB = 180° - 46°

⇒ ∠ADB = 134°.

In △ABD,

AD = BD

⇒ ∠DAB = ∠DBA = z (let) (Angles opposite to equal sides are equal)

By angle sum property of triangle,

⇒ ∠ADB + ∠DAB + ∠DBA = 180°

⇒ 134° + z + z = 180°

⇒ 2z = 180° - 134°

⇒ 2z = 46°

⇒ z = $\dfrac{46°}{2}$

⇒ z = 23°.

⇒ ∠DAB = ∠DBA = 23°

From figure,

⇒ ∠CAD + ∠DAB + ∠BAE = 180° (Linear pair)

⇒ 88° + 23° + x° = 180°

⇒ 111° + x° = 180°

⇒ x° = 180° - 111°

⇒ x° = 69°

⇒ x = 69.

Hence, the value of x = 69.

In the given figure, CA = CD = BD; ∠DBC = 35° and ∠DCA = x°. Find the value of x.

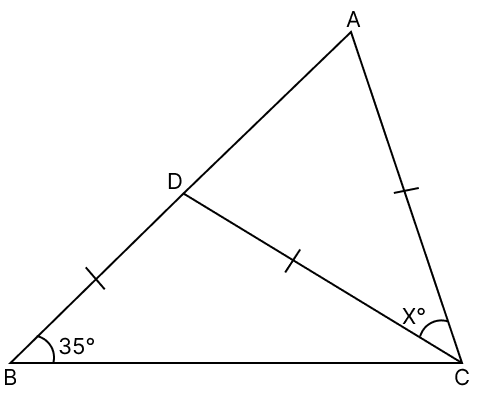
Answer

In △BDC,

BD = CD

⇒ ∠DBC = ∠DCB = 35° (Angles opposite to equal sides in a triangle are equal)

By angle sum property of triangle,

⇒ ∠DBC + ∠DCB + ∠BDC = 180°

⇒ 35° + 35° + ∠BDC = 180°

⇒ 70° + ∠BDC = 180°

⇒ ∠BDC = 180° - 70°

⇒ ∠BDC = 110°.

From figure,

⇒ ∠BDC + ∠ADC = 180° (Linear pair)

⇒ 110° + ∠ADC = 180°

⇒ ∠ADC = 180° - 110°

⇒ ∠ADC = 70°

In △ADC,

CA = CD

⇒ ∠ADC = ∠CAD = 70° (Angles opposite to equal sides are equal)

By angle sum property of triangle,

⇒ ∠ADC + ∠CAD + ∠ACD = 180°

⇒ 70° + 70° + x° = 180°

⇒ 140° + x° = 180°

⇒ x° = 180° - 140°

⇒ x° = 40°

⇒ x = 40.

Hence, the value of x = 40.

In the given figure, △ABC is an equilateral triangle whose base BC is produced to D such that BC = CD. Calculate :

(i) ∠ACD

(ii) ∠ADC

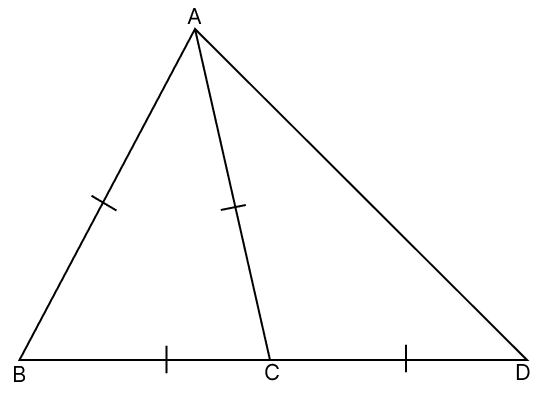
Answer

(i) Given, △ABC is an equilateral triangle.

∠BAC = ∠ACB = ∠ABC = 60°

From figure,

⇒ ∠ACB + ∠ACD = 180° (Linear pair)

⇒ 60° + ∠ACD = 180°

⇒ ∠ACD = 180° - 60°

⇒ ∠ACD = 120°.

Hence, ∠ACD = 120°.

(ii) In △ACD,

AC = CD

⇒ ∠CAD = ∠ADC = x (let) (Angles opposite to equal sides in a triangle are equal)

By angle sum property of triangle,

⇒ ∠CAD + ∠ADC + ∠ACD = 180°

⇒ x + x + 120° = 180°

⇒ 2x = 180° - 120°

⇒ 2x = 60°

⇒ x = $\dfrac{60°}{2}$

⇒ x = 30°

⇒ ∠CAD = ∠ADC = 30°.

Hence, ∠ADC = 30°.

In the given figure, AB = AD; CB = CD; ∠A = 42° and ∠C = 108°, find ∠ABC.

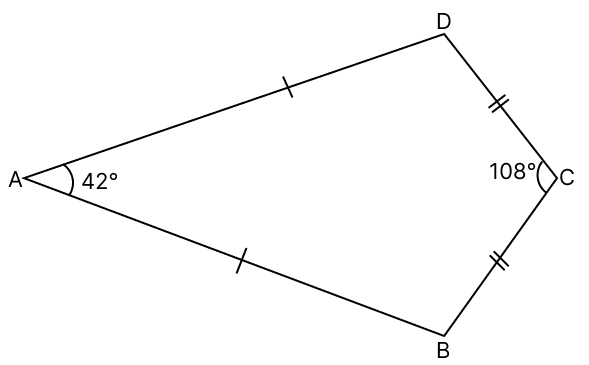
Answer

Join BD.

In △ABD,

AB = AD

⇒ ∠ABD = ∠ADB = x (let) (Angles opposite to equal sides in a triangle are equal)

By angle sum property of triangle,

⇒ ∠BAD + ∠ABD + ∠ADB = 180°

⇒ 42° + x + x = 180°

⇒ 2x = 180° - 42°

⇒ 2x = 138°

⇒ x = $\dfrac{138°}{2}$

⇒ x = 69°

⇒ ∠ABD = ∠ADB = 69°.

In △BCD,

CB = CD

⇒ ∠CBD = ∠CDB = y (let) (Angles opposite to equal sides in a triangle are equal)

By angle sum property of triangle,

⇒ ∠BCD + ∠CBD + ∠CDB = 180°

⇒ 108° + y + y = 180°

⇒ 2y = 180° - 108°

⇒ 2y = 72°

⇒ y = $\dfrac{72°}{2}$

⇒ y = 36°

⇒ ∠CBD = ∠CDB = 36°

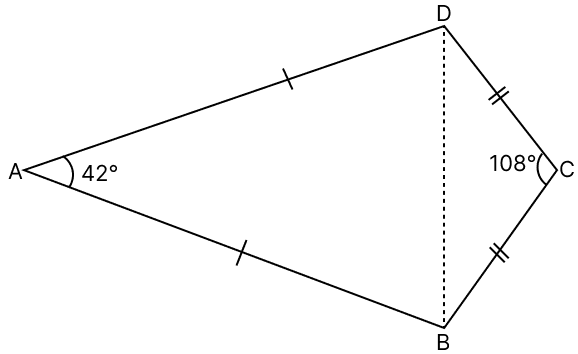
From figure,

∠ABC = ∠ABD + ∠CBD = 69° + 36° = 105°.

Hence, ∠ABC = 105°.

In the given figure, side BA of △ABC has been produced to D such that CD = CA and side CB has been produced to E. If ∠BAC = 106° and ∠ABE = 128°, find ∠BCD.

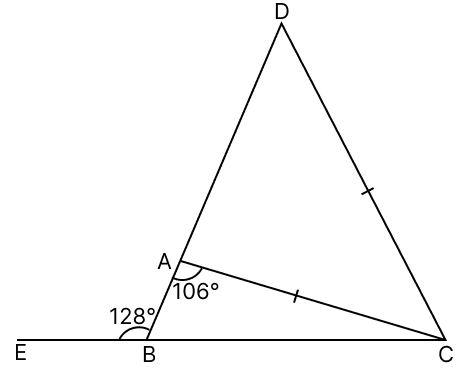
Answer

From figure,

⇒ ∠ABE + ∠ABC = 180° (Linear pair)

⇒ 128° + ∠ABC = 180°

⇒ ∠ABC = 180° - 128°

⇒ ∠ABC = 52°

In △ABC,

By angle sum property of triangle,

⇒ ∠ABC + ∠BAC + ∠ACB = 180°

⇒ 52° + 106° + ∠ACB = 180°

⇒ 158° + ∠ACB = 180°

⇒ ∠ACB = 180° - 158°

⇒ ∠ACB = 22°.

From figure,

⇒ ∠BAC + ∠CAD = 180° (Linear pair)

⇒ 106° + ∠CAD = 180°

⇒ ∠CAD = 180° - 106°

⇒ ∠CAD = 74°.

Given,

CD = CA

⇒ ∠CAD = ∠CDA = 74° (Angles opposite to equal sides in a triangle are equal)

In triangle CAD,

By angle sum property of triangle,

⇒ ∠ACD + ∠CAD + ∠CDA = 180°

⇒ ∠ACD + 74° + 74° = 180°

⇒ ∠ACD + 148° = 180°

⇒ ∠ACD = 180° - 148°

⇒ ∠ACD = 32°.

From figure,

∠BCD = ∠ACB + ∠ACD

= 22° + 32°

= 54°.

Hence, ∠BCD = 54°.

In the given figure, AB = BC and AC = CD. Show that: ∠BAD : ∠ADB = 3 : 1

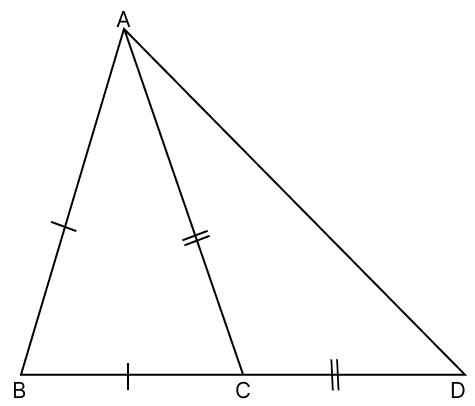
Answer

In △ABC,

AB = BC

⇒ ∠BAC = ∠ACB = x (let) (Angles opposite to equal sides in a triangle are equal)

In △ACD,

AC = CD

⇒ ∠CAD = ∠ADC = y (let) (Angles opposite to equal sides in a triangle are equal)

From figure,

⇒ ∠ACB + ∠ACD = 180° (Linear pair)

⇒ x + ∠ACD = 180°

⇒ ∠ACD = 180° - x

In △ACD,

By angle sum property of triangle,

⇒ ∠CAD + ∠ADC + ∠ACD = 180°

⇒ y + y + (180° - x) = 180°

⇒ 2y + 180° - x = 180°

⇒ 2y - x = 0

⇒ 2y = x

From figure,

∠BAD = ∠BAC + ∠CAD

⇒ ∠BAD = x + y

⇒ ∠BAD = 2y + y

⇒ ∠BAD = 3y

⇒ ∠BAD = 3∠ADC

From figure,

⇒ ∠ADC = ∠ADB

Thus,

⇒ ∠BAD = 3∠ADB

⇒ $\dfrac{\text{∠BAD}}{\text{∠ADB}} = \dfrac{3}{1}$

Hence, proved that ∠BAD : ∠ADB = 3 : 1.

Show that the perpendiculars drawn from the extremities of the base of an isosceles triangle to the opposite sides are equal.

Answer

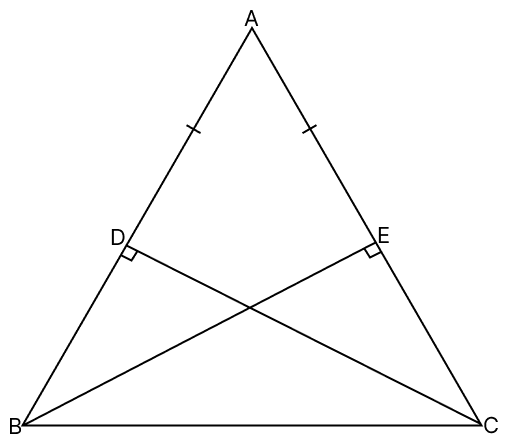
Let ABC be an isosceles triangle with AB = AC.

CD and BE are perpendiculars drawn from extremities of base BC.

In △ADC and △AEB,

⇒ AC = AB (Given)

⇒ ∠AEB = ∠ADC (Both equal to 90°)

⇒ ∠A = ∠A (Common angle)

∴ △ADC ≅ △AEB (By A.A.S axiom)

⇒ BE = CD (Corresponding parts of congruent triangles are equal)

Hence, the perpendiculars drawn from the extremities of the base of an isosceles triangle to the opposite sides are equal.

In a △ABC, AB = AC. If the bisectors of ∠B and ∠C meet AC and AB at points D and E respectively, show that :

(i) △DBC ≅ △ECB

(ii) BD = CE

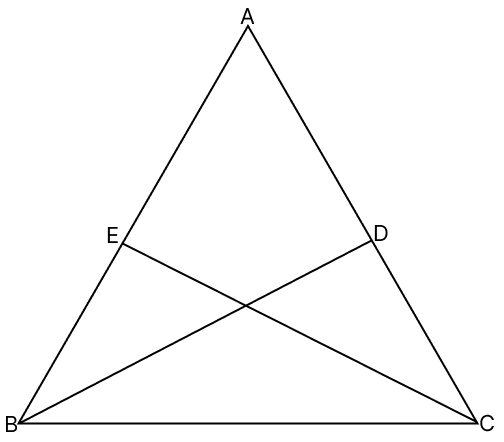
Answer

In △ABC,

AB = AC

⇒ ∠ABC = ∠ACB (Angles opposite to equal sides in a triangle are equal)

Given,

∠ABD = ∠DBC (DB is bisector of ∠B) ....(1)

∠ACE = ∠ECB (CE is bisector of ∠C) ....(2)

Since, ∠ABC = ∠ACB, from eq.(1) and (2), we have:

⇒ ∠ABD = ∠DBC = ∠ACE = ∠ECB

(i) In △ECB and △DBC,

⇒ BC = BC (Common side)

⇒ ∠ECB = ∠DBC (Proved above)

⇒ ∠EBC = ∠DCB (As, ∠ABC = ∠ACB)

∴ △ECB ≅ △DBC (By A.S.A. axiom)

Hence, proved that △ECB ≅ △DBC.

(ii) Since, △ECB ≅ △DBC

BD = CE (Corresponding parts of congruent triangles are equal)

Hence, proved that BD = CE.

In an isosceles triangle, prove that the altitude from the vertex bisects the base.

Answer

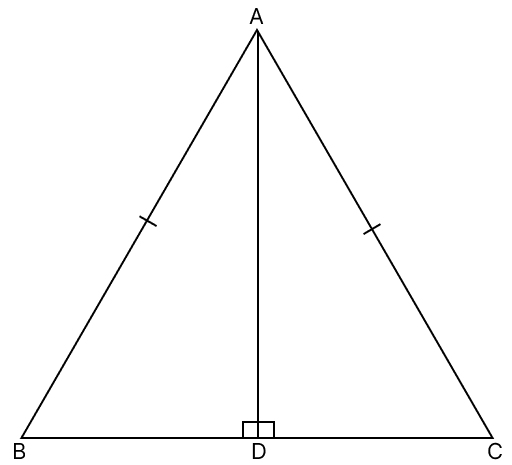
Let ABC be an isosceles triangle with AB = AC.

Let AD be a perpendicular from vertex A to base BC.

In △ADB and △ADC,

⇒ AD = AD (Common side)

⇒ AB = AC (Given)

⇒ ∠ADB = ∠ADC (Each equal to 90°)

∴ △ADB ≅ △ADC (By R.H.S axiom)

∴ DB = DC (Corresponding parts of congruent triangles are equal)

Hence, proved that the altitude from the vertex in an isosceles triangle bisects the base.

If the altitude from one vertex of a triangle bisects the opposite side, prove that the triangle is isosceles.

Answer

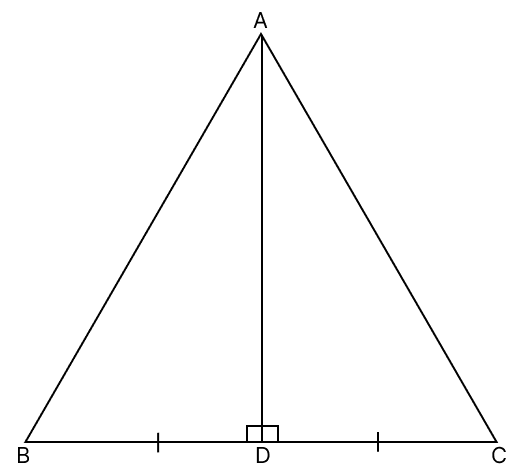
Let ABC be a triangle.

Let AD be a perpendicular from vertex A to base BC, which bisects it, i.e. DB = DC.

In △ADB and △ADC,

⇒ AD = AD (Common side)

⇒ BD = DC (Given)

⇒ ∠ADB = ∠ADC (Each equal to 90°)

∴ △ADB ≅ △ADC (By S.A.S. axiom)

∴ AB = AC (Corresponding parts of congruent triangles are equal)

∴ Triangle ABC is an isosceles triangle.

Hence, proved that the triangle is isosceles, if the altitude from one vertex of a triangle bisects the opposite side.

In the given figure, AD = AE and ∠BAD = ∠CAE. Prove that : AB = AC.

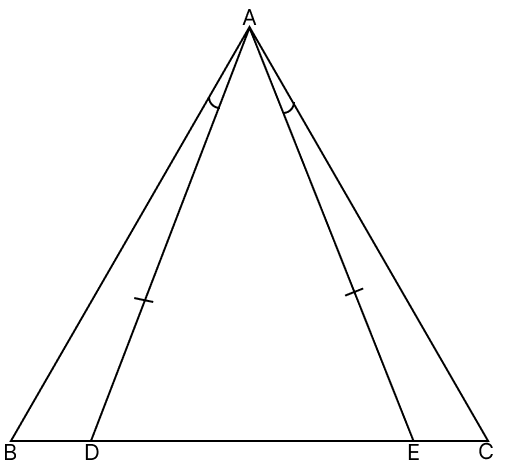
Answer

In △ADE,

AD = AE

⇒ ∠ADE = ∠AED (Angles opposite to equal sides in atriangle are equal)

From figure,

⇒ ∠ADE + ∠ADB = 180° (Linear pair)

⇒ ∠ADB = 180° - ∠ADE ....(1)

⇒ ∠AED + ∠AEC = 180° (Linear pair)

⇒ ∠AEC = 180° - ∠AED

⇒ ∠AEC = 180° - ∠ADE ....(2) (∵ ∠ADE = ∠AED)

From eq.(1) and (2), we have:

⇒ ∠AEC = ∠ADB

In △ABD and △ACE,

⇒ AD = AE (Given)

⇒ ∠ADB = ∠AEC (Proved above)

⇒ ∠BAD = ∠CAE (Given)

∴ △ABD ≅ △ACE (By A.S.A axiom)

⇒ AB = AC (Corresponding parts of congruent triangles are equal)

Hence, proved that AB = AC.

In the given figure, AB = AC; D is the mid-point of BC; DP ⊥ BA and DQ ⊥ CA. Prove that:

(i) DP = DQ

(ii) AP = AQ

(iii) AD bisects ∠A

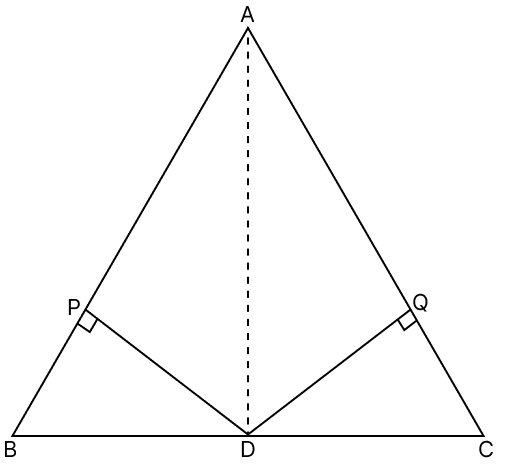
Answer

(i) In △ABC,

⇒ AB = AC (Given)

∴ ∠B = ∠C (Angles opposite to equal sides in a triangle are equal)

In △PDB and △QDC,

⇒ BD = CD (D is mid-point of BC)

⇒ ∠B = ∠C (Proved above)

⇒ ∠P = ∠Q (Both equal to 90°)

∴ △PDB ≅ △QDC (By A.A.S axiom)

⇒ DP = DQ (Corresponding parts of congruent triangles are equal)

Hence, proved that DP = DQ.

(ii) Since, △PDB ≅ △QDC

∴ BP = QC = y (let) (Corresponding parts of congruent triangles are equal)

⇒ AB = AC = x (let)

From figure,

⇒ AP = AB - BP = x - y ...(1)

⇒ AQ = AC - QC = x - y ...(2)

From eq.(1) and (2) we have :

∴ AP = AQ.

Hence, proved that AP = AQ.

(iii) In △ABD and △ACD,

⇒ AB = AC (Given)

⇒ BD = CD (Given)

⇒ AD = AD (Common side)

∴ △ABD ≅ △ACD (By S.S.S axiom)

⇒ ∠BAD = ∠CAD (Corresponding parts of congruent triangles are equal)

Hence, proved that AD bisects ∠A.

In the given figure, AB = AC. If BO and CO, the bisectors of ∠B and ∠C respectively meet at O and BC is produced to D, prove that ∠BOC = ∠ACD.

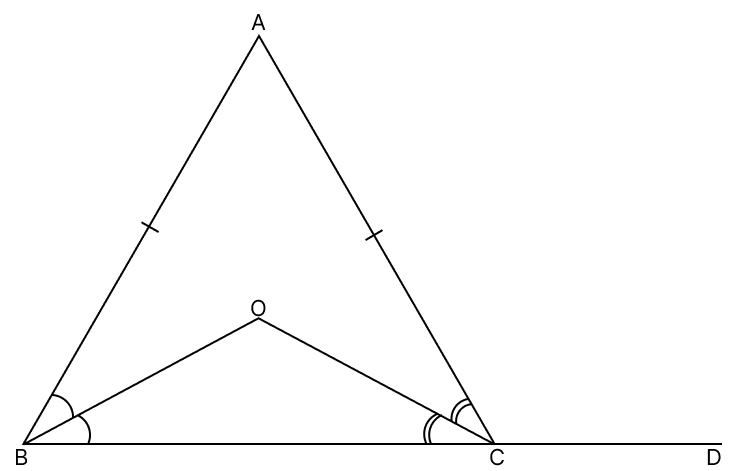
Answer

In △ABC,

AB = AC

⇒ ∠B = ∠C = x (let) (Angles opposite to equal sides in a triangle are equal)

From figure,

∠B = ∠ABO + ∠OBC

⇒ x = ∠OBC + ∠OBC (∵ ∠ABO = ∠OBC, as OB is the bisector of angle B)

⇒ x = 2∠OBC

⇒ ∠OBC = $\dfrac{\text{x}}{2}$ ....(1)

From figure,

∠C = ∠ACO + ∠OCB

⇒ x = ∠OCB + ∠OCB (∵ ∠ACO = ∠OCB, as OC is bisector of angle C)

⇒ x = 2∠OCB

⇒ ∠OCB = $\dfrac{\text{x}}{2}$ ....(2)

From eq.(1) and (2), we have :

⇒ ∠OCB = ∠OBC

In △BOC,

By angle sum property of triangle,

⇒ ∠OCB + ∠OBC + ∠BOC = 180°

⇒ $\dfrac{\text{x}}{2} + \dfrac{\text{x}}{2}$ + ∠BOC = 180°

⇒ x + ∠BOC = 180°

⇒ ∠BOC = 180° - x ....(3)

From figure,

⇒ ∠ACB + ∠ACD = 180° (Linear pair)

⇒ ∠ACO + ∠OCB + ∠ACD = 180°

⇒ $\dfrac{\text{x}}{2} + \dfrac{\text{x}}{2}$ + ∠ACD = 180° (∵ ∠ACO = ∠OCB)

⇒ x + ∠ACD = 180°

⇒ ∠ACD = 180° - x ....(4)

From eq.(3) and (4), we have:

⇒ ∠BOC = ∠ACD

Hence, proved that ∠BOC = ∠ACD.

Prove that the bisectors of the base angles of an isosceles triangle are equal.

Answer

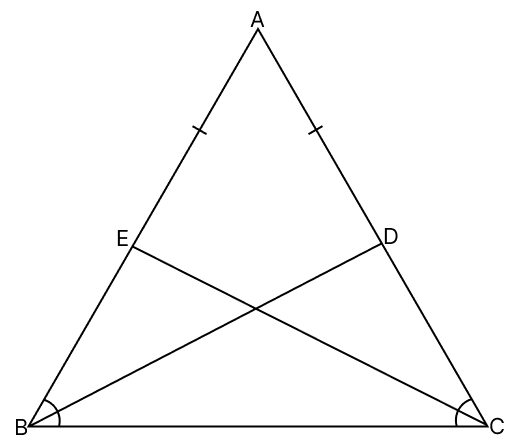
Let ABC be an isosceles triangle with AB = AC.

⇒ ∠B = ∠C (Angles opposite to equal sides in a triangle are equal)

CE and BD are the bisectors of angles ∠C and ∠B respectively to sides AB and AC respectively.

⇒ ∠ABD = ∠DBC and ∠ACE = ∠ECB

Since, angles B and C are equal, thus their half will also be equal.

⇒ ∠ABD = ∠DBC = ∠ACE = ∠ECB

In △AEC and △ADB,

⇒ AC = AB (Given)

⇒ ∠A = ∠A (Common angle)

⇒ ∠ACE = ∠ABD (Proved above)

∴ △AEC ≅ △ADB (By A.S.A axiom)

⇒ CE = BD (Corresponding parts of congruent triangles are equal.)

Hence, the bisectors of the base angles of an isosceles triangle are equal.

In the given figure, AB = AC and side BA has been produced to D. If AE is the bisector of ∠CAD, prove that AE || BC

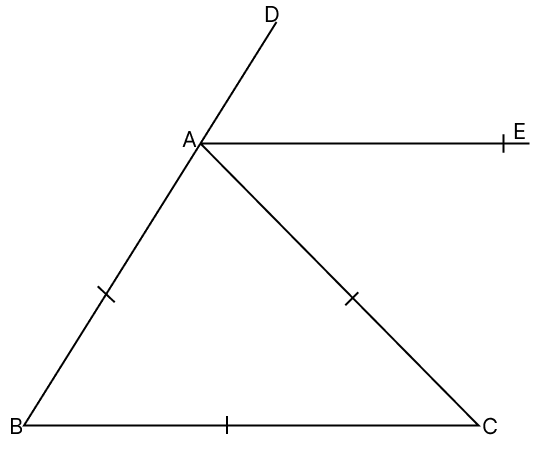
Answer

From figure,

△ABC is an equilateral triangle.

⇒ ∠BAC = ∠ACB = ∠ABC = 60°

Given,

AE is the bisector of ∠CAD

⇒ ∠CAE = ∠DAE = x (let)

From figure,

⇒ ∠BAC + ∠DAE + ∠CAE = 180° (Linear pair)

⇒ 60° + x + x = 180°

⇒ 2x = 180° - 60°

⇒ 2x = 120°

⇒ x = $\dfrac{120°}{2}$

⇒ x = 60°

⇒ ∠CAE = ∠DAE = 60°

∴ ∠CAE = ∠ACB = 60°

From figure,

∠CAE and ∠ACB are alternate angles between lines BC and AE and are equal.

Hence, proved that AE || BC.

In the given figure, AD is the internal bisector of ∠A and CE || DA. If CE meets BA produced at E, prove that △CAE is isosceles.

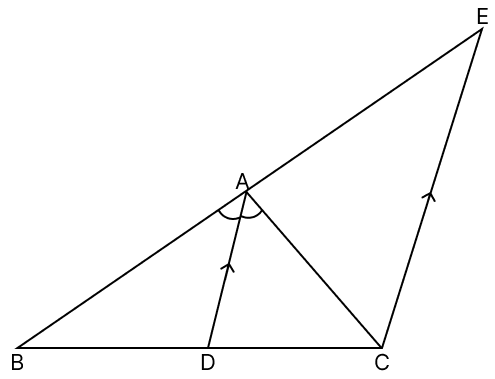
Answer

Given,

CE || AD

BE is the transversal.

From figure,

⇒ ∠DAC = ∠ACE ...(1) (Alternate angles are equal)

⇒ ∠BAD = ∠CEA (Corresponding angles are equal)

But, ∠BAD = ∠DAC (as AD is bisector of ∠BAC)

⇒ ∠DAC = ∠CEA ....(2)

From eq.(1) and (2), we have:

∴ ∠ACE = ∠CEA

AE = AC (Sides opposite to equal angles in a triangle are equal)

∴ △CAE is isosceles triangle.

Hence, proved that △CAE is isosceles.

In the adjoining figure, AB = AC. If DB ⊥ BC and EC ⊥ BC, prove that :

(i) BD = CE

(ii) AD = AE

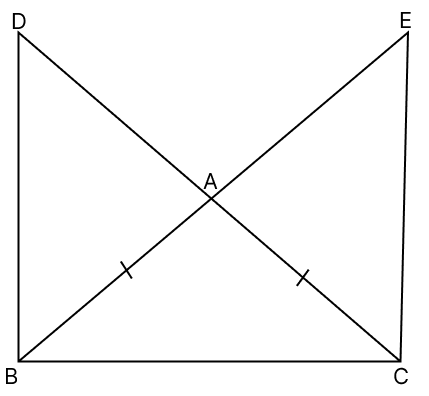
Answer

In △ABC,

AB = AC

⇒ ∠ABC = ∠ACB = x (let) (Angles opposite to equal sides in a triangle are equal)

Given, DB ⊥ BC, ∠DBC = 90°.

From figure,

⇒ ∠DBC = ∠DBA + ∠ABC

⇒ 90° = ∠DBA + x

⇒ ∠DBA = 90° - x .....(1)

Given, EC ⊥ BC, ∠ECB = 90°.

From figure,

⇒ ∠ECB = ∠ECA + ∠ACB

⇒ 90° = ∠ECA + x

⇒ ∠ECA = 90° - x .....(2)

From eq.(1) and (2), we have:

⇒ ∠DBA = ∠ECA

In △ABD and △ACE,

⇒ AB = AC (Given)

⇒ ∠DBA = ∠ECA (Proved above)

⇒ ∠DAB = ∠CAE (Vertically opposite angles are equal)

∴ △ABD ≅ △ACE (By A.S.A axiom)

(i) Since, △ABD ≅ △ACE

⇒ BD = CE (Corresponding parts of congruent triangles are equal)

Hence, proved that BD = CE.

(ii) Since, △ABD ≅ △ACE

⇒ AD = AE (Corresponding parts of congruent triangles are equal)

Hence, proved that AD = AE.

In the given figure, △ABC is an equilateral triangle and BC is produced to D such that BC = CD. Prove that AD ⊥ AB.

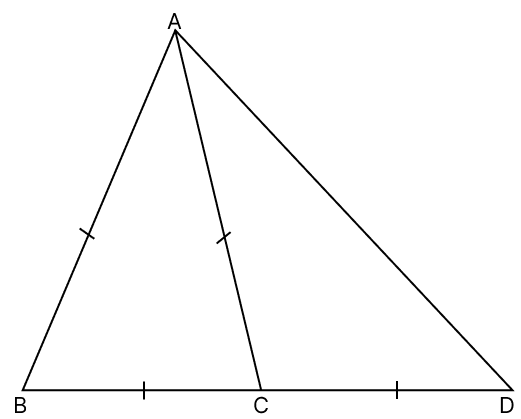
Answer

Given,

△ABC is an equilateral triangle.

⇒ ∠ABC = ∠ACB = ∠BAC = 60°

From figure,

⇒ ∠ACB + ∠ACD = 180° (Linear pair)

⇒ 60° + ∠ACD = 180°

⇒ ∠ACD = 180° - 60°

⇒ ∠ACD = 120°.

In △CAD,

CA = CD (As, BC = CD and BC = CA)

⇒ ∠CAD = ∠CDA = x (let) (Angles opposite to equal sides are equal)

By angle sum property of triangle,

⇒ ∠CAD + ∠CDA + ∠ACD = 180°

⇒ x + x + 120° = 180°

⇒ 2x = 180° - 120°

⇒ 2x = 60°

⇒ x = $\dfrac{60°}{2}$

⇒ x = 30°

⇒ ∠CAD = ∠CDA = 30°

From figure,

⇒ ∠BAD = ∠BAC + ∠CAD = 60° + 30° = 90°.

Hence, proved that AD ⊥ AB.

In the given figure, AC is the bisector of ∠A. If AB = AC, AD = CD and ∠ABC = 75°, find the values of x and y.

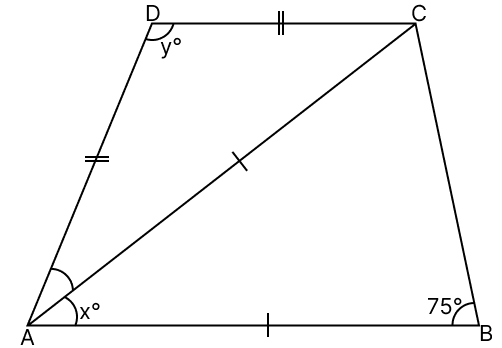
Answer

In △ABC,

AB = AC

⇒ ∠ABC = ∠ACB = 75° (Angles opposite to equal sides in a triangle are equal)

By angle sum property of triangle,

⇒ ∠ABC + ∠ACB + ∠BAC = 180°

⇒ 75° + 75° + x° = 180°

⇒ 150° + x° = 180°

⇒ x° = 180° - 150°

⇒ x° = 30°

⇒ x = 30.

Given,

AC is the bisector to ∠A

⇒ ∠DAC = ∠BAC = x° = 30°

In △ADC,

AD = CD

⇒ ∠DAC = ∠DCA = 30° (Angles opposite to equal sides are equal)

By angle sum property of triangle,

⇒ ∠DAC + ∠DCA + ∠ADC = 180°

⇒ 30° + 30° + y° = 180°

⇒ 60° + y° = 180°

⇒ y° = 180° - 60°

⇒ y° = 120°

⇒ y = 120.

Hence, the values of x = 30 and y = 120.

In a △PQR, ∠P = 50° and ∠R = 70°. Name :

(i) the shortest side

(ii) the longest side of the triangle

Answer

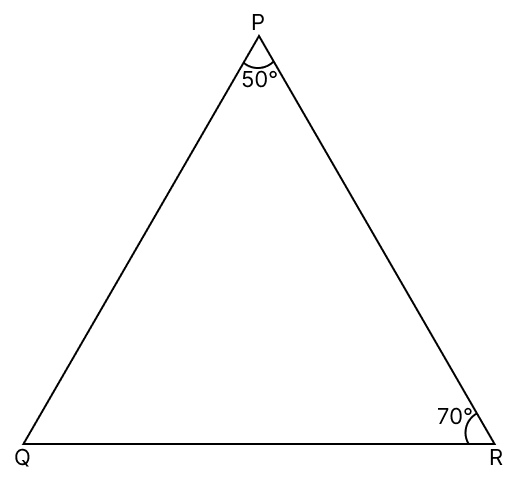
We know that,

Sum of angles of triangle = 180°

∴ ∠P + ∠Q + ∠R = 180°

⇒ 50° + ∠Q + 70° = 180°

⇒ ∠Q + 120° = 180°

⇒ ∠Q = 180° - 120°

⇒ ∠Q = 60°.

(i) We know that side opposite to the smallest angle is smallest side.

Since, P is the smallest angles,

∴ QR is shortest side of the triangle.

Hence, shortest side of the triangle PQR is QR.

(ii) We know that side opposite to the greatest angle is greatest side.

Since, R is the greatest angle,

∴ PQ is longest side of the triangle.

Hence, longest side of the triangle PQR is PQ.

In a △LMN, if ∠M = 90°, name the longest side of the triangle.

Answer

We know that,

Sum of angles of triangle = 180°

∴ ∠L + ∠M + ∠N = 180°

⇒ ∠L + 90° + ∠N = 180°

⇒ ∠L + ∠N = 180° - 90°

⇒ ∠L + ∠N = 90°

∴ ∠M > ∠L and ∠M > ∠N.

We know that side opposite to the greatest angle is greatest side.

∴ LN is longest side of the triangle.

Hence, LN is the longest side of the triangle.

In the given figure, side AB of △ABC is produced to D such that BD = BC. If ∠A = 60° and ∠B = 50°, prove that :

(i) AD > CD

(ii) AD > AC

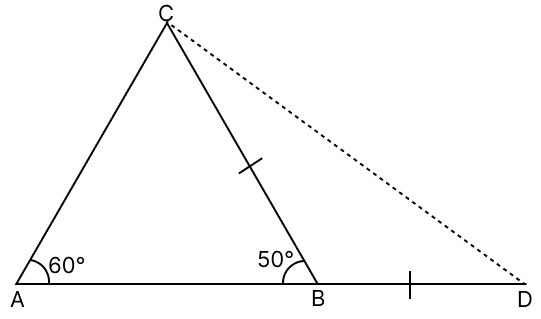
Answer

We know that,

Sum of angles of triangle = 180°

∴ ∠A + ∠B + ∠C = 180°

⇒ 60° + 50° + ∠C = 180°

⇒ 110° + ∠C = 180°

⇒ ∠C = 180° - 110°

⇒ ∠C = 70°.

From figure,

⇒ ∠CBD + ∠CBA = 180° (linear pair)

⇒ ∠CBD + 50° = 180°

⇒ ∠CBD = 180° - 50°

⇒ ∠CBD = 130°

In △BDC,

BD = BC

∴ ∠BDC = ∠BCD = x (let)

Sum of angles of triangle = 180°

∴ ∠BDC + ∠BCD + ∠CBD = 180°

⇒ x + x + 130° = 180°

⇒ 2x = 180° - 130°

⇒ 2x = 50°

⇒ x = $\dfrac{50°}{2}$

⇒ x = 25°

∴ ∠BDC = ∠BCD = 25°

From figure,

⇒ ∠ACD = ∠C + ∠BCD = 70° + 25° = 95°

(i) In △ADC,

We know that side opposite to the greatest angle is greatest side.

Since, ∠ACD is greatest,

∴ AD is longest side of the triangle.

⇒ AD > CD

Hence, proved that AD > CD.

(ii) Since, AD is greatest side of triangle ADC,

∴ AD > AC

Hence, proved that AD > AC.

In a right angled triangle, prove that the hypotenuse is the longest side.

Answer

Let LMN be a right angled triangle, ∠M = 90°

We know that,

Sum of angles of triangle = 180°

∴ ∠L + ∠M + ∠N = 180°

⇒ ∠L + 90° + ∠N = 180°

⇒ ∠L + ∠N = 180° - 90°

⇒ ∠L + ∠N = 90°

∴ ∠M > ∠L and ∠M > ∠N.

We know that, side opposite to the greatest angle is longest side.

∴ Hypotenuse LN, is the longest side of the triangle.

Hence, proved that hypotenuse is the longest side of the right angled triangle.

In the given figure, AB > AC. If BO and CO are the bisectors of ∠B and ∠C respectively, prove that BO > CO.

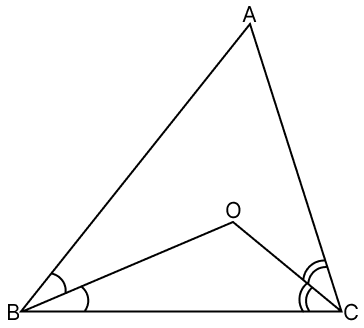
Answer

Given,

BO and CO are the bisectors of ∠B and ∠C respectively.

⇒ ∠ABO = ∠OBC and ∠ACO = ∠OCB

Given,

AB > AC

We know that angle opposite to the greater side is greater.

∴ ∠ACB > ∠ABC

⇒ ∠ACO + ∠OCB > ∠ABO + ∠OBC

⇒ ∠OCB + ∠OCB > ∠OBC + ∠OBC (∵ ∠ABO = ∠OBC and ∠ACO = ∠OCB)

⇒ 2∠OCB > 2∠OBC

⇒ ∠OCB > ∠OBC

In △BOC,

We know that side opposite to the greater angle is greater.

⇒ BO > CO.

Hence, proved that BO > CO.

In the given figure, sides AB and AC of △ABC have been produced to D and E respectively. If ∠CBD = x° and ∠BCE = y° such that x > y, show that AB > AC.

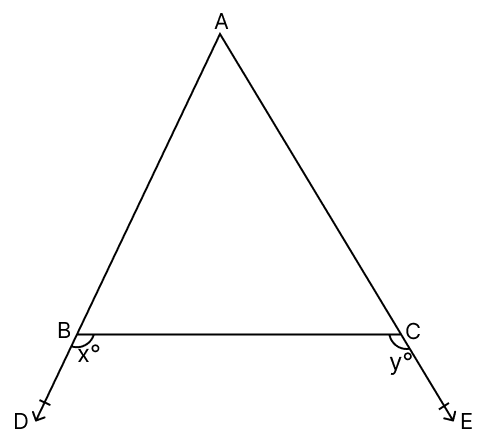
Answer

Given,

x > y

⇒ ∠CBD > ∠BCE

⇒ 180° - ∠CBD < 180° - ∠BCE

⇒ ∠ABC < ∠ACB

⇒ AC < AB (If two angles of a triangle are unequal, the greater angle has the greater side opposite to it)

⇒ AB > AC.

Hence, proved that AB > AC.

In the given figure, sides AB = AC. Show that AD > AB.

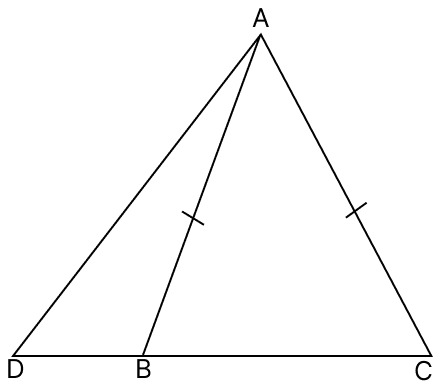
Answer

In △ABC,

⇒ ∠ABC = ∠ACB [As, AC = AB and angle opposite to equal sides are equal]

We know that,

In an isosceles triangle, the base angles are acute as only one obtuse angle can exist in a triangle.

∴ ∠ABC and ∠ACB are acute angles.

From figure,

DBC is a straight line.

⇒ ∠ABD + ∠ABC = 180° [Linear pair]

⇒ ∠ABD = 180° - ∠ABC

Since, ∠ABC is an acute angle thus, ∠ABD is an obtuse angle.

∴ In △ABD, ∠ABD is the largest angle.

∴ ∠ABD > ∠ADB

∴ AD > AB (If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.)

Hence, proved that AD > AB.

In the adjoining figure, AB > AC and D is any point on BC. Show that AB > AD

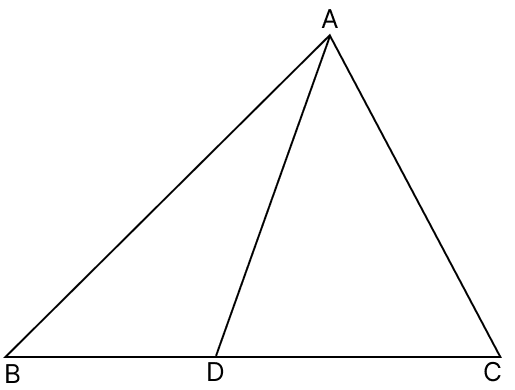
Answer

Given,

AB > AC

∴ ∠ACB > ∠ABC (As angle opposite to greater side is greater)

From figure,

∠ADB = ∠ACD + ∠DAC (As exterior angle is equal to sum of two opposite interior angles)

⇒ ∠ADB > ∠ACD

⇒ ∠ADB > ∠ACB

⇒ ∠ADB > ∠ABC [∵ ∠ACB > ∠ABC]

⇒ ∠ADB > ∠ABD

∴ AB > AD (As side opposite to greater angle is greater)

Hence, proved that AB > AD.

In the adjoining figure, AC > AB and AD is the bisector of ∠A. Show that : ∠ADC > ∠ADB

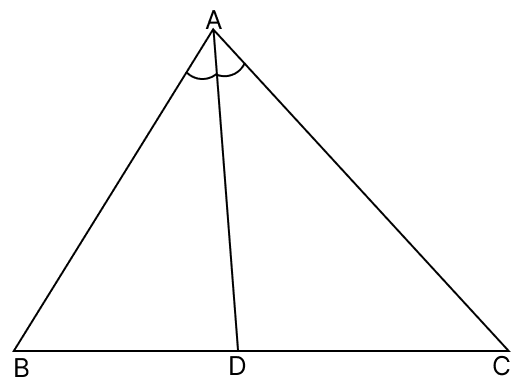
Answer

We know that,

In a triangle an exterior angle is equal to the sum of two opposite interior angles.

In △ADC,

⇒ ∠ADB = ∠CAD + ∠C .....(1)

In △ADB,

⇒ ∠ADC = ∠BAD + ∠B .....(2)

In △ABC,

⇒ AC > AB (Given)

⇒ ∠B > ∠C [If two sides of a triangle are unequal, the greater side has the greater angle opposite to it.]

Since, AD is the bisector of angle A.

∴ ∠BAD + ∠B > ∠CAD + ∠C ......(3)

From eq.(1), (2) and (3), we get:

⇒ ∠ADC > ∠ADB

Hence, proved that ∠ADC > ∠ADB.

In the adjoining figure, in △ABC, O is any point in its interior. Show that: OB + OC < AB + AC

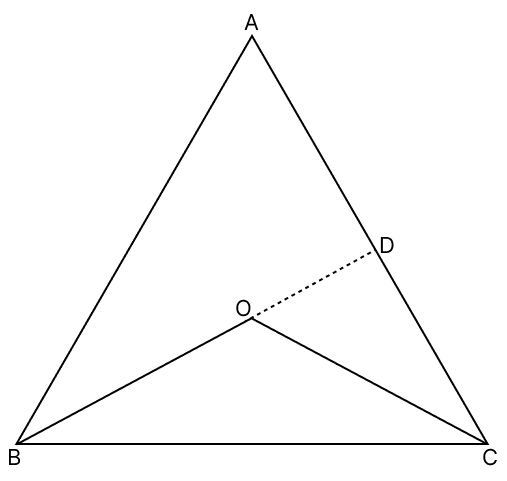
Answer

We know that,

In a triangle, sum of any two sides is always greater than the third side.

In △ABD,

⇒ AB + AD > BD

⇒ AB + AD > OB + OD .....(1)

In △COD,

⇒ OD + DC > OC .....(2)

Adding eq.(1) and (2), we have:

⇒ AB + AD + OD + DC > OB + OD + OC

⇒ AB + (AD + DC) > OB + OC

⇒ AB + AC > OB + OC

⇒ OB + OC < AB + AC.

Hence, proved that OB + OC < AB + AC.

In △ABC, D is any point on BC. Prove that : AB + BC + AC > 2 AD.

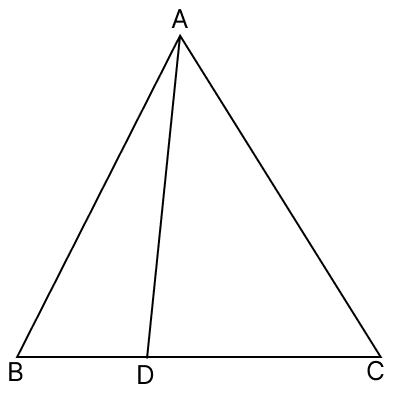
Answer

We know that,

In a triangle, sum of any two sides is always greater than the third side.

In △ABD,

⇒ AB + BD > AD .....(1)

In △ACD,

⇒ AC + CD > AD .....(2)

Adding eq.(1) and (2), we have :

⇒ AB + BD + AC + CD > AD + AD

⇒ AB + (BD + CD) + AC > 2AD

⇒ AB + BC + AC > 2AD.

Hence, proved that AB + BC + AC > 2AD.

In the adjoining figure, O is the centre of a circle, XY is a diameter and XZ is a chord. Prove that XY > XZ.

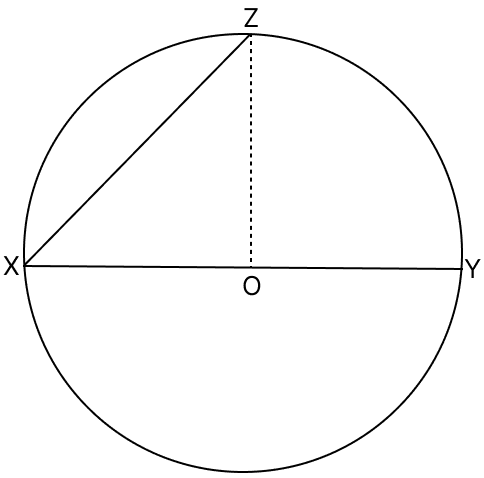
Answer

From figure,

OX = OZ = OY [Radius of same circle]

We know that,

In a triangle, sum of any two sides is always greater than the third side.

In △XOZ,

⇒ OX + OZ > XZ

⇒ OX + OY > XZ (∵ OZ = OY)

⇒ XY > XZ

Hence, proved that XY > XZ.

In the adjoining figure, PL ⊥ QR; LQ = LS and LR > LQ. Show that PR > PQ.

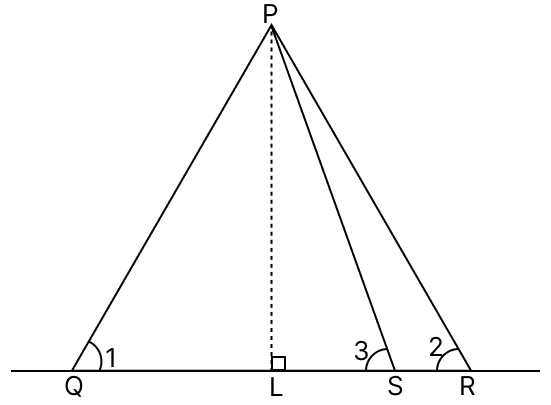
Answer

In △PLQ and △PLS,

LQ = LS (Given)

PL = PL (Common)

∠PLQ = ∠PLS (Both are equal to 90°)

△PLQ ≅ △PLS (By S.A.S axiom)

We know that corresponding parts of congruent triangles are equal.

∠1 = ∠3

In △PRS,

∠3 > ∠2 (As exterior angle is greater than each interior opposite angle)

∴ ∠1 > ∠2

⇒ PR > PQ (As side opposite to greater angle is greater)

Hence, proved that PR > PQ.

In the adjoining quadrilateral ABCD, AB is the longest side and DC is the shortest side. Prove that :

(i) ∠C > ∠A

(ii) ∠D > ∠B

Answer

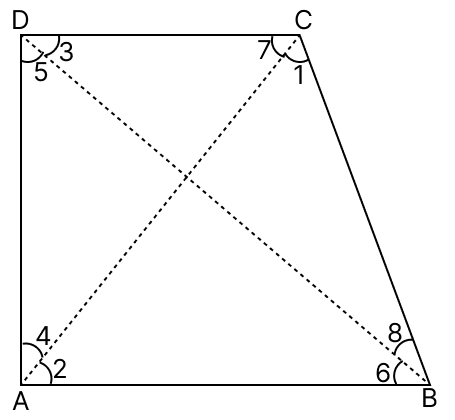
(i) Given,

In quadrilateral ABCD,

AB is the longest sides and DC is the shortest side.

Join BD and AC.

In △ABC,

⇒ AB > BC

∴ ∠1 > ∠2 .....(1) [If two sides of a triangle are unequal, the greater side has the greater angle opposite to it]

In △ADC,

⇒ AD > DC

∴ ∠7 > ∠4 .....(2) [If two sides of a triangle are unequal, the greater side has the greater angle opposite to it]

Adding eq.(1) and (2), we get:

⇒ ∠1 + ∠7 > ∠2 + ∠4

⇒ ∠C > ∠A

Hence, proved that ∠C > ∠A.

(ii) In △ABD,

⇒ AB > AD

∴ ∠5 > ∠6 .....(1) [If two sides of a triangle are unequal, the greater side has the greater angle opposite to it]

In △BDC,

⇒ BC > CD

∴ ∠3 > ∠8 .....(2) [If two sides of a triangle are unequal, the greater side has the greater angle opposite to it]

Adding eq.(1) and (2), we get:

⇒ ∠5 + ∠3 > ∠6 + ∠8

⇒ ∠D > ∠B

Hence, proved that ∠D > ∠B.

Can you construct a △ABC in which AB = 5 cm, BC = 4 cm and AC = 9 cm? Give reason.

Answer

Let ABC be the triangle.

AB = 5 cm, BC = 4 cm, AC = 9 cm.

We know that,

In a triangle, sum of any two sides is greater than the third side.

AB + BC = 5 + 4 = 9 cm is equal to third side AC = 9 cm.

Hence, we cannot construct a triangle using given sides.

In the adjoining figure, △ABC is equilateral and D is any point on AC. Prove that:

(i) BD > AD

(ii) BD > DC

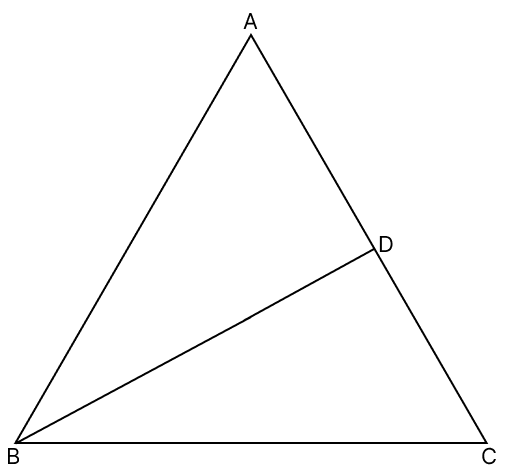
Answer

(i) Since, ABC is an equilateral triangle.

∴ ∠A = ∠B = ∠C = 60°

In △ ABD,

∠ABD = ∠B - ∠DBC

∴ ∠ABD < ∠B

∴ ∠ABD < ∠A (Since, ∠B = ∠A)

∴ AD < BD or BD > AD [If two angles of a triangle are unequal, the greater angle has the greater side opposite to it]

Hence, proved that BD > AD.

(ii) In △ BDC,

∠DBC = ∠B - ∠ABD

∴ ∠DBC < ∠B

∴ ∠DBC < ∠C (∵ ∠B = ∠C)

∴ DC < BD or BD > DC [If two angles of a triangle are unequal, the greater angle has the greater side opposite to it]

Hence, proved that BD > DC.

If O is any point inside △ABC, prove that ∠BOC > ∠A.

Answer

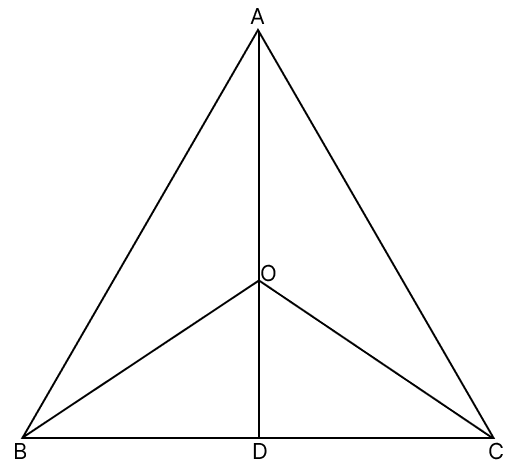
Join OA, OB and OC, produce OA to meet BC at D.

In △AOB,

∠BOD > ∠BAO .....(1) (Exterior angle is greater than interior opposite angle)

In △AOC,

∠COD > ∠CAO .....(2) (Exterior angle is greater than interior opposite angle)

Adding eq.(1) and (2), we have:

∠BOD + ∠COD > ∠BAO + ∠CAO

⇒ ∠BOC > ∠BAC

⇒ ∠BOC > ∠A.

Hence, proved that ∠BOC > ∠A.

In the given figure, AD = AB and AE bisects ∠A. Prove that:

(i) BE = ED

(ii) ∠ABD > ∠BCA

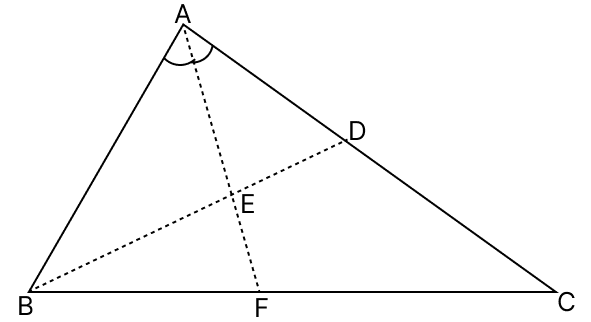
Answer

In △ABE and △ADE,

⇒ AE = AE (Common side)

⇒ AB = AD (Given)

⇒ ∠BAE = ∠DAE (∵ AE bisects ∠A)

∴ △ABE ≅ △ADE (By S.A.S axiom)

(i) Since, △ABE ≅ △ADE

We know that,

Corresponding parts of congruent triangle are equal.

∴ BE = ED

Hence, proved that BE = ED.

(ii) Since, △ABE ≅ △ADE

We know that,

Corresponding parts of congruent triangle are equal.

∴ ∠ABE = ∠ADE

⇒ ∠ABD = ∠ADB

From figure,

⇒ ∠BDA > ∠BCA (∵ Exterior angle is greater than interior opposite angle)

⇒ ∠ABD > ∠BCA

Hence, proved that ∠ABD > ∠BCA.

The sides AB and AC of △ABC are produced to D and E respectively and the bisectors of ∠CBD and ∠BCE meet at O. If AB > AC, prove that OC > OB.

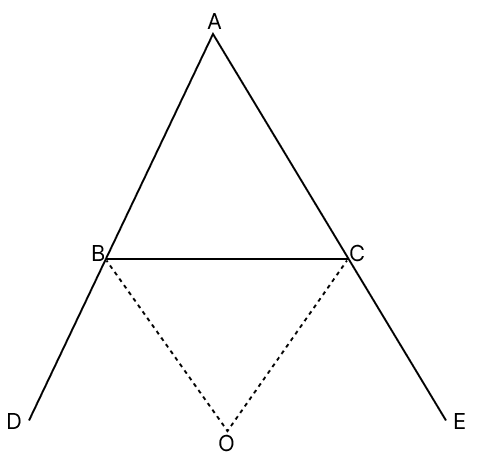
Answer

In △ABC,

AB > AC

⇒ ∠ACB > ∠ABC

∠ACB + ∠BCE = 180° .....(1) [Linear pair]

∠ABC + ∠CBD = 180° .....(2) [Linear pair]

Adding eq.(1) and (2), we have:

∠ACB + ∠BCE = ∠ABC + ∠CBD

Since, ∠ACB > ∠ABC

⇒ ∠BCE < ∠CBD

⇒ $\dfrac{1}{2}$ ∠BCE < $\dfrac{1}{2}$ ∠CBD

⇒ ∠BCO < ∠CBO

⇒ ∠CBO > ∠BCO

∴ OC > OB.

Hence, proved that OC > OB.

In △ABC, AB = 7.5 cm, BC = 6.2 cm and AC = 5.4 cm. Name :

(i) the least angle

(ii) the greatest angle of the triangle

Answer

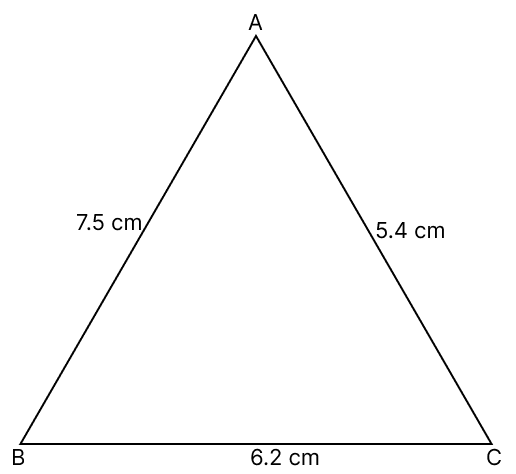
(i) In △ABC,

We know that,

The smallest side of a triangle has the smallest angle opposite to it.

Since, AC is the shortest side.

∴ ∠B is the least angle.

Hence, ∠B is the least angle.

(ii) In △ABC,

We know that,

The largest side of a triangle has the largest angle opposite to it.

Since, AB is the largest side.

∴ ∠C is the greatest angle.

Hence, ∠C is the greatest angle.

In the given figure, AD bisects ∠A. If ∠B = 60°, ∠C = 40°, then arrange AB, BD and DC in ascending order of their lengths.

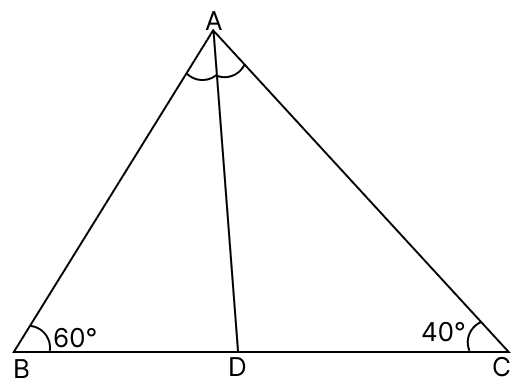
Answer

Given,

AD bisects ∠A.

⇒ ∠BAD = ∠CAD = x (let)

In △ABC,

By angle sum property of triangle,

⇒ ∠A + ∠B + ∠C = 180°

⇒ ∠A + 60° + 40° = 180°

⇒ ∠A + 100° = 180°

⇒ ∠A = 180° - 100°

⇒ ∠A = 80°

⇒ ∠BAD + ∠CAD = 80°

⇒ x + x = 80°

⇒ 2x = 80°

⇒ x = $\dfrac{80°}{2}$

⇒ x = 40°

⇒ ∠BAD = ∠CAD = 40°

In △ABD,

By angle sum property of triangle,

⇒ ∠BAD + ∠B + ∠ADB = 180°

⇒ 40° + 60° + ∠ADB = 180°

⇒ 100° + ∠ADB = 180°

⇒ ∠ADB = 180° - 100°

⇒ ∠ADB = 80°

We know that,

In a triangle larger angle has larger side opposite to it.

Since,

∠ADB > ∠ABD > ∠BAD

∴ AB > AD > BD .......(1)

From figure,

⇒ ∠ADB + ∠ADC = 180° (Linear pair)

⇒ 80° + ∠ADC = 180°

⇒ ∠ADC = 180° - 80°

⇒ ∠ADC = 100°

Since,

⇒ ∠DAC = ∠ACD (Both equal to 40°)

∴ AD = DC (Sides opposite to equal angles are equal)

Substituting value of AD in equation (1), we get :

⇒ AB > DC > BD

⇒ BD < DC < AB.

Hence, BD < DC < AB.

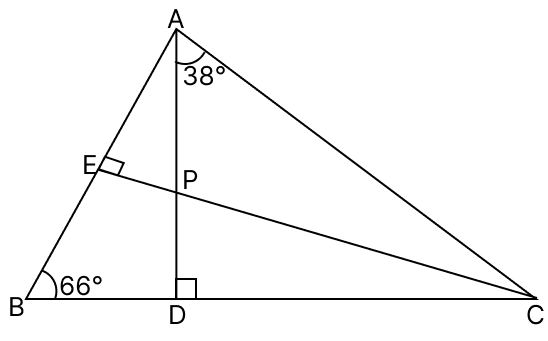
In the given figure, ∠ABC = 66°, ∠DAC = 38°. CE is perpendicular to AB and AD is perpendicular to BC. Prove that: CP > AP.

Answer

In △ABD,

By angle sum property of triangle,

⇒ ∠ABD + ∠ADB + ∠BAD = 180°

⇒ 66° + 90° + ∠BAD = 180°

⇒ ∠BAD + 156° = 180°

⇒ ∠BAD = 180° - 156°

⇒ ∠BAD = 24°

In △AEP,

By angle sum property of triangle,

⇒ ∠AEP + ∠APE + ∠BAD = 180°

⇒ 90° + ∠APE + 24° = 180°

⇒ ∠APE + 114° = 180°

⇒ ∠APE = 180° - 114°

⇒ ∠APE = 66°

From figure,

∠APE + ∠APC = 180° (Linear pair)

⇒ 66° + ∠APC = 180°

⇒ ∠APC = 180° - 66°

⇒ ∠APC = 114°

In △APC,

By angle sum property of triangle,

⇒ ∠APC + ∠ACP + ∠PAC = 180°

⇒ 114° + ∠ACP + 38° = 180°

⇒ ∠ACP + 152° = 180°

⇒ ∠ACP = 180° - 152°

⇒ ∠ACP = 28°

We know that,

The shortest side of a triangle has the shortest angle opposite to it.

⇒ AP < CP

⇒ CP > AP.

Hence, proved that CP > AP.

In a △ABC, AB = AC and ∠B = 50°. Then ∠A =

1. 50°

2. 80°

3. 100°

4. 105°

Answer

In △ABC,

AB = AC

⇒ ∠B = ∠C = 50° (Angles opposite to equal sides in a triangle are equal)

By angle sum property of triangle,

⇒ ∠A + ∠B + ∠C = 180°

⇒ ∠A + 50° + 50° = 180°

⇒ ∠A + 100° = 180°

⇒ ∠A = 180° - 100°

⇒ ∠A = 80°.

Hence, option 2 is the correct option.

In a △PQR, ∠Q = 50°, ∠R = 65° and QR = 4 cm. Then PQ =

1. 6 cm

2. 5 cm

3. 4 cm

4. 3 cm

Answer

In △PQR,

By angle sum property of triangle,

⇒ ∠P + ∠Q + ∠R = 180°

⇒ ∠P + 50° + 65° = 180°

⇒ ∠P + 115° = 180°

⇒ ∠P = 180° - 115°

⇒ ∠P = 65°

Since, ∠P = ∠R = 65°

⇒ PQ = QR = 4 cm (Sides opposite to equal angles in a triangle are equal)

Hence, option 3 is the correct option.

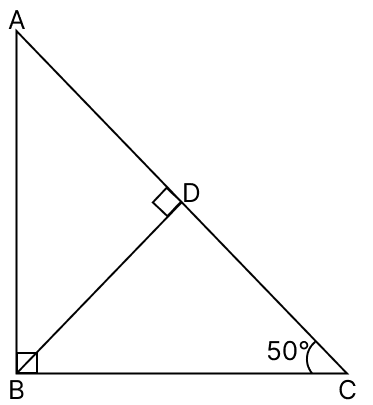
In the adjoining figure, ∠ABC = 90°, ∠BCA = 50° and BD ⊥ AC. Then ∠ABD =

1. 30°

2. 40°

3. 50°

4. 60°

Answer

In △ABC,

By angle sum property of triangle,

⇒ ∠A + ∠B + ∠C = 180°

⇒ ∠A + 90° + 50° = 180°

⇒ ∠A + 140° = 180°

⇒ ∠A = 180° - 140°

⇒ ∠A = 40°.

In △ABD,

By angle sum property of triangle,

⇒ ∠A + ∠ABD + ∠D = 180°

⇒ 40° + ∠ABD + 90° = 180°

⇒ ∠ABD + 130° = 180°

⇒ ∠ABD = 180° - 130°

⇒ ∠ABD = 50°.

Hence, option 3 is the correct option.

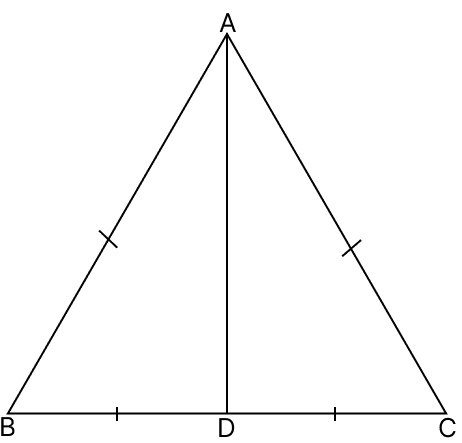
In the adjoining figure, AB = AC and BD = CD. Then, ∠ADC =

1. 60°

2. 75°

3. 90°

4. 100°

Answer

In △ABD and △ACD,

⇒ AD = AD (Common side)

⇒ BD = CD (Given)

⇒ AB = AC (Given)

∴ △ABD ≅ △ACD (By S.S.S axiom)

⇒ ∠ADB = ∠ADC = x (let) (Corresponding parts of congruent triangles are equal)

From figure,

⇒ ∠ADB + ∠ADC = 180° (Linear pair)

⇒ x + x = 180°

⇒ 2x = 180°

⇒ x = $\dfrac{180°}{2}$

⇒ x = 90°

⇒ ∠ADB = ∠ADC = 90°.

Hence, option 3 is the correct option.

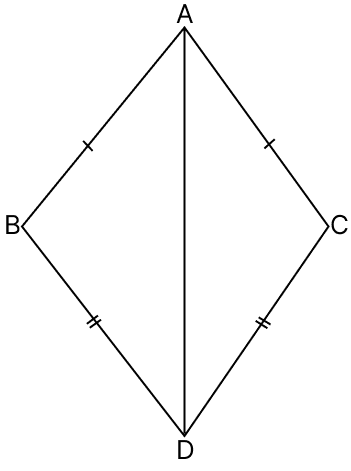
In the adjoining figure, AB = AC, BD = CD, ∠BAD = 32°, ∠BDC = 56°, ∠CAD = 2x° and ∠BDA = (x + y)°. The values of x and y will be :

1. x = 10, y = 16

2. x = 16, y = 12

3. x = 18, y = 8

4. x = 12, y = 16

Answer

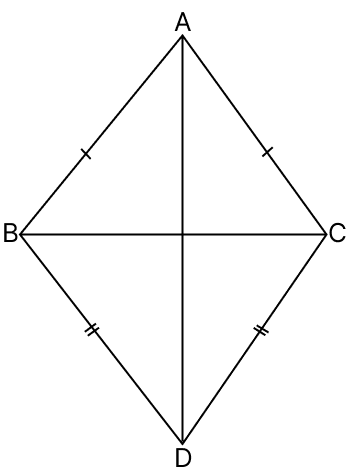
Join BC.

In △BDC,

BD = DC

∠DBC = ∠DCB = a (let)

∴ ∠DBC + ∠DCB + ∠BDC = 180°

⇒ a + a + 56° = 180°

⇒ 2a = 180° - 56°

⇒ 2a = 124°

⇒ a = $\dfrac{124°}{2}$

⇒ a = 62°

⇒ ∠DBC = ∠DCB = 62°

In △ABC,

AB = AC

∠ABC = ∠ACB

∠ABD = ∠ABC + ∠DBC ....(1)

∠ACD = ∠ACB + ∠DCB

⇒ ∠ACD = ∠ABC + ∠DBC ....(2)

From eq.(1) and (2), we have :

⇒ ∠ABD = ∠ACD

In △ABC,

∴ ∠A + ∠ABC + ∠ACB = 180°

⇒ ∠BAD + ∠CAD + ∠ABC + ∠ABC = 180°

⇒ 32° + 2x° + 2∠ABC = 180°

⇒ 2∠ABC = 180° - 32° - 2x°

⇒ 2∠ABC = 148° - 2x°

⇒ ∠ABC = 74° - x°

Substituting value of ∠ABC in eq.(1):

⇒ ∠ABD = ∠ABC + ∠DBC

⇒ ∠ABD = 74° - x° + 62°

⇒ ∠ABD = 136° - x°

In △ABD,

⇒ ∠ABD + ∠BAD + ∠BDA = 180°

⇒ 136° - x° + 32° + x° + y° = 180°

⇒ 168° + y° = 180°

⇒ y° = 180° - 168°

⇒ y° = 12°

⇒ y = 12.

In an isosceles triangle BDC,

BD = CD

We know that,

Perpendicular drawn from the vertex of an isosceles triangle bisects the base.

⇒ ∠DOB = ∠DOC = 90°

In △DOB,

⇒ ∠DBO + ∠DOB + ∠BDO = 180°

⇒ 62° + 90° + x° + y° = 180°

⇒ 152° + x° + 12° = 180°

⇒ 164° + x° = 180°

⇒ x° = 180° - 164°

⇒ x° = 16°

⇒ x = 16.

Hence, option 2 is the correct option.

In the figure, AB = AC and DB = DC. ∠ABD : ∠ACD is :

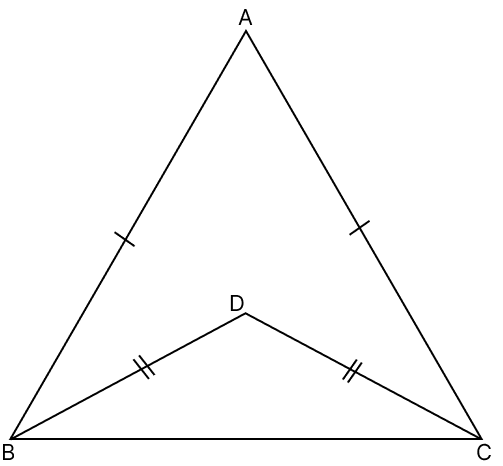
1. 1 : 2

2. 2 : 1

3. 1 : 1

4. 1 : 3

Answer

In △ABC,

AB = AC

⇒ ∠B = ∠C = x ....(1) (let) (Angles opposite to equal sides in a triangle are equal)

In △BDC,

BD = CD

⇒ ∠DBC = ∠DCB = y ....(2) (let) (Angles opposite to equal sides in a triangle are equal)

Subtracting eq.(2) from (1), we have :

⇒ ∠B - ∠DBC = ∠C - ∠DCB

⇒ ∠ABD = ∠ACD

⇒ ∠ABD : ∠ACD = 1 : 1.

Hence, option 3 is the correct option.

In right triangles ABC and DEF, if hypotenuse AB = EF and side AC = DE, then △ABC is congruent to:

1. △FED

2. △EFD

3. △DEF

4. △FDE

Answer

In △ABC and △EFD,

⇒ AB = EF (Given)

⇒ AC = DE (Given)

⇒ ∠C = ∠D (Both equal to 90°)

∴ △ABC ≅ △EFD (By R.H.S axiom)

Hence, option 2 is the correct option.

ABC is a right angled triangle whose hypotenuse is AC. If AB : BC = 3 : 4, then the smallest angle of the triangle is :

1. ∠A

2. ∠B

3. ∠C

4. None of these

Answer

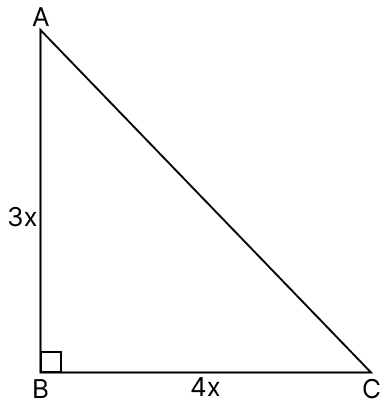
In △ABC,

Given,

AB : BC = 3 : 4

Let, AB = 3x and BC = 4x

By pythagoras theorem,

⇒ AC² = AB² + BC²

⇒ AC² = (3x)² + (4x)²

⇒ AC² = 9x² + 16x²

⇒ AC² = 25x²

⇒ AC = $\sqrt{25\text{x}^2}$

⇒ AC = 5x.

We know that,

The shortest angle of a triangle has the shortest side opposite to it.

Since, side AB is shortest, thus ∠C is the shortest angle.

Hence, option 3 is the correct option.

If a, b, c be the lengths of the sides of a triangle, then :

1. a = b + c

2. a < b + c

3. a > b + c

4. a < b - c

Answer

We know that,

The sum of lengths of any two sides of a triangle must be greater than the third side.

⇒ a < b + c

Hence, option 2 is the correct option.

In a △ABC, AB > BC > CA. Then :

1. AB - BC < CA

2. AB - BC > CA

3. AB + BC < CA

4. None of these

Answer

We know that,

Difference between any two sides of a triangle must be less than the third side.

In △ABC,

AB - BC < CA

Hence, option 1 is the correct option.

In a △ABC, ∠A = 40° and ∠B = 60°. The longest side of the triangle is:

1. AB

2. BC

3. CA

4. None of these

Answer

In △ABC,

By angle sum property of triangle,

⇒ ∠A + ∠B + ∠C = 180°

⇒ 40° + 60° + ∠C = 180°

⇒ ∠C + 100° = 180°

⇒ ∠C = 180° - 100°

⇒ ∠C = 80°

We know that,

The longest side of a triangle has the largest angle opposite to it.

Since, angle C is the greatest, thus AB is longest side of the triangle.

Hence, option 1 is the correct option.

In a △ABC, AB = 6 cm, BC = 7 cm and CA = 8 cm. The smallest angle of the triangle is :

1. ∠A

2. ∠B

3. ∠C

4. None of these

Answer

We know that,

The smallest angle of a triangle has the smallest side opposite to it.

Since, AB is the smallest side thus ∠C is the smallest angle of the triangle.

Hence, option 3 is the correct option.

In a △ABC, 2∠A = 3∠B and ∠C = 100°. The correct ascending order of sides of the triangle is :

1. AC < BC < AB

2. BC < AC < AB

3. AB < AC < AB

4. BC < AB < AC

Answer

Given,

2∠A = 3∠B

⇒ ∠A : ∠B = 3 : 2

⇒ ∠A = 3x° and ∠B = 2x°

In △ABC,

By angle sum property of triangle,

⇒ ∠A + ∠B + ∠C = 180°

⇒ 3x° + 2x° + 100° = 180°

⇒ 5x° = 180° - 100°

⇒ 5x° = 80°

⇒ x° = $\dfrac{80°}{5}$

⇒ x° = 16°

⇒ ∠A = 3x° = 3 × 16° = 48°

⇒ ∠B = 2x° = 2 × 16° = 32°

We know that,

The longest side of a triangle has the largest angle opposite to it.

Since, C is the largest angle, thus AB is longest side of the triangle.

The shortest side of a triangle has the smallest angle opposite to it.

Since, B is the smallest angle, thus AC is smallest side of the triangle.

∴ AC < BC < AB.

Hence, option 1 is the correct option.

The angles of a triangle are 5(x - 4)°, (4x + 5)° and (x + 25)°, then the value of x is :

1. 17

2. 18

3. 19

4. 21

Answer

By angle sum property of triangle,

⇒ 5(x - 4)° + (4x + 5)° + (x + 25)° = 180°

⇒ 5x° - 20° + 4x° + 5° + x° + 25° = 180°

⇒ 10x° + 10° = 180°

⇒ 10x° = 180° - 10°

⇒ 10x° = 170°

⇒ x° = $\dfrac{170°}{10}$

⇒ x° = 17°

⇒ x = 17.

Hence, option 1 is the correct option.

In △ABC, AB > AC and D is any point on BC, then, AB is :

1. < DC

2. < AD

3. = BC

4. > AD

Answer

In △ABC,

We know that,

The larger angle of a triangle has the longer side opposite to it.

⇒ AB > AC

⇒ ∠ACB > ∠ABC ....(1)

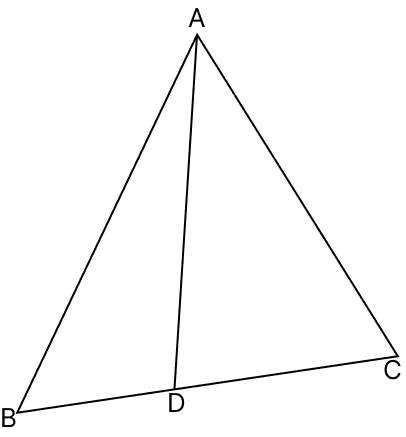
From figure,

⇒ ∠ADB > ∠ACD (exterior angle of a triangle is greater than interior opposite angle)

⇒ ∠ADB > ∠ACB ....(2)

From eq.(1) and (2), we have:

⇒ ∠ADB > ∠ABC

⇒ ∠ADB > ∠ABD

⇒ AB > AD (larger angle of a triangle has the larger side opposite to it).

Hence, option 4 is the correct option.

Case Study

Ms Anu Gupta teaches mathematics to class 9 in a school. One day she drew a figure on the board in the class. She provided the following clues to the students.

AB || CD

O is the mid-points of AD

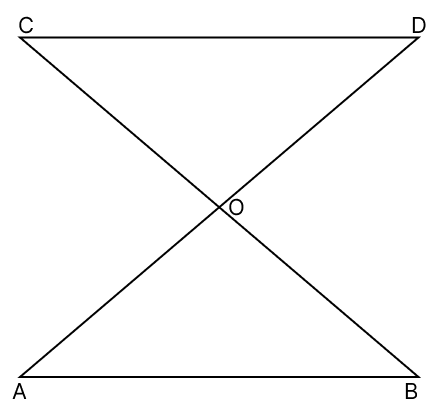
Based on this information, answer the following questions:

1. △OAB ≅ △ODC by which of the following congruent condition?
   (a) SAS
   (b) ASA
   (c) SSS
   (d) RHS

2. ∠AOB = ∠DOC holds because:
   (a) Alternate angles are equal
   (b) Corresponding angles are equal
   (c) Vertically opposite angles are equal
   (d) None of these

3. Which of the following is correct?
   (a) ∠A = ∠C
   (b) ∠B = ∠D
   (c) ∠B = ∠C
   (d) ∠AOB = ∠OCB

4. Which of the following is correct?
   (a) AO = OB
   (b) AB = OB
   (c) OD = CD
   (d) OC = OB

5. Which of the following is not a congruent condition?
   (a) ASA
   (b) SSS
   (c) AAA
   (d) AAS

Answer

1. Given,

AB || CD

In △OAB and △ODC,

⇒ AO = DO (∵ O is the mid-point of AD)

⇒ ∠BAO = ∠CDO (Alternate angles are equal)

⇒ ∠AOB = ∠DOC (Vertically opposite angles are equal)

∴ △OAB ≅ △ODC (By A.S.A axiom)

Hence, option (b) is the correct option.

2. ∠AOB and ∠DOC are vertically opposite angles, which are always equal.

Hence, option (c) is the correct option.

3. Since, △OAB ≅ △ODC

⇒ ∠B = ∠C (Corresponding parts of congruent triangle are equal.)

Hence, option (c) is the correct option.

4. Since, △OAB ≅ △ODC

⇒ OC = OB (Corresponding parts of congruent triangles are equal)

Hence, option (d) is the correct option.

5. Angle-Angle-Angle(AAA) ensures corresponding angles are equal but corresponding sides of a triangle may vary.

Thus, AAA is not a congruent condition.

Hence, option (c) is the correct option.

Assertion (A): The orthocentre of a triangle may lie in the exterior of the triangle.

Reason (R): The point of intersection of the medians of a triangle is called its orthocentre.

1. A is true, R is false

2. A is false, R is true

3. Both A and R are true

4. Both A and R are false

Answer

The point of intersection of the altitudes of a triangle is called orthocentre.

∴ Reason (R) is false.

In case of an obtuse angled triangle, altitudes of a triangle intersects outside of the triangle.

∴ Assertion (A) is true.

Hence, option 1 is the correct option.

Assertion (A): If three angles of a triangle are equal to the corresponding three angles of another triangle, then the triangles are congruent.

Reason (R): Two triangles are said to be congruent, if and only if, one of them can be made to superimpose on the other so as to cover exactly.

1. A is true, R is false

2. A is false, R is true

3. Both A and R are true

4. Both A and R are false

Answer

If three angles of a triangle are equal to the corresponding three angles of another triangle, then the triangles are similar not necessarily congruent.

∴ Assertion (A) is false.

Two triangles are said to be congruent, if both corresponding sides and angles to be equal i.e. once of triangle can be made to superimpose on other.

∴ Reason (R) is true.

Hence, option 2 is the correct option.

Assertion (A): In △ABC, D is a point on side BC. AB + BC + AC > 2AD

Reason (R): Sum of two sides of a triangle is greater than the third side.

1. A is true, R is false

2. A is false, R is true

3. Both A and R are true

4. Both A and R are false

Answer

We know that,

Sum of two sides of a triangle is greater than the third side is fundamental property of triangle.

∴ Reason (R) is true.

In △ABD,

⇒ AB + BD > AD ...(1) [Sum of any two sides of triangle is greater than the third side]

In △ADC,

⇒ AC + CD > AD ...(2) [Sum of any two sides of triangle is greater than the third side]

Adding eq.(1) and (2), we have:

⇒ AB + BD + AC + CD > AD + AD

⇒ AB + AC + BD + CD > 2AD

⇒ AB + AC + BC > 2AD

∴ Assertion (A) is true.

Hence, option 3 is the correct option.

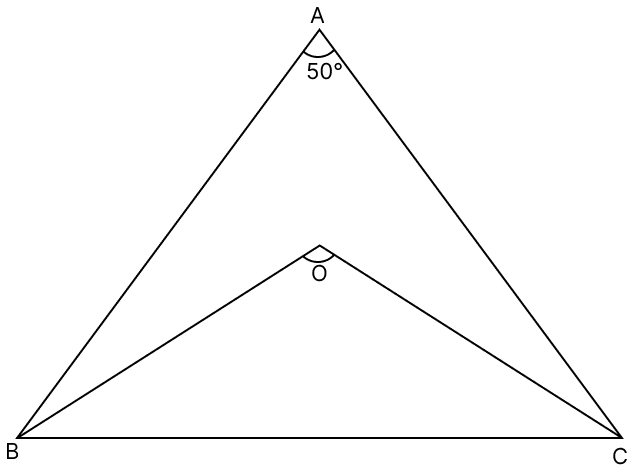
In the given figure, the bisectors of ∠B and ∠C intersect each other at O and ∠BAC = 50°. The measure of ∠BOC is :

1. 100°

2. 115°

3. 130°

4. 140°

Answer

In △ABC,

By angle sum property of triangle,

∠A + ∠B + ∠C = 180°

⇒ 50° + ∠B + ∠C = 180°

⇒ ∠B + ∠C = 180° - 50°

⇒ ∠B + ∠C = 130° .......(1)

From figure,

As, OB is bisector of angle B.

∠B = ∠ABO + ∠OBC = ∠OBC + ∠OBC = 2∠OBC

⇒ ∠OBC = $\dfrac{∠B}{2}$

As, OC is bisector of angle C.

∠C = ∠ACO + ∠OCB = ∠OCB + ∠OCB = 2∠OCB

⇒ ∠OCB = $\dfrac{∠C}{2}$

In △OBC,

By angle sum property of triangle,

⇒ ∠OBC + ∠BOC + ∠OCB = 180°

⇒ $\dfrac{∠B}{2}$ + ∠BOC + $\dfrac{∠C}{2}$ = 180°

⇒ ∠BOC + $\dfrac{∠B + ∠C}{2}$ = 180°

⇒ ∠BOC + $\dfrac{130°}{2}$ = 180° [Substituting from eq.(1)]

⇒ ∠BOC + 65° = 180°

⇒ ∠BOC = 180° - 65°

⇒ ∠BOC = 115°.

Hence, option 2 is the correct option.

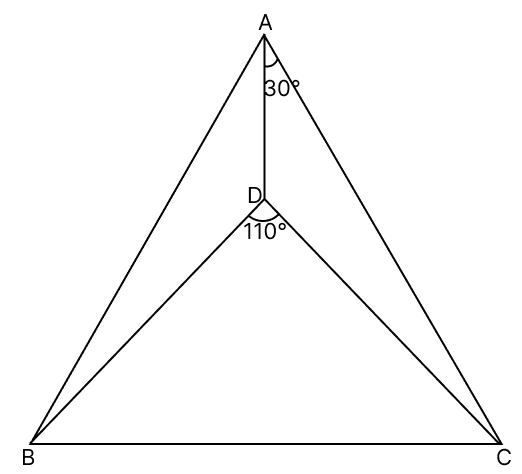
In the given figure, △ABD ≅ △ACD. If ∠DAC = 30° and ∠BDC = 110°, then the measure of ∠DBA is :

1. 30°

2. 50°

3. 70°

4. 25°

Answer

Given,

△ABD ≅ △ACD

Since, corresponding parts of congruent triangles are equal.

⇒ ∠DBA = ∠ACD = y (let)

⇒ ∠ADB = ∠ADC = x (let)

From figure,

⇒ ∠ADB + ∠ADC + ∠BDC = 360°

⇒ x + x + 110° = 360°

⇒ 2x = 360° - 110°

⇒ 2x = 250°

⇒ x = $\dfrac{250°}{2}$

⇒ x = 125°

⇒ ∠ADC = 125°

In △ADC,

By angle sum property of triangle,

⇒ ∠ADC + ∠ACD + ∠CAD = 180°

⇒ 125° + y + 30° = 180°

⇒ 155° + y = 180°

⇒ y = 180° - 155°

⇒ y = 25°

⇒ ∠DBA = y = 25°.

Hence, option 4 is the correct option.

ABC is a triangle in which AC = BC and ∠BAC = 50°. Side BC is produced to D such that BC = CD. ∠BAD is equal to :

1. 45°

2. 50°

3. 90°

4. 100°

Answer

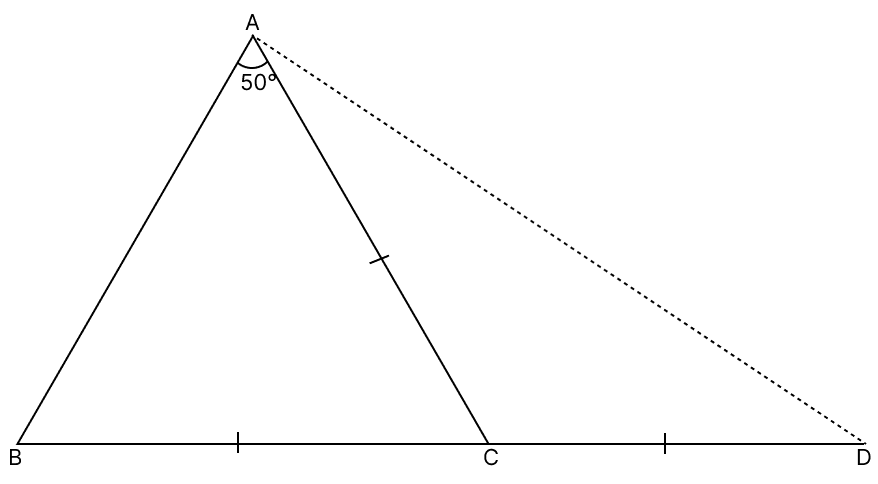
Given,

AC = BC

∠BAC = ∠ABC = 50°

In △ABC,

By angle sum property of triangle,

∠BAC + ∠ABC + ∠ACB = 180°

⇒ 50° + 50° + ∠ACB = 180°

⇒ 100° + ∠ACB = 180°

⇒ ∠ACB = 180° - 100°

⇒ ∠ACB = 80°

From figure,

∠ACD + ∠ACB = 180° (Linear pair)

⇒ ∠ACD + 80° = 180°

⇒ ∠ACD = 180° - 80°

⇒ ∠ACD = 100°

In △ACD,

AC = CD

∠CAD = ∠ADC = x (let)

By angle sum property of triangle,

⇒ ∠ADC + ∠CAD + ∠ACD = 180°

⇒ x + x + 100° = 180°

⇒ 2x = 180° - 100°

⇒ 2x = 80°

⇒ x = $\dfrac{80°}{2}$

⇒ x = 40°.

⇒ ∠CAD = ∠ADC = 40°.

From figure,

∠BAD = ∠BAC + ∠CAD = 50° + 40° = 90°.

Hence, option 3 is the correct option.

ABD is a triangle such that ∠ADB = 20° and C is a point on BD such that AB = AC and CD = CA. The measure of ∠ABC :

1. 40°

2. 50°

3. 55°

4. 60°

Answer

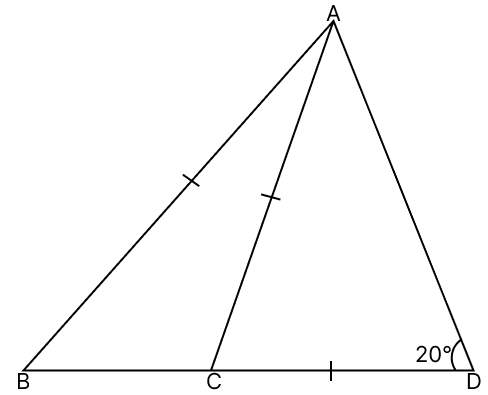
In △ADC,

CD = CA

∠ADC = ∠CAD = 20° (Angles opposite to equal sides in a triangle are equal)

In △ACD,

By angle sum property of triangle,

⇒ ∠ACD + ∠ADC + ∠CAD = 180°

⇒ ∠ACD + 20° + 20° = 180°

⇒ ∠ACD + 40° = 180°

⇒ ∠ACD = 180° - 40°

⇒ ∠ACD = 140°

From figure,

∠ACB + ∠ACD = 180° (Linear pair)

⇒ ∠ACB + 140° = 180°

⇒ ∠ACB = 180° - 140°

⇒ ∠ACB = 40°

In △ABC,

AB = AC

∠ABC = ∠ACB = 40° (Angles opposite to equal sides in a triangle are equal)

Hence, option 1 is the correct option.

The lengths of the three sides of a triangle are 4 cm, 5 cm, and 7 cm. Which of the following cannot be the length of any one of the medians?

1. 2.5 cm

2. 3.8 cm

3. 5 cm

4. None of these

Answer

Suppose there is a triangle with sides of length a, b and c, then the median to side a is always less than the sum of other two sides.

Thus, in this case each of the following options can be the length of the median of triangle.

Hence, option 4 is the correct option.

In △ABC, ∠B = 35°, ∠C = 65° and the bisector AD of ∠BAC meets BC at D. Arrange the sides AD, BD and CD in ascending order of their lengths.

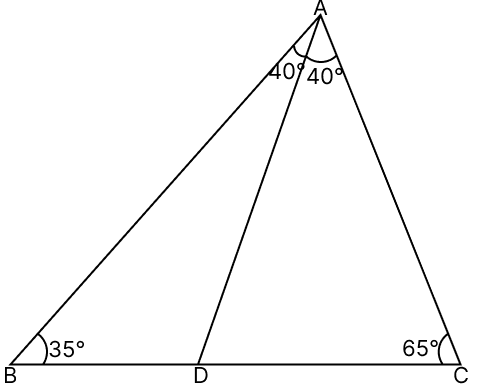
Answer

In △ADB,

⇒ ∠BAD + ∠ADB + ∠ABD = 180°

⇒ 40° + ∠ADB + 35° = 180°

⇒ ∠ADB + 75° = 180°

⇒ ∠ADB = 180° - 75°

⇒ ∠ADB = 105°.

We know that,

The shortest side of a triangle has the smallest angle opposite to it.

In triangle ABD,

Since,

⇒ ∠B < ∠A

⇒ AD < BD .......(1)

From figure,

∠ADB + ∠ADC = 180° (Linear pair)

⇒ ∠ADC + 105° = 180°

⇒ ∠ADC = 180° - 105°

⇒ ∠ADC = 75°

In triangle ACD,

Since,

⇒ ∠A < ∠C

⇒ CD < AD ........(2)

From eq.(1) and (2) we have:

⇒ CD < AD < BD

Hence, CD < AD < BD.

In the given figure, find the value of a + b + c + d + e + f.

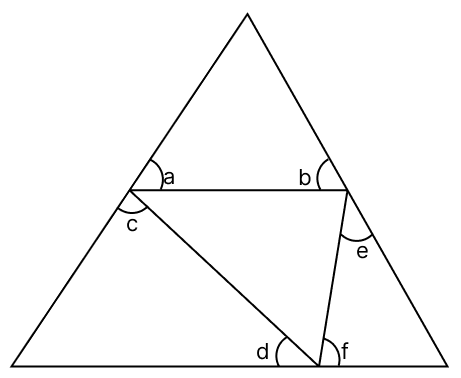
Answer

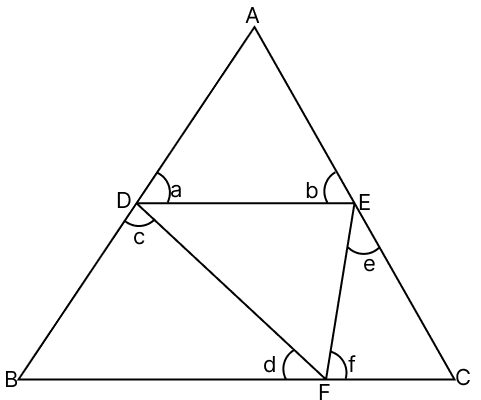
In △AED,

⇒ a + b + ∠A = 180° ....(1)

In △DBF,

⇒ c + d + ∠B = 180° ....(2)

In △EFC,

⇒ e + f + ∠C = 180° ....(3)

In △ABC,

⇒ ∠A + ∠B + ∠C = 180° ....(4)

Adding eq.(1), (2) and (3), we get :

⇒ a + b + c + d + e + f + ∠A + ∠B + ∠C = 180° + 180° + 180°

⇒ a + b + c + d + e + f + 180° = 540°

⇒ a + b + c + d + e + f = 540° - 180°

⇒ a + b + c + d + e + f = 360°.

Hence, the value of a + b + c + d + e + f = 360°.