Mid-Point Theorem and Intercept Theorem

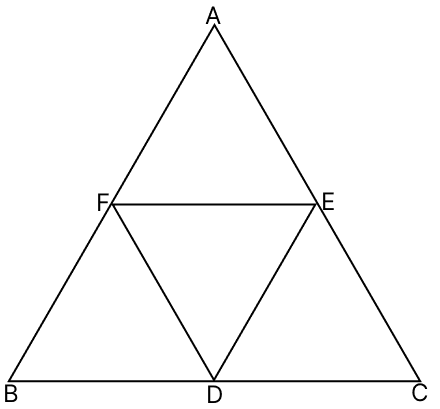
In the given figure, D, E, F are the mid-points of the sides BC, CA and AB respectively.

(i) If AB = 6.2 cm, find DE

(ii) If DF = 3.8 cm, find AC

(iii) If perimeter of △ABC is 21 cm, find FE

Answer

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and equal to half of it.

(i) Since, E and D are the mid-points of AC and BC respectively.

By mid-point theorem,

⇒ DE = $\dfrac{1}{2}AB = \dfrac{1}{2}$ × 6.2 = 3.1 cm

Hence, DE = 3.1 cm.

(i) Since, F and D are the mid-points of AB and BC respectively.

⇒ DF = $\dfrac{1}{2}$ AC

⇒ AC = 2 × 3.8

⇒ AC = 7.6 cm

Hence, AC = 7.6 cm.

(iii) From above,

AC = 7.6 cm, AB = 6.2 cm

Given,

Perimeter of △ABC = 21 cm

⇒ AB + AC + BC = 21

⇒ 6.2 + 7.6 + BC = 21

⇒ BC + 13.8 = 21

⇒ BC = 21 - 13.8

⇒ BC = 7.2 cm

Since, F and E are the mid-points of AB and AC respectively.

⇒ FE = $\dfrac{1}{2}$ BC

⇒ FE = $\dfrac{1}{2}$ × 7.2

⇒ FE = 3.6 cm

Hence, FE = 3.6 cm.

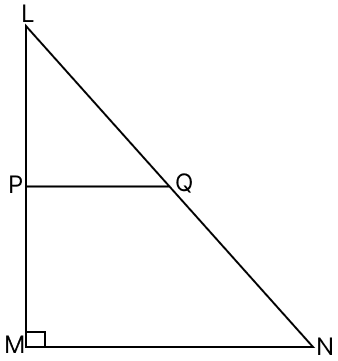
In the given figure, LMN is a right triangle in which ∠M = 90°, P and Q are mid-points of LM and LN respectively. If LM = 9 cm, MN = 12 cm and LN = 15 cm, find :

(i) the perimeter of trapezium MNQP

(ii) the area of trapezium MNQP

Answer

Since, P is mid-point of LM,

LP = PM

From figure,

⇒ LM = LP + PM

⇒ 9 = PM + PM

⇒ 9 = 2 PM

⇒ PM = $\dfrac{9}{2}$

⇒ PM = 4.5 cm

Since, Q is mid-point of LN,

LQ = QN

From figure,

⇒ LN = LQ + QN

⇒ 15 = QN + QN

⇒ 15 = 2 QN

⇒ QN = $\dfrac{15}{2}$

⇒ QN = 7.5 cm

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and equal to half of it.

Since, P and Q are the mid-points of LM and LN respectively.

⇒ PQ = $\dfrac{1}{2}MN = \dfrac{1}{2}$ × 12 = 6 cm

(i) Perimeter of trapezium MNQP = PM + PQ + QN + MN

⇒ 4.5 + 6 + 7.5 + 12

⇒ 30 cm.

Hence, perimeter of trapezium MNQP = 30 cm.

(ii) Area of trapezium MNQP = $\dfrac{1}{2}$ × (Sum of parallel sides) × height of trapezium

= $\dfrac{1}{2}$ × (PQ + MN) × PM

= $\dfrac{1}{2}$ × (6 + 12) × 4.5

= $\dfrac{1}{2}$ × 18 × 4.5

= 40.5 cm²

Hence, area of trapezium MNQP is 40.5 cm².

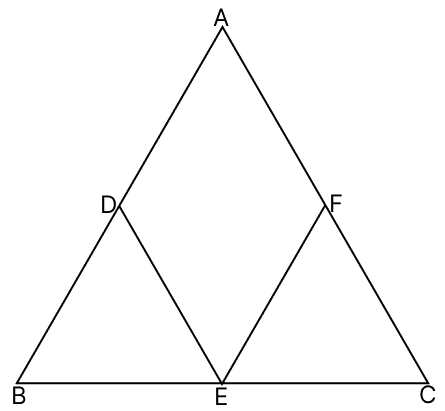
In the given figure, D, E, F are respectively the mid-points of the sides AB, BC and CA of △ABC. Prove that ADEF is a parallelogram.

Answer

Given,

D, E, F are respectively the mid-points of the sides AB, BC and CA of △ABC. Thus,

AD = DB, AF = FC and BE = EC

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and equal to half of it.

Since, D and E are the mid-points of AB and BC respectively.

⇒ DE || AC

⇒ DE || AF .....(1)

Since, F and E are the mid-points of AC and BC respectively.

⇒ FE || AB

⇒ FE || AD .....(2)

In quadrilateral ADEF,

AD // FE and DE // AF

Since, opposite sides of quadrilateral ADEF are parallel.

∴ ADEF is a parallelogram.

Hence, proved that ADEF is a parallelogram.

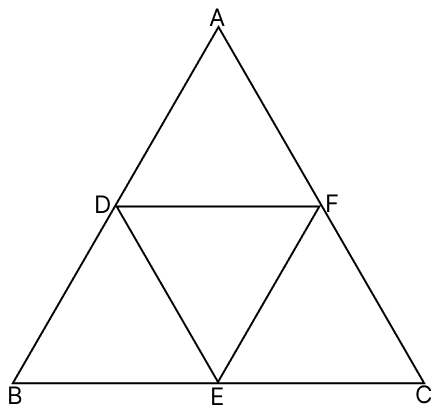
If D, E, F are respectively the mid-points of the sides AB, BC and CA of an equilateral triangle ABC, prove that △DEF is also an equilateral triangle.

Answer

Given,

△ABC is an equilateral triangle.

⇒ AB = BC = AC

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and equal to half of it.

Since, D and E are the mid-points of AB and BC respectively.

⇒ DE = $\dfrac{1}{2}$ × AC

⇒ DE = $\dfrac{1}{2}$ × AB [As AB = AC = BC] ....(1)

Since, D and F are the mid-points of AB and AC respectively.

⇒ DF = $\dfrac{1}{2}$ × BC

⇒ DF = $\dfrac{1}{2}$ × AB [As AB = AC = BC] ....(2)

Since, E and F are the mid-points of BC and AC respectively.

⇒ EF = $\dfrac{1}{2}$ × AB ....(3)

From eq.(1), (2) and (3), we have:

⇒ DE = DF = EF

∴ △DEF is an equilateral triangle.

Hence, proved that △DEF is an equilateral triangle.

In the adjoining figure, ABCD is a quadrilateral in which AD = BC and P, Q, R, S are the mid-points of AB, BD, CD and AC respectively. Prove that PQRS is a rhombus.

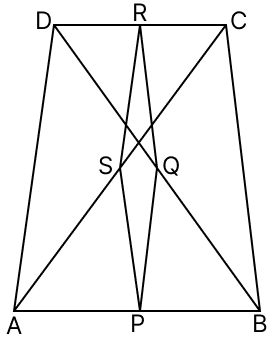
Answer

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and equal to half of it.

In △ABD,

Since, P and Q are the mid-points of AB and BD respectively.

PQ || AD

⇒ PQ = $\dfrac{1}{2}$ × AD .....(1)

In △BCD,

Since, R and Q are the mid-points of DC and BD respectively.

QR || BC

⇒ QR = $\dfrac{1}{2}$ × BC

⇒ QR = $\dfrac{1}{2}$ × AD (∵ AD = BC) .....(2)

In △ABC,

Since, P and S are the mid-points of AB and AC respectively.

PS || BC

⇒ PS = $\dfrac{1}{2}$ × BC

⇒ PS = $\dfrac{1}{2}$ × AD (∵ AD = BC) .....(3)

In △ADC,

Since, S and R are the mid-points of AC and DC respectively.

SR || AD

⇒ SR = $\dfrac{1}{2}$ × AD .....(4)

From eq.(1), (2), (3) and (4), we have:

⇒ PQ = SR = QR = PS

Since, PQ || SR (Both are parallel to AD) and QR || PS (both are parallel to BC)

∴ PQRS is rhombus.

Hence, proved that PQRS is a rhombus.

In the adjoining figure, ABCD is a parallelogram in which E is the mid-point of DC and F is a point on AC such that CF = $\dfrac{1}{4}$ AC. If EF is produced to meet BC in G, prove that G is the mid-point of BC.

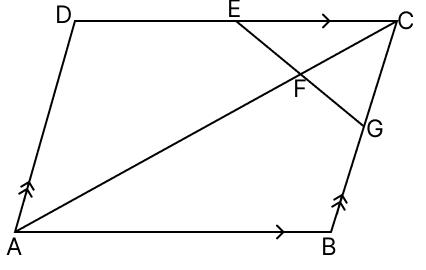
Answer

Join BD. Let BD intersect AC at point O.

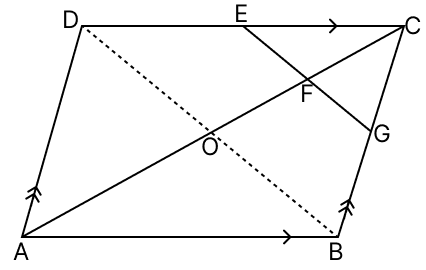
We know that,

The diagonals of a parallelogram bisect each other.

AO = CO and OD = OB

Given,

⇒ CF = $\dfrac{1}{4}$ AC

⇒ CF = $\dfrac{1}{4}$ (AO + CO)

⇒ CF = $\dfrac{1}{4}$ (CO + CO)

⇒ CF = $\dfrac{1}{4}$ 2 CO

⇒ CF = $\dfrac{1}{2}$ CO

∴ F is the mid-point of CO.

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and equal to half of it.

In △COD,

Since, E and F are the mid-points of DC and OC respectively.

EF || OD

Since, EG and BD are straight lines. Thus, FG || OB

By converse of mid-point theorem,

The straight line drawn through the mid-point of one side of a triangle parallel to another, bisects the third side.

In △COB,

Since, F is the mid-point of CO and FG || OB

∴ G is the mid-point of BC.

Hence, proved that G is the mid-point of BC.

In the adjoining figure, ABCD is a kite in which AB = AD and CB = CD. If E, F, G are respectively the mid-points of AB, AD and CD, prove that :

(i) ∠EFG = 90°

(ii) If GH || FE, then H bisects CB.

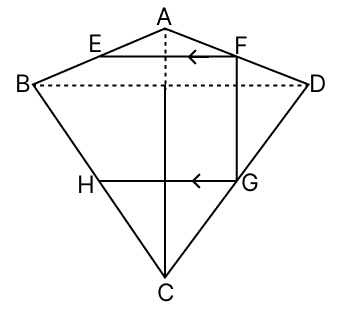
Answer

Join AC and BD, AC and BD intersects at O.

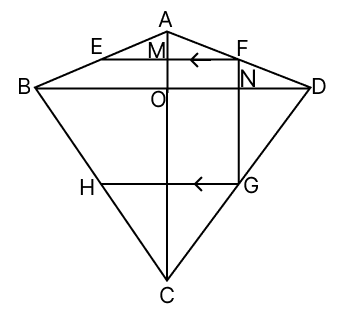
(i) We know that,

Diagonals of a kite intersect at right angles.

∠MON = 90° ...(1)

By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

In △ABD,

E and F are mid-points of AB and AD,

EF || BD and EF = $\dfrac{1}{2}$ BD

By converse of mid-point theorem,

The straight line drawn through the mid-point of one side side of a triangle parallel to another, bisects the third side.

In △ABO,

E is the mid-point of AB and EF || BD so, EM || BO,

∴ M is the mid-point of AO

⇒ AM = MO

In △AOD,

M and F are mid-points of AO and AD,

MF || OD and MF = $\dfrac{1}{2}$ OD ...(1)

In △ADC,

G and F are mid-points of CD and AD,

FG || AC and FG = $\dfrac{1}{2}$ AC (By mid-point theorem)

In △AOD,

F is the mid-point of AD and FG || AC so, FN || AO,

∴ N is the mid-point of OD (By converse of mid-point theorem)

⇒ ON = ND

From eq.(1), we have:

MF || OD and MF = $\dfrac{1}{2}$ OD

⇒ MF = ON

∴ OMFN is a parallelogram.

We know that,

Opposite angles of a parallelogram are equal.

⇒ ∠MON = ∠MFN = 90°

From figure,

∠EFG = ∠MFN = 90°

Hence, proved that ∠EFG = 90°.

(ii) EF || BD (Proved above)

A line through G is parallel to EF.

∴ GH || FE

or GH || BD

In △BCD,

GH || BD and G is mid-point of CD.

By converse of mid-point theorem,

The straight line drawn through the mid-point of one side side of a triangle parallel to another, bisects the third side.

∴ H is the mid-point of BC (By converse of mid-point theorem)

Hence, proved that if GH || FE, then H bisects CB.

In the adjoining figure, ABCD is a parallelogram, E is the mid-point of CD and through D, a line is drawn parallel to EB to meet CB produced at G and intersecting AB at F. Prove that :

(i) AD = $\dfrac{1}{2}$ GC

(ii) DG = 2 EB

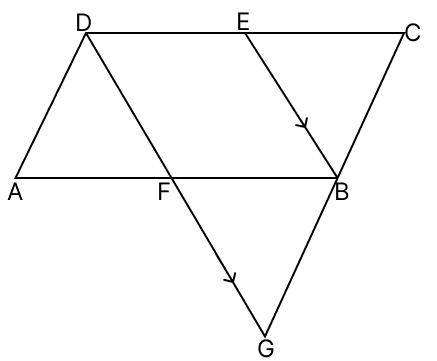
Answer

By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

By converse of mid-point theorem,

The straight line drawn through the mid-point of one side side of a triangle parallel to another, bisects the third side.

Given, DF || EB

⇒ DG || EB

In △ DGC,

⇒ E is the mid-point of CD and DG || EB.

∴ B is the mid-point of GC. (By converse of mid-point theorem)

∴ BG = BC

Thus, BC = $\dfrac{1}{2}GC$

(i) We know that,

Opposite sides of a parallelogram are equal.

⇒ AD = BC

⇒ AD = $\dfrac{1}{2}$ GC

Hence, proved that AD = $\dfrac{1}{2}$ GC.

(ii) In △DGC,

Since, E and B are the mid-points of DC and GC respectively.

EB || DG

Thus, by mid-point theorem,

⇒ EB = $\dfrac{1}{2}$ DG

⇒ DG = 2 EB.

Hence, proved that DG = 2EB.

In the adjoining figure, in △ABC, AD is the median through A and E is the mid-point of AD. If BE produced meets AC in F, prove that AF = $\dfrac{1}{3}$ AC.

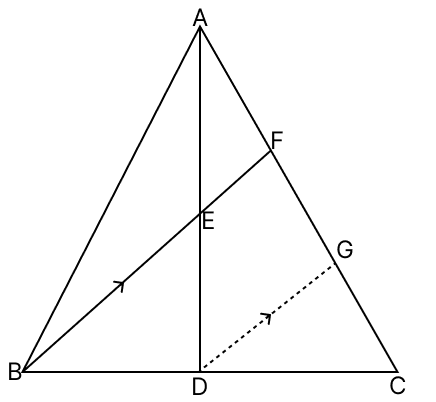
Answer

By converse of mid-point theorem,

A line drawn through the midpoint of one side of a triangle, and parallel to another side, will bisect the third side.

Given,

AD is the median to BC.

BD = CD

In △BCF,

Since, D is the mid-point of BC and DG // BF, thus by converse of mid-point theorem,

DG will bisect CF, thus G is the mid-point of CF.

⇒ CG = GF ......(1)

In △ADG,

Since, E is the mid-point of AD and EF // DG, thus by converse of mid-point theorem,

EF will bisect AG, thus F is the mid-point of AG.

⇒ AF = GF ........(2)

From (1) and (2),

⇒ AF = GF = CG

From figure,

⇒ AC = AF + GF + CG

⇒ AC = AF + AF + AF

⇒ AC = 3 AF

⇒ AF = $\dfrac{1}{3}$ AC.

Hence, proved that AF = $\dfrac{1}{3}$ AC.

In the adjoining figure, △ABC is right-angled at B and P is the mid-point of AC. Show that, PA = PB = PC.

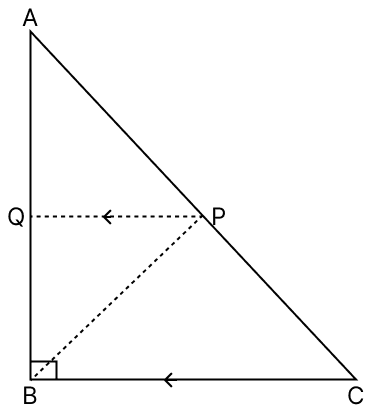
Answer

Given,

P is mid-point of AC,

∴ PA = PC .........(1)

From figure,

PQ // CB

∠AQP = ∠ABC = 90° (Corresponding angles are equal)

⇒ ∠AQP + ∠PQB = 180° (Linear pair)

⇒ 90° + ∠PQB = 180°

⇒ ∠PQB = 180° - 90°

⇒ ∠PQB = 90°

By converse of mid-point theorem,

A line drawn through the midpoint of one side of a triangle, and parallel to another side, will bisect the third side.

In △ABC,

Since, P is the mid-point of AC and PQ // CB, thus by converse of mid-point theorem,

PQ will bisect AB, thus Q is the mid-point of AB.

In △AQP and △BQP,

⇒ ∠AQP = ∠PQB (Each equal to 90°)

⇒ PQ = PQ (Common side)

⇒ AQ = BQ (Q is the mid-point of AB)

Thus, △AQP ≅ △BQP. (By S.A.S. axiom)

∴ PB = PA (Corresponding parts of congruent triangles are equal) .........(2)

From (1) and (2), we get :

⇒ PB = PA = PC

Hence, proved that PA = PB = PC.

Show that the quadrilateral formed by joining the mid-points of the pairs of adjacent sides of a rectangle is a rhombus.

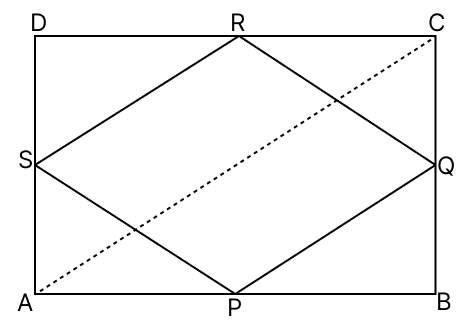
Answer

Join BD.

By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

In △ABC,

Since, P and Q are the mid-points of AB and BC respectively.

By mid-point theorem,

⇒ PQ || AC and PQ = $\dfrac{1}{2}$ AC ...(1)

In △ADC,

Since, S and R are the mid-points of AD and CD respectively.

⇒ SR || AC and SR = $\dfrac{1}{2}$ AC ...(2)

From eq.(1) and (2), we have :

PQ = SR and PQ || SR ...(3)

In △ABD,

Since, P and S are the mid-points of AB and AD respectively.

PS || BD

⇒ PS = $\dfrac{1}{2}$ BD ...(4)

In △BCD,

Since, Q and R are the mid-points of BC and CD respectively.

QR || BD

⇒ QR = $\dfrac{1}{2}$ BD ...(5)

From eq.(4) and (5), we have:

PS = QR and PS || QR ...(6)

From eq.(3) and (6), we have:

In quadrilateral PQRS opposite sides are parallel and equal.

∴ PQRS is a parallelogram.

Given,

ABCD is a rectangle.

AB = CD and AD = BC

In △ASP and △BQP,

⇒ AP = BP (P is the mid-point of AB)

⇒ AS = BQ (As, S and Q are mid-points of equal sides AD and BC respectively)

⇒ ∠SAP = ∠QBP (Both equal to 90°)

∴ △ASP ≅ △BQP (By S.A.S axiom)

⇒ PS = PQ ....(7) (Corresponding parts of congruent traingles are equal)

From eq.(3), (6) and (7), we have:

PS = PQ = QR = SR

Since, all sides are equal and opposite sides are parallel,

∴ PQRS is a rhombus.

Hence, the quadrilateral formed by joining the mid-points of the pairs of adjacent sides of a rectangle is a rhombus.

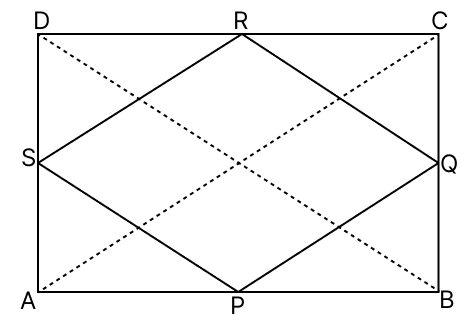
Show that the quadrilateral formed by joining the mid-points of the pairs of adjacent sides of a rhombus is a rectangle.

Answer

By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

In △ABC,

Since, P and Q are the mid-points of AB and BC respectively.

PQ || AC

⇒ PQ = $\dfrac{1}{2}$ AC ...(1)

In △ADC,

Since, S and R are the mid-points of AD and CD respectively.

SR || AC

⇒ SR = $\dfrac{1}{2}$ AC ...(2)

From eq.(1) and (2), we have:

PQ = SR ...(3)

In △ABD,

Since, P and S are the mid-points of AB and AD respectively.

PS || BD

⇒ PS = $\dfrac{1}{2}$ BD ...(4)

In △BCD,

Since, Q and R are the mid-points of BC and CD respectively.

QR || BD

⇒ QR = $\dfrac{1}{2}$ BD ...(5)

From eq.(4) and (5), we have:

PS = QR ...(6)

From eq.(3) and (6), we have:

∴ PQRS is a parallelogram.

We know that,

Diagonals of rhombus intersect at right angles.

⇒ ∠EOF = 90°

In quadrilateral OERF,

ER || OF and EO || RF

∴ OERF is a parallelogram.

Opposite angles of a parallelogram are equal.

⇒ ∠EOF = ∠ERF = 90°

In parallelogram PQRS,

⇒ ∠QRS = ∠QPS = 90°

⇒ ∠PSR = ∠PQR = x (let)

∠QRS + ∠QPS + ∠PSR + ∠PQR = 360°

⇒ 90° + 90° + x + x = 360°

⇒ 180° + 2x = 360°

⇒ 2x = 360° - 180°

⇒ 2x = 180°

⇒ x = $\dfrac{180°}{2}$

⇒ x = 90°

⇒ ∠PSR = ∠PQR = 90°

Since, in parallelogram PQRS, opposite sides are equal and parallel and all the interior angles equal to 90°.

∴ PQRS is a rectangle.

Hence, proved that the quadrilateral formed by joining the mid-points of the pairs of adjacent sides of a rhombus is a rectangle.

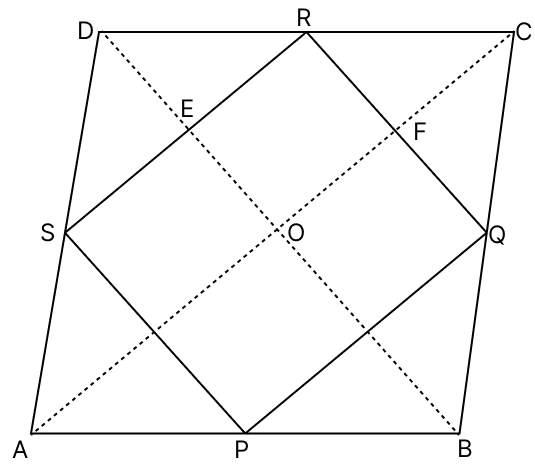
Show that the quadrilateral formed by joining the mid-points of the pairs of adjacent sides of a square is a square.

Answer

By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

Let ABCD be a square in which E, F, G and H are mid-points of AB, BC, CD and DA respectively.

We know that diagonals of a square are equal and bisect each other.

AC = BD

AO = OC = BO = OD

Join EF, FG, GH and HE.

Join AC and BD.

In △ACD,

G and H are mid-points of CD and AD respectively.

By mid-point theorem,

∴ GH || AC and GH = $\dfrac{1}{2}$ AC

GH = AO (∵ O is the mid-point of AC) ...(1)

In △ABC,

E and F are mid-points of AB and BC respectively.

∴ EF || AC and EF = $\dfrac{1}{2}$ AC

EF = AO (∵ O is the mid-point of AC) ...(2)

In △ABD,

E and H are mid-points of AB and AD respectively.

∴ EH || BD and EH = $\dfrac{1}{2}$ BD

EH = BO (∵ O is the mid-point of BD)

∴ EH = AO ...(3)

In △BCD,

G and F are mid-points of CD and BC respectively.

∴ FG || BD and FG = $\dfrac{1}{2}$ BD

FG = BO (∵ O is the mid-point of BD)

∴ FG = AO ....(4)

From eq.(1), (2), (3) and (4), we get:

EH || FG, EF || GH and EH = FG = GH = EF

Since, both the opposite sides of a quadrilateral are parallel.

∴ EFGH is a parallelogram.

In △GOH and △GOF,

⇒ OH = OF (Diagonals of parallelogram bisect each other)

⇒ OG = OG (Common side)

⇒ GH = GF (Proved above)

∴ △GOH ≅ △GOF (S.S.S axiom)

⇒ ∠GOH = ∠GOF (Corresponding parts of congruent triangles are equal)

From figure,

⇒ ∠GOH + ∠GOF = 180°

⇒ ∠GOH + ∠GOH = 180°

⇒ 2∠GOH = 180°

⇒ ∠GOH = $\dfrac{180°}{2}$

⇒ ∠GOH = 90°

So, the diagonals of EFGH bisect and are perpendicular to each other and all sides of quadrilateral EFGH are equal.

∴ EFGH is a square.

Hence, the quadrilateral formed by joining the mid-points of the pairs of adjacent sides of a square is a square.

In the adjoining figure, ABCD is a trapezium in which AB || DC. If M and N are the mid-points of AC and BD respectively. Prove that MN = $\dfrac{1}{2}$ (AB - CD).

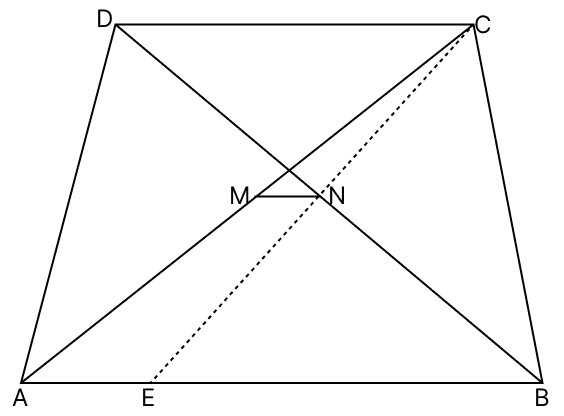
Answer

From figure,

AB // DC

EB // DC

In △BNE and △CND,

⇒ ∠BNE = ∠CND (Vertically opposite angles are equal)

⇒ ∠BEN = ∠NCD (Alternate angles are equal)

⇒ BN = DN (N is the mid-point of BD)

∴ △BNE ≅ △CND

⇒ BE = CD (Corresponding parts of congruent triangles are equal)

⇒ NE = CN (Corresponding parts of congruent triangles are equal)

∴ N is the mid-point of CE.

By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

Since, M and N are the mid-points of AC and CE respectively.

MN || AE

⇒ MN = $\dfrac{1}{2}$ AE

⇒ MN = $\dfrac{1}{2}$ (AB - BE)

⇒ MN = $\dfrac{1}{2}$ (AB - CD) (∵ BE = CD)

Hence, proved that MN = $\dfrac{1}{2}$ (AB - CD).

In the adjoining figure, ABCD is a trapezium in which AB || DC and E is the mid-point of AD. If EF || AB meets BC at F, show that F is the mid-point of BC.

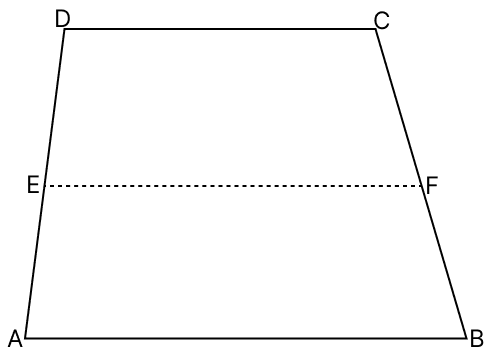
Answer

Join AC. Let AC intersects EF at O.

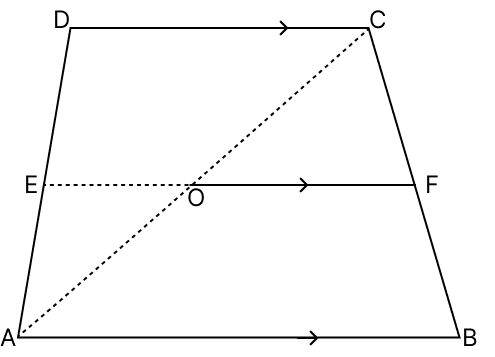
Given,

AB || DC and EF || AB

∴ EF || AB || DC

By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

By converse of mid-point theorem,

A line drawn through the midpoint of one side of a triangle, and parallel to another side, will bisect the third side.

Since,

⇒ EF || DC

⇒ EO || DC

In △ADC,

E is the mid-point of AD and EO || DC.

∴ O is the mid-point of AC. (By converse of mid-point theorem)

Given,

⇒ EF || AB

⇒ OF || AB

In △ABC,

O is the mid-point of AC and OF || AB.

∴ F is the mid-point of BC. (By converse of mid-point theorem)

Hence, proved that F is the mid-point of BC.

Two points A and B lie on the same side of a line XY. If AD ⊥ XY and BE ⊥ XY meet XY in D and E respectively and C is the mid-point of AB, show that CD = CE.

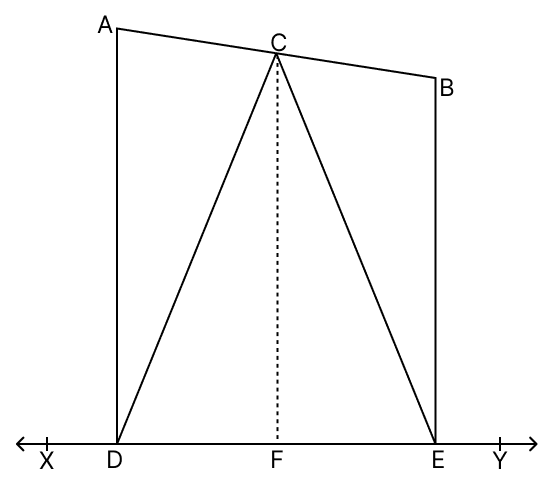
Answer

Join BD which intersects CF at O.

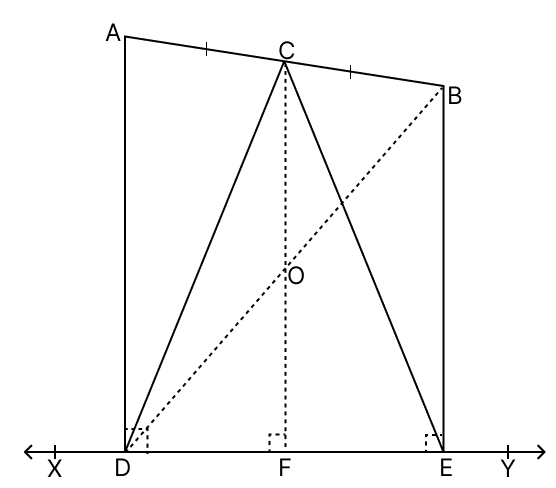
Given,

CF ⊥ XY, AD ⊥ XY and BE ⊥ XY

⇒ CF || AD || BE

By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

By converse of mid-point theorem,

A line drawn through the midpoint of one side of a triangle, and parallel to another side, will bisect the third side.

Since,

⇒ CF || AD

⇒ CO || AD

In △ADB,

C is the mid-point of AB and CO || AD.

∴ O is the mid-point of BD. (By converse of mid-point theorem)

Given,

⇒ CF || BE

⇒ OF || BE

In △BDE,

O is the mid-point of BD and OF || BE.

∴ F is the mid-point of DE. (By converse of mid-point theorem)

⇒ DF = FE

In △CDF and △CEF,

⇒ DF = FE (Proved above)

⇒ CF = CF (Common side)

⇒ ∠CFD = ∠CFE (Both equal to 90°)

∴ △CDF ≅ △CEF (By S.A.S. axiom)

⇒ CD = CE (Corresponding parts of congruent triangles are equal)

Hence, proved that CD = CE.

Prove that the straight lines joining the mid-points of the opposite sides of a quadrilateral bisect each other.

Answer

Let ABCD be the quadrilateral and E, F, G and H be the mid-point of AD, AB, BC and CD.

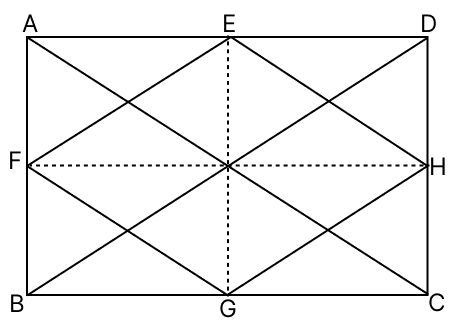
By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

Let ABCD be the quadrilateral and E, F, G and H are the mid-points of sides AD, AB, BC and CD.

In △BCD,

Since, G and H are the mid-points of BC and CD respectively.

⇒ GH || BD and GH = $\dfrac{1}{2}$ BD ...(1)

In △BAD,

Since, F and E are the mid-points of AB and AD respectively.

⇒ FE || BD and FE = $\dfrac{1}{2}$ BD ...(2)

From eq.(1) and (2), we have :

⇒ GH = FE and FE || GH

∴ EFGH is a parallelogram.

We know that,

Diagonals of the parallelogram, bisect each other.

EG and FH are the diagonals of parallelogram EFGH bisects each other.

Hence, proved that the straight lines joining the mid-points of the opposite sides of a quadrilateral bisect each other.

BP and CQ are two medians of a △ABC. If QP = 4 cm, then BC =

1. 2 cm

2. 6 cm

3. 8 cm

4. 9 cm

Answer

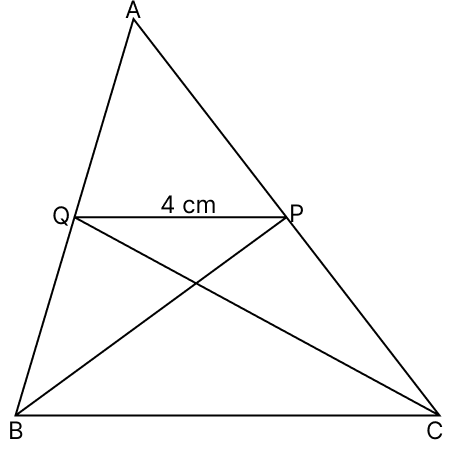
Given,

BP is the median.

∴ P is the mid-point of AC

CQ is the median.

∴ Q is the mid-point of AB

By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

Since, Q and P are the mid-points of AB and AC respectively. Thus,

⇒ QP || BC and QP = $\dfrac{1}{2}$ BC

⇒ BC = 2 × QP

⇒ BC = 2 × 4

⇒ BC = 8 cm.

Hence, option 3 is the correct option.

ABC is a right angled isosceles triangle in which ∠A = 90°. If D and E are the mid-points of AB and AC respectively, then ∠ADE =

1. 30°

2. 45°

3. 60°

4. 90°

Answer

Given,

ABC is a right angled isosceles triangle. Since, hypotenuse is the largest side thus other two sides of triangle will be equal.

AC = AB

⇒ ∠C = ∠B = x (let)

In △ABC,

⇒ ∠A + ∠B + ∠C = 180°

⇒ 90° + x + x = 180°

⇒ 2x = 180° - 90°

⇒ 2x = 90°

⇒ x = $\dfrac{90°}{2}$

⇒ x = 45°

⇒ ∠C = ∠B = 45°

By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

Since, D and E are the mid-points of AB and AC respectively.

DE || BC

AB is the transversal.

⇒ ∠ABC = ∠ADE (Corresponding angles are equal)

⇒ ∠ADE = 45°.

Hence, option 2 is the correct option.

On the sides AB and AC of a △ABC, D and E are two points such that AD : AB = AE : AC = 1 : 2. If BC = 7 cm, then DE =

1. 3.5 cm

2. 7 cm

3. 14 cm

4. 15 cm

Answer

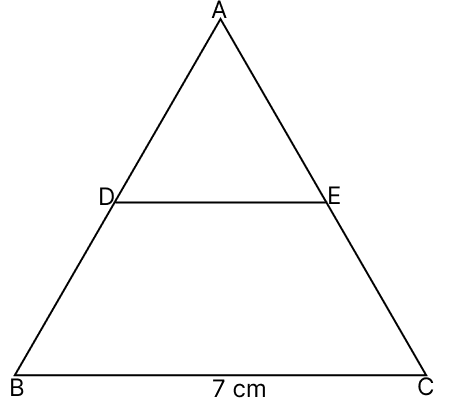
Given,

AD : AB = 1 : 2

⇒ AB = 2 AD

∴ D is the mid-point of AB

AE : AC = 1 : 2

⇒ AC = 2 AE

∴ E is the mid-point of AC

By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

Since, D and E are the mid-points of AB and AC respectively.

⇒ DE = $\dfrac{1}{2} BC = \dfrac{1}{2}$ × 7 = 3.5 cm

Hence, option 1 is the correct option.

AD and BE are two medians of a ABC. F is a point on AC such that DF || BE. If AC = 12 cm, then FC =

1. 6 cm

2. 4 cm

3. 3 cm

4. none of these

Answer

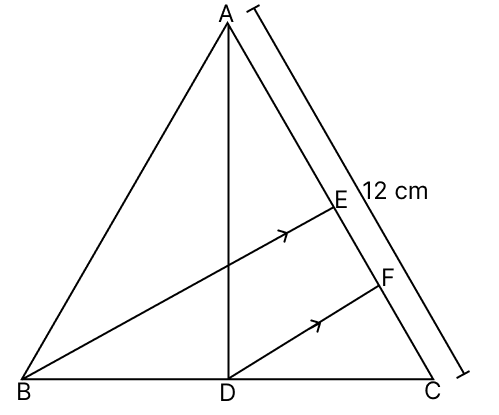
In △BCE,

D is the midpoint of BC (As AD is median)

Given,

DF || BE

By converse of mid-point theorem,

A line drawn through the midpoint of one side of a triangle, and parallel to another side, will bisect the third side.

Thus, in triangle BEC,

F is the mid-point of CE

⇒ FC = $\dfrac{1}{2}$ CE ....(1)

Given,

BE is median.

⇒ E is the mid-point of AC

⇒ AE = CE

⇒ CE = $\dfrac{1}{2}$ AC

Substituting value of CE in eq.(1), we get:

⇒ FC = $\dfrac{1}{2} \times \dfrac{1}{2} \text{AC}$

⇒ FC = $\dfrac{1}{4} \times 12$

⇒ FC = 3 cm.

Hence, option 3 is the correct option.

D, E and F are respectively the mid-points of the sides BC, CA and AB of a ABC. If BC = 10 cm, CA = 12 cm and AB = 17 cm, then the perimeter of the DEF is :

1. 13 cm

2. 19.5 cm

3. 39 cm

4. None of these

Answer

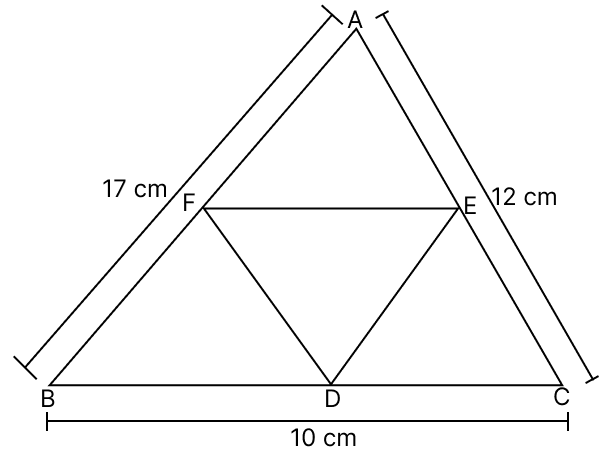
By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

Since, F and E are the mid-points of AB and AC respectively.

⇒ FE || BC and FE = $\dfrac{1}{2} BC = \dfrac{1}{2}$ × 10 = 5 cm

Since, F and D are the mid-points of AB and BC respectively.

⇒ FD || AC and FD = $\dfrac{1}{2} AC = \dfrac{1}{2}$ × 12 = 6 cm

Since, D and E are the mid-points of BC and AC respectively.

⇒ DE || AB and DE = $\dfrac{1}{2}AB = \dfrac{1}{2}$ × 17 = 8.5 cm

Perimeter of DEF = DE + FE + FD = 8.5 + 5 + 6 = 19.5 cm

Hence, option 2 is the correct option.

D, E and F are respectively the mid-points of the sides BC, CA and AB of a ABC. If BC = 12 cm, CA = 15 cm and AB = 18 cm, then the perimeter of the quadrilateral DEAF is :

1. 45 cm

2. 27 cm

3. 30 cm

4. 33 cm

Answer

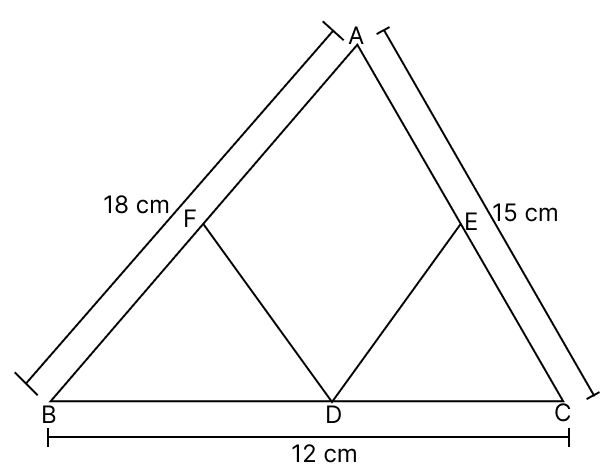
By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

Since, D and E are the mid-points of BC and AC respectively.

⇒ DE || AB and DE = $\dfrac{1}{2} AB = \dfrac{1}{2}$ × 18 = 9 cm

Since, F and D are the mid-points of AB and BC respectively.

⇒ FD || AC and FD = $\dfrac{1}{2} AC = \dfrac{1}{2}$ × 15 = 7.5 cm

AE = $\dfrac{1}{2}AC = \dfrac{1}{2} \times 15$ = 7.5 cm

AF = $\dfrac{1}{2}AB = \dfrac{1}{2} \times 18$ = 9 cm

Perimeter of AFED = AF + FD + DE + AE = 9 + 7.5 + 9 + 7.5 = 33 cm.

Hence, option 4 is the correct option.

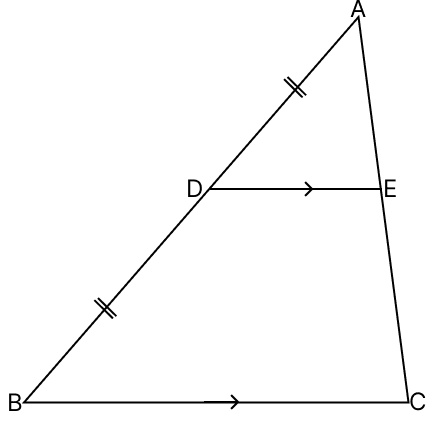
In the adjoining figure, AD = BD and DE || BC. If AC = 6 cm and DE = 4 cm, then the length of BC is :

1. 4 cm

2. 5 cm

3. 6 cm

4. 8 cm

Answer

Given,

D is the mid-point of AB.

By converse of mid-point theorem,

A line drawn through the midpoint of one side of a triangle, and parallel to another side, will bisect the third side.

In △ABC,

Since, D is the mid-point of AB and DE // BC, thus :

E is mid-point of AC.

By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

Since, D and E are the mid-points of AB and AC respectively.

DE || BC

⇒ DE = $\dfrac{1}{2}$ BC

⇒ BC = 2 DE

⇒ BC = 2 × 4

⇒ BC = 8 cm.

Hence, option 4 is the correct option.

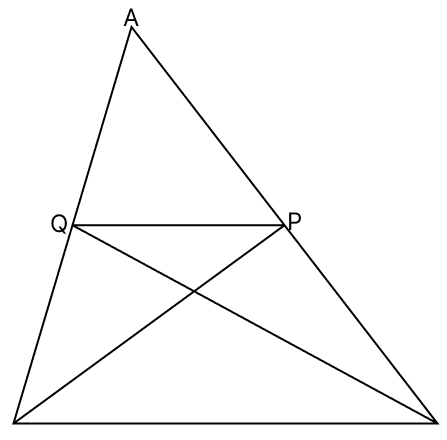
In the given figure, BP and CQ are two medians of the △ABC. If BC = 12 cm, the length of QP =

1. 4 cm

2. 6 cm

3. 8 cm

4. 10 cm

Answer

We know that,

Median drawn from the vertex bisects the opposite side.

Since, CQ is the median to AB.

⇒ AQ = BQ

Since, BP is the median to AC

⇒ AP = CP

By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

Since, Q and P are the mid-points of AB and AC respectively.

⇒ QP || BC and QP = $\dfrac{1}{2}$ BC

⇒ QP = $\dfrac{1}{2}$ × 12

⇒ QP = 6 cm.

Hence, option 2 is the correct option.

In △ABC, E is the mid-point of the median AD. BE is joined and produced to meet AC at F. Then, AF = ....AC.

1. 3

2. 2

3. $\dfrac{1}{3}$

4. $\dfrac{1}{2}$

Answer

Draw DY parallel to BF.

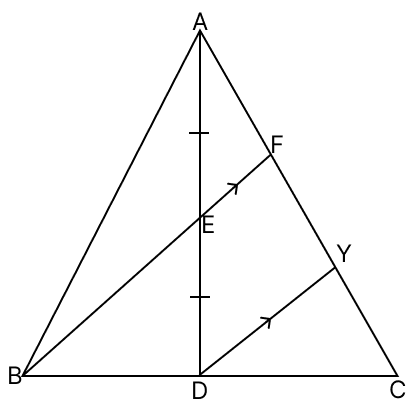
Since, BF || DY so, EF || DY

By converse of mid-point theorem,

A line drawn through the midpoint of one side of a triangle, and parallel to another side, will bisect the third side.

In △ADY,

Since, E is the mid-point of AD and EF || DY

⇒ F is the mid-point of AY.

∴ AF = FY

Given,

AD is the median.

In △BCF,

Since, D is the mid-point of BC and BF || DY

⇒ Y is the mid-point of FC.

∴ FY = CY

⇒ AF = FY = CY

From figure,

AC = AF + FY + CY = AF + AF + AF = 3 AF

⇒ AF = $\dfrac{1}{3}$ AC

Hence, option 3 is the correct option.

In the trapezium ABCD, AB || DC and AB > DC. P and Q are the mid-points of the diagonals AC and BD. Then, PQ || AB and PQ = .....(AB - DC).

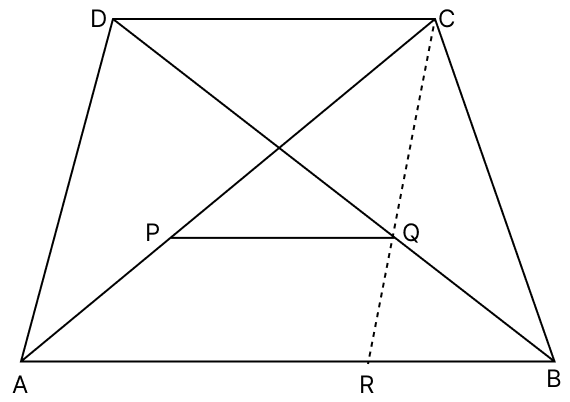
1. 2

2. 3

3. $\dfrac{1}{2}$

4. $\dfrac{1}{3}$

Answer

In △BQR and △CQD,

⇒ ∠BQR = ∠CQD (Vertically opposite angles are equal)

⇒ ∠BRQ = ∠QCD (Alternate angles are equal)

⇒ BQ = DQ (Q is the mid-point of BD)

∴ △BQR ≅ △CQD

⇒ BR = DC (Corresponding parts of congruent triangles are equal)

⇒ QR = CQ (Corresponding parts of congruent triangles are equal)

Given,

AB || DC and PQ || AB

∴ PQ || AB || DC

In △ARC,

Since, P and Q are the mid-points of AC and CR respectively.

By mid-point theorem,

⇒ PQ = $\dfrac{1}{2}$ AR

⇒ PQ = $\dfrac{1}{2}$ (AB - BR)

⇒ PQ = $\dfrac{1}{2}$ (AB - DC) (∵ BR = DC)

Hence, option 3 is the correct option.

Case Study

Ankita took part in a Rangoli Competition. She made a beautiful Rangoli in the shape of a triangle ABC as shown. In the triangle, P, Q and R are mid-points of the sides AB, BC and CA respectively. She decorated it by putting a garland along the sides of △PQR. The lengths of the sides of the triangle are AB = 20 cm, BC = 26 cm and AC = 24 cm.

Based on this information, answer the following questions:

1. The length of AP is :
   (a) QB
   (b) QR
   (c) AR
   (d) RP

2. The length of PQ is :
   (a) 12 cm
   (b) 13 cm
   (c) 10 cm
   (d) 15 cm

3. The length of the garland is :
   (a) 30 cm
   (b) 32 cm
   (c) 35 cm
   (d) 40 cm

4. Area of △PQR is :
   (a) area of △ABC
   
   (b) $\dfrac{1}{2}$ area of △ABC
   
   (c) $\dfrac{1}{3}$ area of △ABC
   
   (d) $\dfrac{1}{4}$ area of △ABC
   
   

5. APQR is a :
   (a) Rectangle
   (b) Parallelogram
   (c) Square
   (d) Rhombus

Answer

1. Given,

P is the mid-point of AB.

⇒ AP = $\dfrac{1}{2}$ AB ..........(1)

By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

Since, Q and R are the mid-points of BC and AC respectively.

⇒ QR = $\dfrac{1}{2}$ AB ........(2)

From equation (1) and (2), we get :

⇒ AP = QR

Hence, option (b) is the correct option.

2. By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

Since, P and Q are the mid-points of AB and BC respectively.

PQ || AC

⇒ PQ = $\dfrac{1}{2} AC = \dfrac{1}{2}$ × 24 = 12 cm.

Hence, option (a) is the correct option.

3. By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

Since, P and Q are the mid-points of AB and BC respectively.

PQ || AC

⇒ PQ = $\dfrac{1}{2} AC = \dfrac{1}{2}$ × 24 = 12 cm.

Since, P and R are the mid-points of AB and AC respectively.

PR || BC

⇒ PR = $\dfrac{1}{2}BC = \dfrac{1}{2}$ × 26 = 13 cm.

Since, R and Q are the mid-points of AC and BC respectively.

QR || AB

⇒ QR = $\dfrac{1}{2} AB = \dfrac{1}{2}$ × 20 = 10 cm.

Length of the garland = PQ + QR + PR = 12 + 10 + 13 = 35 cm.

Hence, option (c) is the correct option.

4. By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

In △ARP and △PQR,

Since, R and Q are the mid-points of AC and BC respectively.

QR || AB

⇒ QR || AP

Since, P and Q are the mid-points of AB and BC respectively.

PQ || AC

⇒ PQ || AR

⇒ ∠ARP = ∠QPR (Alternate angles are equal)

⇒ ∠APR = ∠QRP (Alternate angles are equal)

⇒ PR = PR (Common side)

∴ △ARP ≅ △PQR (By A.S.A axiom) ...(1)

In △QRC and △PQR,

⇒ ∠CRQ = ∠PQR (Alternate angles)

⇒ ∠CQR = ∠PRQ (Alternate angles)

⇒ QR = QR (Common side)

∴ △QRC ≅ △PQR (By A.S.A axiom) ...(2)

In △PBQ and △PQR,

Since, R and Q are the mid-points of AC and BC respectively.

QR || AB

⇒ QR || AP

Since, P and Q are the mid-points of AB and BC respectively.

PQ || AC

⇒ PQ || AR

⇒ ∠BPQ = ∠PQR (Alternate angles)

⇒ ∠BQP = ∠QPR (Alternate angles)

⇒ PQ = PQ (Common side)

∴ △PBQ ≅ △PQR (By A.S.A axiom) ...(3)

From eq.(1), (2) and (3), we have:

Area of △PBQ = Area of △QRC = Area of △ARP = Area of △PQR

From figure,

⇒ Area of △ABC = Area of △PBQ + Area of △QRC + Area of △ARP + Area of △PQR

⇒ Area of △ABC = Area of △PQR + Area of △PQR + Area of △PQR + Area of △PQR

⇒ Area of △ABC = 4 Area of △PQR

⇒ Area of △PQR = $\dfrac{1}{4}$ Area of △ABC

Hence, option (d) is the correct option.

5. By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

In △ARP and △PQR,

Since, R and Q are the mid-points of AC and BC respectively.

QR || AB

⇒ QR || AP

⇒ QR = $\dfrac{1}{2}AB$

⇒ QR = AP (∵ P is the midpoint of AB)

Since, P and Q are the mid-points of AB and BC respectively.

PQ || AC

⇒ PQ || AR

⇒ PQ = $\dfrac{1}{2}AC$

⇒ PQ = AR (∵ R is the midpoint of AC)

Since, in quadrilateral APQR opposite sides are parallel and equal.

∴ APQR is a parallelogram.

Hence, option (b) is the correct option.

Assertion (A): In the figure, if AD = DC = 4 cm, EC = 10 cm and DE || AB, then CE = 5 cm.

Reason (R): The straight line drawn through the mid-point of one side of a triangle parallel to other, bisects the third side.

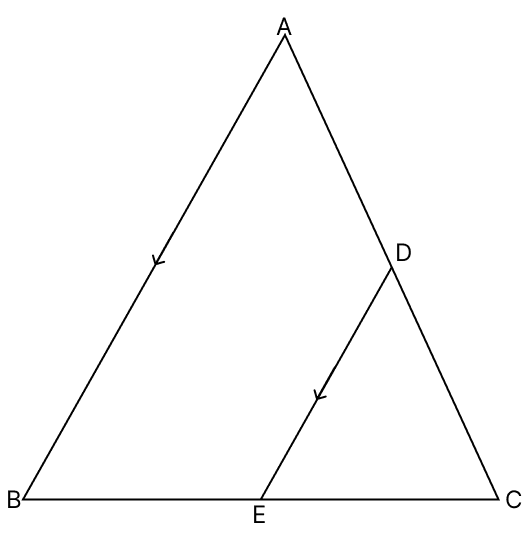
1. A is true, R is false

2. A is false, R is true

3. Both A and R are true

4. Both A and R are false

Answer

By converse of mid-point theorem,

A line drawn through the midpoint of one side of a triangle, and parallel to another side, will bisect the third side.

∴ Reason (R) is true.

In △ABC,

Since, D is the mid-point of AC and DE // AB, thus C is mid-point of BC.

CE = BE

From figure,

BC = CE + BE = CE + CE = 2 CE

⇒ CE = $\dfrac{1}{2}BC = \dfrac{1}{2}$ × 10 = 5 cm.

∴ Assertion (A) is true.

Hence, option 3 is the correct option.

Assertion (A): The mid-points of the sides of a quadrilateral ABCD are joined in order to get quadrilateral PQRS. PQRS is a rhombus.

Reason (R): Adjacent sides of a rhombus are equal and perpendicular to each other.

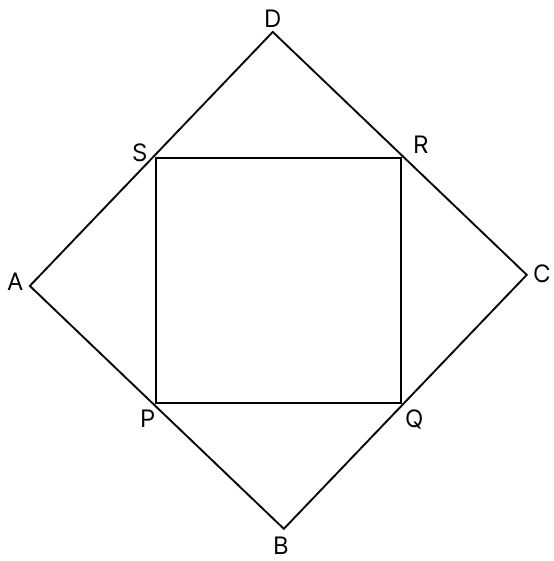
1. A is true, R is false

2. A is false, R is true

3. Both A and R are true

4. Both A and R are false

Answer

Join AC and BD.

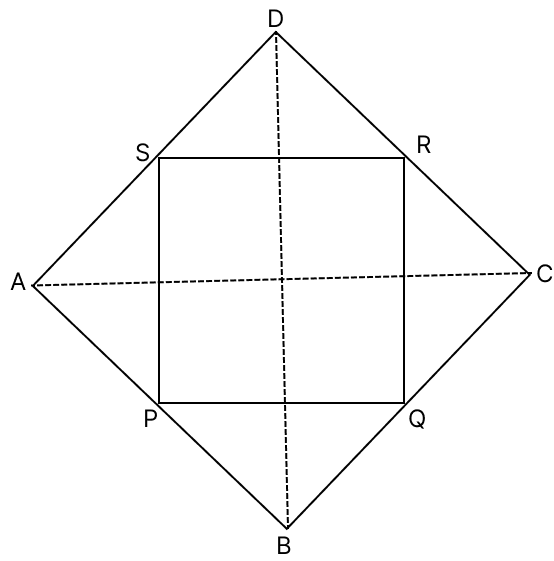
By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

In △ABC,

P and Q are midpoints of AB and BC respectively.

∴ PQ || AC and PQ = $\dfrac{1}{2}$ AC (By midpoint theorem) .....(1)

Similarly in △ADC,

S and R are midpoints of AD and CD respectively.

∴ RS || AC and RS = $\dfrac{1}{2}$ AC (By midpoint theorem) .....(2)

In △ABD,

P and S are midpoints of AB and AD respectively.

∴ PS || BD and PS = $\dfrac{1}{2}$ BD (By midpoint theorem) .....(3)

Similarly in △BCD,

Q and R are midpoints of BC and CD respectively.

∴ QR || BD and QR = $\dfrac{1}{2}$ BD (By midpoint theorem) .....(4)

From (1) and (2) we get,

PQ = RS and PQ || RS

From (3) and (4) we get,

PS = QR and PS || QR

Since, opposite sides are parallel and equal.

Thus, PQRS is a parallelogram.

∴ Assertion (A) is false.

In rhombus, adjacent sides are equal and adjacent angles are supplementary.

∴ Reason (R) is false.

Hence, option 4 is the correct option.

The figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order is a square only, if :

1. ABCD is a rhombus

2. Diagonals of ABCD are equal

3. Diagonals of ABCD are equal and perpendicular

4. Diagonals of ABCD are perpendicular

Answer

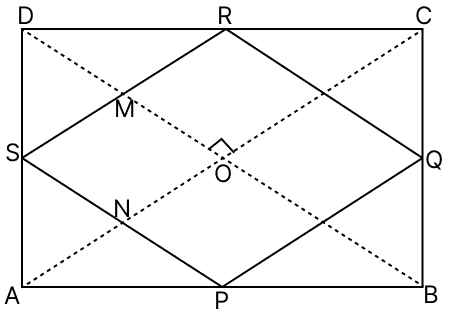
Let ABCD be a quadrilateral with P, Q, R and S as mid-points of AB, BC, CD and DA respectively.

Let diagonals be of equal length i.e, AC = BD = x and AC ⊥ BD.

In △BCA,

P and Q are mid-points of AB and BC respectively.

∴ PQ || AC and PQ = $\dfrac{1}{2} AC = \dfrac{1}{2}x$ [By mid-point theorem] ...(1)

Similarly in △ACD,

S and R are mid-points of AD and CD respectively.

∴ SR || AC and SR = $\dfrac{1}{2}AC = \dfrac{1}{2}x$ [By mid-point theorem] ...(2)

In △ABD,

S and P are mid-points of AD and AB respectively.

∴ SP || BD and SP = $\dfrac{1}{2}BD = \dfrac{1}{2}x$ [By mid-point theorem] ...(3)

Similarly in △BCD,

Q and R are mid-points of BC and CD respectively.

∴ QR || BD and QR = $\dfrac{1}{2}BD = \dfrac{1}{2}x$ [By mid-point theorem] ...(4)

From eq.(1), (2), (3) and (4), we have:

PQ = SR = SP = QR

∴ PQRS is a rhombus.

Since, SP || BD and AC ⊥ BD

∴ SP ⊥ AC

⇒ SN ⊥ AC

⇒ ∠SNO = 90°

Since, SR || AC and AC ⊥ BD

∴ SR ⊥ BD

⇒ SM ⊥ BD

⇒ ∠SMO = 90°

From figure,

⇒ ∠MOC + ∠MON = 180° [Linear pair]

⇒ 90° + ∠MON = 180°

⇒ ∠MON = 180° - 90° = 90°.

In quadrilateral sum of angles = 360°

⇒ ∠O + ∠M + ∠N + ∠S = 360°

⇒ 90° + 90° + 90° + ∠S = 360°

⇒ 270° + ∠S = 360°

⇒ ∠S = 360° - 270°

⇒ ∠S = 90°.

Since, in rhombus adjacent angles sum = 180°

Thus, in rhombus PQRS.

⇒ ∠S + ∠R = 180°

⇒ 90° + ∠R = 180°

⇒ ∠R = 180° - 90°

⇒ ∠R = 90°.

⇒ ∠Q + ∠R = 180°

⇒ 90° + ∠Q = 180°

⇒ ∠Q = 180° - 90°

⇒ ∠Q = 90°.

⇒ ∠S + ∠P = 180°

⇒ 90° + ∠P = 180°

⇒ ∠P = 180° - 90°

⇒ ∠P = 90°.

Since, PQ = QR = RS = SP and ∠P = ∠Q = ∠R = ∠S = 90°.

∴ PQRS is a square.

Thus, we can say that :

The figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only if diagonals of ABCD are equal and perpendicular.

Hence, option 3 is the correct option.

D and E are the mid-points of the sides AB and AC respectively of △ABC. DE is produced to F. To show that CF is equal and parallel to DA, we need an additional information, which is :

1. DE = EF

2. AE = EF

3. ∠DAE = ∠EFC

4. ∠ADE = ∠ECF

Answer

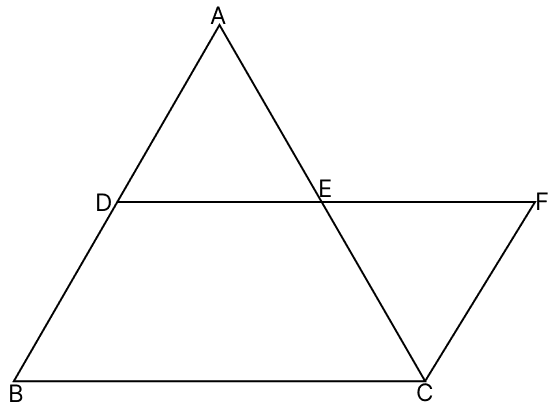
Assume that, DE = EF

In △ADE and △CFE,

⇒ AE = CE

⇒ DE = EF

⇒ ∠AED = ∠CEF (Vertically opposite angles are equal)

∴ △ADE ≅ △CFE (S.A.S. axiom)

⇒ DA = CF (Corresponding parts of congruent triangles are equal)

⇒ ∠DAE = ∠ECF ..(1) (Corresponding parts of congruent triangles are equal)

⇒ ∠ADE = ∠EFC ..(2) (Corresponding parts of congruent triangles are equal)

Since, ∠DAE and ∠ECF are alternate angles and since they are equal, thus DA // CF.

Thus, if DE = EF then DA is equal and parallel to CF.

Hence, option 1 is the correct option.

In which of the following cases you will get 2XY = QR for the given figure?

(i) When PX = QX and PY = RY

(ii) When PX = QX and a + b = 180°

1. Only in case (i)

2. Only in case (ii)

3. In both the cases

4. None of these

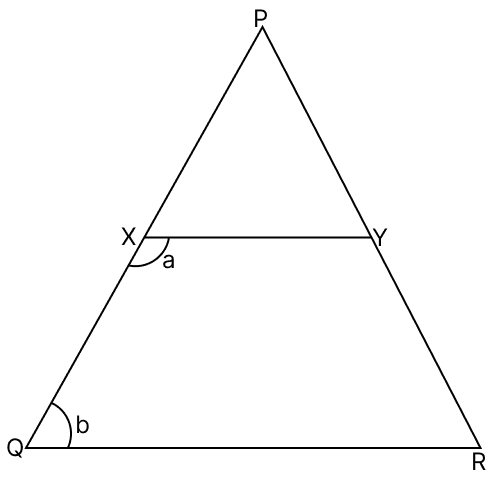
Answer

In case (i) :

By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

In △PQR,

Given,

PX = QX and PY = RY

⇒ X and Y are midpoints of PQ and PR respectively.

∴ XY || QR and XY = $\dfrac{1}{2}$ QR

⇒ QR = 2 XY

∴ Case (i) is true.

In case (ii) :

Given,

PX = QX

⇒ X is the mid-point of PQ

By converse of mid-point theorem,

A line drawn through the midpoint of one side of a triangle, and parallel to another side, will bisect the third side.

Given,

⇒ ∠QXY + ∠XQR = 180°

⇒ a + b = 180°

⇒ ∠QXY and ∠XQR are co-interior angles and their sum is equal to 180°.

∴ XY is parallel to QR.

In △PQR,

Since, X is the mid-point of PQ and XY // QR, thus :

Y is mid-point of PR.

Since, X and Y are mid-points of side PQ and PR respectively.

⇒ XY = $\dfrac{1}{2}$ QR (By mid-point theorem)

⇒ QR = 2 XY

∴ Case (ii) is true.

Hence, option 3 is the correct option.

In the figure, R is the mid-point of AB, P is the mid-point of AR and L is the mid-point of AP. If RS, PQ and LM are parallel to each other, then the length of BC is :

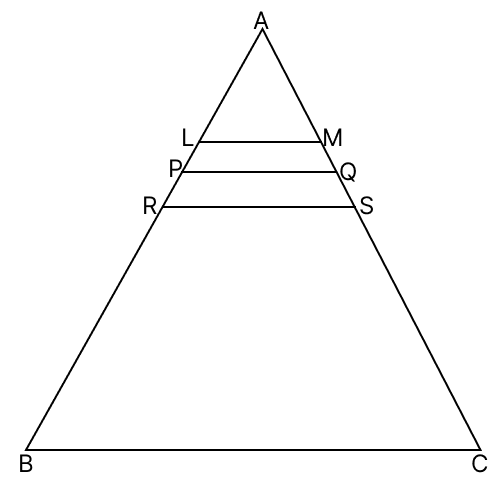
1. 3 LM

2. 4 LM

3. 6 LM

4. 8 LM

Answer

By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

By converse of mid-point theorem,

A line drawn through the midpoint of one side of a triangle, and parallel to another side, will bisect the third side.

In △APQ,

Given,

AL = LP and LM || PQ

∴ M is mid-point of AQ (By converse of mid-point theorem)

⇒ L and M are midpoints of AP and AQ respectively.

∴ LM = $\dfrac{1}{2}$ PQ

⇒ PQ = 2 LM ......(1)

In △ARS,

Given,

AP = RP and PQ || RS

∴ Q is mid-point of AS (By converse of mid-point theorem)

⇒ P and Q are midpoints of AR and AS respectively.

∴ PQ = $\dfrac{1}{2}$ RS .........(2)

From equation (1) and (2), we get :

⇒ 2 LM = $\dfrac{1}{2}$ RS

⇒ RS = 4 LM ....(3)

In △ABC,

Given,

AR = BR

⇒ RS || BC and S is the mid-point of AC. (By converse of mid-point theorem)

∴ RS = $\dfrac{1}{2}$ BC (By mid-point theorem)

Substituting value of RS in equation (3), we get:

⇒ $\dfrac{1}{2}$ BC = 4 LM

⇒ BC = 8 LM.

Hence, option 4 is the correct option.

In the given figure, △ABC is a scalene triangle in which ∠B = 90°. P is the mid-point of AB, PQ || BC and QM ⊥ BC. Which type of quadrilateral is PQMB?

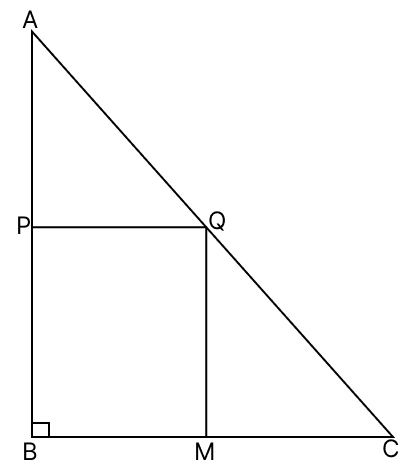
Answer

Given,

∠B = 90° and PQ || BC

AB is the transversal.

⇒ ∠PBM = ∠APQ = 90° (Corresponding angles are equal)

⇒ ∠APQ + ∠BPQ = 180° (Linear pair)

⇒ 90° + ∠BPQ = 180°

⇒ ∠BPQ = 180° - 90°

⇒ ∠BPQ = 90°

Since, QM ⊥ BC

⇒ ∠QMB = 90°

In a quadrilateral PQMB,

⇒ ∠PBM + ∠BPQ + ∠QMB + ∠PQM = 360°

⇒ 90° + 90° + 90° + ∠PQM = 360°

⇒ 270° + ∠PQM = 360°

⇒ ∠PQM = 360° - 270°

⇒ ∠PQM = 90°.

All the angles of a quadrilateral = 90°

By converse of mid-point theorem,

A line drawn through the midpoint of one side of a triangle, and parallel to another side, will bisect the third side.

In △ABC,

Since, P is the mid-point of AB and PQ || BC, thus :

Q is mid-point of AC.

In △ABC,

Since, Q is the mid-point of AC and QM || AB (as both are perpendicular to BC), thus :

Mi si mid-point of BC.

In △ABC,

Since, Q and M are mid-points of AC and BC respectively.

⇒ QM = $\dfrac{1}{2}$ AB (By mid-point theorem)

⇒ QM = PB ...(1)

In △ABC,

Since, P and Q are mid-points of AB and AC respectively.

⇒ PQ = $\dfrac{1}{2}$ BC (By mid-point theorem)

⇒ PQ = BM ...(2)

From eq.(1) and (2), we have :

Since, opposite sides are equal and all the interior angles equals to 90°.

∴ PQMB is a rectangle.

Hence, PQMB is a rectangle.

In the given figure, A, B, C and D are mid-points of PQ, QR, RS and PS respectively. E, F, G and H are mid-points of AB, BC, CD and AD respectively. Which type of quadrilaterals are ABCD and EFGH?

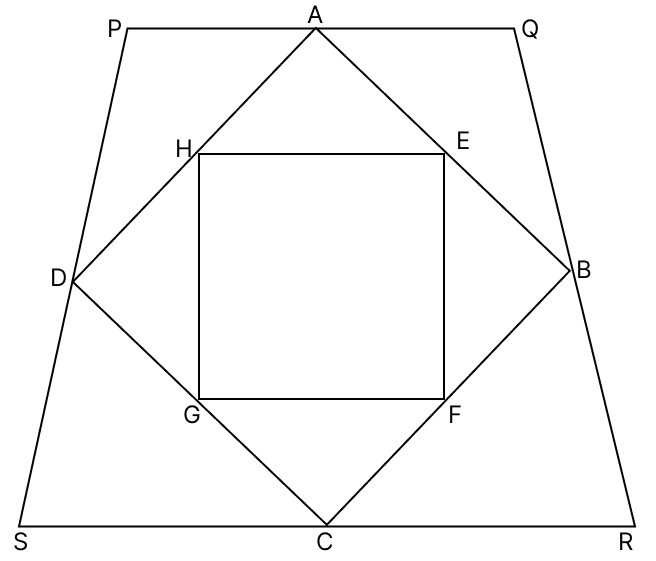
Answer

Join QS, PR, AC and BD.

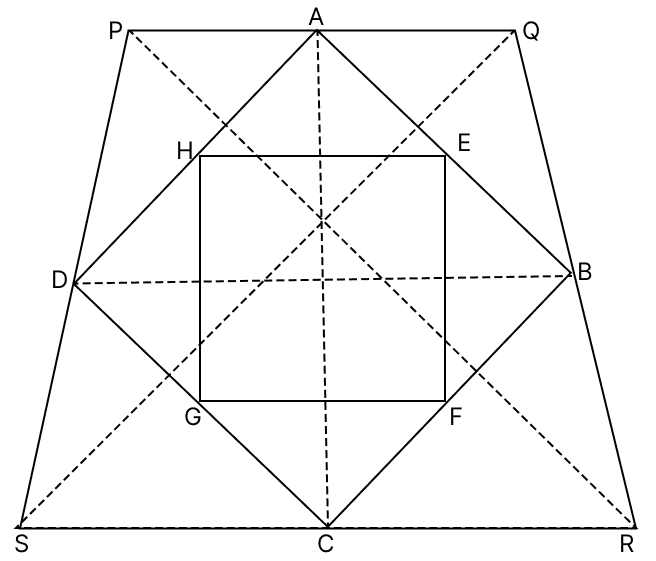
By mid-point theorem,

The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is equal to half of it.

In △QRP,

A and B are midpoints of PQ and QR respectively.

∴ AB || PR and AB = $\dfrac{1}{2}$ PR (By midpoint theorem) .....(1)

Similarly in △PRS,

D and C are midpoints of PS and RS respectively.

∴ DC || PR and DC = $\dfrac{1}{2}$ PR (By midpoint theorem) .....(2)

In △PQS,

D and A are midpoints of PS and PQ respectively.

∴ DA || QS and DA = $\dfrac{1}{2}$ QS (By midpoint theorem) .....(3)

Similarly in △QRS,

B and C are midpoints of QR and SR respectively.

∴ BC || QS and BC = $\dfrac{1}{2}$ QS (By midpoint theorem) .....(4)

From (1) and (2) we get,

AB = DC and AB || DC

From (3) and (4) we get,

DA = BC and DA || BC

Since, opposite sides are parallel and equal.

Thus, ABCD is a parallelogram.

In △ABC,

E and F are midpoints of AB and BC respectively.

∴ EF || AC and EF = $\dfrac{1}{2}$ AC (By midpoint theorem) .....(5)

Similarly in △ADC,

H and G are midpoints of AD and CD respectively.

∴ GH || AC and GH = $\dfrac{1}{2}$ AC (By midpoint theorem) .....(6)

In △ABD,

H and E are midpoints of AD and AB respectively.

∴ EH || BD and EH = $\dfrac{1}{2}$ BD (By midpoint theorem) .....(7)

Similarly in △BCD,

F and G are midpoints of BC and CD respectively.

∴ FG || BD and FG = $\dfrac{1}{2}$ BD (By midpoint theorem) .....(8)

From (5) and (6) we get,

EF = GH AND EF || GH

From (7) and (8) we get,

EH = FG and EH || FG

Since, opposite sides are parallel and equal.

Thus, EFGH is a parallelogram.

Hence, ABCD and EFGH are parallelograms.