Mathematics
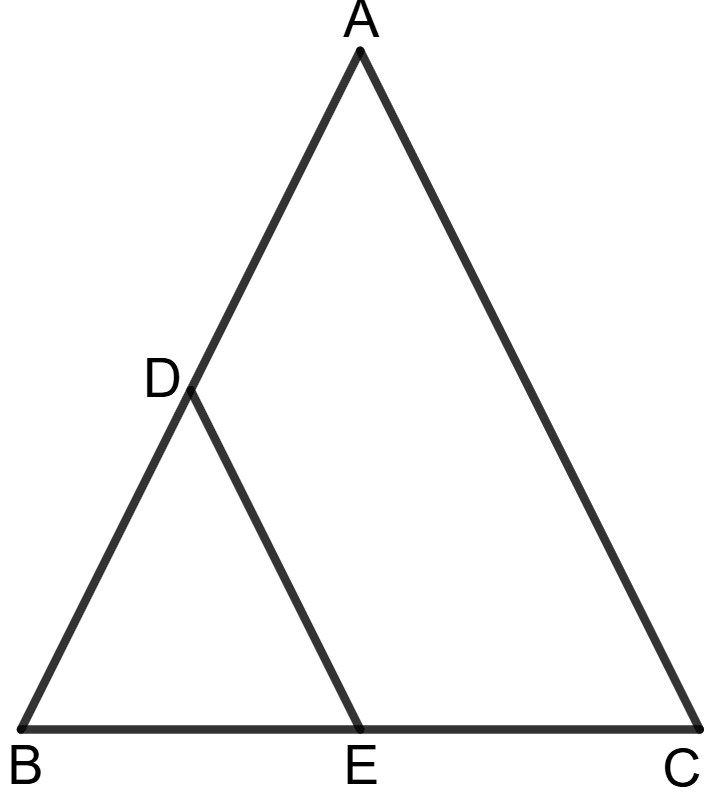
In △ ABC, D is mid-point of AB and E is mid-point of BC. Calculate :
(i) DE, if AC = 6.4 cm,
(ii) ∠DEB, if ∠ACB = 63°.
Mid-point Theorem
1 Like
Answer
(i) By the Midpoint Theorem, the line segment joining the midpoints of two sides of a triangle is parallel to the third side and is half of its length.
In △ ABC, since D is mid-point of AB and E is mid-point of BC.
So, DE = AC
DE = x 6.4 = 3.2 cm
Hence, the length of DE = 3.2 cm.
(ii) Since DE is parallel to AC (by mid-point theorem),
∠DEB = ∠ACB = 63° (∵ corresponding angles of parallel lines)
Hence, ∠DEB = 63°.
Answered By
2 Likes
Related Questions
In the following figure, AB = AD, AC = AE and ∠BAD = ∠CAE.
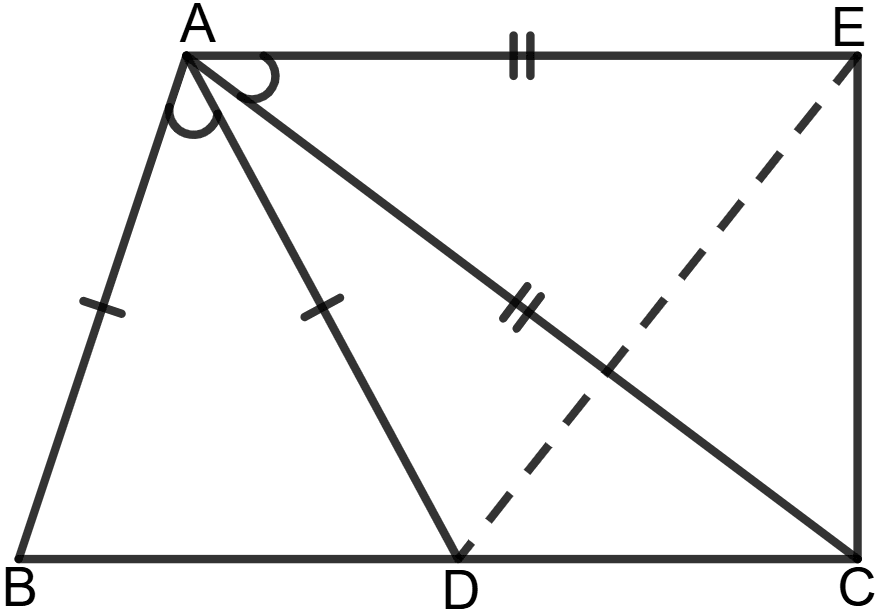
Prove that : BC = ED.
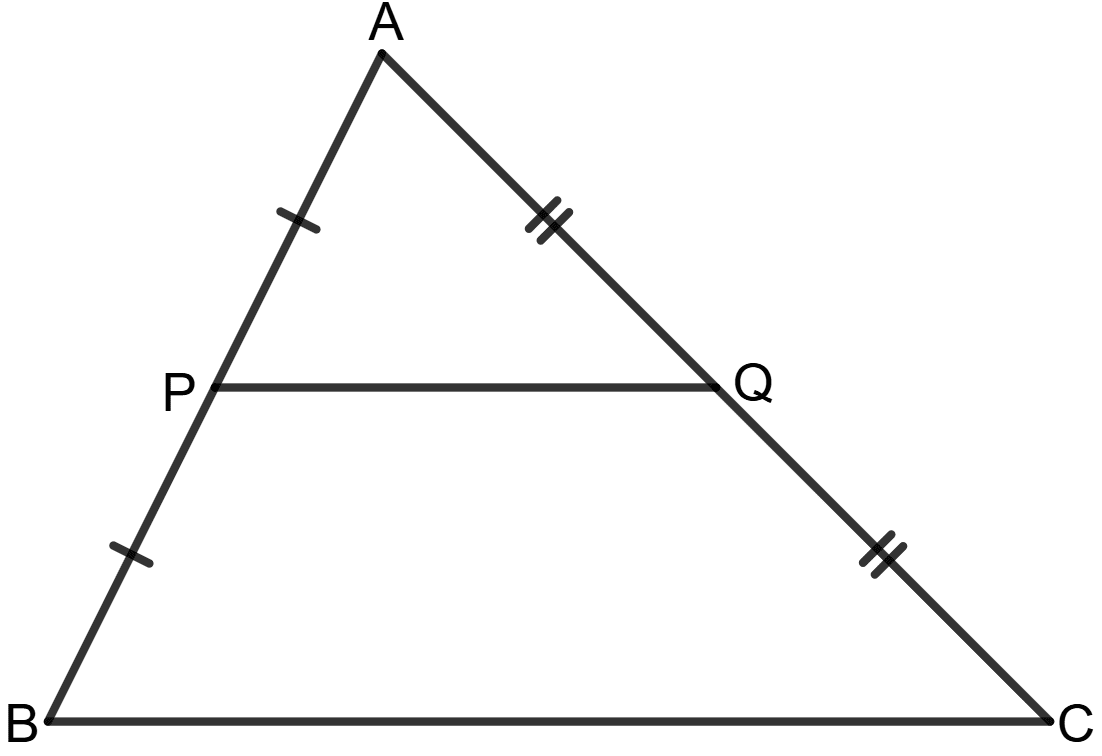
In triangle ABC, P is mid-point of AB and Q is mid-point of AC. If AB = 9.6 cm, BC = 11 cm and AC = 11.2 cm; find the perimeter of the trapezium PBCQ.
In △ ABC, D, E and F are mid-points of sides AB, BC and AC respectively. Prove that AE and DF bisect each other.
In a kite shaped figure ABCD, AB = AD and CB = CD. Points P, Q and R are mid-points of sides AB, BC and CD respectively.
Prove that :
(i) ∠PQR = 90°
(ii) Line through P and parallel to QR bisects side AD.