In a kite shaped figure ABCD, AB = AD and CB = CD. Points P, Q and R are mid-points of sides AB, BC and CD respectively.

Prove that :

(i) ∠PQR = 90°

(ii) Line through P and parallel to QR bisects side AD.

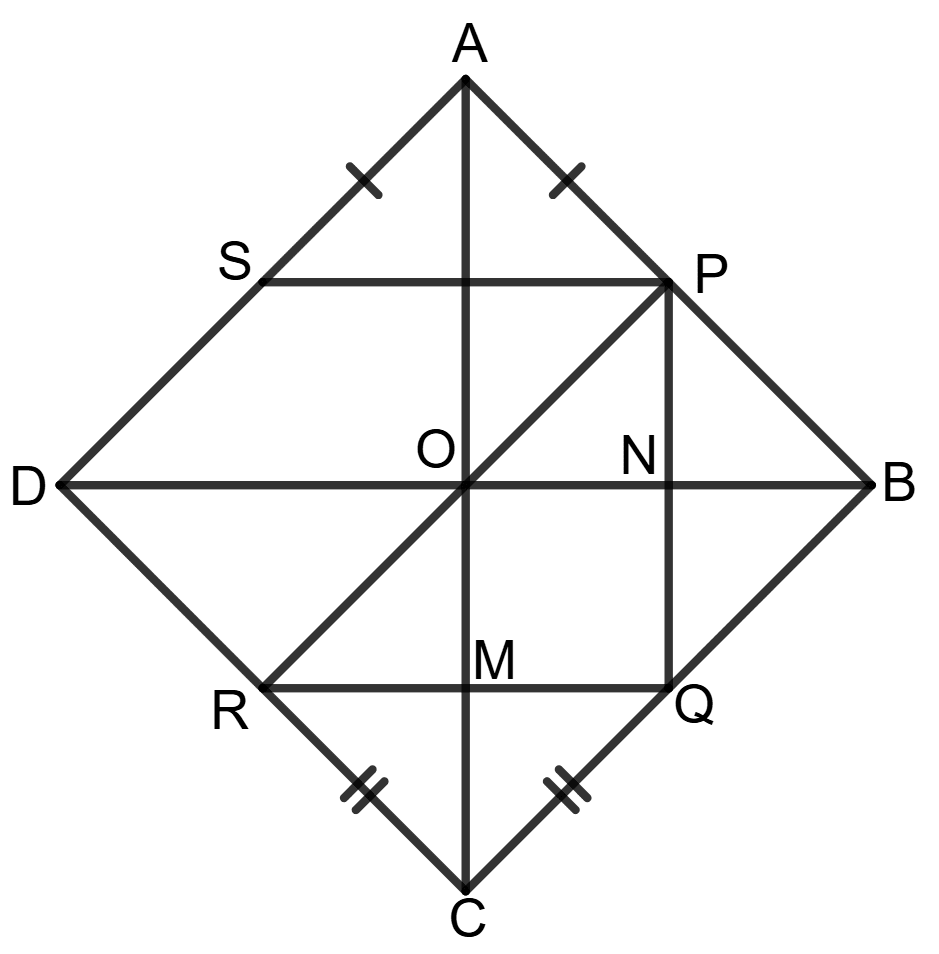
(i) Given: ABCD is a kite where AB = AD and CB = CD. Points P, Q and R are mid-points of sides AB, BC and CD, respectively.

To prove:

(i) ∠PQR = 90°

(ii) A line through P and parallel to QR bisects AD.

Construction: Join diagonals AC and BD.

Prove: In Δ ABC, P and Q are mid-points of AB and BC, respectively.

By midpoint theorem,

PQ ∥ AC and PQ = $\dfrac{1}{2}$ AC ……………….(1)

Similarly, in Δ BCD, Q and R are mid-points of BC and CD, respectively.

By midpoint theorem,

RQ ∥ DB and RQ = $\dfrac{1}{2}$ DB ……………….(2)

In a kite, the diagonals bisect each other at 90°.

So, ∠BOC = 90°

From (1) and (2), PQ ∥ AC and RQ ∥ DB.

Since diagonals AC and BD intersect at right angles and PQ ∥ AC and RQ ∥ DB, it follows that:

∠PQR = 90°

Hence, ∠PQR = 90°.

(ii) Construction: Extend the line through P such that it meets AD at S with PS // QR.

Since we already proved that PS ∥ QR and QR ∥ BD, we get:

⇒ PS ∥ BD

In Δ ABD, P is mid-point of AB and PS ∥ BD.

By the converse of midpoint theorem, S must be midpoint of AD.

Hence, the line through P parallel to QR bisects side AD.