In a scalene triangle ABC, AD and BE are medians. F is a point on AC so that DF//BE. Show that : AC = 4 x EF.

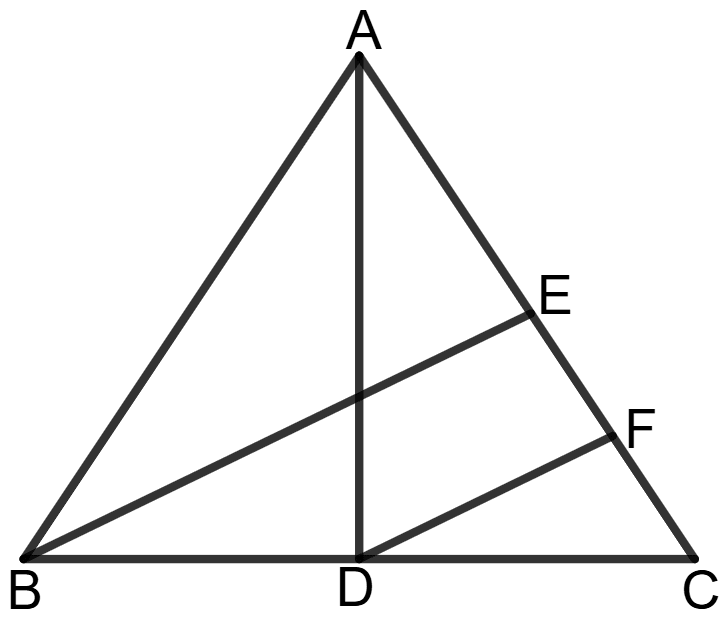
Given: In a scalene Δ ABC, AD and BE are medians. A point F is on AC such that DF//BE.

To prove: AC = 4 x EF

Construction: Join BE, DF and AD.

Proof: Since BE is a median, it divides AC into two equal parts:

∴ AE = EC = $\dfrac{1}{2}$ AC

In Δ BEC, BE ∥ DF and D is midpoint of BC.

By the converse of the midpoint theorem, since DF // BE and D is the midpoint of BC, F must be the midpoint of EC.

Since F is the midpoint of EC, we get:

∴ EF = FC = $\dfrac{1}{2}$ EC

⇒ EF = $\dfrac{1}{2} \times \dfrac{1}{2}$ AC

= $\dfrac{1}{4}$ AC

⇒ AC = 4 x EF

Hence, AC = 4 x EF.