Mathematics
ABC is an isosceles triangle with AB = AC = 13 cm and BC = 10 cm. Calculate the length of the perpendicular from A to BC.
Pythagoras Theorem
4 Likes
Answer
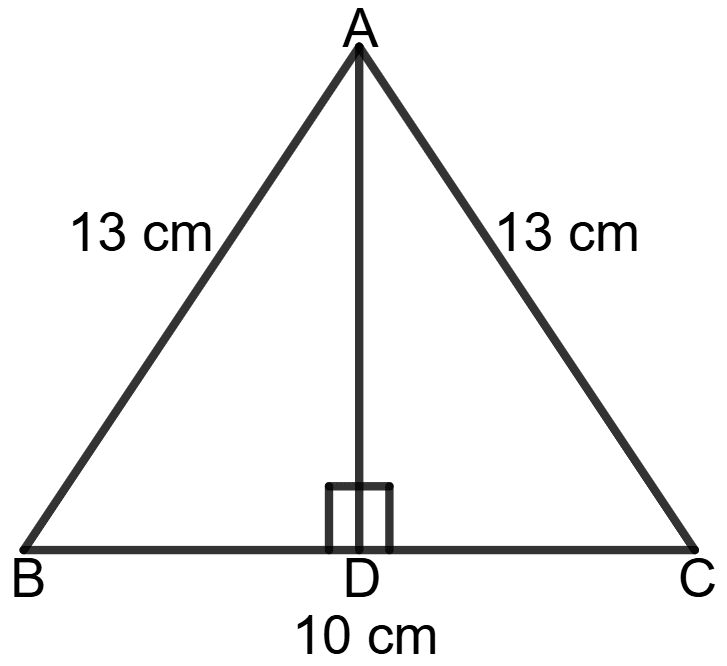
Given: AB = AC = 13 cm, BC = 10 cm.
Let D be the foot of the perpendicular from A to BC.
To Prove: The length of AD (perpendicular from A to BC).
Construction: Join AD.
Proof: Since Δ ABC is an isosceles triangle (AB = AC), the perpendicular AD from A to BC will bisect BC. Thus,
BD = DC = = 5 cm
In right-angled triangle ADB,
AB2 = AD2 + BD2
⇒ 132 = AD2 + 52
⇒ 169 = AD2 + 25
⇒ AD2 = 169 - 25
⇒ AD2 = 144
⇒ AD = = 12
Hence, the length of the perpendicular from A to BC is 12 cm.
Answered By
1 Like
Related Questions
In a scalene triangle ABC, AD and BE are medians. F is a point on AC so that DF//BE. Show that : AC = 4 x EF.
Show that the quadrilateral formed by joining the mid-points of the adjacent sides of a square, is also a square.
In triangle ABC, AB > AC. E is the mid-point of BC and AD is perpendicular to BC. Prove that :
AB2 + AC2 = 2AE2 + 2BE2
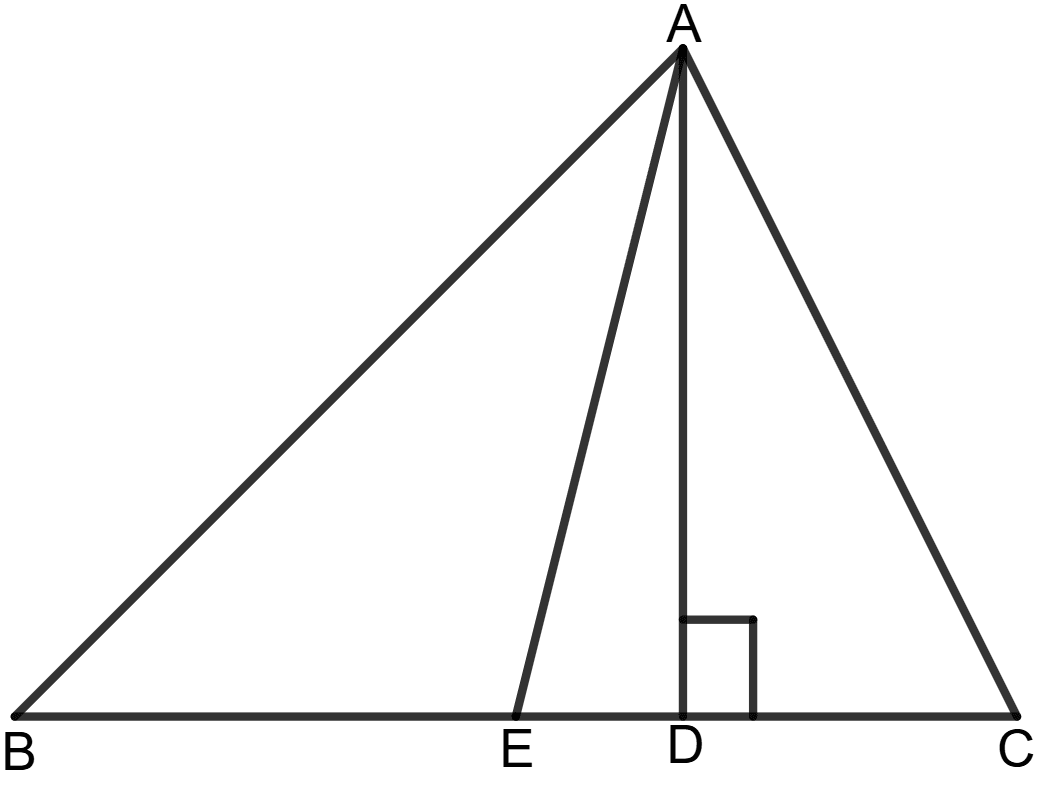
In the following figure :
OA = 2 cm = AB = 2BC = CD = DE
Find the length of OE.