Show that the quadrilateral formed by joining the mid-points of the adjacent sides of a square, is also a square.

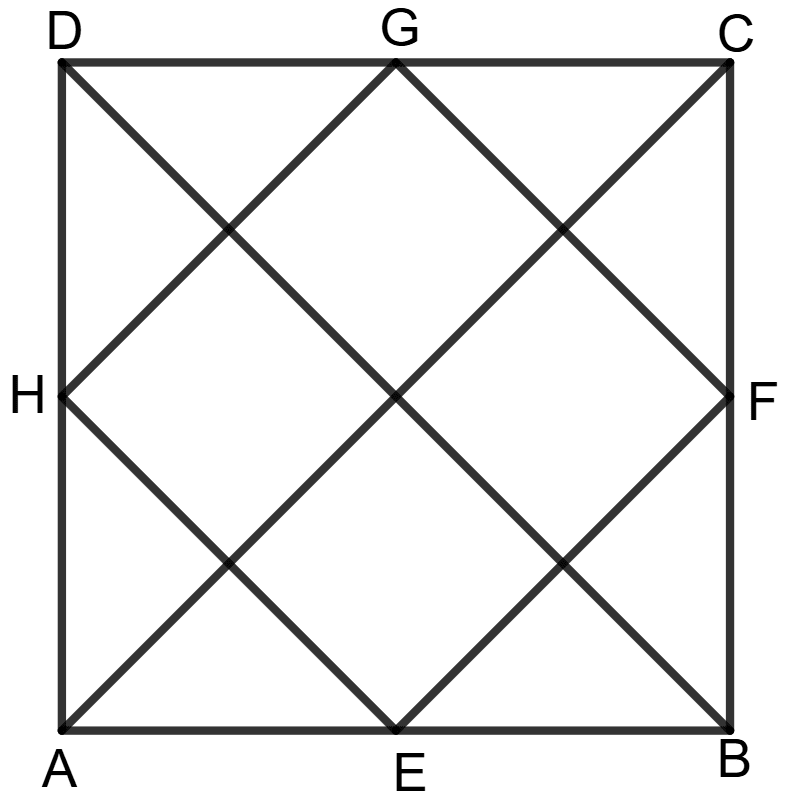
Given: ABCD is a square and E, F, G and H are midpoints of sides AB, BC, CD and DA respectively.

To prove: The quadrilateral EFGH is a square.

Construction: Join EF, FG, GH and HE to form quadrilateral EFGH. Also, draw the diagonals AC and BD of square ABCD.

Proof: In Δ ACD, G and H are the midpoints of CD and AD.

By the Midpoint Theorem:

GH ∥ AC and GH = $\dfrac{1}{2}$ AC ……………….(1)

Similarly, in Δ ABC, E and F are the midpoints of AB and BC.

By the Midpoint Theorem:

EF ∥ AC and EF = $\dfrac{1}{2}$ AC ……………….(2)

From (1) and (2), we get:

EF ∥ GH and EF = GH = $\dfrac{1}{2}$ AC ……………….(3)

Similarly, in Δ ABD, E and H are midpoints of AB and AD, so:

EH ∥ BD and EH = $\dfrac{1}{2}$ BD ……………….(4)

In Δ BCD, G and F are midpoints of CD and BC, so:

∴ FG ∥ BD and FG = $\dfrac{1}{2}$ BD ……………….(5)

From (4) and (5), we get:

EH ∥ FG and EH = FG = $\dfrac{1}{2}$ BD ……………….(6)

Since diagonals of a square are equal, we know:

AC = BD

Dividing both sides by 2, we get:

$\dfrac{AC}{2} = \dfrac{BD}{2}$

Substituting above value in equation (3) and (6),

EF = GH = EH = FG ……………….(7)

Since opposite sides are equal and parallel, EFGH is a parallelogram.

In Δ GOH and Δ GOF,

OH = OF (diagonals of parallelogram bisect each other)

GH = GF (from (7))

OG = OG (Common side)

By SSS Congruence,

Δ GOH ≅ Δ GOF

So, corresponding angles are equal:

∠GOH = ∠GOF (C.P.C.T.)

Since GOH and GOF are on a straight line:

⇒ ∠GOH + ∠GOF = 180°

⇒ ∠GOH + ∠GOH = 180°

⇒ 2∠GOH = 180°

⇒ ∠GOH = $\dfrac{180°}{2}$

⇒ ∠GOH = 90°

Thus, the diagonals of EFGH are perpendicular to each other, confirming that EFGH is a square.

Hence, the quadrilateral formed by joining the mid-points of the adjacent sides of a square, is also a square.