P, Q, R and S are the mid points of sides AB, BC, CD and DA respectively of rhombus ABCD. Show that PQRS is a rectangle.

Under what condition will PQRS be a square ?

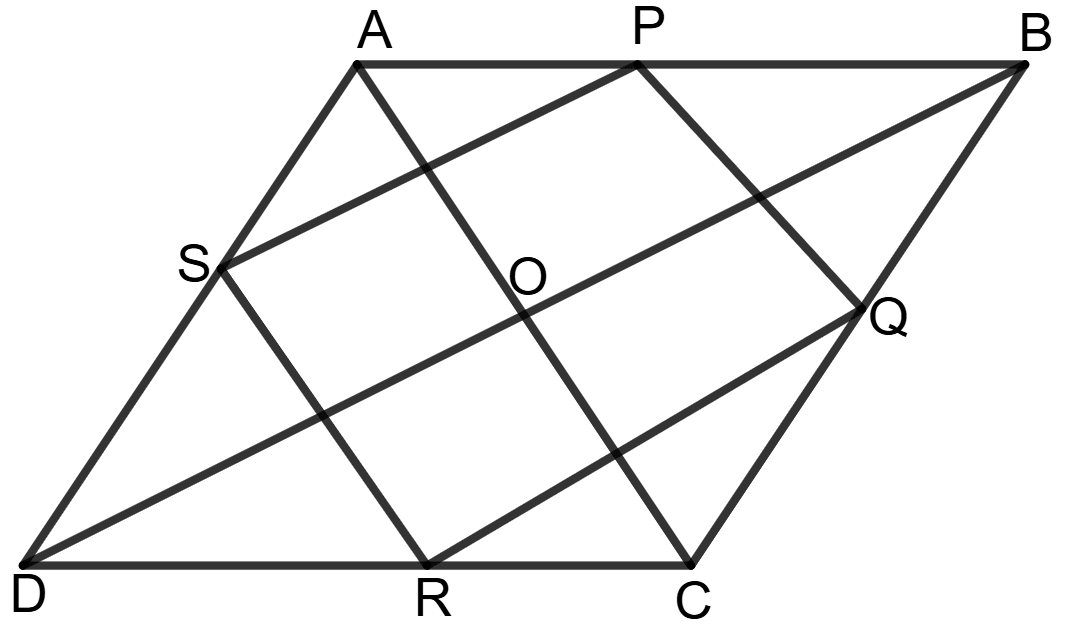
Given: In rhombus ABCD, P, Q, R and S are the mid points of sides AB, BC, CD and DA respectively.

To prove: PQRS is a rectangle.

Construction: Join PQ, QR, RS, and SP to form quadrilateral PQRS. Also, join diagonals AC and BD of rhombus ABCD.

Proof: Since ABCD is a rhombus, its diagonals AC and BD, bisect each other at right angles.

⇒ ∠AOD = ∠COD = ∠BOC = ∠AOB = 90°

In Δ ACD, S and R are the midpoints of AD and CD. By the midpoint theorem,

SR ∥ AC and SR = $\dfrac{1}{2}$ AC ……………….(1)

Similarly, in Δ ABC, P and Q are the midpoints of AB and BC. By the midpoint theorem,

PQ ∥ AC and PQ = $\dfrac{1}{2}$ AC ……………….(2)

From equations (1) and (2),

SR ∥ PQ and SR = PQ = $\dfrac{1}{2}$ AC ……………….(3)

In the same way, in Δ ABD, S and P are the midpoints of AD and AB. By the midpoint theorem,

SP ∥ BD and SP = $\dfrac{1}{2}$ BD ……………….(4)

Similarly, in Δ BDC, R and Q are the midpoints of DC and BC. By the midpoint theorem,

RQ ∥ BD and RQ = $\dfrac{1}{2}$ BD ……………….(5)

From equations (4) and (5),

SP ∥ RQ and SP = RQ = $\dfrac{1}{2}$ BD ……………(6)

Since opposite sides are equal and parallel, PQRS is a parallelogram.

Also, since diagonals of rhombus bisect each other at right angles, the midpoints P, Q, R, S form a quadrilateral where:

∠SPQ = ∠PQR = ∠QRS = ∠RSP = 90°

Thus, PQRS is a rectangle.

For PQRS to be a square, it must be a rectangle with all sides equal:

PQ = QR = RS = SP

From the Midpoint Theorem, we know:

PQ = $\dfrac{1}{2}$ AC, QR = $\dfrac{1}{2}$ BD

For PQRS to be a square, we must have:

$\dfrac{1}{2}$ AC = $\dfrac{1}{2}$ BD

⇒ AC = BD

Since AC and BD are diagonals of rhombus ABCD, AC = BD is only true when ABCD is a square.

Thus, PQRS is a square if and only if ABCD is a square.

Hence, PQRS is a rectangle and PQRS will be a square when ABCD is a square.