Mathematics
ABC is an isosceles triangle with AB = AC = 12 cm and BC = 8 cm. The area of the triangle is :
cm2
cm2
cm2
cm2
Pythagoras Theorem
22 Likes
Answer
Let AD be the altitude.
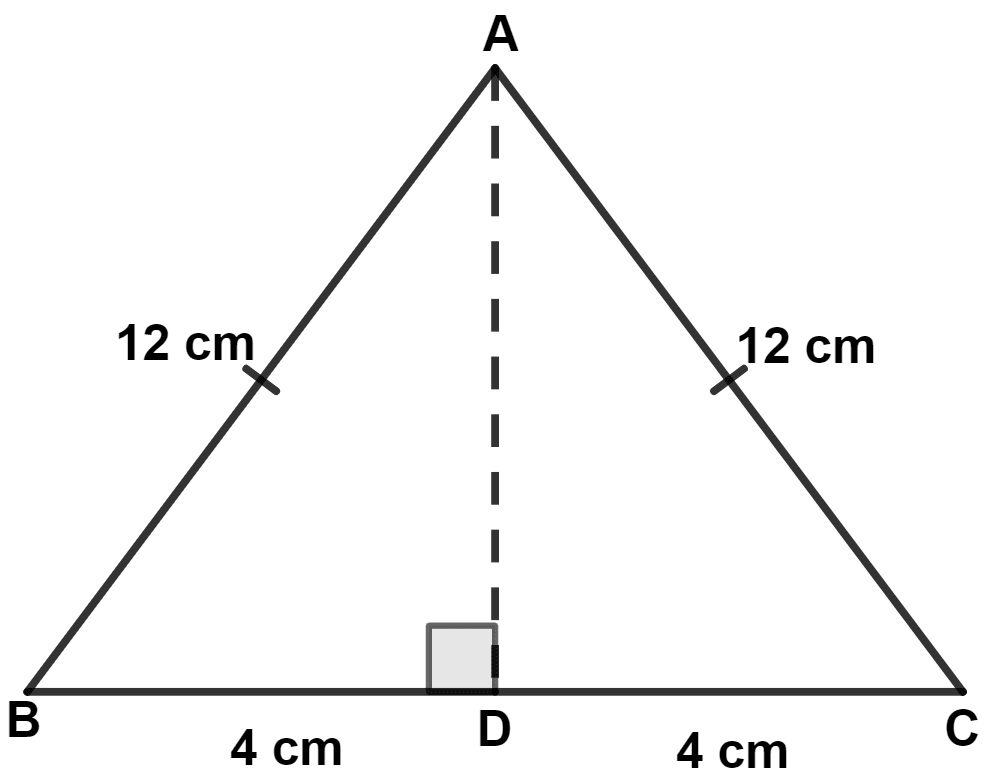
In an isosceles triangle, the altitude from the vertex bisects the base.
∴ BD = CD = = 4 cm.
In right angle triangle ABD,
By pythagoras theorem,
⇒ (Hypotenuse)2 = (Perpendicular)2 + (Base)2
⇒ AB2 = AD2 + BD2
⇒ 122 = AD2 + 42
⇒ 144 = AD2 + 16
⇒ AD2 = 144 - 16
⇒ AD2 = 128
⇒ AD = cm.
Area of right angle triangle = × base × height
From figure,
⇒ Area of △ ABC = Area of △ ABD + Area of △ ACD
⇒ Area of △ ABC =
⇒ Area of △ ABC
Hence, Option 1 is the correct option.
Answered By
17 Likes
Related Questions
If the lengths of the sides of a triangle are in the ratio 5 : 12 : 13; then the triangle is :
acute-angled triangle
scalene triangle
scalene right-angled triangle
obtuse-angled triangle
In a right-angled triangle, hypotenuse is 10 cm and the ratio of the other two sides is 3 : 4, the sides are :
6 cm and 4 cm
8 cm and 6 cm
3 cm and 4 cm
8 cm and 4 cm
In a rhombus, its diagonals are 30 cm and 40 cm, its perimeter is :
20 cm
10 cm
60 cm
100 cm
In the given figure, AD = 13 cm, DC = 12 cm and BC = 3 cm, then AB is equal to :
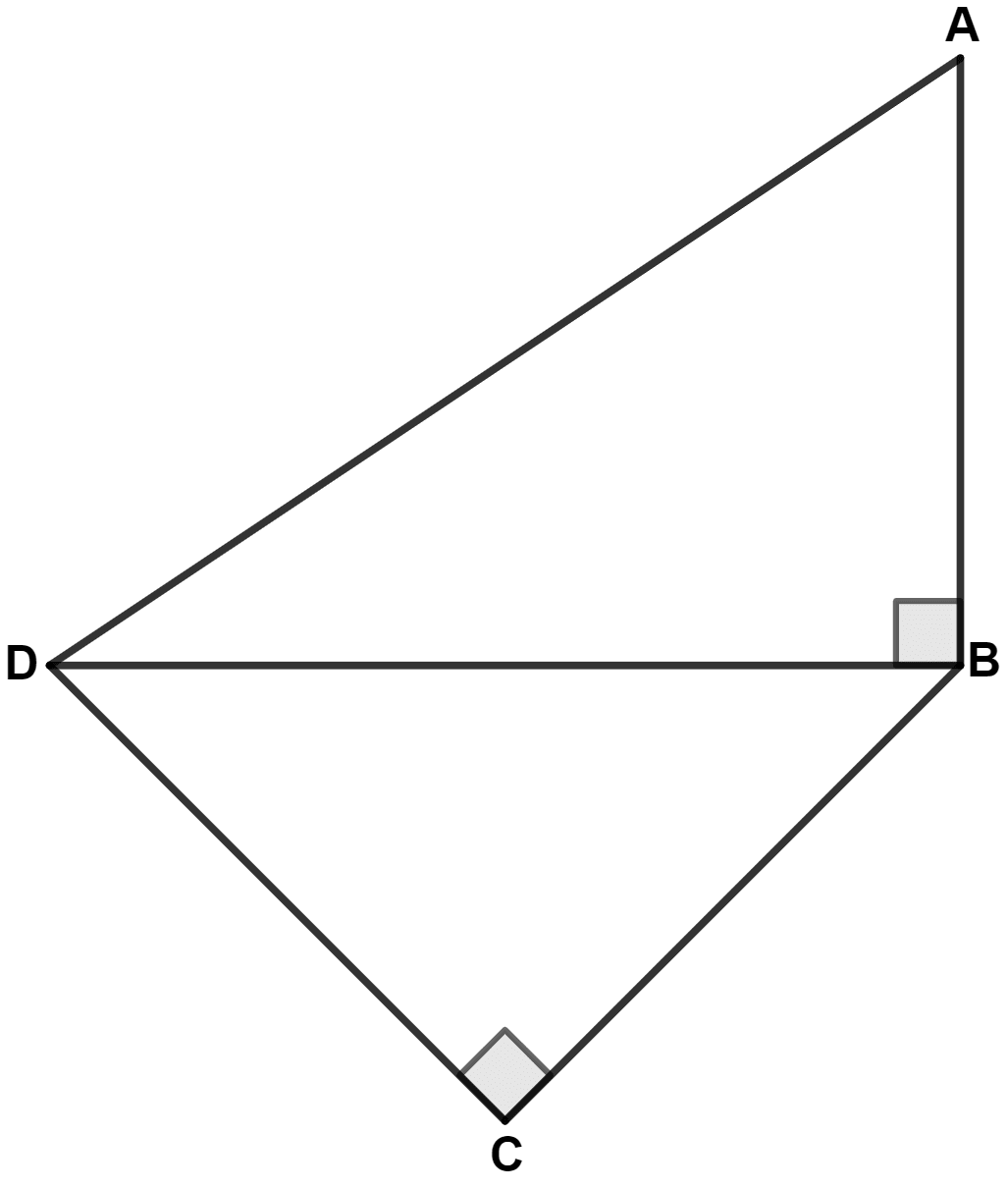
4 cm
3 cm
5 cm
6 cm