Mathematics
If the lengths of the sides of a triangle are in the ratio 5 : 12 : 13; then the triangle is :
acute-angled triangle
scalene triangle
scalene right-angled triangle
obtuse-angled triangle
Pythagoras Theorem
37 Likes
Answer
Given,
Lengths of the sides of a triangle are in the ratio 5 : 12 : 13.
Let length of the sides of triangle are 5x, 12x and 13x.
Squaring all the sides, we get :
⇒ (13x)2 = 169x2
⇒ (12x)2 = 144x2
⇒ (5x)2 = 25x2
⇒ (12x)2 + (5x)2 = 144x2 + 25x2 = 169x2.
Since,
⇒ (13x)2 = (12x)2 + (5x)2.
∴ Triangle obeys pythagoras theorem.
∴ Triangle is a scalene right-angled triangle.
Hence, Option 3 is the correct option.
Answered By
23 Likes
Related Questions
In a right-angled triangle, hypotenuse is 10 cm and the ratio of the other two sides is 3 : 4, the sides are :
6 cm and 4 cm
8 cm and 6 cm
3 cm and 4 cm
8 cm and 4 cm
ABC is an isosceles triangle with AB = AC = 12 cm and BC = 8 cm. The area of the triangle is :
cm2
cm2
cm2
cm2
In a rhombus, its diagonals are 30 cm and 40 cm, its perimeter is :
20 cm
10 cm
60 cm
100 cm
In the given figure, AD = 13 cm, DC = 12 cm and BC = 3 cm, then AB is equal to :
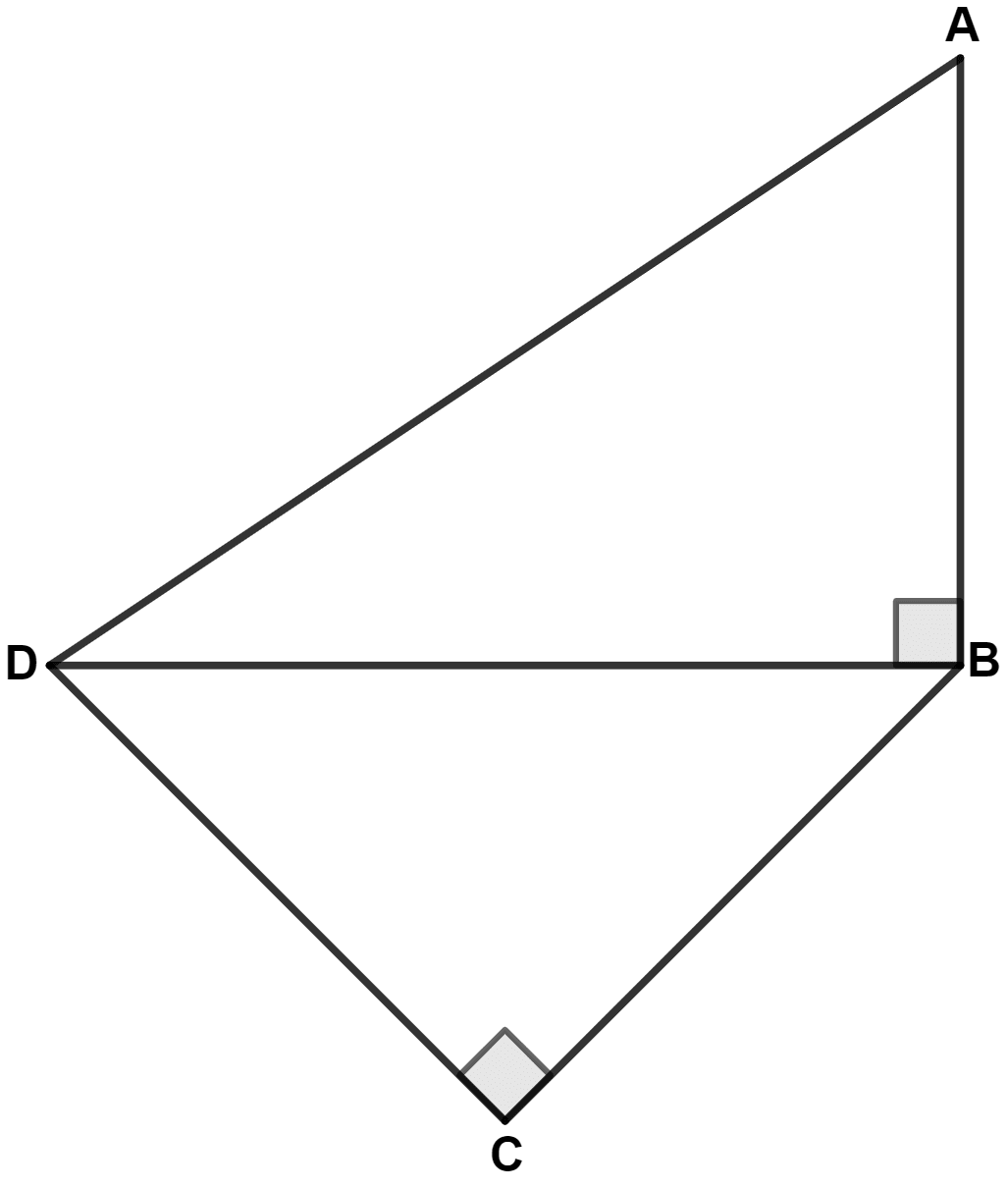
4 cm
3 cm
5 cm
6 cm