Mathematics
In a rhombus, its diagonals are 30 cm and 40 cm, its perimeter is :
20 cm
10 cm
60 cm
100 cm
Pythagoras Theorem
19 Likes
Answer
Let ABCD be the rhombus, with diagonals AC and BD intersecting at O.
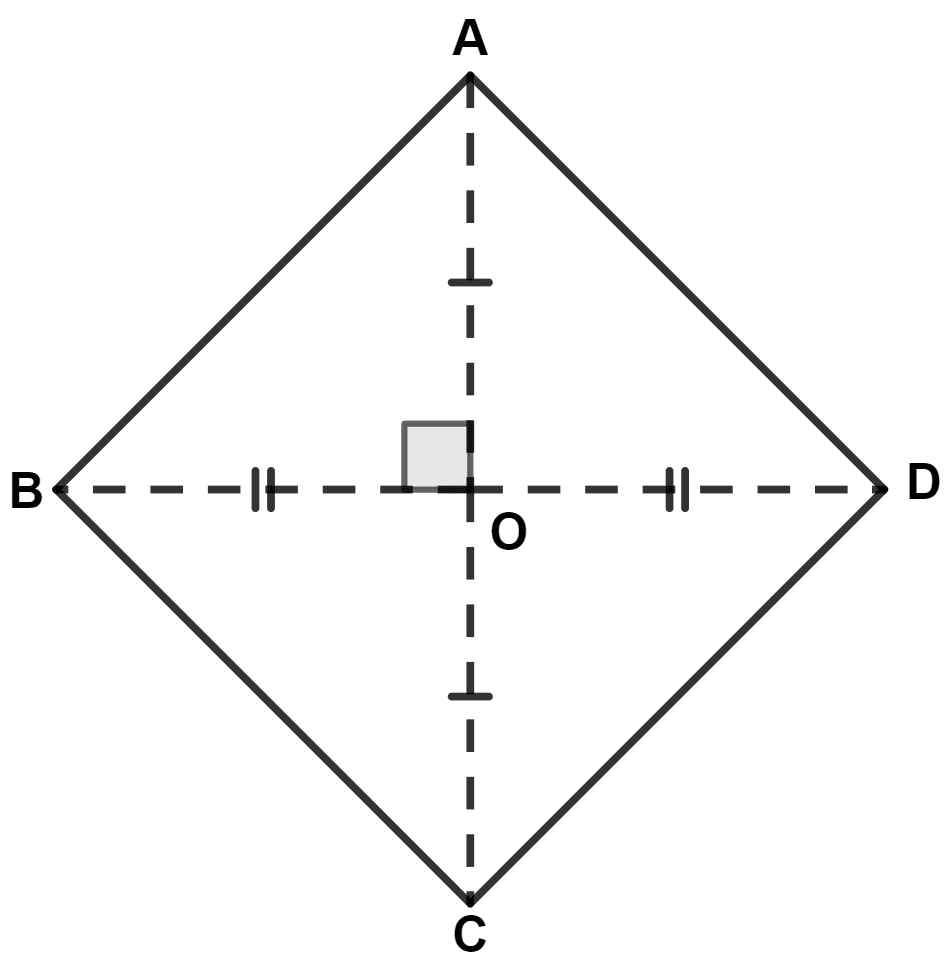
We know that,
Diagonals of rhombus intersect at right angles.
Let AC = 40 cm and BD = 30 cm.
∴ AO = = 15 cm.
In right angle triangle AOB,
By pythagoras theorem,
⇒ (Hypotenuse)2 = (Perpendicular)2 + (Base)2
⇒ AB2 = AO2 + BO2
⇒ AB2 = (20)2 + (15)2
⇒ AB2 = 400 + 225
⇒ AB2 = 625
⇒ AB = = 25 cm.
We know that,
All sides of rhombus are equal.
∴ Perimeter of rhombus = 4 × side = 4 × 25 = 100 cm.
Hence, Option 4 is the correct option.
Answered By
13 Likes
Related Questions
In a right-angled triangle, hypotenuse is 10 cm and the ratio of the other two sides is 3 : 4, the sides are :
6 cm and 4 cm
8 cm and 6 cm
3 cm and 4 cm
8 cm and 4 cm
ABC is an isosceles triangle with AB = AC = 12 cm and BC = 8 cm. The area of the triangle is :
cm2
cm2
cm2
cm2
In the given figure, AD = 13 cm, DC = 12 cm and BC = 3 cm, then AB is equal to :
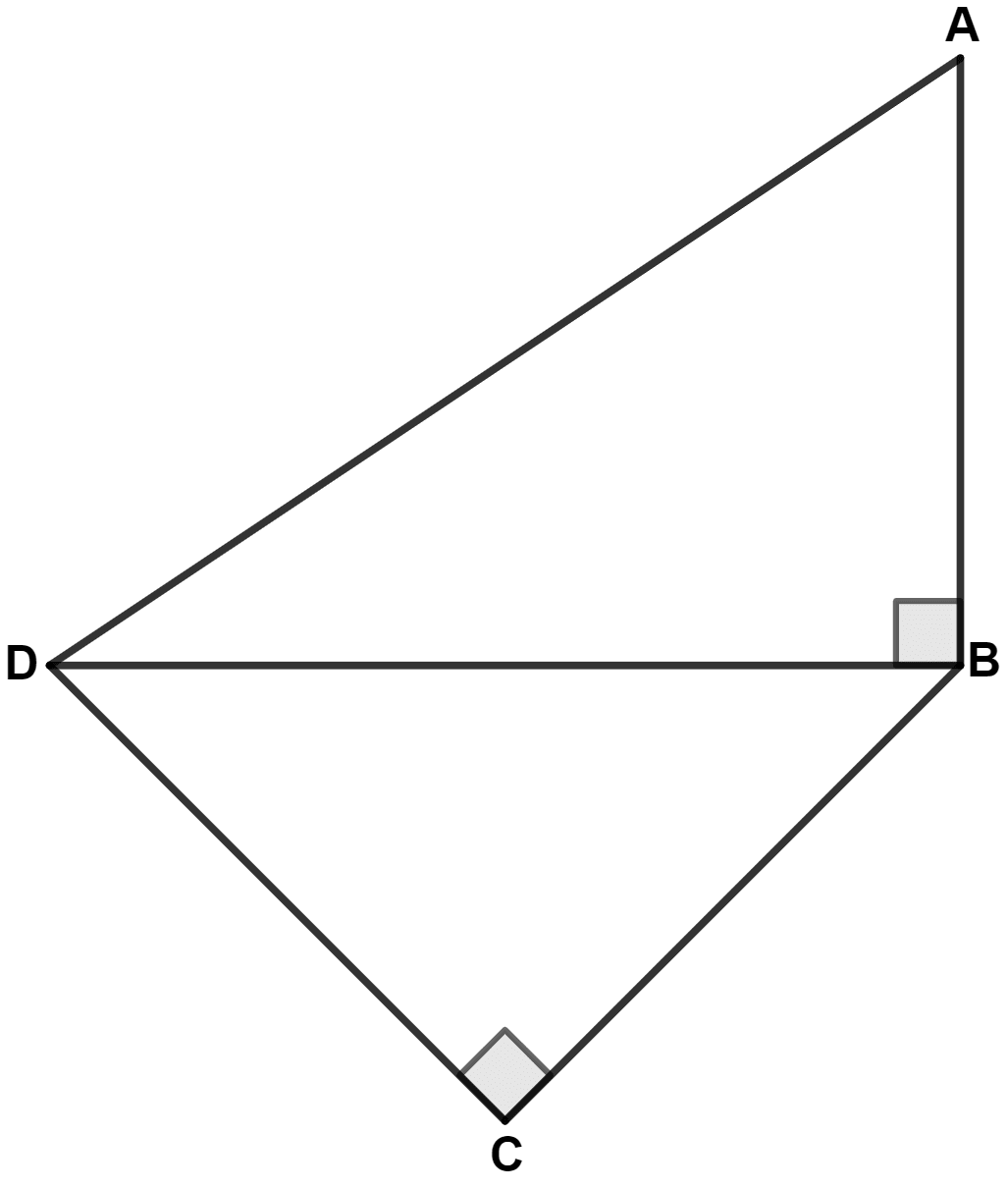
4 cm
3 cm
5 cm
6 cm
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.