Mathematics
ABCDE is a pentagon in which AB = AE, BC = ED and ∠ABC = ∠AED.
(a) Prove that :
(i) AC = AD
(ii) ∠BCD = ∠EDC
(b) If BC and ED are produced to meet at X, prove that BX = EX.
Rectilinear Figures
1 Like
Answer
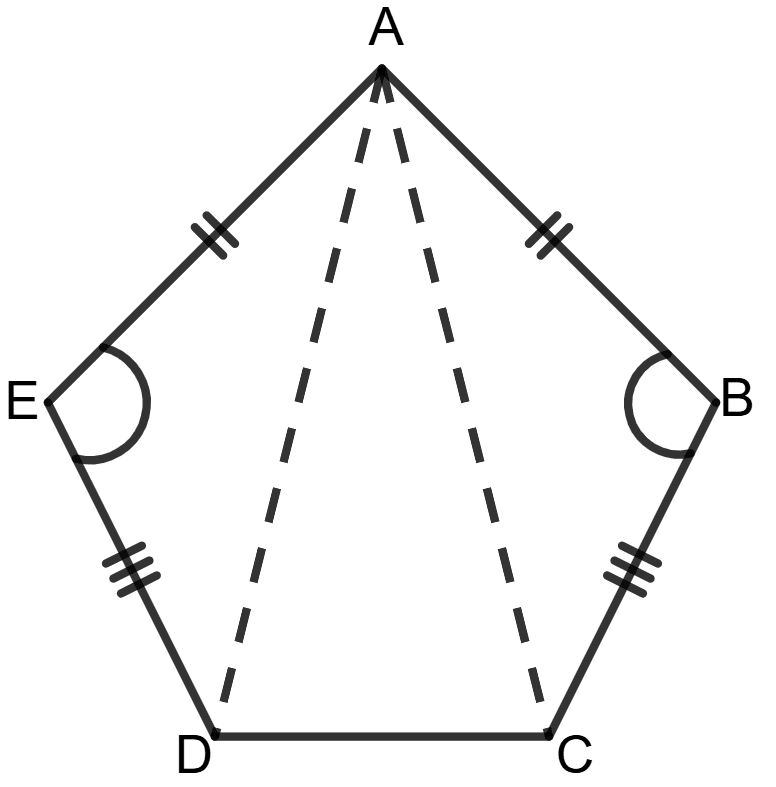
(a) Given: ABCDE is a pentagon in which AB = AE, BC = ED and ∠ABC = ∠AED.
To prove: (i) AC = AD
(ii) ∠BCD = ∠EDC
Proof: Consider Δ AED and Δ ABC,
AE = AB (Given)
ED = BC (Given)
∠AED = ∠ABC (Given)
Using SAS congruency criterion,
Δ AED ≅ Δ ABC
⇒ AD = AC (by C.P.C.T.)
Hence, AD = AC.
(ii) Since Δ AED ≅ Δ ABC (Proved above), we have:
⇒ ∠ADE = ∠ACB (by C.P.C.T.) ……………….(1)
Since AD = AC (proved above), Δ ACD is isosceles, so:
⇒ ∠ADC = ∠ACD ……………….(2)
Adding equations (1) and (2), we get:
⇒ ∠ADC + ∠ADE = ∠ACD + ∠ACB
⇒ ∠EDC = ∠BCD
Hence, ∠EDC = ∠BCD.
(b)
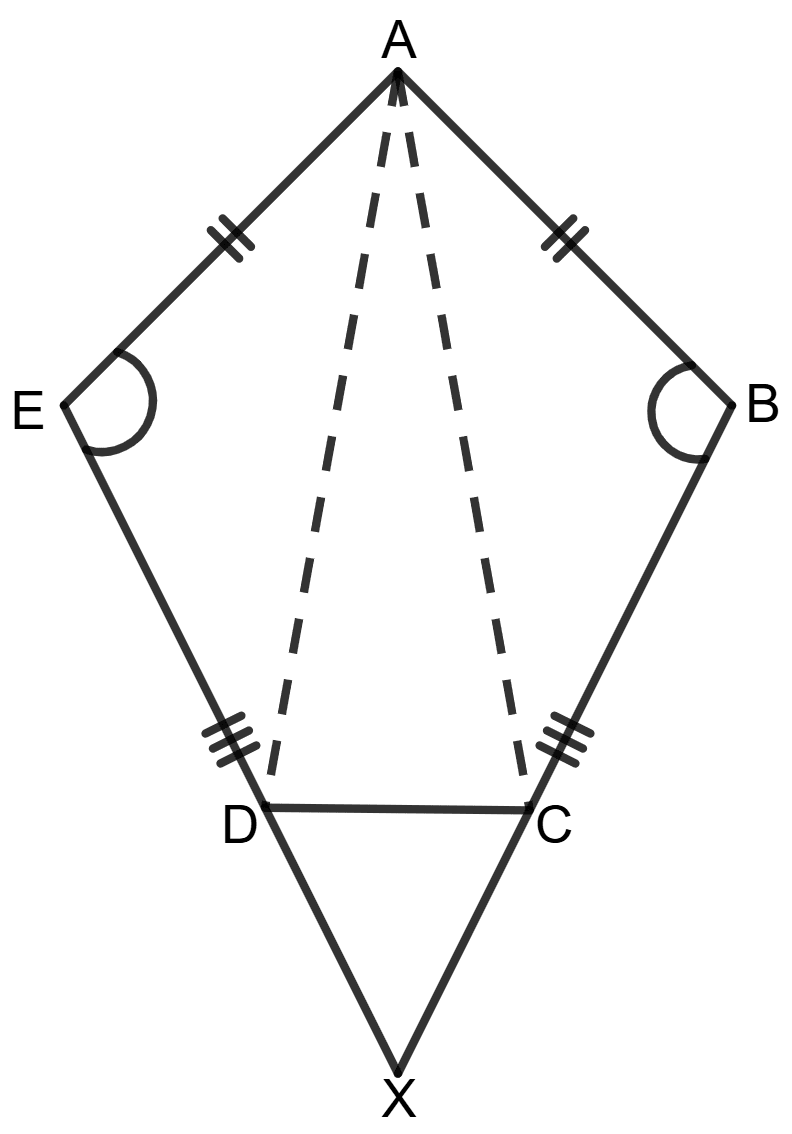
Since BC and ED are produced to meet at X, consider Δ XDC:
⇒ ∠XDC = 180° - ∠EDC
⇒ ∠XDC = 180° - ∠BCD (∠EDC = ∠BCD)
⇒ ∠XDC = ∠XCD
⇒ XC = XD ……………….(3)
As it is given , BC = DE ……………….(4)
Adding equations (3) and (4),
⇒ XC + BC = XD + DE
⇒ BX = EX
Hence, BX = EX.
Answered By
2 Likes
Related Questions
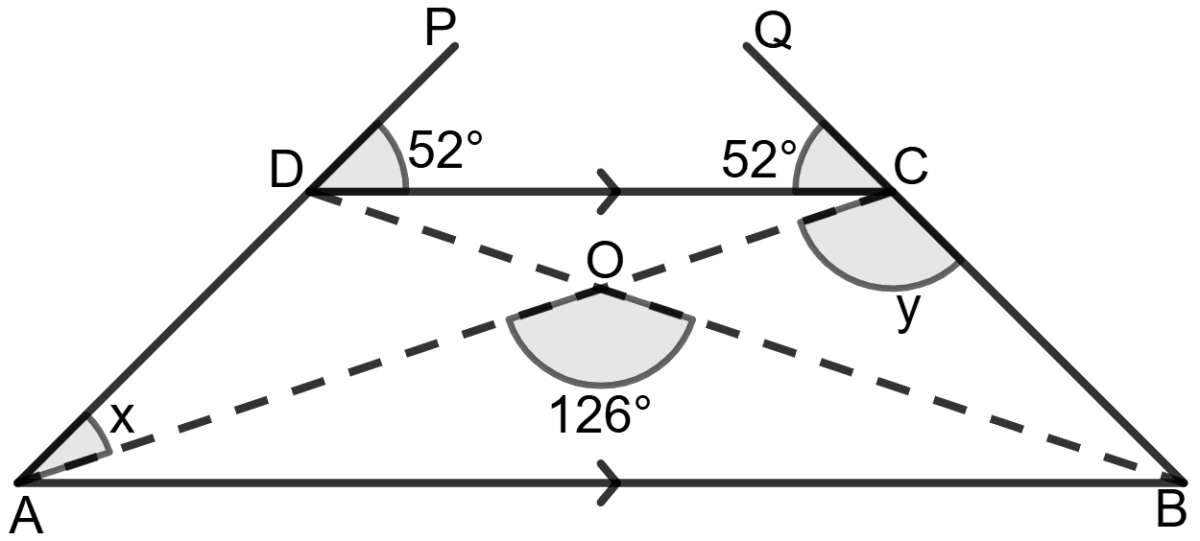
In the given figure, ABCD is a trapezium with DC//AB, ∠AOB = 126° and ∠DCQ = ∠CDP = 52°.
Find the values of x and y.
The perimeter of a parallelogram ABCD = 40 cm, AB = 3x cm, BC = 2x cm and CD = 2(y + 1) cm. Find the values of x and y.
In the parallelogram ABCD, M is mid-point of AC and X, Y are points on AB and DC respectively such that AX = CY.
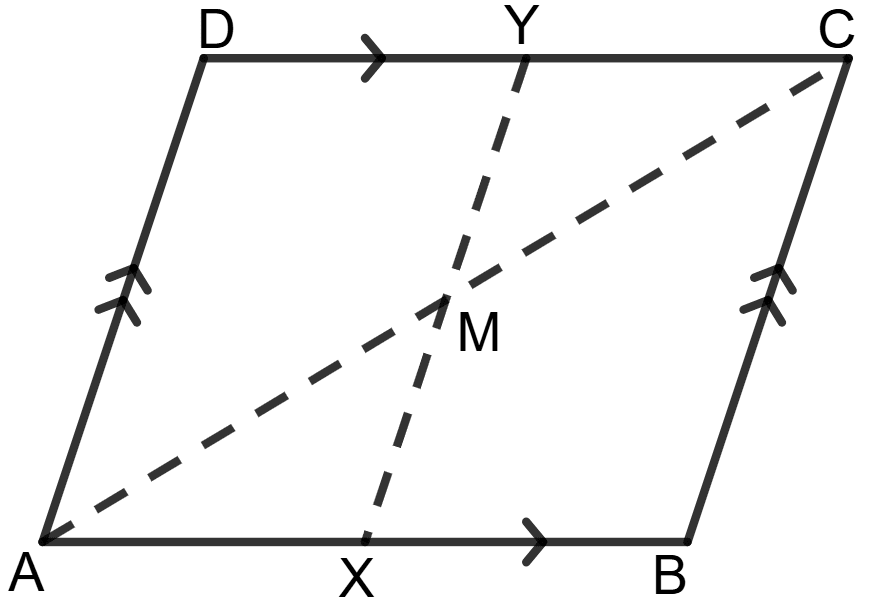
Prove that :
(i) triangle AXM is congruent to triangle CYM.
(ii) XMY is a straight line.
Construct a parallelogram in which diagonals are 6.5 cm and 4 cm long and angle between them is 60°.