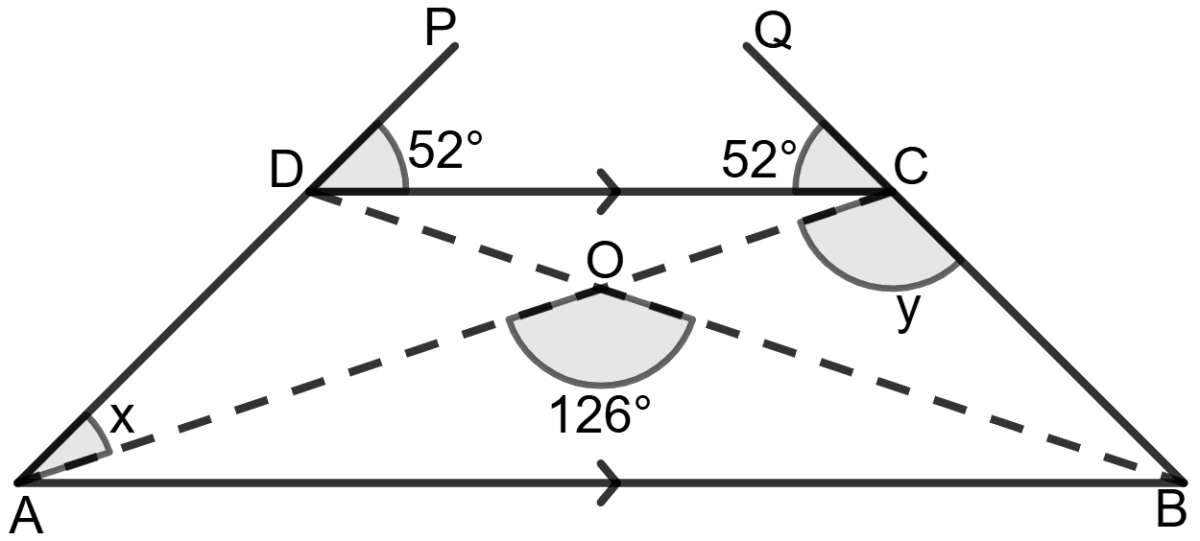
In the given figure, ABCD is a trapezium with DC//AB, ∠AOB = 126° and ∠DCQ = ∠CDP = 52°.

Find the values of x and y.

Given: ABCD is a trapezium with DC//AB, ∠AOB = 126° and ∠DCQ = ∠CDP = 52°.

To find: The values of x and y.

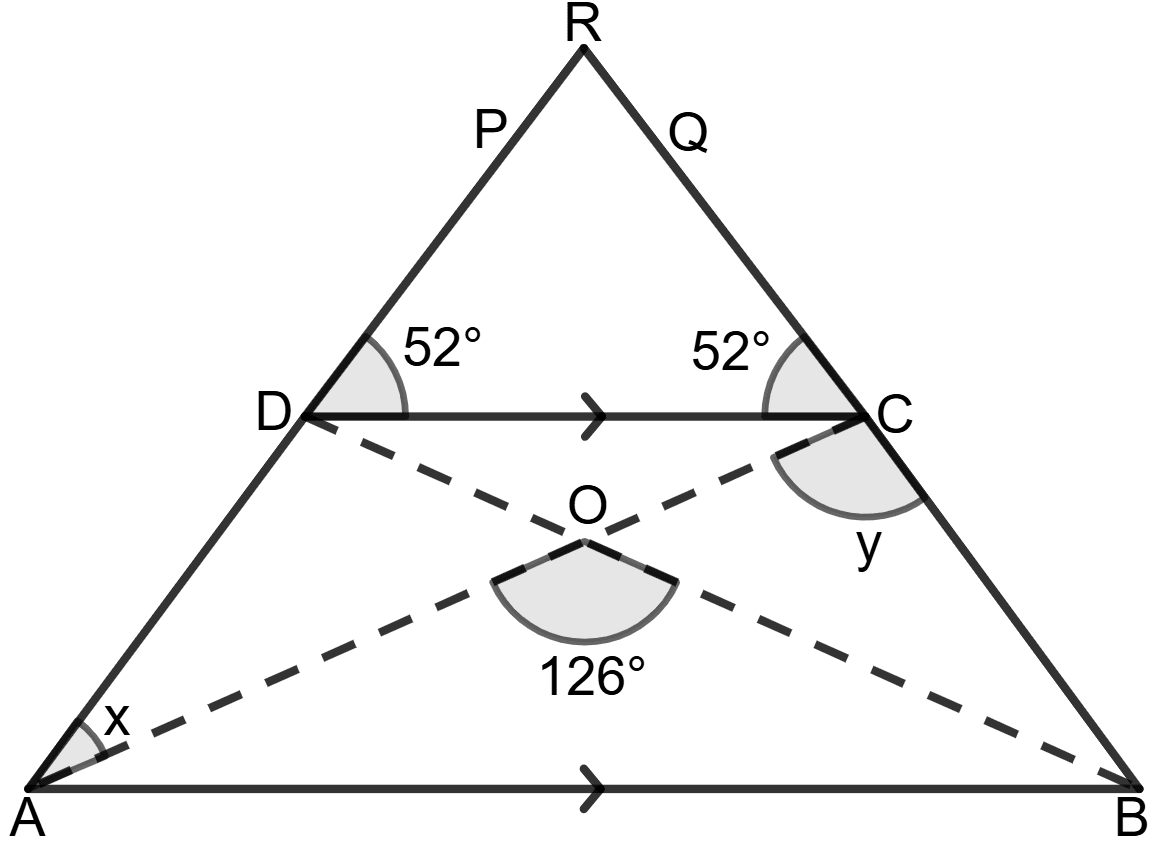
Construction: Extend P and Q such that they meet at R.

In Δ RDC,

⇒ ∠RDC = ∠RCD = 52° (since DCQ = CDP = 52°) ……………….(1)

Since the base angles are equal, Δ RDC is isosceles, which means:

⇒ DR = CR.

In quadrilateral ABCD, since AB ∥ DC, we use the property of corresponding angles:

⇒ ∠RAB = ∠RDC = 52° ( Corresponding angles) ………………..(2)

⇒ ∠RBA = ∠RCD = 52° ( Corresponding angles) ………………..(3)

Since ∠RAB = ∠RBA, we conclude that:

⇒ AR = RB

From the figure, we also note:

AD = AR - DR = RB - CR = BC

Therefore, we can say that ABCD is an isosceles trapezium.

Since, OA = OB, we conclude that:

⇒ ∠OAB = ∠OBA

Using the angle sum property in Δ AOB:

⇒ ∠OAB + ∠OBA + ∠AOB = 180°

⇒ ∠OAB + ∠OAB + 126° = 180°

⇒ 2∠OAB + 126° = 180°

⇒ 2∠OAB = 180° - 126°

⇒ 2∠OAB = 54°

⇒ ∠OAB = $\dfrac{54°}{2}$ = 27°

Now, ∠x = ∠DAB - ∠OAB = 52° - 27° = 25°

Using angle sum property in Δ ABC:

∠ABC + ∠BAC + ∠ACB = 180°

⇒ 52° + 27° + y = 180°

⇒ 79° + y = 180°

⇒ y = 180° - 79° = 101°

Hence, the value of x = 25° and y = 101°.