Mathematics
ABC is a triangle in which AB = AC and D is any point on BC. Prove that :
AB2 - AD2 = BD.CD
Pythagoras Theorem
6 Likes
Answer
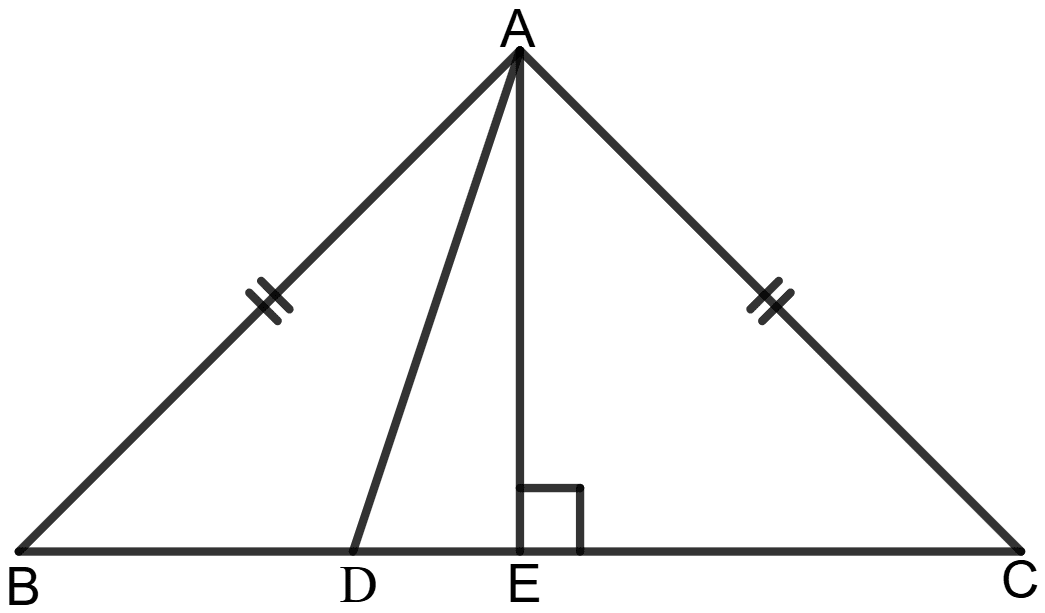
Given: ABC is a triangle in which AB = AC and D is any point on BC.
To prove: AB2 - AD2 = BD.CD
Construction: Draw AE ⊥ BC.
Proof: In Δ ABE and Δ ACE, we have:
AB = AC (Given)
AE = AE (Common)
∠AEB = ∠AEC (both are 90°)
Using RHS congruency criterion,
Δ ABE ≅ Δ ACE
⇒ BE = CE (by C.P.C.T.)
In Δ ABE, using Pythagorean theorem,
⇒ AB2 = AE2 + BE2 ……………….(1)
In Δ ADE, using Pythagorean theorem,
⇒ AD2 = AE2 + DE2 ……………….(2)
Subtracting equation (ii) from (i), we get:
⇒ AB2 - AD2 = (AE2 + BE2) - (AE2 + DE2)
⇒ AB2 - AD2 = AE2 + BE2 - AE2 - DE2
⇒ AB2 - AD2 = BE2 - DE2
⇒ AB2 - AD2 = (BE - DE)(BE + DE)
⇒ AB2 - AD2 = (BE - DE)(CE + DE) [∴ BE = CE]
⇒ AB2 - AD2 = BD.CD
Hence, AB2 - AD2 = BD.CD.
Answered By
3 Likes
Related Questions
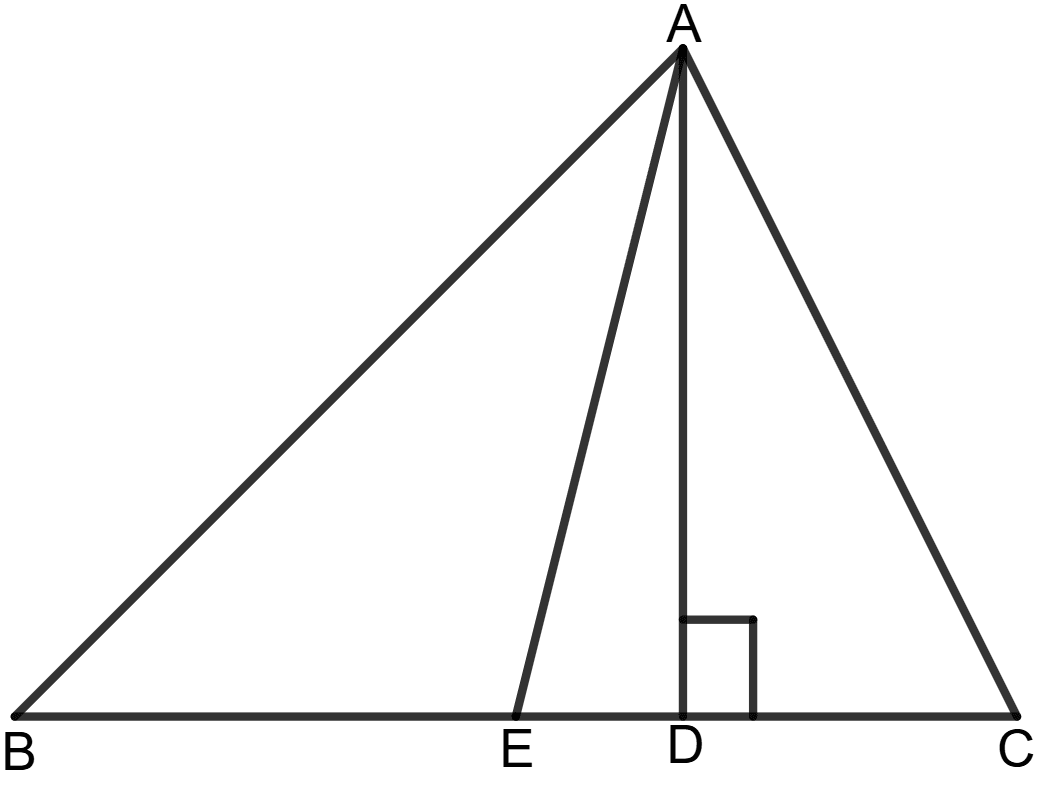
In triangle ABC, AB > AC. E is the mid-point of BC and AD is perpendicular to BC. Prove that :
AB2 + AC2 = 2AE2 + 2BE2
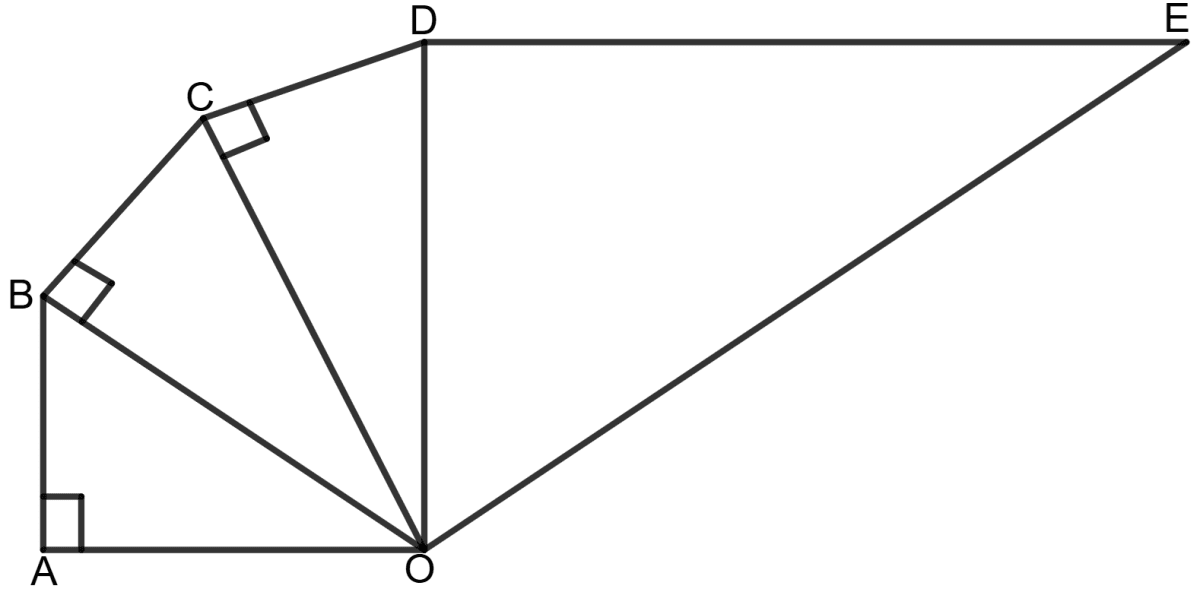
In the following figure :
OA = 2 cm = AB = 2BC = CD = DE
Find the length of OE.
ABC is an isosceles triangle with AB = AC = 2a and BC = a. If AD ⊥ BC, find the length of AD.
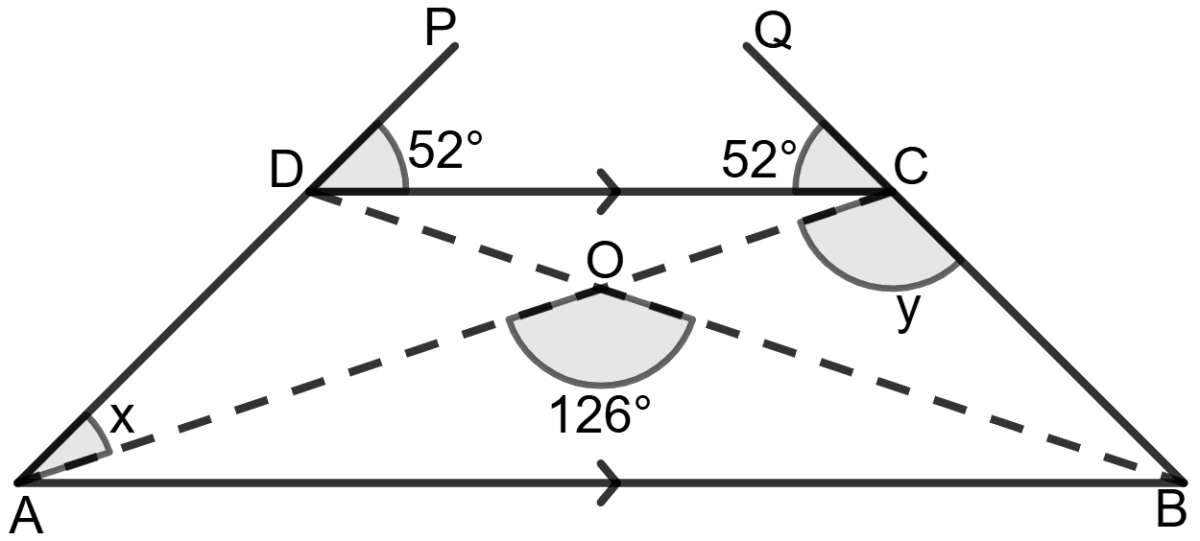
In the given figure, ABCD is a trapezium with DC//AB, ∠AOB = 126° and ∠DCQ = ∠CDP = 52°.
Find the values of x and y.