Mathematics
ABC is an isosceles triangle with AB = AC = 2a and BC = a. If AD ⊥ BC, find the length of AD.
Pythagoras Theorem
1 Like
Answer
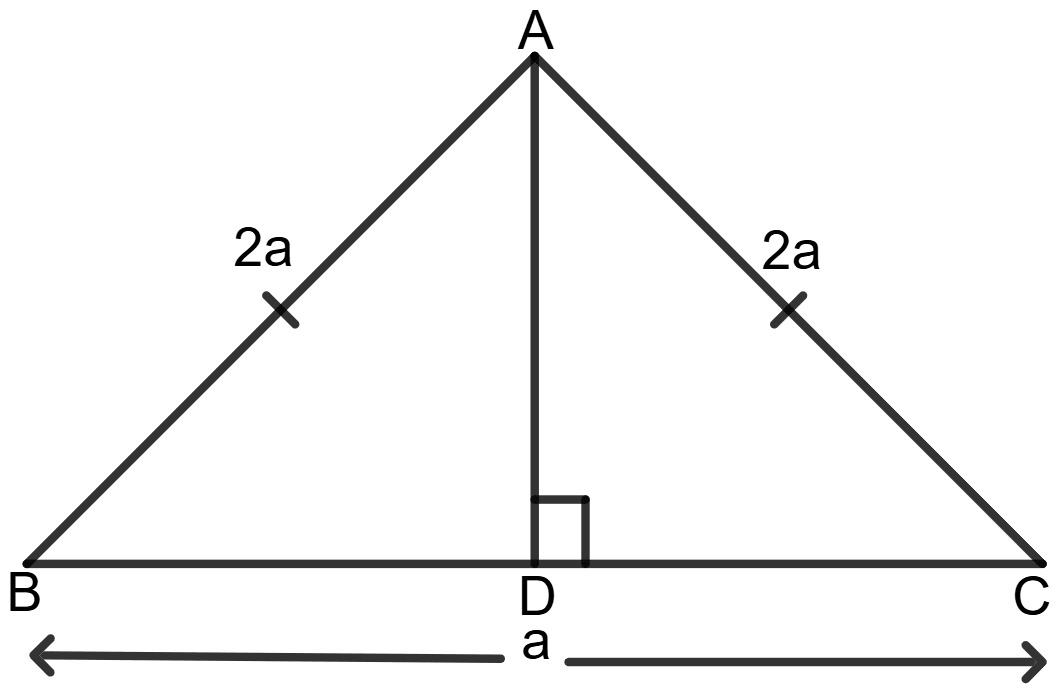
Given: AB = AC = 2a, BC = a and AD ⊥ BC.
Since Δ ABC is isosceles with AB = AC, the perpendicular from A to BC will bisects BC, meaning:
BD = DC =
In right-angled triangle ADB,
AB = 2a
BD =
Using the Pythagorean theorem,
AB2 = AD2 + BD2
⇒ (2a)2 = AD2 + 2
⇒ 4a2 = AD2 +
⇒ AD2 = 4a2 -
⇒ AD2 =
⇒ AD2 =
⇒ AD =
Hence, the length of the perpendicular from A to BC is units.
Answered By
2 Likes
Related Questions
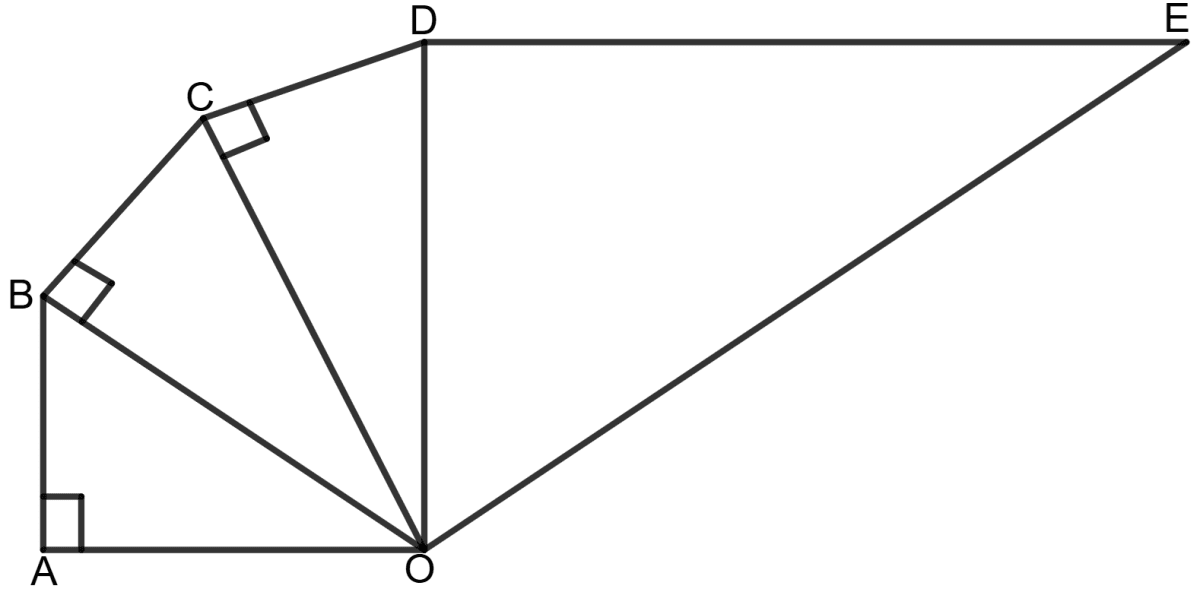
In the following figure :
OA = 2 cm = AB = 2BC = CD = DE
Find the length of OE.
ABC is a triangle in which AB = AC and D is any point on BC. Prove that :
AB2 - AD2 = BD.CD
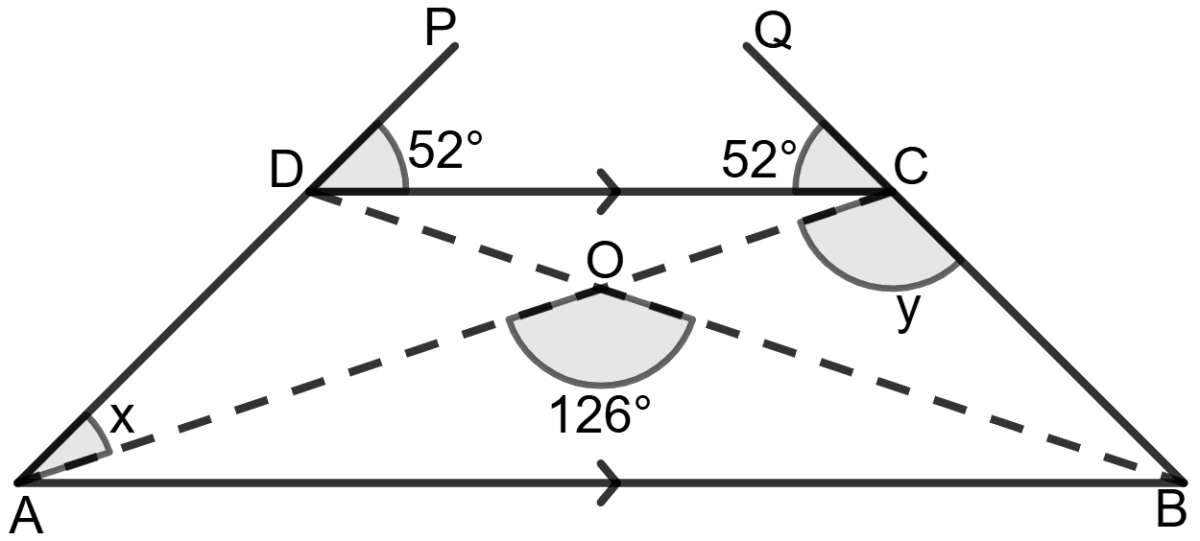
In the given figure, ABCD is a trapezium with DC//AB, ∠AOB = 126° and ∠DCQ = ∠CDP = 52°.
Find the values of x and y.
The perimeter of a parallelogram ABCD = 40 cm, AB = 3x cm, BC = 2x cm and CD = 2(y + 1) cm. Find the values of x and y.