Mathematics
Assertion (A): The median of : 25, 16, 26, 32, 31, 19, 28, 35 is 31.
Reason (R): To find median of the given data, the variate: x1, x2 , x3, ……………, xn needs to be arranged in ascending or descending order.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Statistics
4 Likes
Answer
A is false, R is true.
Explanation
On arranging the the given set of data in ascending order of magnitude, we get:
16, 19, 25, 26, 28, 31, 32, 35.
Number of observations, n = 8 (even)
Median =
=
=
=
=
=
= 27
∴ Assertion (A) is false.
To find median of the given data, the variate: x1, x2 , x3, ……………, xn needs to be arranged in ascending or descending order.
∴ Reason (R) is true.
Hence, Assertion (A) is false, Reason (R) is true.
Answered By
2 Likes
Related Questions
Assertion (A): The line segment joining the mid-points of all parallel chords of a circle passes through the centre.
Reason (R): If the chords are on same side of centre then only the line through the mid-points of the chords passes through the centre.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): In the given figure the lengths of arc AB and arc BC are in the ratio 2:1. If ∠AOB = 96°, then ∠AOC = 144°.
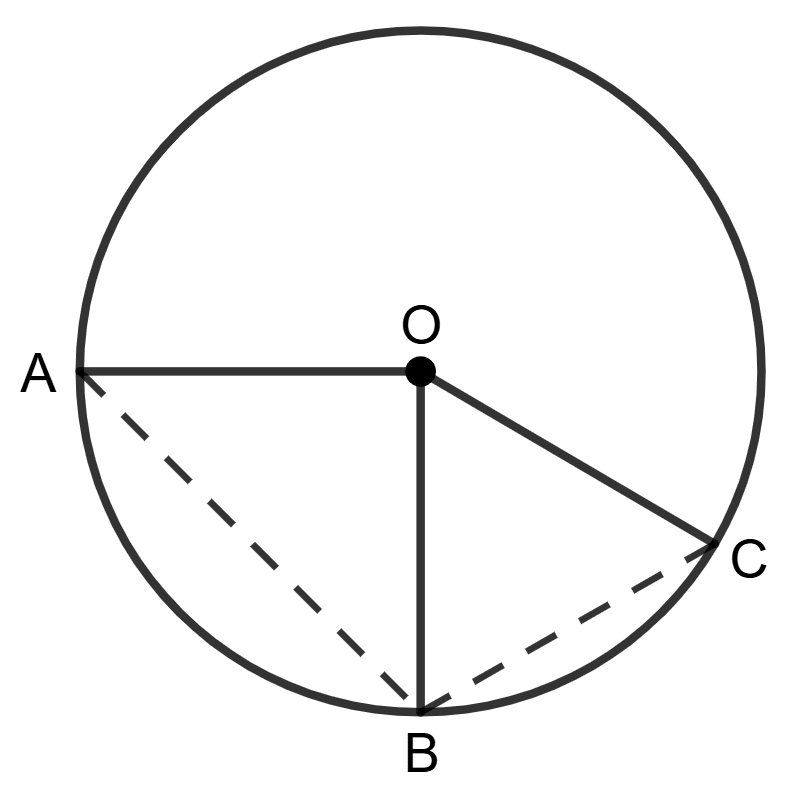
Reason (R): In two equal (congruent) circles if two arcs are equal, then they subtend equal angles at their centres.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): If the class marks of two overlapping intervals of equal size in a distribution are 94 and 104 then the corresponding intervals are 89-99, 99-109.
Reason (R): The class mark of a class interval
=
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): In a frequency distribution the class marks are 5, 15 and 25. The corresponding class-intervals are 5 - 15 and 15 - 25.
Reason (R): ∵ and
∴ Class-intervals are : (5 - 5) - (5 + 5), (15 - 5) - (15 + 5) and (25 - 5) - (25 + 5)- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.