Mathematics
If a, c, a2 + b2 and b2 + c2 are in proportion, show that b is mean proportion between a and c.
Ratio Proportion
15 Likes
Answer
Given,
a, c, a2 + b2 and b2 + c2 are in proportion.
Hence, proved that b is the mean proportion between a and c.
Answered By
6 Likes
Related Questions
Geeta needs ₹ 31,800 at the end of 2 years from now. How much money, should she deposit in a recurring deposit account to get the required amount ? The rate of interest is 10%.
(i) Express in terms of sec A and tan A.
(ii) Express in terms of sec A and tan A.
(iii) Prove that : = 2 tan A
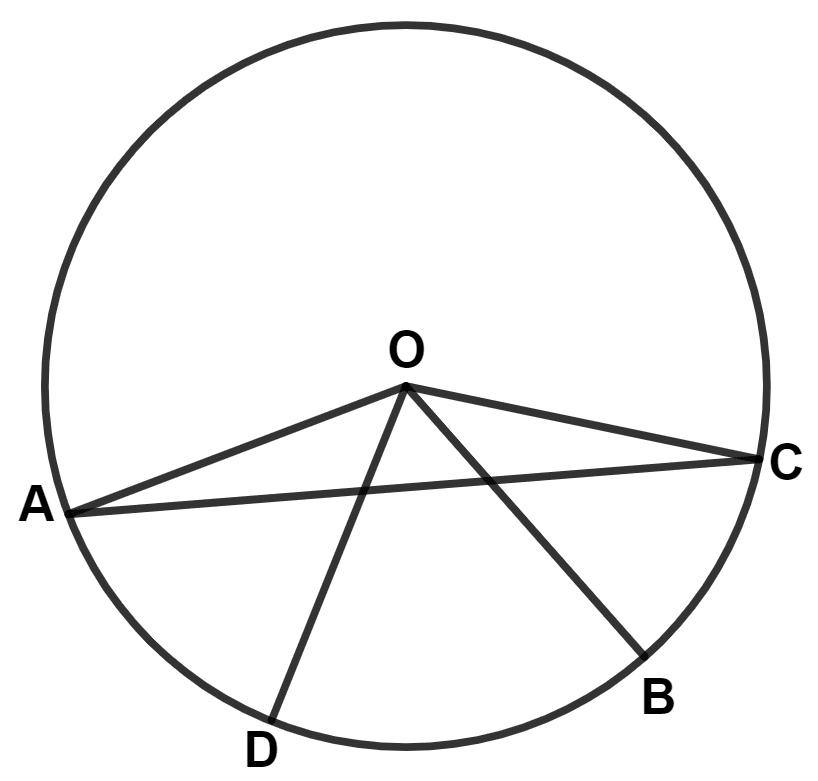
The given figure shows a circle with center O. Points A, D, B and C lie on the circumference of the given circle and angle AOB = 108°. If arc ADB = 2 × arc BC, find :
(i) ∠ACB
(ii) ∠CAB
(iii) ∠ADB
The daily wages of 160 workers in a building project are given below :
Wages (in ₹) No. of workers 130-140 48 140-150 34 150-160 26 160-170 32 170-180 20 Draw a cumulative frequency curve and use it to estimate :
(i) the median wage
(ii) semi-inter quartile range
(iii) percentage of workers who earn between ₹ 145 and ₹ 165.