Mathematics
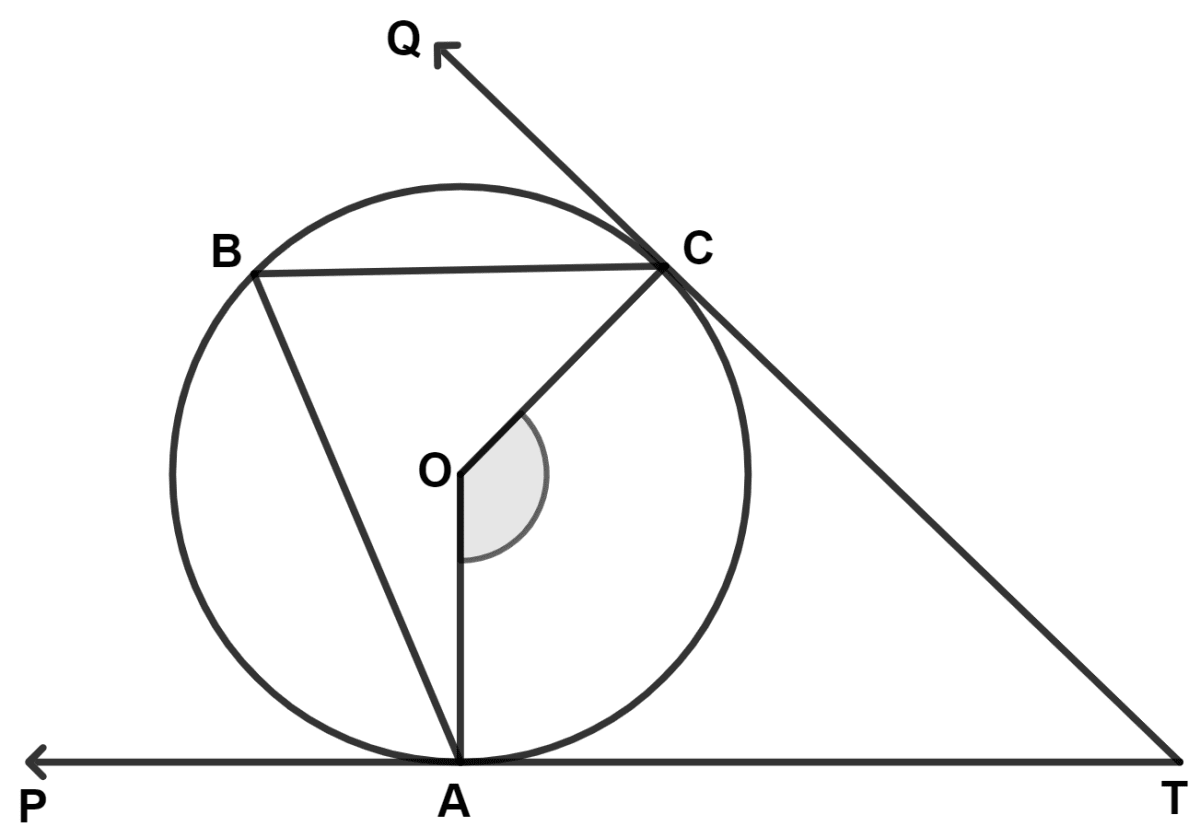
In the given figure, TP and TQ are two tangents to the circle with center O, touching the circle at points A and C respectively. If ∠BCQ = 55°, ∠BAP = 60°, find :
(i) ∠OBA
(ii) ∠OBC
(iii) ∠AOC
(iv) ∠ATC
Circles
61 Likes
Answer
(i) ∠OAP = 90° [As TP is tangent at point A]
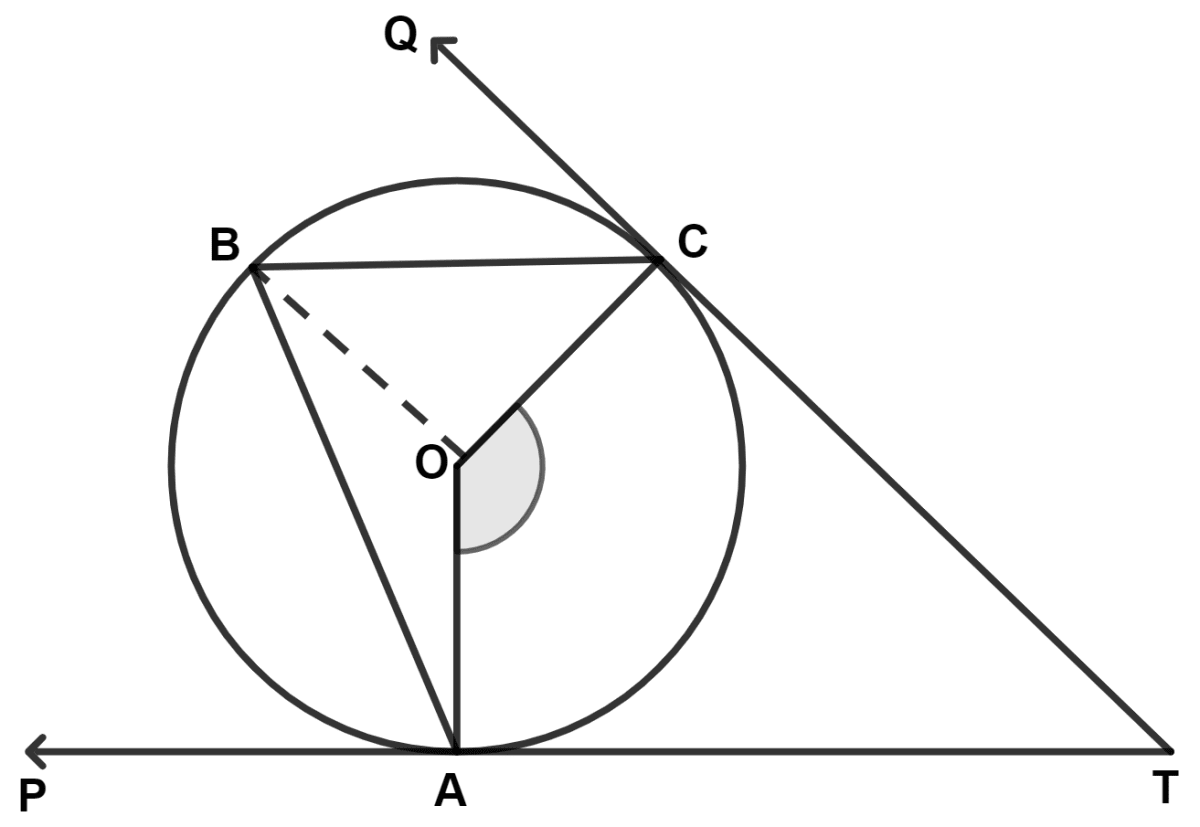
From figure,
⇒ ∠OAB = ∠OAP - ∠BAP = 90° - 60° = 30°.
⇒ OA = OB (Radius of same circle)
⇒ ∠OBA = ∠OAB = 30° (Angles opposite to equal sides are equal)
Hence, ∠OBA = 30°.
(ii) ∠OCQ = 90° [As TQ is tangent at point C]
From figure,
∠OCB = ∠OCQ - ∠BCQ = 90° - 55° = 35°.
⇒ OB = OC (Radius of same circle)
⇒ ∠OBC = ∠OCB = 35° (Angles opposite to equal sides are equal)
Hence, ∠OBC = 35°.
(iii) We know that,
The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
⇒ ∠AOC = 2∠ABC
⇒ ∠AOC = 2(∠OBA + ∠OBC)
⇒ ∠AOC = 2(30° + 35°)
⇒ ∠AOC = 2 × 65° = 130°.
Hence, ∠AOC = 130°.
(iv) In quadrilateral OATC,
⇒ ∠AOC + ∠OAT + ∠OCT + ∠ATC = 360°
⇒ 130° + 90° + 90° + ∠ATC = 360°
⇒ 310° + ∠ATC = 360°
⇒ ∠ATC = 360° - 310° = 50°.
Hence, ∠ATC = 50°.
Answered By
39 Likes
Related Questions
The mean of the following distribution is 50 and the frequency of the class-interval 20-40 is m, find the value of m.
Class-interval Frequency 0-20 17 20-40 m 40-60 32 60-80 24 80-100 19 The following table shows the marked price, the discount, the number of items and GST rates for two items A and B.
Items Marked price Discount No. of items GST A ₹ 1000 10% 2 0% B ₹ 2000 20% 1 5% Find the total of the money for the above statement.
If the third, sixth and the last terms of a G.P. are 6, 48 and 3072 respectively, find the first term and the numbers of terms in the G.P.
Find the mode of the following distribution by drawing a histogram :
Mid-value Frequency 28 10 34 8 40 24 46 16 52 8