In square PQRS :

(i) if PQ = 3x - 7 and QR = x + 3, find PS.

(ii) if PR = 5x and QS = 9x — 8. Find QS.

(i) In a square PQRS, all sides are equal and all angles are 90°.

Thus, PQ = QR = PS = RS.

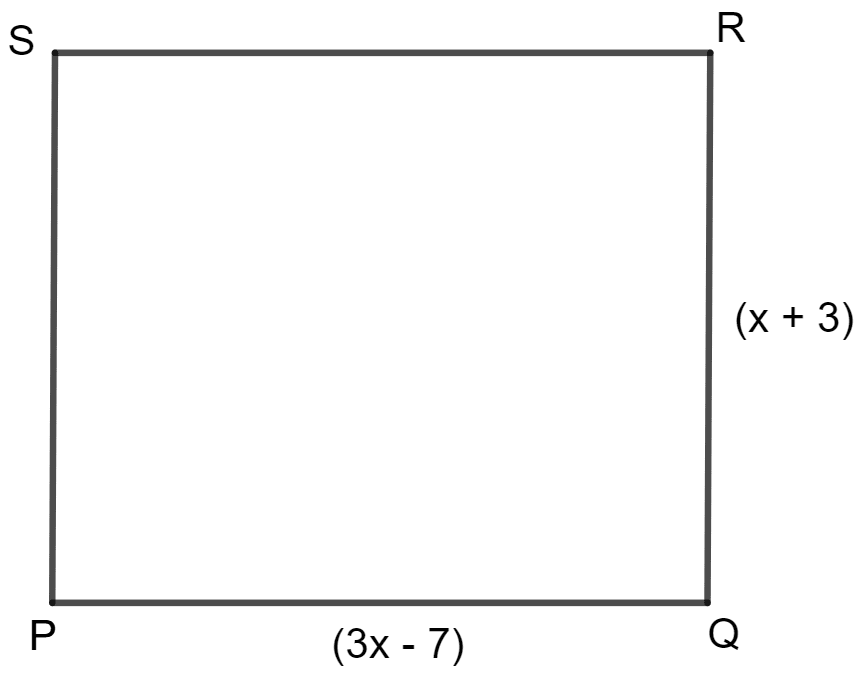
It is given that PQ = 3x - 7 and QR = x + 3.

⇒ (3x - 7) = (x + 3)

⇒ 3x - 7 = x + 3

⇒ 3x - x = 7 + 3

⇒ 2x = 10

⇒ x = $\dfrac{10}{2}$

⇒ x = 5

Now, substitute the value of x = 5 into the expression for PQ:

PQ = QR = PS = RS = (3x - 7)

= (3 $\times$ 5 - 7)

= (15 - 7)

= 8

Hence, the length of PS = 8 units.

(ii) In a square PQRS, all sides are equal and all angles are 90°.

Thus, PQ = QR = PS = RS.

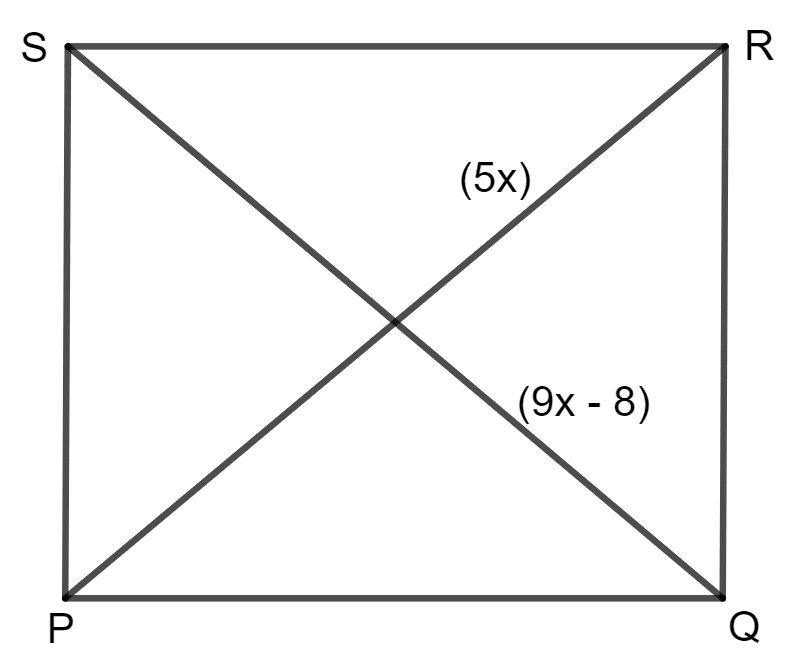
It is given that PR = 5x and QS = 9x - 8.

⇒ (5x) = (9x - 8)

⇒ 5x = 9x - 8

⇒ 9x - 5x = 8

⇒ 4x = 8

⇒ x = $\dfrac{8}{4}$

⇒ x = 2

Now, substitute the value of x = 2 into the expression for PQ:

PQ = QR = PS = RS = 5x

= 5 $\times$ 2

= 10

Hence, the length of QS = 10 units.