Mathematics
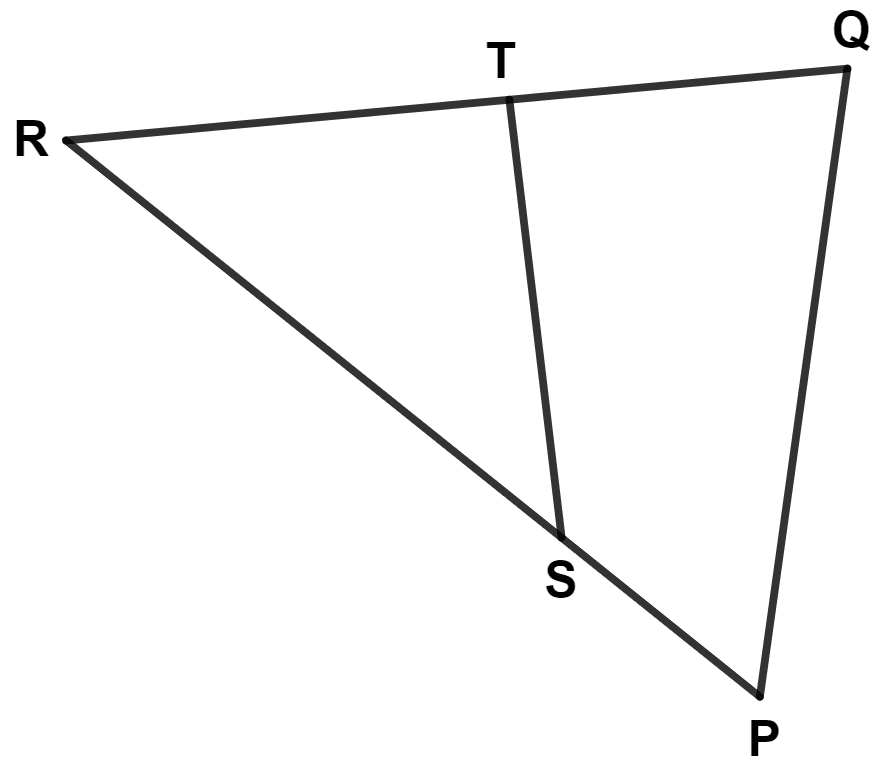
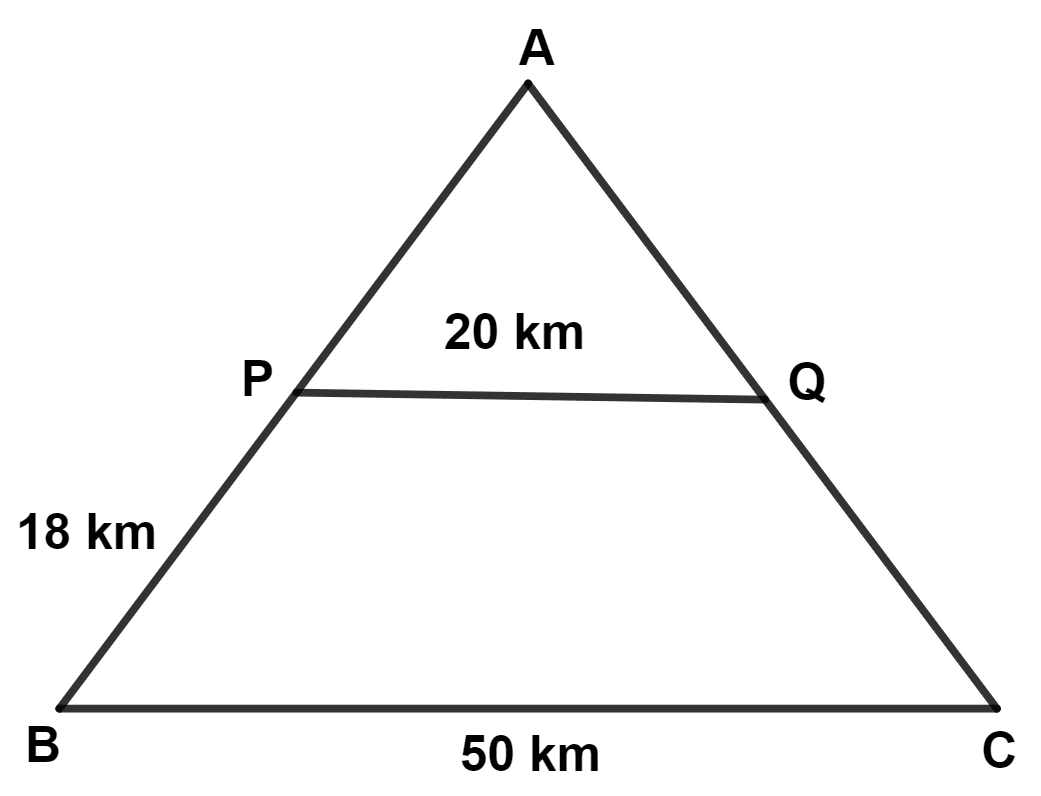
In the given diagram (not draw to scale), railway stations A, B, C, P and Q are connected by straight tracks. Track PQ is parallel to BC. The time taken by a train travelling at 90 km/hr to reach B from A by the shortest route is :
8 minutes
12 minutes
16.8 minutes
20 minutes
Similarity
51 Likes
Answer
In △ APQ and △ ABC,
⇒ ∠PAQ = ∠BAC (Common angle)
⇒ ∠APQ = ∠ABC (Corresponding angles are equal)
∴ △ APQ ~ △ ABC (By A.A. axiom)
From figure,
Let AP = x km.
We know that,
Corresponding sides of similar triangle are proportional.
AB = AP + BP = 12 + 18 = 30 km.
Time = = 20 minutes.
Hence, Option 4 is the correct option.
Answered By
27 Likes
Related Questions
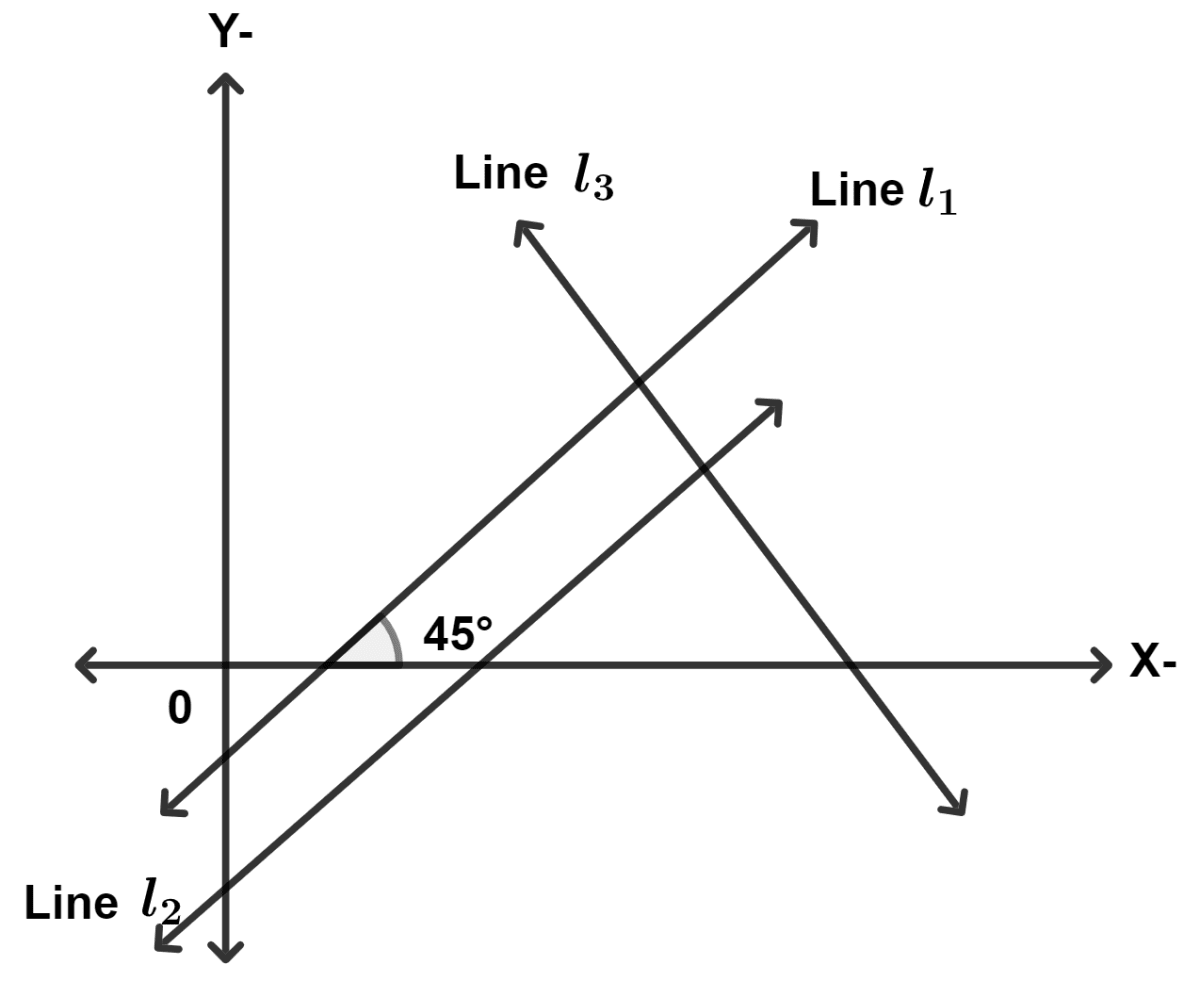
In the given figure line l1 is a parallel to line l2. If line l3 is perpendicular to line l1, then the slopes of lines l2 and l3 respectively are :
1, 1
-1, -1
1, -1
-1, 1
Which of the following lines cut the positive x-axis and positive y-axis at equal distances form the origin?
3x + 3y = 6
5x + 10y = 10
-x + y = 1
10x + 5y = 5
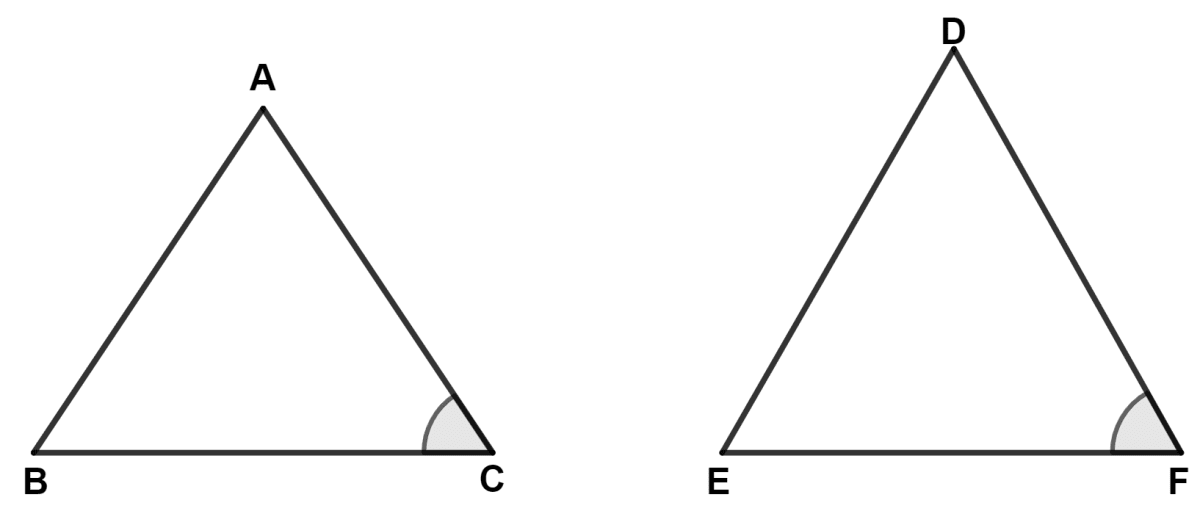
In the given diagram, △ ABC and △ DEF (not drawn to scale) are such that ∠C = ∠F and , then
△ ABC ~ △ DEF
△ BCA ~ △ DEF
△ CAB ~ △ DEF
the similarity of given triangles cannot be determined.
In the adjoining diagram, ST is not parallel to PQ. The necessary and sufficient conditions for △ PQR ~ △ TSR is :
∠PQR = ∠STR
∠QPR = ∠TSR
∠PQR = ∠TSR
∠PRQ = ∠RST