Mathematics
The perimeter of a parallelogram ABCD = 40 cm, AB = 3x cm, BC = 2x cm and CD = 2(y + 1) cm. Find the values of x and y.
Rectilinear Figures
2 Likes
Answer
The perimeter of a parallelogram ABCD = 40 cm.
AB = 3x cm, BC = 2x cm and CD = 2(y + 1) cm.
In a parallelogram, opposite sides are equal:
AB = CD and BC = DA
The perimeter of a parallelogram is given by:
⇒ Perimeter = AB + BC + CD + DA
⇒ 40 = AB + BC + AB + BC
⇒ 40 = 3x + 2x + 3x + 2x
⇒ 40 = 10x
⇒ x = = 4 cm
Since CD = AB,
⇒ 2(y + 1) = 3x
⇒ 2y + 2 = 3 x 4
⇒ 2y + 2 = 12
⇒ 2y = 12 - 2
⇒ 2y = 10
⇒ y = = 5
Hence, the values are x = 4 cm and y = 5 cm.
Answered By
1 Like
Related Questions
ABC is an isosceles triangle with AB = AC = 2a and BC = a. If AD ⊥ BC, find the length of AD.
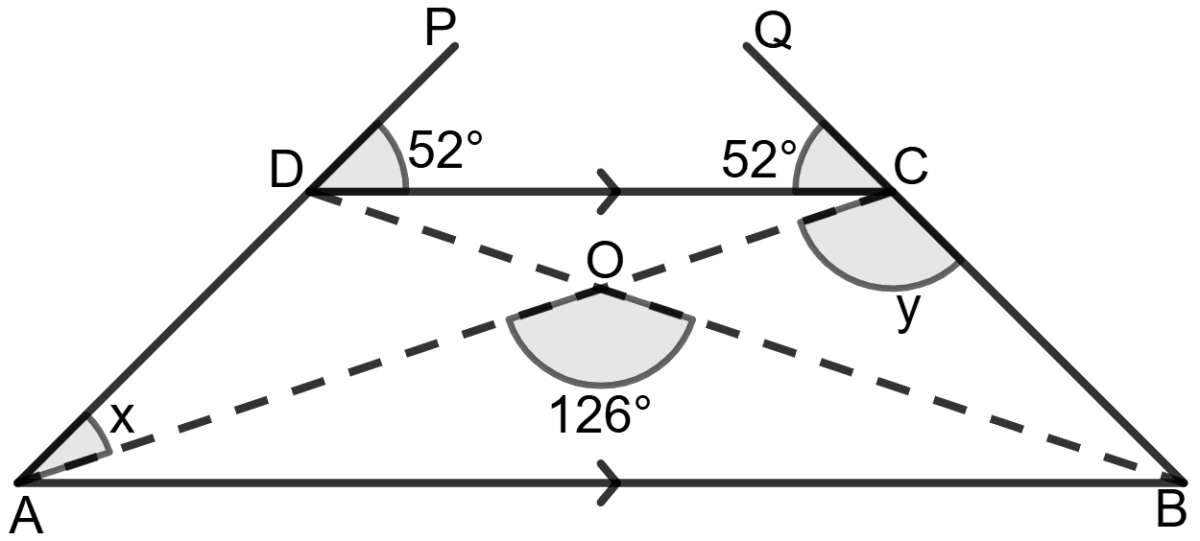
In the given figure, ABCD is a trapezium with DC//AB, ∠AOB = 126° and ∠DCQ = ∠CDP = 52°.
Find the values of x and y.
ABCDE is a pentagon in which AB = AE, BC = ED and ∠ABC = ∠AED.
(a) Prove that :
(i) AC = AD
(ii) ∠BCD = ∠EDC
(b) If BC and ED are produced to meet at X, prove that BX = EX.
In the parallelogram ABCD, M is mid-point of AC and X, Y are points on AB and DC respectively such that AX = CY.
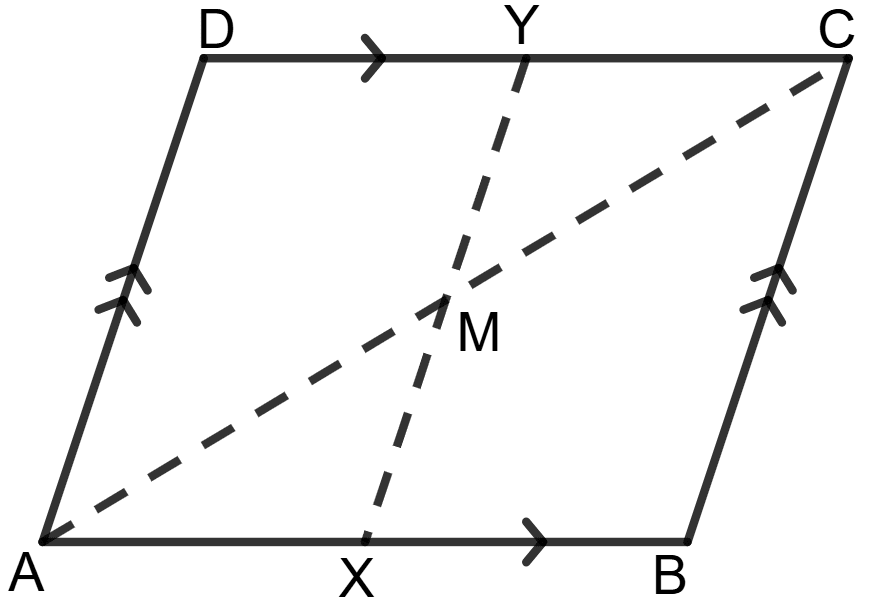
Prove that :
(i) triangle AXM is congruent to triangle CYM.
(ii) XMY is a straight line.