Mathematics
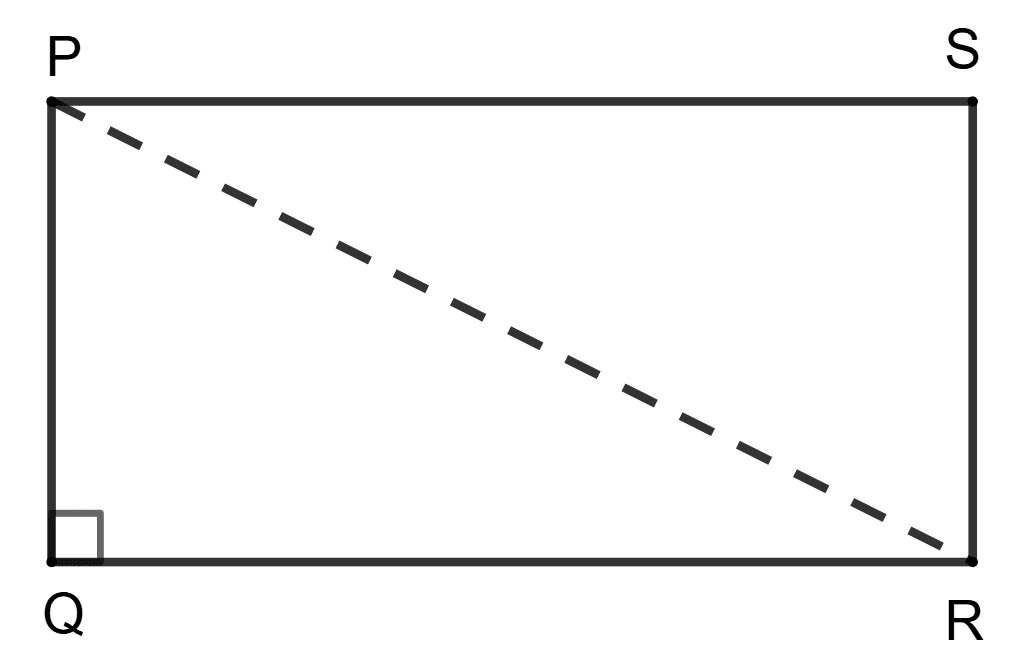
In a quadrilateral PQRS, ∠Q = ∠S = 90° then prove that 2PR2 - QR2 = PQ2 + PS2 + SR2.
Pythagoras Theorem
61 Likes
Answer
In quadrilateral PQRS, since ∠Q = ∠S = 90°, triangles PQR and PSR are right-angled triangles.
According to Pythagoras theorem,
In a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
⇒ Hypotenuse2 = Base2 + Height2
In triangle PQR,
⇒ PR2 = PQ2 + QR2 ………………….(1)
In triangle PSR,
⇒ PR2 = PS2 + SR2 ………………(2)
Adding eq (1) and (2):
⇒ PR2 + PR2 = PQ2 + QR2 + PS2 + SR2
⇒ 2PR2 = PQ2 + PS2 + SR2 + QR2
⇒ 2PR2 - QR2 = PQ2 + PS2 + SR2
Hence, proved that 2PR2 - QR2 = PQ2 + PS2 + SR2.
Answered By
39 Likes
Related Questions
A man goes 40 m due north and then 50 m due west. Find his distance from the starting point.
In the figure : ∠PSQ = 90°, PQ = 10 cm, QS = 6 cm and RQ = 9 cm. Calculate the length of PR.
AD is drawn perpendicular to base BC of an equilateral triangle ABC. Given BC = 10 cm, find the length of AD, correct to 1 place of decimal.
In triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC.