Mathematics
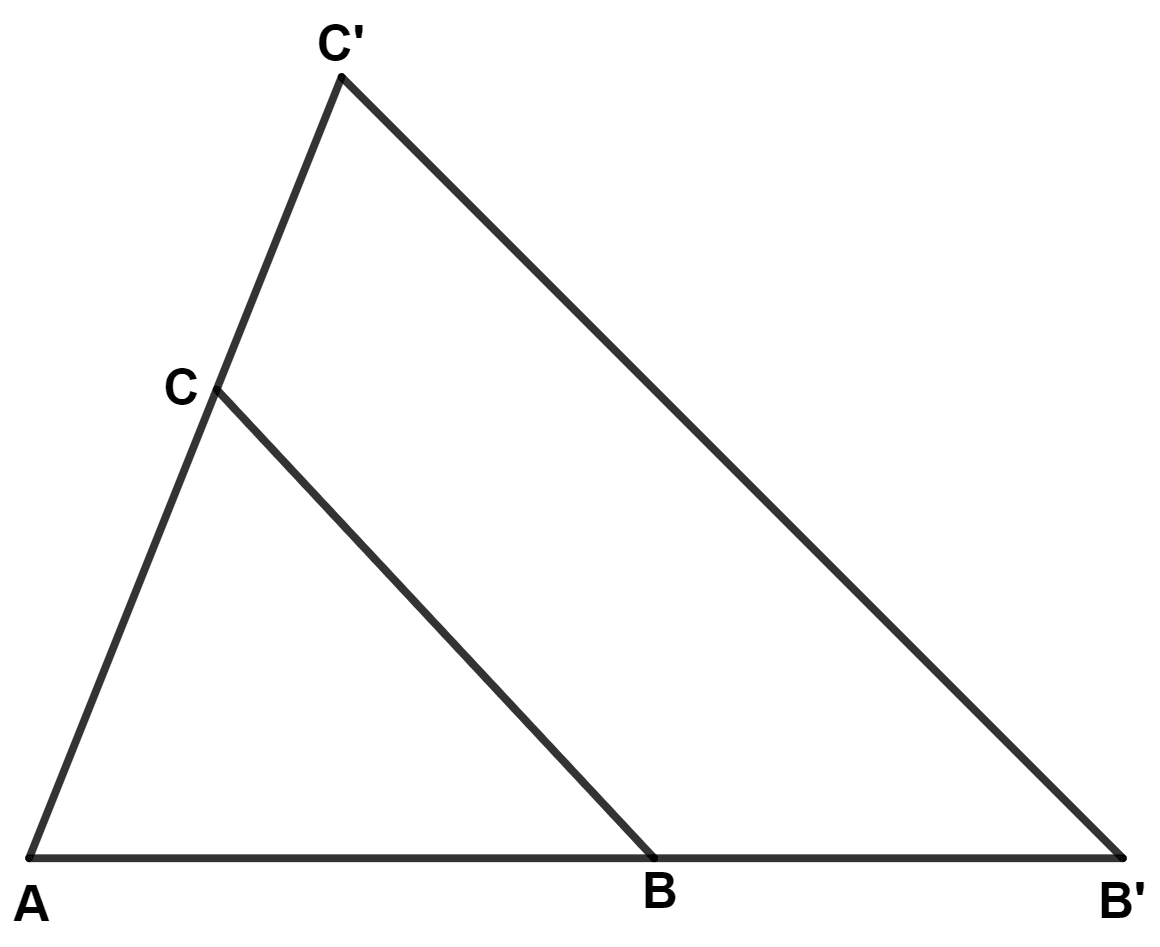
While preparing a PowerPoint presentation, ∆ ABC is enlarged along the side BC to ∆ AB'C', as shown in the diagram, such that BC ∶ B'C' is 3 ∶ 5. Find :
(a) AB ∶ BB'
(b) length AB, if BB' = 4 cm.
(c) Is ∆ ABC ~ ∆ AB'C' ? Justify your answer.
(d) ar (∆ ABC) : ar (quad. BB'C'C).
Similarity
34 Likes
Answer
Since, ∆ ABC is enlarged along the side BC to ∆ AB'C'.
∴ ∆ ABC and ∆ AB'C' are similar triangles.
(a) We know that,
Ratio of corresponding sides of similar triangles are proportional.
Let AB = 3x and AB' = 5x
From figure,
⇒ AB' = AB + BB'
⇒ 5x = 3x + BB'
⇒ BB' = 5x - 3x = 2x.
⇒ AB : BB' = 3x : 2x = 3 : 2.
Hence, AB : BB' = 3 : 2.
(b) As,
Hence, AB = 6 cm.
(c) Since, ∆ ABC is enlarged along the side BC to ∆ AB'C'.
∴ BC || B'C'
In ∆ ABC and ∆ AB'C',
⇒ ∠BAC = ∠B'AC' (Common angle)
⇒ ∠ABC = ∠AB'C' (Corresponding angle are equal)
∴ ∆ ABC ~ ∆ AB'C' (By A.A. axiom).
Hence, proved that ∆ ABC ~ ∆ AB'C'.
(d) We know that,
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Let area of ∆ ABC = 9a and area of ∆ AB'C' = 25a.
Area of quadrilateral BB'C'C = Area of ∆ AB'C' - Area of ∆ ABC = 25a - 9a = 16a.
∴ Area of ∆ ABC : Area of quadrilateral BB'C'C = 9a : 16a = 9 : 16.
Hence, area of ∆ ABC : area of quadrilateral BB'C'C = 9 : 16.
Answered By
19 Likes
Related Questions
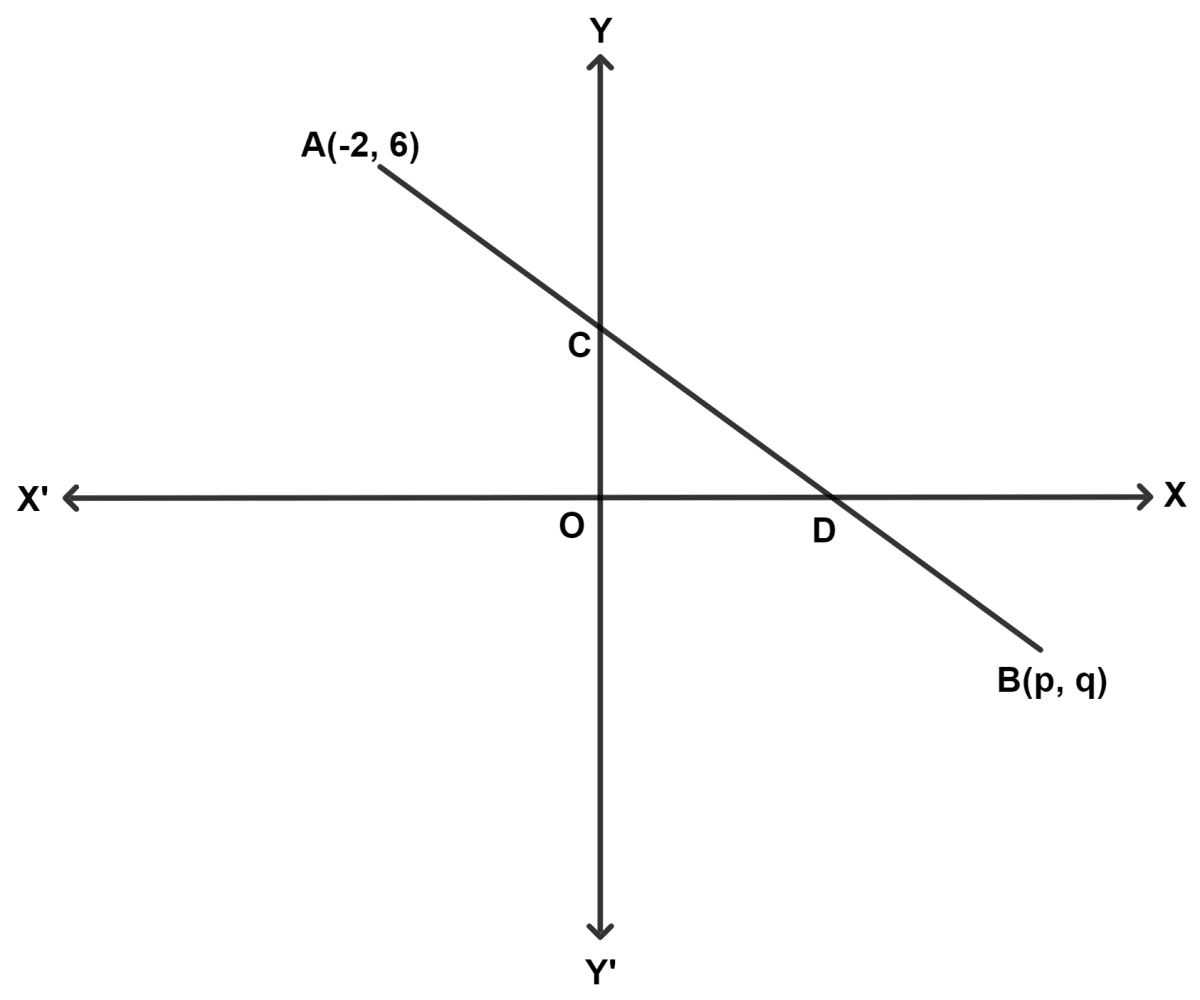
In the given figure, if the line segment AB is intercepted by the y-axis and x-axis at C and D, respectively, such that AC : AD = 1 : 4 and D is the midpoint of CB. Find the coordinates of D, C and B.
Find the equation of the straight line perpendicular to the line x + 2y = 4, which cuts an intercept of 2 units from the positive y-axis. Hence, find the intersection point of the two lines.
The approximate volume of a human eye is 6.5 cm3. The volume of a laboratory model (excluding base and stand) of the human eye is 1404 cm3.

(a) State whether the scale factor k is less than, equals to or greater than 1.
(b) Calculate the:
(i) value of k
(ii) diameter of the human eye if the radius of the model is 7.2 cm.
(iii) the external surface area of the human eye if the surface area of the model is 651.6 cm2.
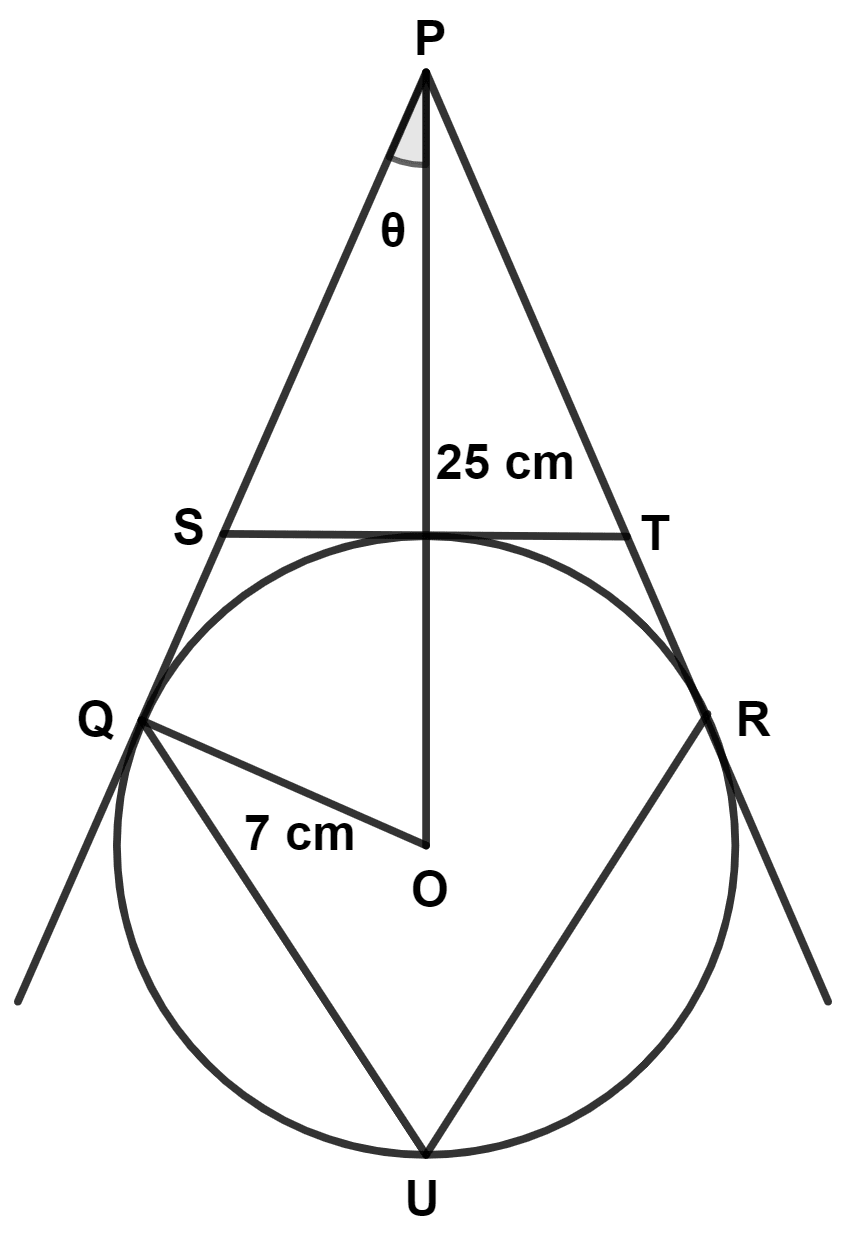
In the adjoining diagram PQ, PR and ST are the tangents to the circle with centre O and radius 7 cm. Given OP = 25 cm. Find :
(a) length of ST
(b) value of ∠OPQ, i.e. θ
(c) ∠QUR, in nearest degree