Mathematics
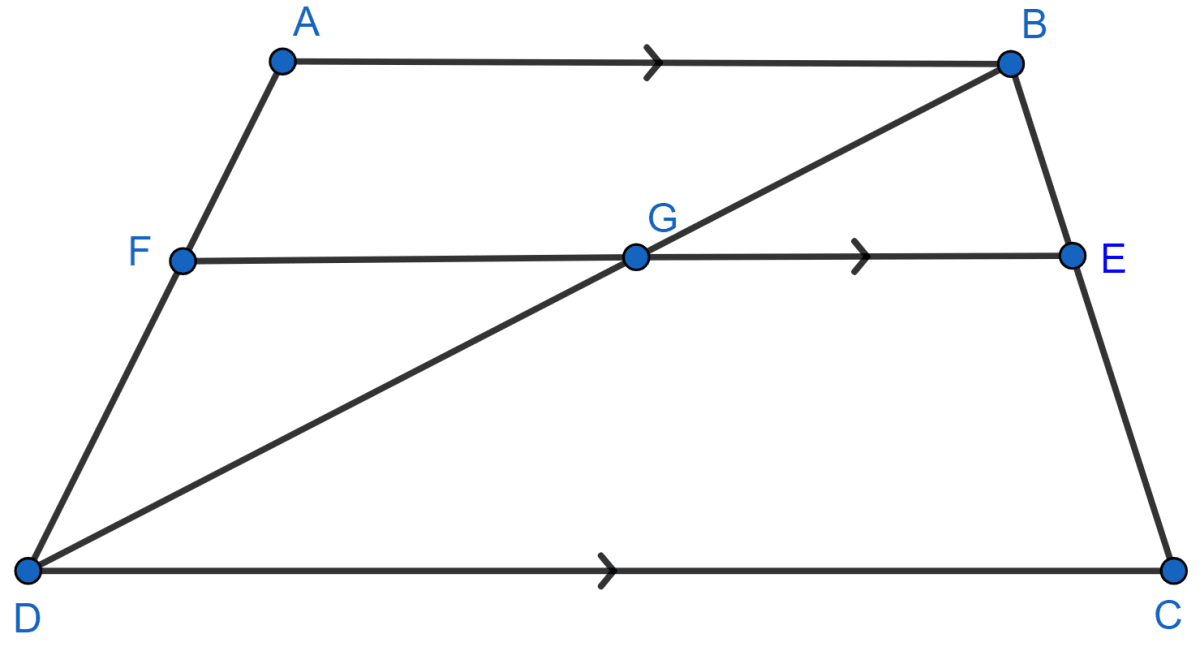
In trapezium ABCD, AB || DC and DC = 2AB. EF drawn parallel to AB cuts AD in F and BC in E such that 4 BE = 3EC. Diagonal DB intersects FE at point G. Prove that : 7EF = 10AB.
Similarity
53 Likes
Answer
Given,
⇒ 4BE = 3EC
⇒
In △DFG and △DAB,
⇒ ∠DFG = ∠DAB [As corresponding angles are equal]
⇒ ∠FDG = ∠ADB (Common)
⇒ △DFG ~ △DAB [By AA postulate]
In similar triangles,
The ratios between the lengths of corresponding sides are equal.
……….(1)
In trapezium ABCD, we have
EF || AB || DC
From (1) and (2), we get :
FG = AB ………(3)
In △BEG and △BCD,
⇒ ∠BEG = ∠BCD [As corresponding angles are equal]
⇒ ∠GBE = ∠DBC (Common angle)
⇒ △BEG ~ △BCD [By AA postulate]
In similar triangles,
The ratios between the lengths of corresponding sides are equal.
…………..(4)
Given,
Adding equation (3) and (5),
Hence, proved that 7EF = 10AB.
Answered By
32 Likes
Related Questions
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point O. If BO : OD = 4 : 7, find :
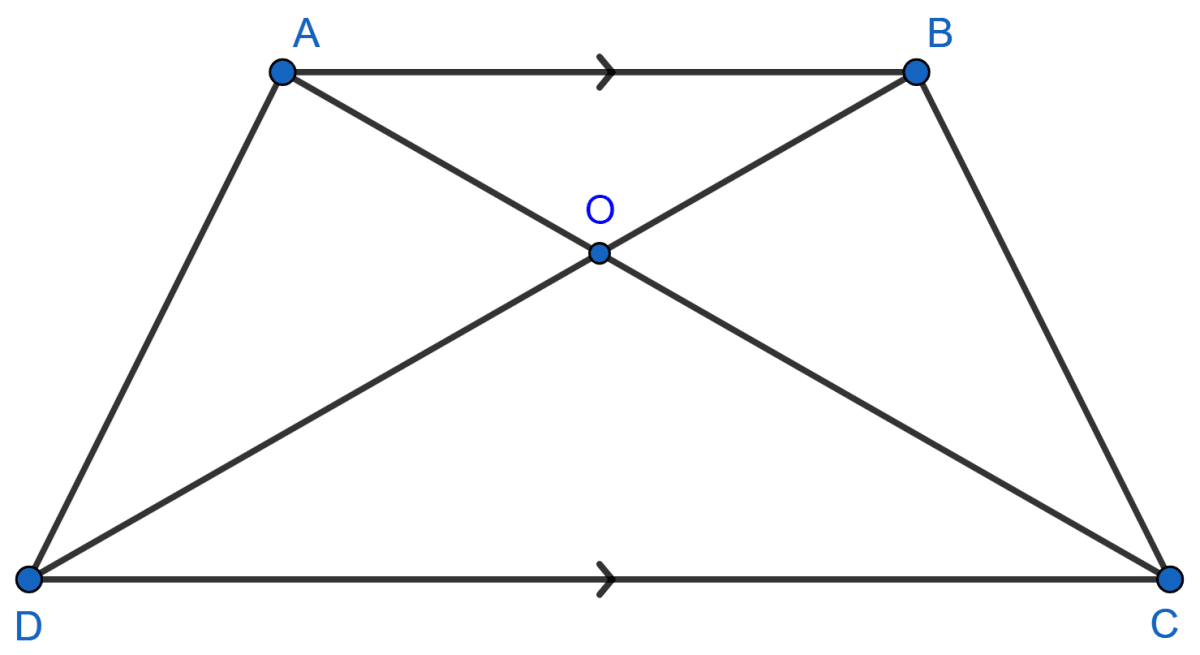
(i) △AOD : △AOB
(ii) △AOB : △ACB
(iii) △DOC : △AOB
(iv) △ABD : △BOC
A model of a ship is made to a scale of 1 : 160. Find :
(i) the length of the ship, if the length of its model is 1.2 m
(ii) the area of the deck of the ship , if the area of deck of its model is 1.2 m2.
(iii) the volume of the ship, if the volume of its model is 1.2 m3.
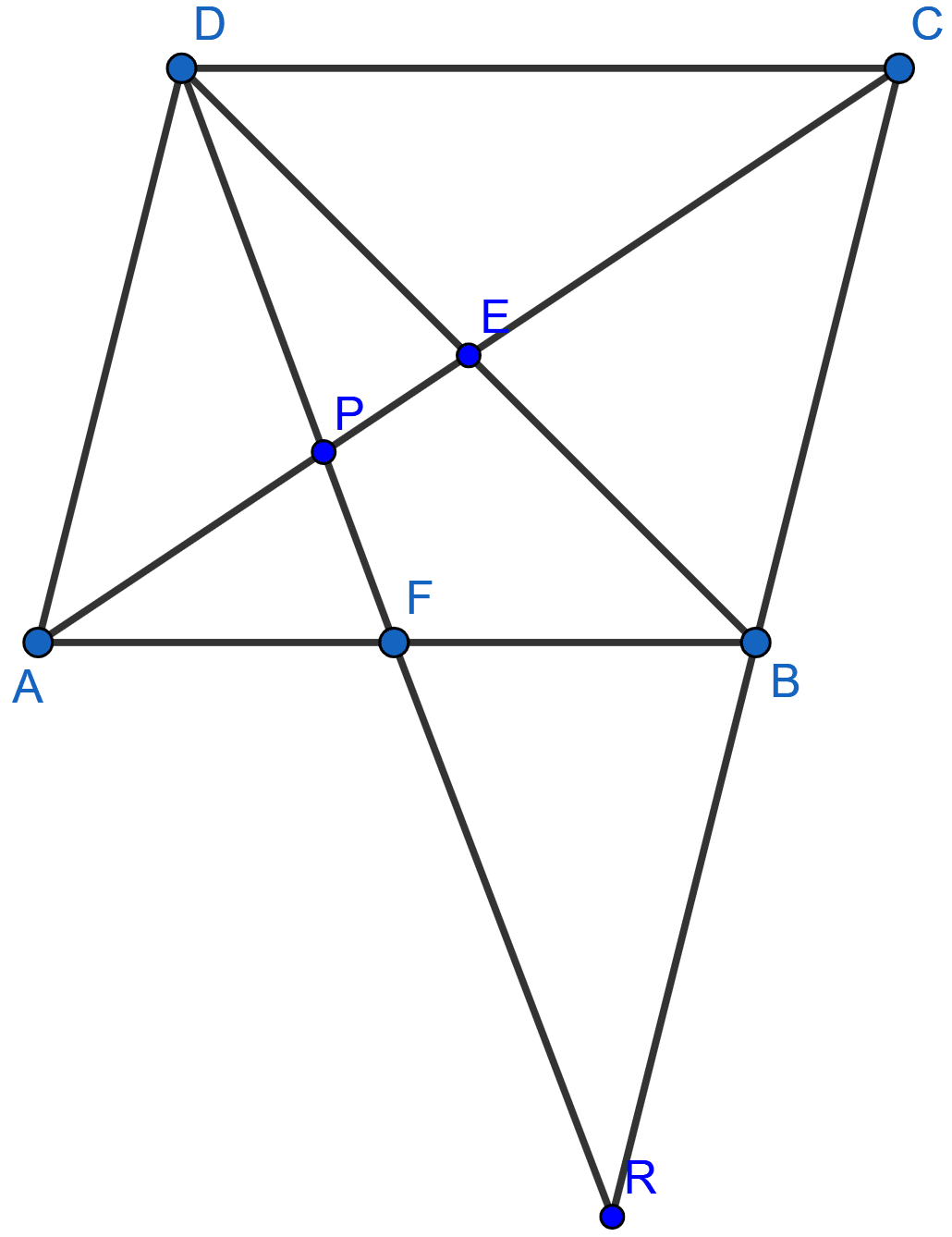
Given : ABCD is a rhombus, DPR and CBR are straight lines.
Prove that :
DP × CR = DC × PR.
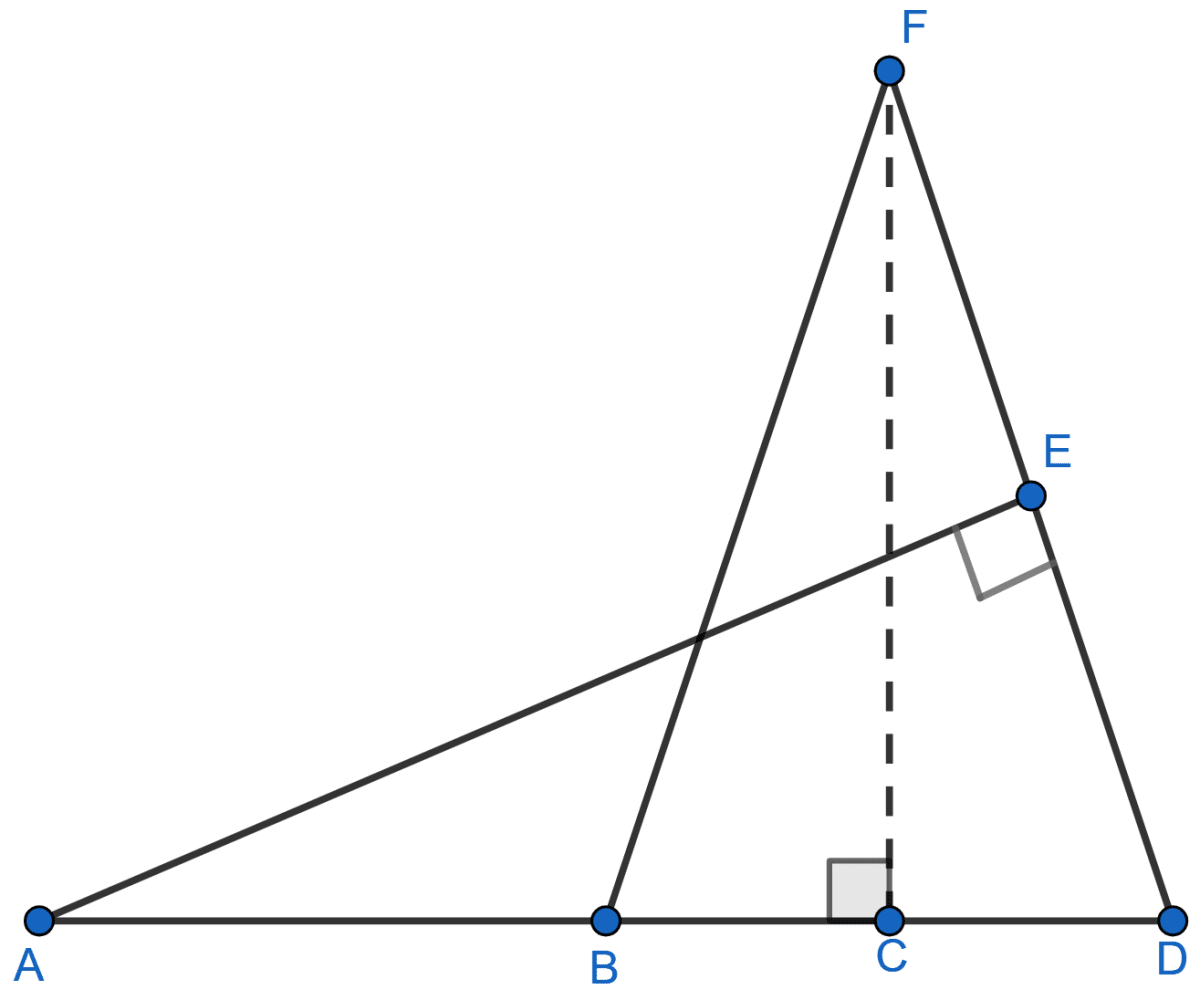
Given : FB = FD, AE ⊥ FD and FC ⊥ AD.
Prove that :