Objective Type Questions
Question 1
In Java, for an array having N elements, legal subscripts are :
- 0 to N
- 0 to N-1
- 1 to N
- 1 to N - 1
Answer
0 to N-1
Reason — In Java, for an array having N elements, the subscripts start from 0 and go on till N - 1 (size - 1).
Question 2
Total size of array A having 25 elements of char type is ............... .
- 25 bytes
- 50 bytes
- 100 bytes
- None of these
Answer
50 bytes
Reason — The size of char data type is 2 bytes. Since A is an array of char type, the size of each element of the array will be 2 bytes. The size of 25 elements will be 25 X 2 = 50 bytes.
Question 3
Total size of array B[10][5] of int type is ............... .
- 50 bytes
- 15 bytes
- 100 bytes
- 200 bytes
Answer
200 bytes
Reason — The size of int data type is 4 bytes. Since B is an array of int type, the size of each element of the array will be 4 bytes. The array has 10 rows and 5 columns, thus total number of elements will be 10 X 5 = 50. The size of 50 elements will be 50 X 4 = 200 bytes.
Question 4
Total number of elements in array C[5][3][2] are ............... .
- 10
- 20
- 30
- 50
Answer
30
Reason — The total number of elements in array C will be 5 x 3 x 2 = 30.
Question 5
Which of the following statements are valid array declaration ?
- int number( );
- float average[ ];
- double[ ] marks;
- counter int[ ];
Answer
float average[ ];
double[ ] marks;
Reason — The statements float average[ ]; and double[ ] marks; are valid as they follow the syntax for declaration of an array.
int number( ); uses small brackets () instead of square brackets []. The correct statement will be int number[];.
counter int[ ]; has exchanged the place of data type and array variable. The correct statement will be int counter[];
Question 6
Consider the following code
int number[ ] = new int[5];After execution of this statement, which of the following are True ?
- number[0] is undefined
- number[5] is undefined
- number[2] is 0
- number.length is 5
Answer
number[5] is undefined
Reason — The valid subscripts of an array of size N are from 0 to N - 1. Thus, subscripts of array number will be from 0 to 4 (5 - 1).
Question 7
Which of the following contain error ?
- int x[ ] = int[10];
- int[ ] y = new int[5];
- float d[ ] = {1, 2, 3};
- x = y = new int[10];
- int a[ ] = {1, 2}; int b[ ]; b = a;
- int i = new int(10);
Answer
int x[ ] = int[10];
x = y = new int[10];
int i = new int(10);
Reason — int x[] = int[10]; doesn't contain the 'new' keyword used to initialize an array. The correct statement will be int x[] = new int[10];
In the statement x = y = new int[10];, 'x' and 'y' are not declared as array variables. The correct statement will be :
int x[] = new int[10];
int y[] = new int[10];
In the statement int i = new int(10);, 'i' is not declared as array variable and small brackets () are used instead of square brackets []. The correct statement will be int i[] = new int[10];
The remaining statements follow the syntax used for declaring and initializing an array, thus they do not have any error.
Question 8
Given that int A[ ] = {35, 26, 19, 76, 58};
What will be value contained in A[3] ?
- 35
- 26
- 19
- 76
- 58
Answer
76
Reason — The valid subscripts of an array are from 0 to size - 1. Thus, A[0] = 35, A[1] = 26, A[2] = 19, A[3] = 76 and A[4] = 58.
Question 9
Given that int z[ ][ ] = {{2, 6, 5}, {8, 3, 9}}; What will be value of z[1][0] and z[0][2] ?
- 2 and 9
- 8 and 5
- 2 and 5
- 6 and 3
Answer
8 and 5
Reason — Two-dimensional arrays are stored in a row-column matrix, where the first index indicates the row and the second indicates the column.
The element stored at z[1][0] refers to the element stored in second row and first column, which is 8.
The element stored at z[0][2] refers to the element stored in first row and third column, which is 5.
Question 10
Given array 12, 3, 8, 5. What will be array like after two passes of selection sort ?
- 12, 3, 8, 5
- 3, 5, 8, 12
- 3, 8, 5, 12
- 3, 5, 12, 8
Answer
3, 5, 8, 12
Reason — Selection Sort is a sorting technique where next smallest (or next largest) element is found in the array and moved to its correct position in each pass.
In the first pass, smallest element 3 will be found and swapped with the first position element 12. The array elements after the first pass will be:
3, 12, 8, 5
In the second pass, the next smallest element 5 will be found and swapped with the second position element 12.The array elements after the second pass will be:
3, 5, 8, 12
Question 11
Given an array 12, 3, 8, 5. What will be array like after two passes of bubble sort?
- 12, 3, 8, 5
- 3, 8, 12, 5
- 3, 5, 8, 12
- 12, 3, 5, 8
Answer
3, 8, 12, 5
Reason — The basic idea of bubble sort is to move the largest element to the highest index position in the array. To attain this, two adjacent elements are compared repeatedly and exchanged if they are not in correct order.
In the first pass, adjacent elements (12,3) will be compared and swapped. The array will look like this after the first pass:
3, 12, 8, 5
In the second pass, adjacent elements (12,8) will be compared and swapped. The array will look like this after the second pass:
3, 8, 12, 5
Question 12
An array
18, 13, 2, 9, 5
is
13, 2, 9, 18, 5
after three passes. Which sorting technique is applied on it?
Answer
Bubble sort is applied on the array.
Explanation
In the first pass, adjacent elements (18, 13) will be compared and swapped. The array will look like this after the first pass:
13, 18, 2, 9, 5
In the second pass, adjacent elements (18, 2) will be compared and swapped. The array will look like this after the first pass:
13, 2, 18, 9, 5
In the third pass, adjacent elements (18, 9) will be compared and swapped. The array will look like this after the third pass:
13, 2, 9, 18, 5
Assignment Questions
Question 1
What do you understand by an array ? What is the significance of arrays ?
Answer
An array is a collection of variables of the same type that are referenced by a common name. It is a reference data type which stores data values in contiguous memory locations. An array is declared and initialized as follows:
int arr[] = new int[10];
The significance of arrays are as follows:
- Easy to specify — The declaration, allocation of memory space, initialization can all be done in one line of code.
- Free from run-time overheads — There is no run-time overhead to allocate/free memory, apart from once at the start and end.
- Random access of elements — Arrays facilitate random (direct) access to any element via its index or subscript.
- Fast Sequential Access — It is usually faster to sequentially access elements due to contiguous storage and constant time computation of the address of a component.
- Simple code — As arrays facilitate access of multiple data items of same type through a common name, the code becomes much simpler and easy to understand.
Question 2
What is meant by index of an element ? How are indices numbered in JAVA ?
Answer
Each element in an array is referred to by their subscript or index. The index of an element refers to the position of an element in the array. In Java, the indices start from 0 and go on till size - 1.
For example,
int arr[] = {3, 6, 8};
In the array arr[], arr[0] = 3, arr[1] = 6 and arr[2] = 8.
Question 3
Determine the total bytes required to store B[17], a char array.
Answer
A char data type requires 2 bytes in memory. So, the memory required to store 17 char elements will be 17 X 2 = 34 bytes.
Question 4
What is the data type of elements of an array called ?
Answer
The data type of elements of an array is called base type of an array.
Question 5
Arrays do not prove to be useful where quite many elements of the same data types need to be stored and processed. (T/F)
Answer
False
Reason — Arrays store same type of data elements in contiguous memory locations and under a single variable name. This makes them very useful where quite many elements of the same data types need to be stored and processed as the user can refer to the elements using the same name and different index numbers.
Question 6
A subscript of an element designates its position in the array's ordering. (T/F)
Answer
True
Reason — The index of an element determines its position in an array.
Question 7
How is one-dimensional array represented in memory ?
Answer
Single-dimensional arrays are lists of information of the same type and their elements are stored in contiguous memory locations in their index order.
For example, an array grade of type char with 8 elements declared as
char grade[ ] = new char[8];
will have the element grade[0] at the first allocated memory location, grade[1] at the next contiguous memory location, grade[2] at the next, and so forth. Since grade is a char type array, each element size is 2 bytes and it will be represented in memory as shown in the figure given below:

Question 8
Determine the number of bytes required to store an int array namely A[23].
Answer
An int data type requires 4 bytes in memory. Therefore, the storage space required by array A[ ] will be 23 x 4 = 92 bytes.
Question 9
An array element is accessed using ............... .
- a first-in-first-out approach
- the dot operator
- an element name
- an index number
Answer
an index number
Reason — An array element is accessed using the array name along with an index number, which corresponds to the position of the element in an array.
Question 10
All the elements in an array must be of ............... data type.
Answer
All the elements in an array must be of same data type.
Question 11
Write a statement that defines a one-dimensional array called amount of type double that holds two elements.
Answer
double amount[] = new double[2];Question 12
The elements of a seventy-element array are numbered from ............... to ............... .
Answer
The elements of a seventy-element array are numbered from 0 to 69.
Question 13
Element amount[9] is which element of the array ?
- the eighth
- the ninth
- the tenth
- impossible to tell.
Answer
the tenth
Reason — In Java arrays, element at position 1 has index/subscript 0, element at position 2 has index 1, element at position 3 has index 2 and so on. Thus, position of an element is [index + 1]. Hence, amount[9] (9 + 1 = 10) will be the tenth element of the array.
Question 14(i)
Declare following arrays: figures of 30 char element.
Answer
char figures[] = new char[30];Question 14(ii)
Declare following arrays: check of 100 short element.
Answer
short check[] = new short[100];Question 14(iii)
Declare following arrays: balance of 26 float element.
Answer
float balance[] = new float[26];Question 14(iv)
Declare following arrays: budget of 58 double element.
Answer
double budget[] = new double[58];Question 15
Declare an array of 5 ints and initialize it to the first five even numbers.
Answer
int even[] = {2, 4, 6, 8, 10};Question 16
Write a statement that displays the value of the second element in the long array balance.
Answer
System.out.println(balance[1]);Question 17
For a multidimensional short array X[5][24], find the number of bytes required.
Answer
The formula to calculate total number of bytes required by a two-dimensional array is as follows:
total bytes = number-of-rows x number-of-columns x size-of-base-type
= 5 x 24 x 2 (since short requires 2 bytes in memory)
= 240 bytes
Question 18
For a multidimensional array B[9][15] find the total number of elements in B.
Answer
The total number of elements in array B is as follows:
Total elements = number of rows x number of columns
= 9 x 15
= 135
Question 19
How are the 2-D arrays stored in the memory?
Answer
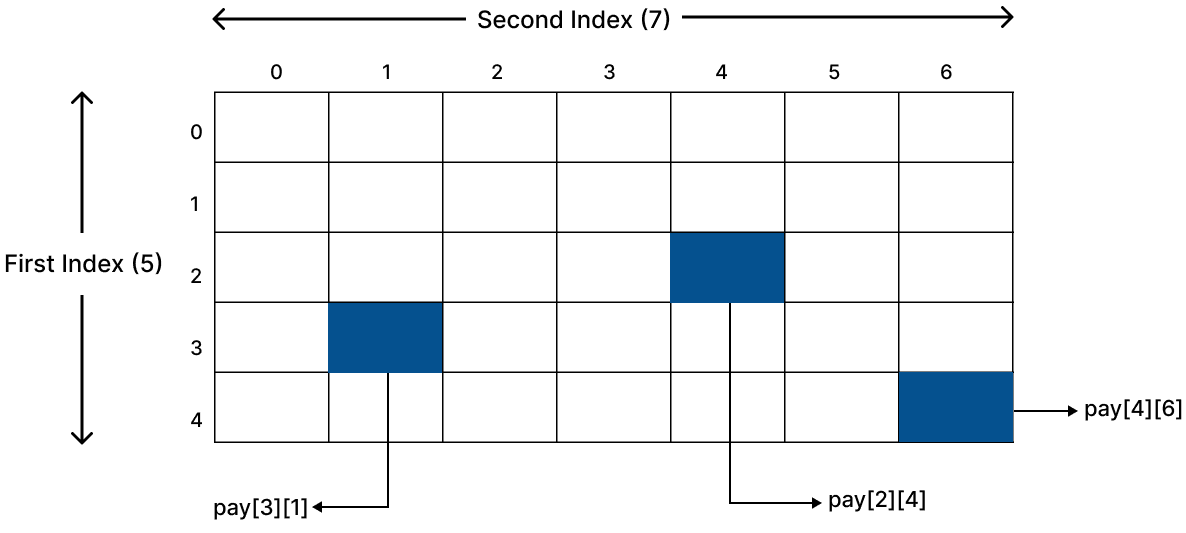
Two-dimensional arrays are stored in a row-column matrix, where the first index indicates the row and the second indicates the column.
For example, if we declare an array pay as follows:
short[][] pay = new short[5][7];
it will be having 5 x 7 = 35 elements which will be represented in memory as shown below:
Question 20
What are the preconditions for Binary Search to be performed on a single dimensional array ?
Answer
The preconditions for Binary Search to be performed on a single dimensional array are:
- The array should be sorted, either in ascending order or descending order.
- Lower bound, upper bound and the sort order of the array must be known.
Question 21(i)
A binary search of an ordered set of elements in an array is always faster than a sequential search of the elements. True or False ?
Answer
False
Reason — In a case where the search item is at the first place in a sorted array, sequential search becomes faster than binary search as the first comparison yields the desired value. In case of binary search, the search value is found after some passes are finished.
For example, let us consider an array arr[] = {2, 5, 8, 12} and the search value = 2. In this case, sequential search will find the search value in the first comparison while binary search will first compare the search value with the mid value i.e. 5 and continue its passes.
Question 21(ii)
A binary search of elements in an array requires that the elements be sorted from smallest to largest. True or False ?
Answer
False
Reason — A binary search requires a sorted array. It may be in ascending order or descending order.
Question 21(iii)
The performance of linear search remains unaffected if an unordered array is sorted in ascending order. True or False ?
Answer
True
Reason — Linear search is not affected if an unordered array is sorted in ascending order.
Question 21(iv)
For inserting of an element in a sorted array, the elements are always shifted to make room for the new entrant. True or False ?
Answer
True
Reason — For inserting of an element in a sorted array, the elements are always shifted to make room for the new entrant, the only exception being when the element is inserted at the end of the array.
Question 22
Name some commonly used sorting techniques.
Answer
Some commonly used sorting techniques are:
- Selection sort
- Bubble sort
- Shell sort
- Shuttle sort
- Quick sort
- Heap sort
Question 23
Show the contents of the array after the second iteration of Selection Sort.
Answer
In the first iteration, the smallest element 1 will be swapped with the element at first index 12. The contents of the array after the first iteration of Selection Sort will be:
In the second iteration, the second smallest element 2 will be swapped with the element at second index 7. The contents of the array after the second iteration of Selection Sort will be:
Question 24
Show the contents of the array after the second iteration of Bubble Sort.
Answer
In the first iteration, (35,6) will be compared and swapped. The array after the first iteration will look like:
In the second iteration, (35,8) will be compared and swapped. After the second iteration, the array will look like:
Question 25
What is the difference between linear search and binary search ?
Answer
| Linear Search | Binary Search |
|---|---|
| Linear search works on sorted and unsorted arrays. | Binary search works only on sorted arrays (both ascending and descending). |
| Each element of the array is checked against the target value until the element is found or end of the array is reached. | Array is successively divided into 2 halves and the target element is searched either in the first half or in the second half. |
| Linear Search is slower. | Binary Search is faster. |
Question 26
Given the following array :
Which sorting algorithm would produce the following result after three iterations
Answer
Selection sort algorithm
Reason — We can see that after three iterations the first three elements of the array are in their correct positions. This happens in Selection sort. In Bubble sort, the heaviest element settles at its appropriate position in the bottom i.e., the array is sorted from the end to the start.
Details of each iteration are captured below:
Array after the first iteration:
Array after the second iteration:
Array after the third iteration:
Question 27
Given the following array :
Which sorting algorithm would produce the following result after three iterations.
Answer
Bubble sort algorithm
Reason — In bubble sort, the adjoining values are compared and exchanged if they are not in proper order. This process is repeated until the entire array is sorted.
In the first pass, (13,19) will be compared but not swapped. The array after the first pass will be:
In the second pass, (19, 6) will be compared and swapped. The array after the second pass will be:
In the third pass, (19, 2) will be compared and swapped. The array after the third pass will be:
Question 28
What is an array ? What is the need for arrays ?
Answer
An array is a collection of variables of the same type that are referenced by a common name. It is a reference data type which stores data values in contiguous memory locations. An array is declared and initialized as follows:
int arr[] = new int[10];
The use of arrays have the following benefits:
- Easy to specify — The declaration, allocation of memory space, initialization can all be done in one line of code.
- Free from run-time overheads — There is no run-time overhead to allocate/free memory, apart from once at the start and end.
- Random access of elements — Arrays facilitate random (direct) access to any element via its index or subscript.
- Fast Sequential Access — It is usually faster to sequentially access elements due to contiguous storage and constant time computation of the address of a component.
- Simple code — As arrays facilitate access of multiple data items of same type through a common name, the code becomes much simpler and easy to understand.
Question 29
What are different types of arrays? Give examples of each array type.
Answer
Arrays are of different types :
- One-dimensional array — It comprises of finite homogeneous elements.
- Multi-dimensional arrays — It comprises of elements, each of which is itself an array. A two-dimensional array is the simplest of multidimensional arrays, having two indices (rows and columns).
Question 30
Write a note on how single-dimension arrays are represented in memory.
Answer
Single-dimensional arrays are lists of information of the same type and their elements are stored in contiguous memory locations in their index order.
Internally, arrays are stored as a special object containing :
- A group of contiguous memory locations that all have the same name and same datatype.
- A reference that stores the beginning address of the array elements.
- A separate instance variable containing the number of elements in the array.
For example, an array grade of type char with 8 elements declared as
char grade[ ] = new char[8];
will have the element grade[0] at the first allocated memory location, grade[1] at the next contiguous memory location, grade[2] at the next, and so forth. Since grade is a char type array, each element size is 2 bytes and it will be represented in memory as shown in the figure given below:

Question 31
How does the amount of storage (in bytes) depend upon type and size of an array? Explain with the help of an example.
Answer
The amount of storage depends upon the type and size of an array as every data type requires different storage space in memory and the number of elements (size) of an array determines how many memory blocks of same size are required.
To calculate the amount of storage required by an array we use the formula:Size = size of data type x number of elements in an array
For example, int arr[] = new int[10]; will require 4 x 10 = 40 bytes space in memory.
Question 32
What do you understand by two-dimensional arrays ? State some situations that can be easily represented by two-dimensional arrays.
Answer
A two-dimensional array is an array in which each element is itself an array. For instance, an array A[M][N] is an M by N table with M rows and N columns containing M x N elements.
The general form of a two-dimensional array declaration in Java is as follows:type array-name[ ][ ] = new type[rows][columns];
Some situations that can be easily represented by two-dimensional arrays are as follows:
- In a school, marks obtained by a student in various subjects can be stored in a two-dimensional array, where rows can be used for successive tests (mid term, quarterly, half yearly etc.) and columns can be used for subjects (maths, english, science, hindi, computer etc.).
- In a business, the sales for a month can easily be represented using a two-dimensional array, where rows can represent weeks and columns can represent the individual days in a week.
Question 33
How are two-dimensional arrays represented in memory ?
Answer
Two-dimensional arrays are stored in a row-column matrix, where the first index indicates the row and the second indicates the column.
For example, if we have declared an array pay as follows:short[][] pay = new short[5][7];
it will be having 5 x 7 = 35 elements which will be represented in memory as shown below :

The amount of storage required to hold a two-dimensional array is also dependent upon its base type, number of rows and number of columns. The formula to calculate total number of bytes required by a two-dimensional array is given below :
total bytes = number-of-rows x number-of-columns x size-of-base-type
Here, the array pay[][] will require 5 x 7 x 2 = 70 bytes of memory space, as the size of a byte type element is 2 bytes.
Question 34
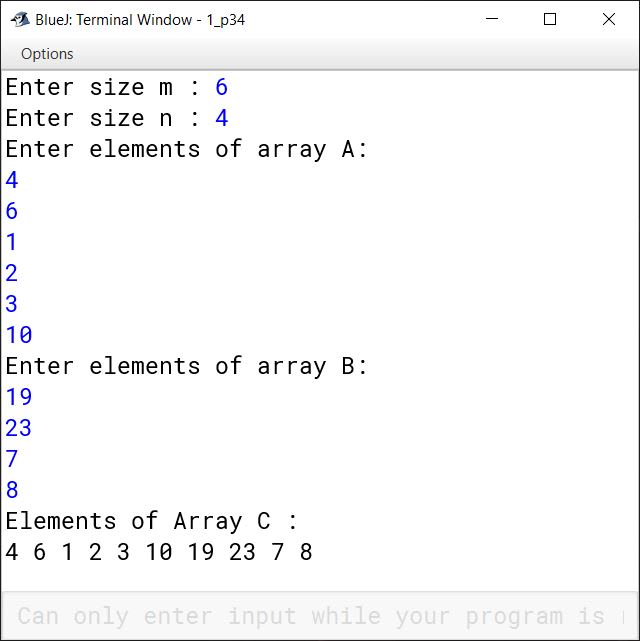
Suppose A, B, C are arrays of integers of sizes m, n, m + n respectively. Give a program to produce a third array C, containing all the data of array A and B.
import java.util.Scanner;
public class KboatArrayMerge
{
public static void main(String args[]){
Scanner in = new Scanner(System.in);
System.out.print("Enter size m : ");
int m = in.nextInt();
int A[] = new int[m];
System.out.print("Enter size n : ");
int n = in.nextInt();
int B[] = new int[n];
int C[] = new int[m + n];
System.out.println("Enter elements of array A:");
for(int i = 0; i < m; i++) {
A[i] = in.nextInt();
}
System.out.println("Enter elements of array B:");
for(int i = 0; i < n; i++) {
B[i] = in.nextInt();
}
int idx = 0;
while(idx < A.length) {
C[idx] = A[idx];
idx++;
}
int j = 0;
while(j < B.length) {
C[idx++] = B[j++];
}
System.out.println("Elements of Array C :");
for(int i = 0; i < C.length; i++) {
System.out.print(C[i] + " ");
}
}
}Output
Question 35
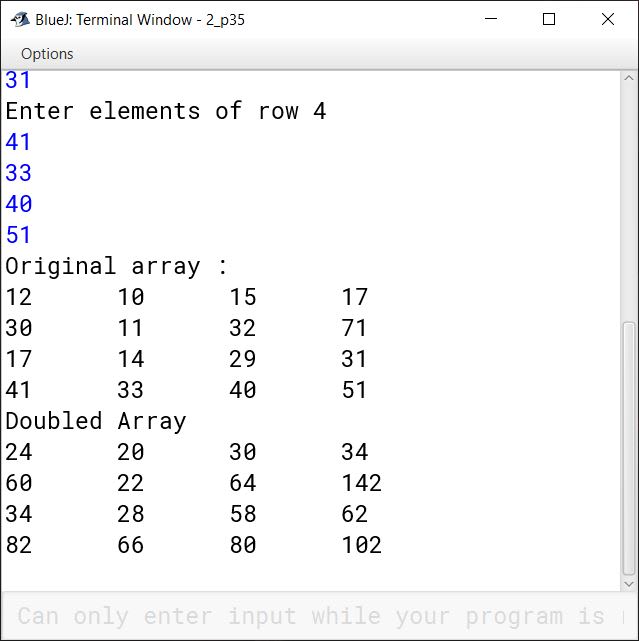
Write a short program that doubles every element of an array A[4][4].
import java.util.Scanner;
public class KboatDDADouble
{
public static void main(String args[]){
Scanner in = new Scanner(System.in);
int A[][] = new int[4][4];
System.out.println("Enter elements of 4 x 4 array");
for(int i = 0; i < 4; i++)
{
System.out.println("Enter elements of row " + (i+1));
for(int j = 0; j < 4; j++)
{
A[i][j] = in.nextInt();
}
}
System.out.println("Original array :");
for(int i = 0; i < 4; i++)
{
for(int j = 0; j < 4; j++)
{
System.out.print(A[i][j] + "\t");
}
System.out.println();
}
for(int i = 0; i < 4; i++)
{
for(int j = 0; j < 4; j++)
{
A[i][j] = A[i][j] * 2;
}
}
System.out.println("Doubled Array");
for(int i = 0; i < 4; i++)
{
for(int j = 0; j < 4; j++)
{
System.out.print(A[i][j] + "\t");
}
System.out.println();
}
}
}Output
Question 36
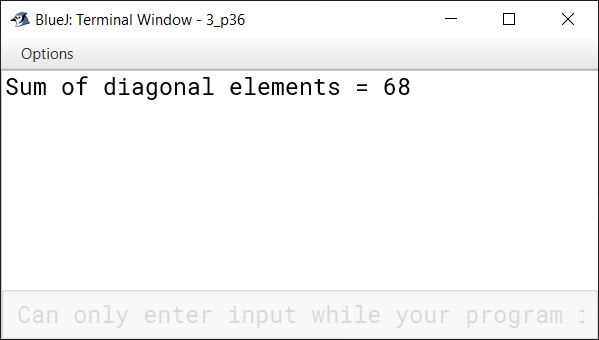
Let A(n x n) that are not diagonal array. Write a program to find the sum of all the elements which lie on either diagonal. For example, for the matrix shown below, your program should output 68 = (1 + 6 + 11 + 16 + 4 + 7 + 10 + 13):
import java.util.Scanner;
public class KboatDDADiagonalSum
{
public static void main(String args[]){
int A[][] = {{1, 2, 3, 4} ,
{5, 6, 7, 8} ,
{9, 10, 11, 12} ,
{13, 14, 15, 16}};
int sum = 0;
for(int i = 0; i < 4; i++) {
for(int j = 0; j < 4; j++) {
if (i == j || (i + j) == 3) {
sum += A[i][j];
}
}
}
System.out.println("Sum of diagonal elements = " + sum);
}
}Output
Question 37
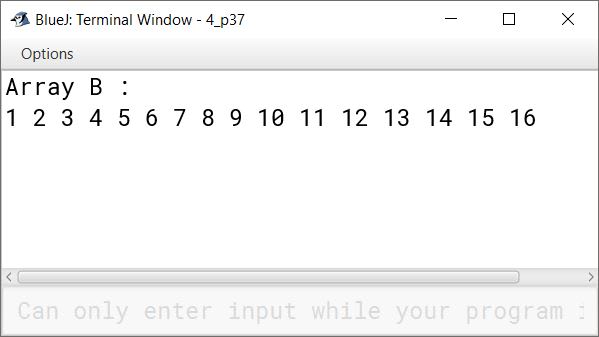
From a two-dimensional array A[4][4], write a program to prepare a one-dimensional array B[16] that will have all the elements of A if they are stored in row-major form. For example, for the following array
the resultant array should be : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
import java.util.Scanner;
public class Kboat2Dto1DArray
{
public static void main(String args[]){
int A[][] = {{1, 2, 3, 4} ,
{5, 6, 7, 8} ,
{9, 10, 11, 12} ,
{13, 14, 15, 16}};
int B[] = new int[16];
int index = 0;
for(int i = 0; i < 4; i++)
{
for(int j = 0; j < 4; j++)
{
B[index++] = A[i][j];
}
}
System.out.println("Array B :");
for(int i = 0; i < 16; i++)
{
System.out.print(B[i] + " ");
}
}
}Output
Question 38
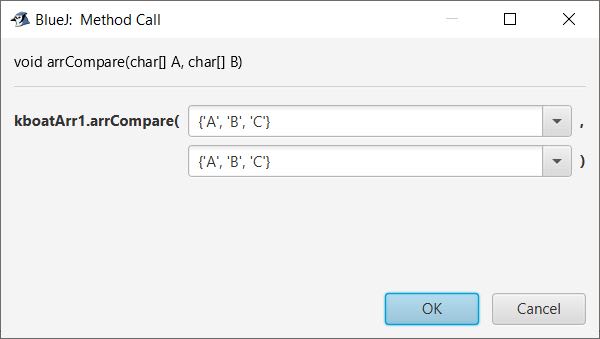
Write a function that checks whether or not two arrays (of characters) are identical, that is, whether they have same characters and all characters in corresponding positions are equal.
public class KboatArrCompare
{
public void arrCompare (char A[], char B[])
{
int l1 = A.length;
int l2 = B.length;
boolean flag = true;
if (l1 == l2) {
for(int i = 0; i < l1; i++) {
if(A[i] != B[i]) {
flag = false;
break;
}
}
}
else {
flag = false;
}
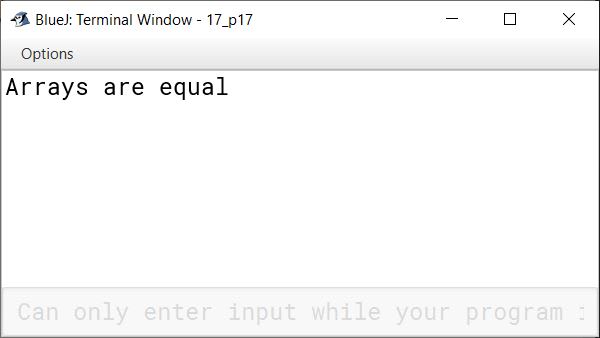
if (flag) {
System.out.println("Arrays are equal");
}
else {
System.out.println("Arrays are not equal");
}
}
}Output
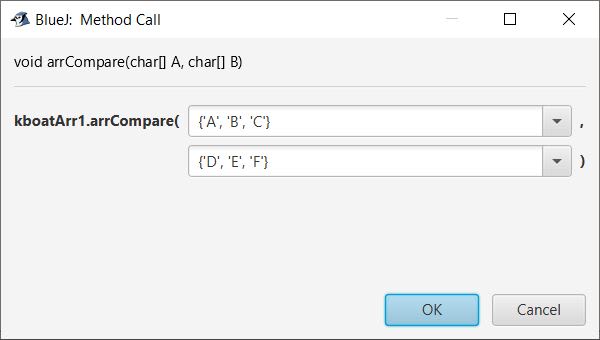
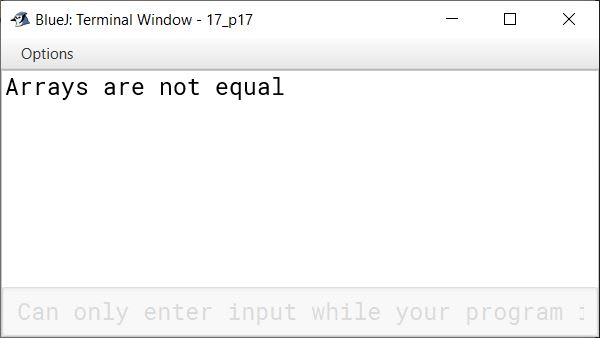
Question 39
The marks obtained by 50 students in a subject are tabulated as follows :
| Name | Marks |
|---|---|
| . | . |
| . | . |
| . | . |
Write a program to input the names and marks of the students in the subject. Calculate and display:
(i) The subject average marks (subject average marks = subject total / 50 )
(ii) The highest marks in the subject and the name of the student. (The maximum marks in the subject are 100)
import java.util.Scanner;
public class KboatSDAMarks
{
public static void main(String args[]) {
final int TOTAL_STUDENTS = 50;
Scanner in = new Scanner(System.in);
String name[] = new String[TOTAL_STUDENTS];
int marks[] = new int[TOTAL_STUDENTS];
int total = 0;
for (int i = 0; i < name.length; i++) {
System.out.print("Enter name of student " + (i+1) + ": ");
name[i] = in.nextLine();
System.out.print("Enter marks of student " + (i+1) + ": ");
marks[i] = in.nextInt();
total += marks[i];
in.nextLine();
}
double avg = (double)total / TOTAL_STUDENTS;
System.out.println("Subject Average Marks = " + avg);
int hIdx = 0;
for (int i = 1; i < marks.length; i++) {
if (marks[i] > marks[hIdx])
hIdx = i;
}
System.out.println("Highest Marks = " + marks[hIdx]);
System.out.println("Name = " + name[hIdx]);
}
}Output
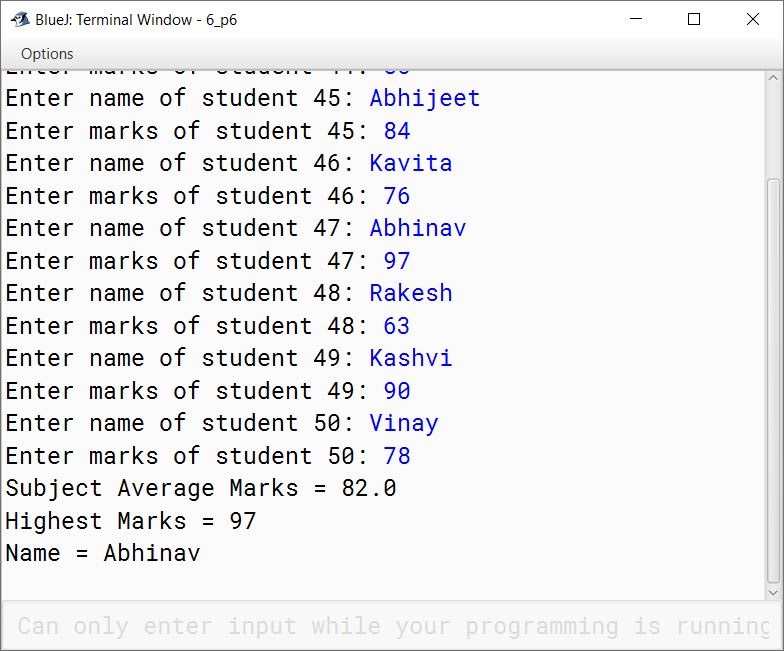
Question 40
Differentiate between one-dimensional and two-dimensional arrays.
Answer
| One-dimensional array | Two-dimensional array |
|---|---|
| One-dimensional array stores data in a single row or column. | Two-dimensional array stores data in a grid or table, with rows and columns. |
| It uses one index to access array elements. | It uses two indices to access array elements. |
For example,int arr[] = new int[10];It creates a one dimensional array arr which stores 10 elements of int type. | For example,int arr[][] = new int [3][3];It creates a two dimensional array which has three rows and three columns to store 3 x 3 = 9 elements of int type. |
Question 41
Explain
(i) Linear search method,
(ii) Binary search method.
Which of the two is more efficient for sorted data ?
Answer
(i) Linear Search — Linear Search refers to the searching technique in which each element of an array is compared with the search item, one by one, until the search-item is found or all elements have been compared.
For example, consider an array
int arr[] = {5, 8, 11, 2, 9};
and the search item 2. Linear search will compare each element of the array to 2 sequentially until either the search value 2 is found or all the elements have been compared.
(ii) Binary search — Binary Search is a search-technique that works for sorted arrays. Here search-item is compared with the middle element of array. If the search-item matches with the element, search finishes. If search-item is less than middle (in ascending array), we perform binary-search in the first half of the array, other wise we perform binary search in the second half of the array.
For example, consider an array
int arr[] = {2, 5, 8, 11, 14};
and the search item 11. First, the search value will be compared with the middle value 8. Since the values are not equal, binary search will be performed in the latter half of the array, i.e., {11, 14}. The search value will be compared with the mid value, which will be 11. Since search value is found, binary search will stop.
Binary search is more efficient than linear search as it searches the given item in minimum possible comparisons.
Question 42
Write a program Lower-left-half which takes a two dimensional array A, with size N rows and N columns as argument and prints the lower left-half.
2 3 1 5 0
7 1 5 3 1
e.g.,If A is 2 5 7 8 1
0 1 5 0 1
3 4 9 1 5
2
7 1
The output will be 2 5 7
0 1 5 0
3 4 9 1 5
import java.util.Scanner;
public class KboatLowerLeftHalf
{
public static void main(String args[]){
Scanner in = new Scanner(System.in);
System.out.print("Enter size of 2D array :" );
int n = in.nextInt();
int A[][] = new int[n][n];
System.out.println("Enter array elements : ");
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
{
A[i][j] = in.nextInt();
}
}
System.out.println("Original array :" );
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
{
System.out.print(A[i][j] + " ");
}
System.out.println();
}
System.out.println("Lower Left Half array :" );
for(int i = 0; i < n; i++)
{
for(int j = 0; j <= i; j++)
{
System.out.print(A[i][j] + " ");
}
System.out.println();
}
}
}Output
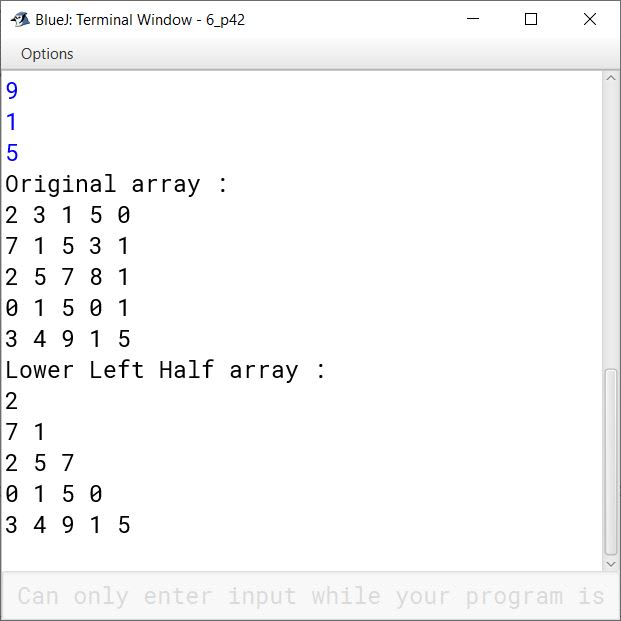
Question 43
Write a program to search for an ITEM linearly in array X[10].
Answer
import java.util.Scanner;
public class KboatLinearSearch
{
public static void main(String args[]){
Scanner in = new Scanner(System.in);
int X[] = new int[10];
int i = 0;
System.out.println("Enter array elements : ");
for(i = 0; i < 10; i++)
{
X[i] = in.nextInt();
}
System.out.println("Input Array is:");
for (i = 0; i < 10; i++) {
System.out.print(X[i] + " ");
}
System.out.println();
System.out.print("Enter ITEM to search : ");
int item = in.nextInt();
for (i = 0; i < 10; i++) {
if (X[i] == item) {
break;
}
}
if (i == 10) {
System.out.println("Search Unsuccessful");
}
else {
System.out.println("Search Successful");
System.out.println(item + " is present at index " + i);
}
}
}Output
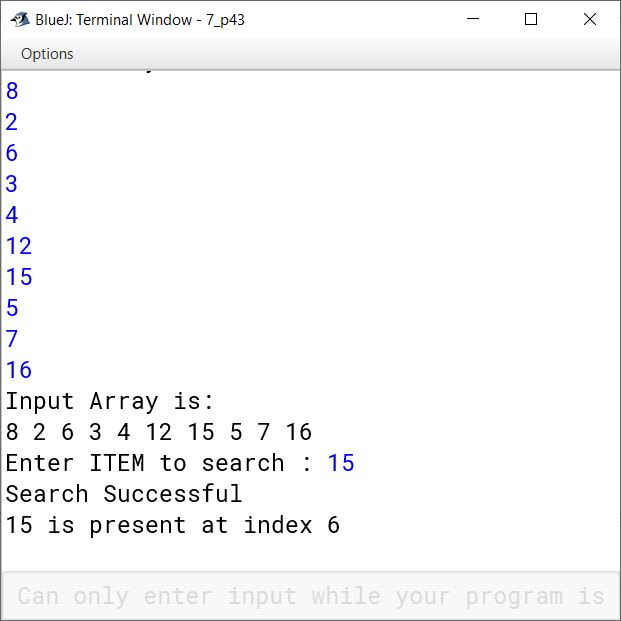
Question 44
Write a program to search for an ITEM using binary search in array X[10].
import java.util.Scanner;
public class KboatBinarySearch
{
public static void main(String args[]){
Scanner in = new Scanner(System.in);
int X[] = new int[10];
System.out.println("Enter array in ascending order : ");
for(int i = 0; i < 10; i++)
{
X[i] = in.nextInt();
}
System.out.println("Input Array is:");
for (int i = 0; i < 10; i++) {
System.out.print(X[i] + " ");
}
System.out.println();
System.out.println("Enter search item :" );
int item = in.nextInt();
int l = 0, h = 9, index = -1;
while (l <= h) {
int m = (l + h) / 2;
if (X[m] < item)
l = m + 1;
else if (X[m] > item)
h = m - 1;
else {
index = m;
break;
}
}
if (index == -1) {
System.out.println("Search item not found");
}
else {
System.out.println(item + " found at index " + index);
}
}
}Output
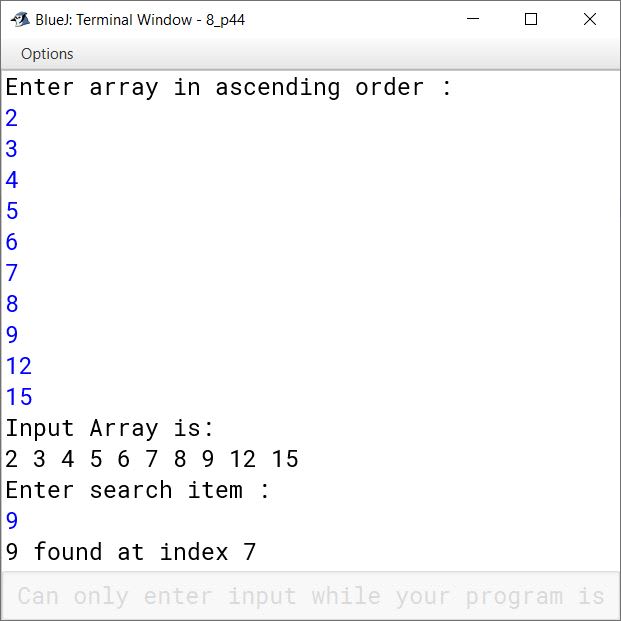
Question 45
The following array of integers is to be arranged in ascending order using the bubble sort technique:
26 21 20 23 29 17
Give the contents of the array at the end of each iteration. Do not write the algorithm.
Answer
The contents of the array at the end of each iteration are as follows:
Itr 1 — 26, 21, 20, 23, 29, 17
Itr 2 — 21, 26, 20, 23, 29, 17
Itr 3 — 21, 20, 26, 23, 29, 17
Itr 4 — 21, 20, 23, 26, 29, 17
Itr 5 — 21, 20, 23, 26, 29, 17
Itr 6 — 21, 20, 23, 26, 17, 29
Itr 7 — 20, 21, 23, 26, 17, 29
Itr 8 — 20, 21, 23, 26, 17, 29
Itr 9 — 20, 21, 23, 26, 17, 29
Itr 10 — 20, 21, 23, 17, 26, 29
Itr 11 — 20, 21, 23, 17, 26, 29
Itr 12 — 20, 21, 23, 17, 26, 29
Itr 13 — 20, 21, 17, 23, 26, 29
Itr 14 — 20, 21, 17, 23, 26, 29
Itr 15 — 20, 17, 21, 23, 26, 29
Itr 16 — 17, 20, 21, 23, 26, 29
Question 46
Write a program to search for a given ITEM in a given array X[n] using linear search technique. If the ITEM is found, move it at the top of the array. If the ITEM is not found, insert it at the end of the array.
import java.util.Scanner;
public class KboatLinearSearch
{
public static void main(String args[]) {
Scanner in = new Scanner(System.in);
System.out.print("Enter size of array : ");
int n = in.nextInt();
int X[] = new int[n];
int B[];
System.out.println("Enter array elements : ");
for(int i = 0; i < n; i++) {
X[i] = in.nextInt();
}
System.out.println("Enter search item :" );
int item = in.nextInt();
int i = 0;
// linear search
for (i = 0; i < n; i++) {
if (X[i] == item) {
System.out.println("Search item found at index "
+ i);
break;
}
}
// item not found
if (i == n) {
System.out.println("Search item not found");
B = new int[n + 1];
for(int j = 0; j < n; j++) {
B[j] = X[j];
}
B[n] = item;
System.out.println("Array after inserting "
+ item + " at end:");
for(int j = 0; j <= n; j++) {
System.out.print(B[j] + " ");
}
}
// item found
else {
for(int j = i; j >= 1; j--) {
X[j] = X[j - 1];
}
X[0] = item;
System.out.println("Array after moving "
+ item + " to top :");
for(int j = 0; j < n; j++) {
System.out.print(X[j] + " ");
}
}
}
}Output
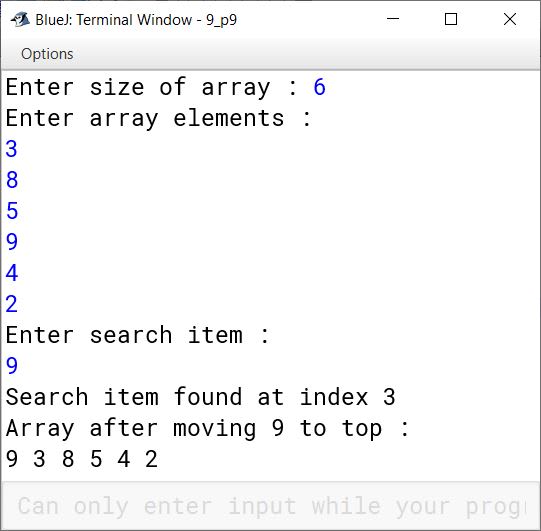
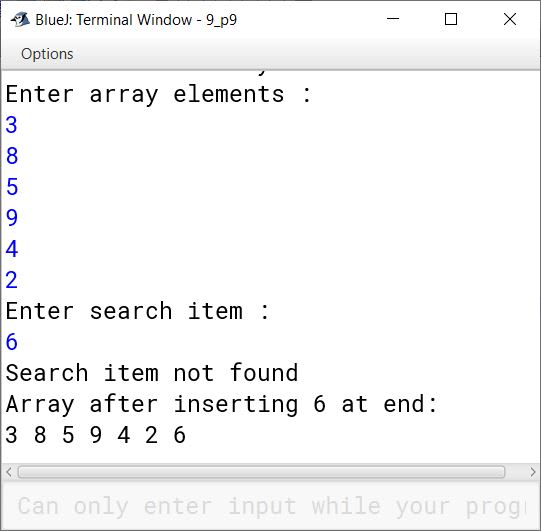
Question 47
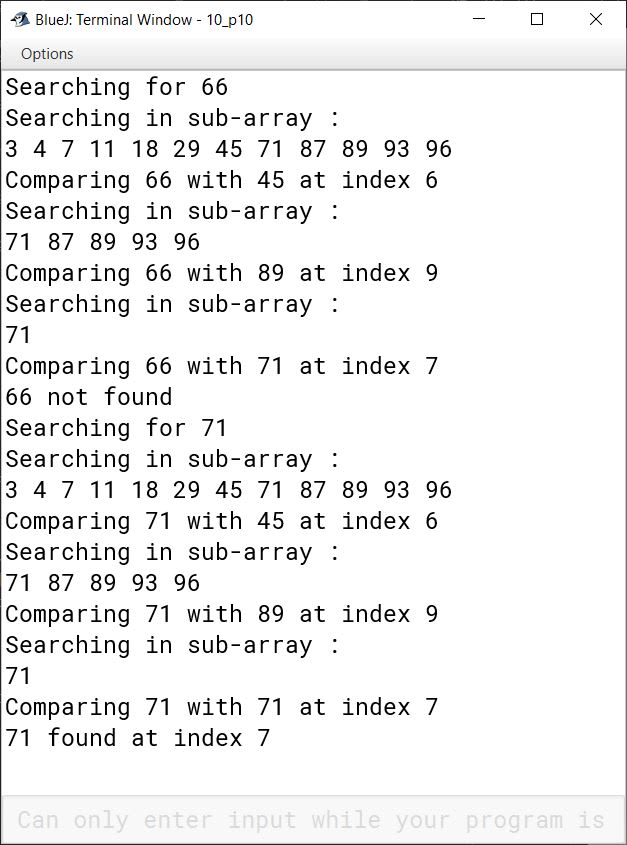
Write a program to search for 66 and 71 in the following array :
Make use of binary search technique. Also give the intermediate results while executing this algorithm.
public class KboatBinarySearch
{
public int binSearch(int arr[], int item) {
int l = 0, index = -1;
int h = arr.length - 1;
System.out.println("Searching for " + item);
while (l <= h) {
int m = (l + h) / 2;
System.out.println("Searching in sub-array :");
for(int i = l; i < h; i++)
System.out.print(arr[i] + " ");
System.out.println();
System.out.println("Comparing " + item + " with "
+ arr[m] + " at index " + m);
if (arr[m] < item)
l = m + 1;
else if (arr[m] > item)
h = m - 1;
else {
index = m;
break;
}
}
return index;
}
public static void main(String args[]) {
KboatBinarySearch obj = new KboatBinarySearch();
int X[] = {3, 4, 7, 11, 18, 29, 45, 71, 87, 89, 93, 96, 99};
int index = obj.binSearch(X, 66);
if (index == -1) {
System.out.println("66 not found");
}
else {
System.out.println("66 found at index " + index);
}
index = obj.binSearch(X, 71);
if (index == -1) {
System.out.println("71 not found");
}
else {
System.out.println("71 found at index " + index);
}
}
}Output
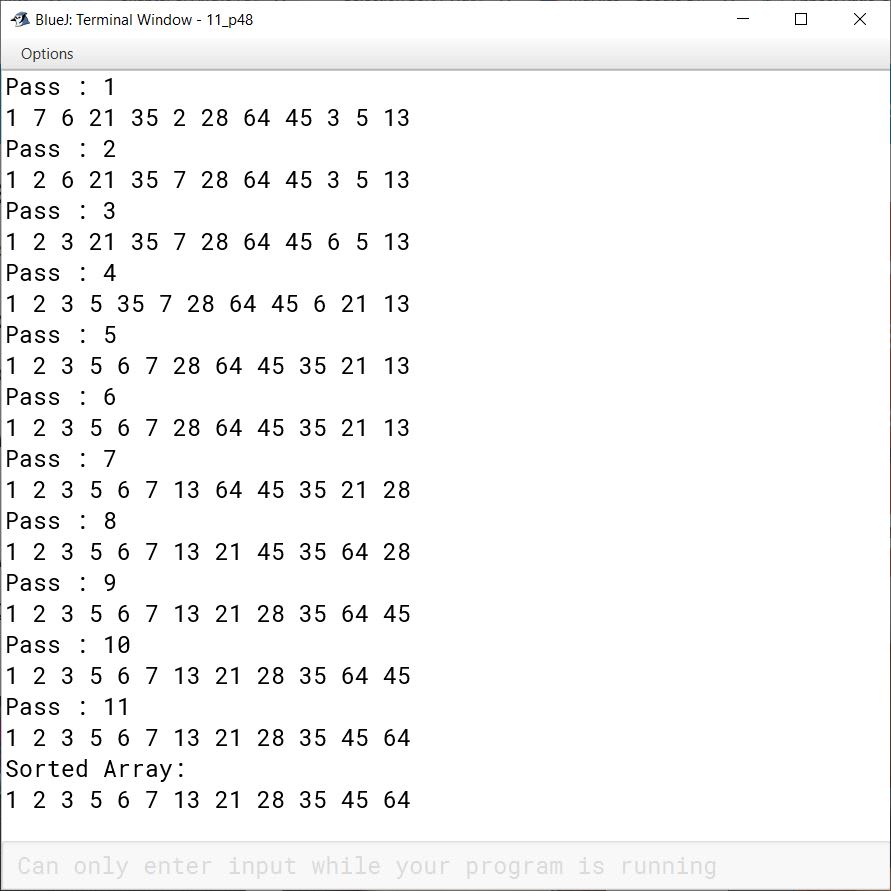
Question 48
Given the following array :
Write a program to sort the above array using exchange selection sort. Give the array status after every iteration.
public class KboatSelectionSort
{
public static void main(String args[]) {
int X[] = {13, 7, 6, 21, 35, 2, 28, 64, 45, 3, 5, 1};
int n = X.length;
for (int i = 0; i < n - 1; i++) {
int idx = i;
for (int j = i + 1; j < n; j++) {
if (X[j] < X[idx])
idx = j;
}
int t = X[i];
X[i] = X[idx];
X[idx] = t;
System.out.println("Pass : " + (i + 1));
for(int k = 0; k < n; k++) {
System.out.print(X[k] + " ");
}
System.out.println();
}
System.out.println("Sorted Array:");
for (int i = 0; i < n; i++) {
System.out.print(X[i] + " ");
}
}
}Output
Question 49
For the same array mentioned above in previous question, write a program to sort the above array using bubble sort technique. Give the array-status after every iteration.
public class KboatBubbleSort
{
public static void main(String args[]) {
int X[] = {13, 7, 6, 21, 35, 2, 28, 64, 45, 3, 5, 1};
int n = X.length;
//Bubble Sort
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (X[j] > X[j + 1]) {
int t = X[j];
X[j] = X[j+1];
X[j+1] = t;
}
}
System.out.println("Pass :" + (i + 1));
for(int k = 0; k < n; k++) {
System.out.print(X[k] + " ");
}
System.out.println();
}
System.out.println("Sorted Array:");
for (int i = 0; i < n; i++) {
System.out.print(X[i] + " ");
}
}
}Output

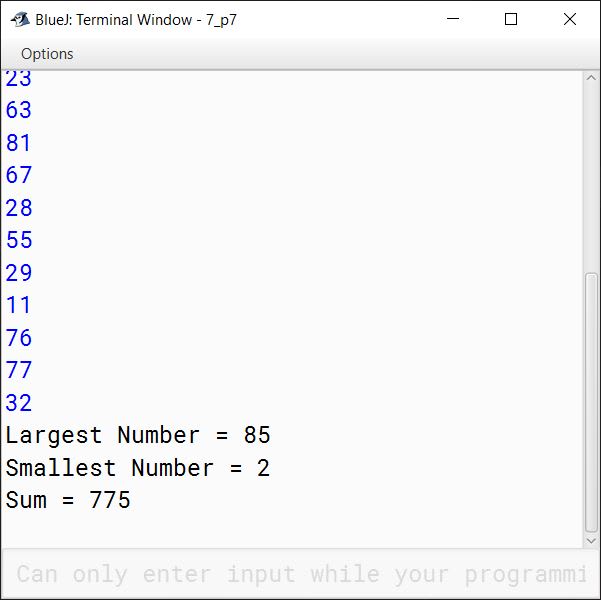
Question 50
Write a program to input integer elements into an array of size 20 and perform the following operations :
(i) Display largest number from the array.
(ii) Display smallest number from the array.
(iii) Display sum of all the elements of the array.
import java.util.Scanner;
public class KboatSDAMinMaxSum
{
public static void main(String args[]) {
Scanner in = new Scanner(System.in);
int arr[] = new int[20];
System.out.println("Enter 20 numbers:");
for (int i = 0; i < 20; i++) {
arr[i] = in.nextInt();
}
int min = arr[0], max = arr[0], sum = 0;
for (int i = 0; i < arr.length; i++) {
if (arr[i] < min)
min = arr[i];
if (arr[i] > max)
max = arr[i];
sum += arr[i];
}
System.out.println("Largest Number = " + max);
System.out.println("Smallest Number = " + min);
System.out.println("Sum = " + sum);
}
}Output
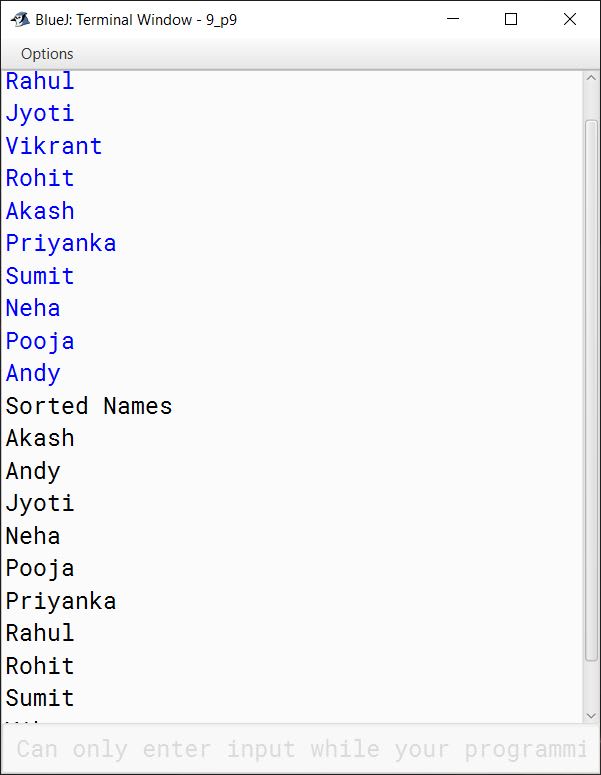
Question 51
Write a program to input forty words in an array. Arrange these words in descending order of alphabets, using selection sort technique. Print the sorted array.
import java.util.Scanner;
public class KboatSelectionSort
{
public static void main(String args[]) {
Scanner in = new Scanner(System.in);
String a[] = new String[40];
int n = a.length;
System.out.println("Enter 40 Names: ");
for (int i = 0; i < n; i++) {
a[i] = in.nextLine();
}
for (int i = 0; i < n - 1; i++) {
int idx = i;
for (int j = i + 1; j < n; j++) {
if (a[j].compareToIgnoreCase(a[idx]) < 0) {
idx = j;
}
}
String t = a[idx];
a[idx] = a[i];
a[i] = t;
}
System.out.println("Sorted Names");
for (int i = 0; i < n; i++) {
System.out.println(a[i]);
}
}
}Output
Question 52
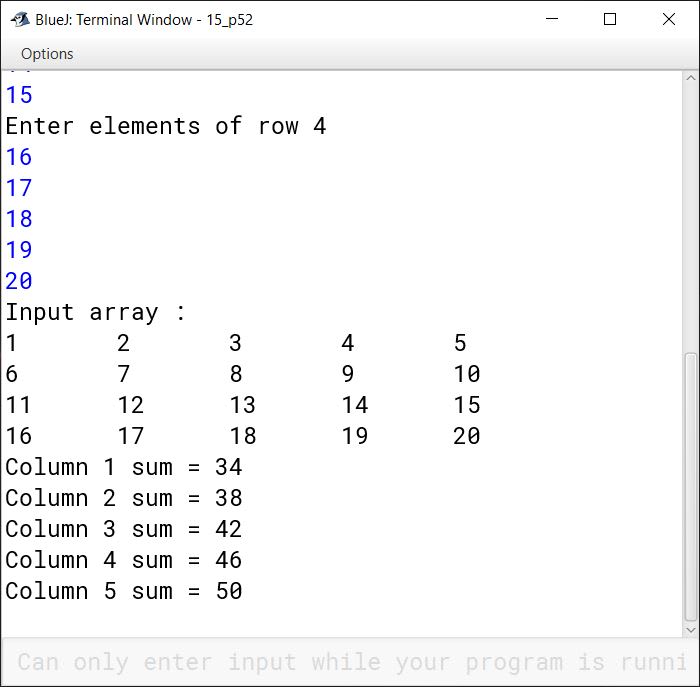
Write a program that reads a 4 x 5 two dimensional array and then prints the column sums of the array along with the array printed in matrix form.
import java.util.Scanner;
public class KboatDDAColSum
{
public static void main(String args[]) {
Scanner in = new Scanner(System.in);
int arr[][] = new int[4][5];
System.out.println("Enter the 2D array:");
for (int i = 0; i < 4; i++) {
System.out.println("Enter elements of row " + (i + 1));
for (int j = 0; j < 5; j++) {
arr[i][j] = in.nextInt();
}
}
System.out.println("Input array :");
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 5; j++) {
System.out.print(arr[i][j] + "\t");
}
System.out.println();
}
//Compute column-wise sum
for (int i = 0; i < 5; i++) {
int cSum = 0;
for (int j = 0; j < 4; j++) {
cSum += arr[j][i];
}
System.out.println("Column " + (i + 1)
+ " sum = " + cSum);
}
}
}Output
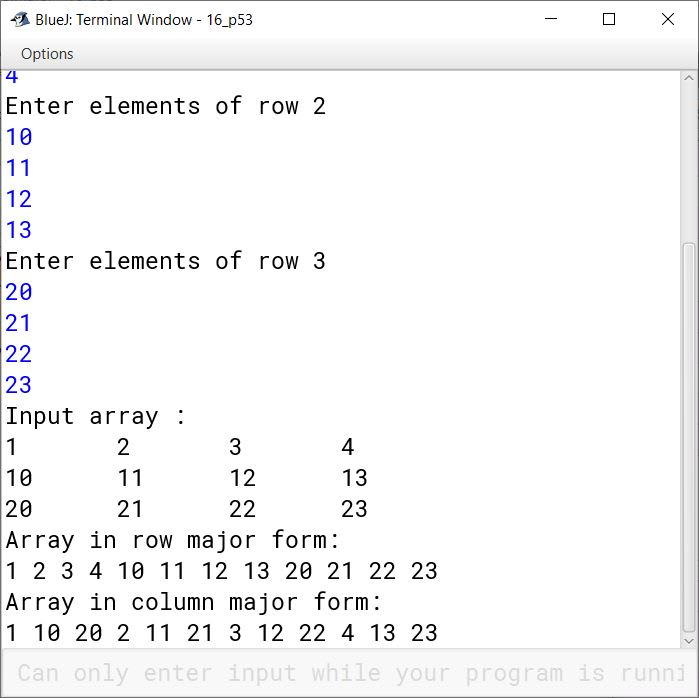
Question 53
Write a program that inputs a 2D array and displays how the array elements will look in row major form and column major form.
import java.util.Scanner;
public class KboatDDARowColMajor
{
public static void main(String args[]) {
Scanner in = new Scanner(System.in);
System.out.print("Enter number of rows: ");
int rows = in.nextInt();
System.out.print("Enter number of columns: ");
int cols = in.nextInt();
int arr[][] = new int[rows][cols];
System.out.println("Enter the 2D array:");
for (int i = 0; i < rows; i++) {
System.out.println("Enter elements of row " + (i + 1));
for (int j = 0; j < cols; j++) {
arr[i][j] = in.nextInt();
}
}
System.out.println("Input array :");
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
System.out.print(arr[i][j] + "\t");
}
System.out.println();
}
System.out.println("Array in row major form:");
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
System.out.print(arr[i][j] + " ");
}
}
System.out.println();
System.out.println("Array in column major form:");
for (int i = 0; i < cols; i++) {
for (int j = 0; j < rows; j++) {
System.out.print(arr[j][i] + " ");
}
}
}
}Output