Physical Quantities and Measurement

Objective Questions

Question 1

Write true or false for each statement:

(a) The S.I. unit of volume is litre.

(b) A measuring beaker of capacity 200 mL can measure only the volume of 200 mL of a liquid.

(c) cm² is a smaller unit of area than m².

(d) Equal volumes of two different substances have equal masses.

(e) The S.I. unit of density is g cm^-3.

(f) 1 g cm^-3 = 1000 kg m^-3.

(g) The density of water is maximum at 4°C.

(h) The speed 5 m s^-1 is less than 25 km h^-1.

(i) The S.I. unit of speed is m s^-1.

Answer

(a) False
Correct Statement — The S.I. unit of volume is cubic metre (m³).

(b) True

(c) True

(d) False
Correct Statement — Equal volumes of two different substances have different masses.

(e) False
Correct Statement — The S.I. unit of density is kg m^-3.

(f) True

(g) True

(h) True

(i) True

Question 2

Fill in the blanks:

(a) 1 m³ = ............... cm³

(b) The volume of an irregular solid is determined by the method of ............... .

(c) Volume of a cube = ............... .

(d) The area of an irregular lamina is measured by using a ............... .

(e) Mass = density x ............... .

(f) The S.I. unit of density is ............... .

(g) 1 g cm^-3 = ............... kg m^-3.

(h) 36 km h^-1 = ............... m s ^-1.

(i) Distance travelled D = ............... x time t.

Answer

(a) 10⁶

(b) displacement of liquid

(c) (one side)³

(d) graph paper

(e) volume

(f) kg m^-3

(g) 1000

(h) 10

(i) speed v

Question 3

Match the following:

Answer

Question 4a

Select the correct alternative:

One litre is equal to:

1. 1 cm³
2. 1 m³
3. 10^-3 cm³
4. 10^-3 m³

Answer

10^-3 m³

Reason — 1 litre = 10^-3 m³

Question 4b

Select the correct alternative:

A metallic piece displaces water of volume 15 mL. The volume of piece is:

1. 15 cm³
2. 15 m³
3. 15 x 10³ cm^-3
4. 15 x 10³ cm³

Answer

15 cm³

Reason — Volume of body is equal to volume of liquid displaced = 15 mL.
1 mL = 1 cm³, so 15 mL = 15 cm³.

Question 4c

Select the correct alternative:

A piece of paper of dimensions 1.5 m x 20 cm has area:

1. 30 m²
2. 300 cm²
3. 0.3 m²
4. 3000 m³

Answer

0.3 m²

Reason — 20 cm = 0.2 m
Area of paper = 1.5 m x 0.2 m = 0.3 m²

Question 4d

Select the correct alternative:

The correct relation is:

1. d = M x V
2. M = d x V
3. V = d x M
4. d = M + V

Answer

M = d x V

Reason — Mass = Volume x density

Question 4e

Select the correct alternative:

The density of alcohol is 0.8 g cm^-3. In S.I. unit, it will be:

1. 0.8 kg m^-3
2. 0.0008 kg m^-3
3. 800 kg m^-3
4. 8 x 10³ kg m^-3

Answer

800 kg m^-3

Reason — 1 g cm^-3 = 1000 kg m^-3
So 0.8 g cm^-3 = 800 kg m^-3

Question 4f

Select the correct alternative:

The density of aluminium is 2.7 g cm^-3 and of brass is 8.4 g cm^-3. For the same mass, the volume of:

1. both will be same
2. aluminium will be less than that of brass
3. aluminium will be more than that of brass
4. nothing can be said

Answer

aluminium will be more than that of brass

Reason — For a given mass of a substance, volume is inversely proportional to density. As density of aluminium is less than that of brass, so volume of aluminium will be more than that of brass.

Question 4g

Select the correct alternative:

A block of wood of density 0.8 g cm^-3 has a volume of 60 cm³. The mass of block will be:

1. 60.8 g
2. 75 g
3. 48 g
4. 0.013 g

Answer

48 g

Reason — Mass = density x volume
= 0.8 x 60
= 48 g
So, mass of block is 48 g.

Question 4h

Select the correct alternative:

The correct relation for speed is:

1. Speed = distance x time

2. Speed = $\dfrac{\text{distance}}{\text{time}}$

3. Speed = $\dfrac{\text{time}}{\text{distance}}$

4. Speed = $\dfrac{\text{1}}{\text{distance x time}}$

Answer

Speed = $\dfrac{\text{distance}}{\text{time}}$

Reason — Speed of a body = $\dfrac{\text{distance travelled by the body}}{\text{time of travel}}$

Question 4i

Select the correct alternative:

A boy travels a distance 150 m in 1 minute. His speed is:

1. 150 m s^-1
2. 2.5 m s^-1
3. 25 m s^-1
4. 9 m s^-1

Answer

2.5 m s^-1

Reason — time = 1 min = 60 sec, distance = 150 m $\text{Speed} = \dfrac{\text{distance}}{\text{time}} \\[1em] \text{Speed} = \dfrac{\text{150}}{\text{60}}$ Speed = 2.5 m s^-1

Short/Long Answer Questions

Question 1

Define the term volume of an object.

Answer

The space occupied by an object is called its volume.

Question 2

State and define the S.I. unit of volume.

Answer

The S.I. unit of volume is cubic metre (m³). One cubic metre is the volume of a cube with each side 1 metre long.

Question 3

State two smaller units of volume. How are they related to the S.I. unit?

Answer

The two smaller units of volume are cubic centimetre (cm³), cubic decimetre (dm³).

1 m³ = 1 m x 1 m x 1 m
= 100 cm x 100 cm x 100 cm
= 1000000 cm³
= 10⁶ cm³

So, 1 m³ = 10⁶ cm³

1 m³ = 1 m x 1 m x 1 m
= 10 dm x 10 dm x 10 dm
= 1000 dm³
= 10³ dm³

So, 1 m³ = 10³ dm³

Question 4

How will you determine the volume of a cuboid? Write the formula you will use.

Answer

The volume of a cuboid is determined by finding its three dimensions i.e., length, breadth and height.

The formula for volume of cuboid is length x breadth x height

Question 5

Name two devices which are used to measure the volume of an object. Draw their neat diagrams.

Answer

The two devices which are used to measure the volume of an object are:

1. Measuring cylinder

2. Measuring beaker

Question 6

How can you determine the volume of an irregular solid (say a piece of brass)? Describe in steps with neat diagrams.

Answer

The volume of an irregular solid can be measured by using a measuring cylinder by the method of displacement of liquid.

1. Place a measuring cylinder on a flat horizontal surface.
2. Fill it partially with water.
3. Note the reading of water level very carefully. Let it be V₁.
4. Now tie the piece of brass with a thread and dip it completely into water.
5. The level of water rises. Note the reading of new water level V₂. The difference in the two levels of water gives the volume of the piece of brass.

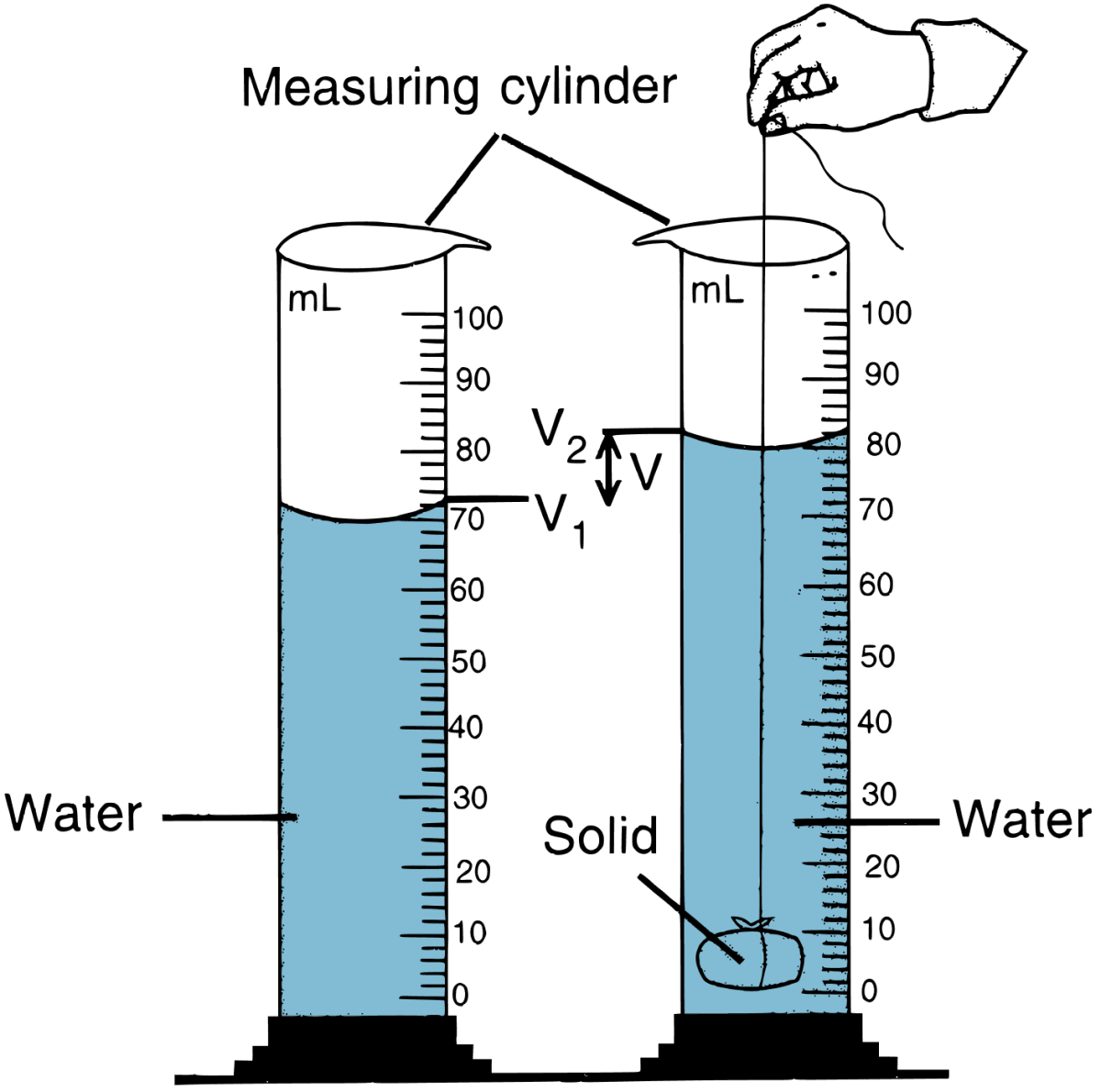
Question 7

You are required to take out 200 mL of milk from a bucket full of milk. How will you do it?

Answer

A measuring beaker of 200 mL is used to measure 200 mL of milk from a bucket full of milk.

1. Take a measuring beaker of 200 mL, wash and dry it.
2. Immerse the beaker inside the bucket full of milk.
3. Fill the beaker completely with the milk.
4. Take out the beaker from bucket gently so that no milk splashes out.
5. Pour the milk from measuring beaker into another empty vessel.

Question 8

Describe the method in steps to find the area of an irregular lamina using a graph paper.

Answer

To find the area of an irregular lamina using a graph paper.

1. Place the lamina over a graph paper.
2. Draw its boundary line on the graph paper with a pencil.
3. Remove the lamina.
4. Count and note the number of complete squares, half squares and more than half squares within the boundary line. Ignore the squares which are less than half.

The sum of the areas of the number of complete squares and the number of incomplete squares gives the approximate area of the irregular object.

Question 9

Define the term density of a substance.

Answer

The density of a substance is defined as the mass of a unit volume of that substance.

Question 10

State the S.I. and C.G.S. units of density. How are they related?

Answer

The S.I. unit of density is kg m^-3 and its C.G.S. unit is g cm^-3.

1 g cm^-3 = 1000 kg m^-3.

Question 11

The density of brass is 8.4 g cm^-3. What do you mean by the statement?

Answer

The statement means one cubic centimeter volume of brass has mass of 8.4 g.

Question 12

Arrange the following substances in order of their increasing density:

1. iron
2. cork
3. brass
4. water
5. mercury

Answer

Cork < Water < Iron < Brass < Mercury.

Question 13

How does the density of water change when:

(a) it is heated from 0°C to 4°C,

(b) it is heated from 4°C to 10°C ?

Answer

(a) Water when heated from 0°C to 4°C, it contracts so density of water increases and becomes maximum at 4°C.

(b) When water is heated from 4°C to 10°C it expands, so density decreases.

Question 14

Write the density of water at 4°C.

Answer

The density of water at 4°C is 1 g cm^-3 or 1000 kg m^-3.

Question 15

Explain the meaning of the term speed.

Answer

Speed of the body is distance travelled by the body in unit time. It tells us about the motion of the body i.e. how fast or slow it is moving.

Question 16

Write the S.I. unit of speed.

Answer

The S.I. unit of speed is metre per second (m s^-1).

Question 17

A car travels with a speed 12 m s^-1, while a scooter travels with a speed 36 km h^-1. Which of the two travels faster?

Answer

Speed of car = 12 m s^-1

Speed of scooter = 36 km h^-1

1 km h^-1 = $\dfrac{\text{5}}{\text{18}}$ m s^-1

36 km h^-1 = 36 x $\dfrac{\text{5}}{\text{18}}$ = 10 m s^-1

So speed of scooter = 10 m s^-1

So car travels faster than scooter; since speed of car is more than that of scooter.

Numericals

Question 1

The length, breadth and height of a water tank are 5 m, 2.5 m and 1.25 m respectively. Calculate the capacity of the water tank in:

a. m³

b. litre

Answer

Length = 5 m; breadth = 2.5 m; height = 1.25 m

a. Volume of water tank = length x breadth x height = 5 m x 2.5 m x 1.25 m = 15.625 m³

So, capacity of water tank in m³ = 15.625 m³.

b. 1 m³ = 1000 L
15.625 m³ = 15.625 x 1000 = 15625 L

So, capacity of water tank in litres = 15,625 L.

Question 2

A solid silver piece is immersed in water contained in a measuring cylinder. The level of water rises from 50 mL to 62 mL. Find the volume of silver piece.

Answer

Initial level of water V₁ = 50 mL
Final level of water V₂ = 62 mL

Volume of silver piece = V₂ - V₁
= 62 - 50
= 12 mL = 12 cm³

So, volume of silver piece = 12 cm³.

Question 3

Find the volume of a liquid present in a dish of dimensions 10 cm x 10 cm x 5 cm.

Answer

Volume of dish = 10 cm x 10 cm x 5 cm = 500 cm³.

Volume of liquid is equal to volume of dish = 500 cm³.

1 cm³ = 1 mL
500 cm³ = 500 mL

So, volume of a liquid present in the dish = 500 mL.

Question 4

A rectangular field is of length 60 m and breadth 35 m. Find the area of the field.

Answer

Length = 60 m
Breadth = 35 m

Area of the field = Length x Breadth = 60 m x 35 m = 2100 m².

So, area of the field = 2100 m².

Question 5

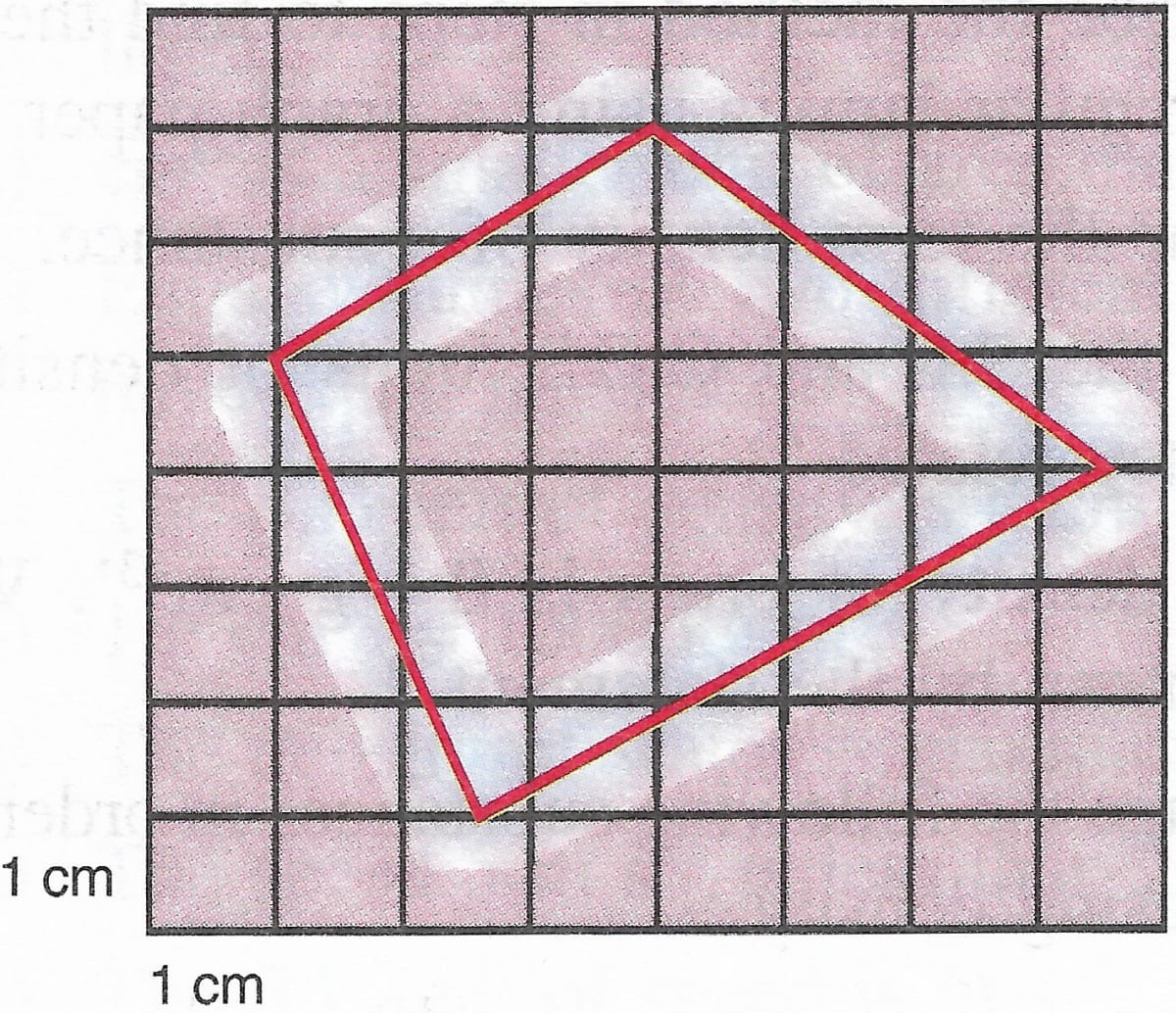
Find the approximate area of an irregular lamina of which boundary line is drawn on the graph paper shown in figure below.

Answer

Number of complete squares = 11
Number of more than half squares = 8
Number of half squares = 2
Total number of squares = 11 + 8 + 2 = 21
Area of the square = 1 cm x 1 cm = 1 cm²
Area of 21 squares = 21 x 1 = 21 cm²

So, approximate area of lamina = 21 cm².

Question 6

A piece of brass of volume 30 cm³ has a mass of 252 g. Find the density of brass in:

(i) g cm^-3

(ii) kg m^-3

Answer

Mass = 252 g
Volume = 30 cm^-3
Density = ?

(i) $\text{Density} = \dfrac{\text{Mass}}{\text{Volume}} \\[1em] \text{Density} = \dfrac{\text{252}}{\text{30}} = 8.4 \text{g cm}^{-3}$

So, Density = 8.4 g cm^-3.

(ii) 1 g cm^-3 = 1000 kg m^-3
8.4 g cm^-3 = 8.4 x 1000 = 8400 kg m^-3

So, Density = 8400 kg m^-3.

Question 7

The mass of an iron ball is 312 g. The density of iron is 7.8 g cm^-3. Find the volume of the ball.

Answer

Mass = 312 g
Density = 7.8 g cm^-3
Volume = ?

$\text{Density} = \dfrac{\text{Mass}}{\text{Volume}} \\[1em] \text{7.8} = \dfrac{\text{312}}{\text{Volume}} \\[1em] \text{Volume} = \dfrac{\text{312}}{\text{7.8}} = 40 \text{cm}^{3}$

So, volume of the ball is 40 cm³.

Question 8

A cork has a volume 25 cm³. The density of cork is 0.25 g cm^-3. Find the mass of the cork.

Answer

Volume = 25 cm³
Density = 0.25 g cm^-3
Mass = ?

$\text{Density} = \dfrac{\text{Mass}}{\text{Volume}} \\[1em] \text{0.25} = \dfrac{\text{Mass}}{\text{25}} \\[1em] \text{Mass} = 0.25 \times 25 = 6.25 \text{g}$

So, mass of the cork is 6.25 g.

Question 9

The mass of 5 litre of water is 5 kg. Find the density of water in g cm^-3.

Answer

Mass = 5 kg
Volume = 5 litre
Density = ?

$\text{Density} = \dfrac{\text{Mass}}{\text{Volume}} \\[1em] \text{Density} = \dfrac{\text{5}}{\text{5}} = 1 \text{kg litre}^{-1}$

Density = 1 kg litre^-1

1 kg = 1000 g; 1 litre = 1000 cm³

1 kg litre^-1 = $\dfrac{\text{1000}}{\text{1000}}$ = 1 g cm^-3

So, density of water = 1 g cm^-3.

Question 10

A cubical tank of side 1 m is filled with 800 kg of a liquid. Find:

(i) the volume of tank

(ii) the density of liquid in kg m^-3.

Answer

Side = 1 m; mass = 800 kg

(i) Volume of cubical tank = (side)³ = (1 m)³ = 1 m³

So, volume of tank = 1 m³.

(ii) $\text{Density} = \dfrac{\text{Mass}}{\text{Volume}} \\[1em] \text{Density} = \dfrac{\text{800}}{\text{1}} = 800 \text{kg m}^{3}$

So, density of liquid = 800 kg m^-3.

Question 11

A block of iron has dimensions 2 m x 0.5 m x 0.25 m. The density of iron is 7.8 g cm^-3. Find the mass of the block.

Answer

Density of iron = 7.8 g cm^-3
1 g cm^-3 = 1000 kg m^-3
7.8 g cm^-3 = 7.8 x 1000 = 7800 kg m^-3

Volume of iron = 2 m x 0.5 m x 0.25 m = 0.25 m³

Mass = ?

$\text{Density} = \dfrac{\text{Mass}}{\text{Volume}} \\[1em] \text{7800} = \dfrac{\text{Mass}}{\text{0.25}} \\[1em] \text{Mass} = 7800 \times 0.25 = 1950 \text{kg}$

So, mass of iron = 1950 kg.

Question 12

The mass of a lead piece is 115 g. When it is immersed into a measuring cylinder, the water level rises from 20 mL mark to 30 mL mark. Find:

(i) the volume of the lead piece,

(ii) the density of the lead in kg m^-3.

Answer

(i) Mass = 115 g;
Initial volume V₁ = 20 mL;
Final volume V₂ = 30 mL;
Volume of lead piece = V₂ - V₁ = 30 - 20 = 10 mL

1 mL = 1 cm³
10 mL = 10 cm³

So, volume of the lead piece = 10 cm³.

(ii) Density = ? $\text{Density} = \dfrac{\text{Mass}}{\text{Volume}} \\[1em] \text{Density} = \dfrac{\text{115}}{\text{10}} = 11.5 \text{g cm}^{3}$

1 g cm^-3 = 1000 kg m^-3
11.5 g cm^-3 = 1000 x 11.5 = 11500 kg m^-3

So, density of lead = 11500 kg m^-3.

Question 13

The density of copper is 8.9 g cm^-3. What will be its density in kg m^-3?

Answer

1 g cm^-3 = 1000 kg m^-3
8.9 g cm^-3 = 8.9 x 1000 = 8900 kg m^-3

So, density of copper = 8900 kg m^-3.

Question 14

A car travels a distance of 15 km in 20 minute. Find the speed of the car in:

(i) km h^-1

(ii) m s^-1

Answer

(i) distance = 15 km; time = 20 min

60 min = 1 hr

20 min = $\dfrac{\text{20}}{\text{60}}$ = $\dfrac{\text{1}}{\text{3}}$ h

$\text{Speed} = \dfrac{\text{distance}}{\text{time}} \\[1em] = \dfrac{15}{\dfrac{1}{3}} \\[1em] = 15 \times 3 \\[1em] = 45 \text{km h}^{-1}$ So, speed of car = 45 km h^-1.

(ii) distance = 15 km
1 km = 1000 m
15 km = 15 x 1000 = 15000 m

time = 20 min
1 min = 60 sec
20 min = 20 x 60 = 1200 sec

$\text{Speed} = \dfrac{\text{distance}}{\text{time}} \\[1em] = \dfrac{\text{15000}}{\text{1200}} = 12.5 \text{ m s}^{-1}$

So, speed of car = 12.5 m s^-1.

Question 15

How long a train will take to travel a distance of 200 km with a speed of 60 km h^-1?

Answer

distance = 200 km; speed = 60 km h^-1

time = ?

$\text{Speed} = \dfrac{\text{distance}}{\text{time}} \\[1em] \text{60} = \dfrac{\text{200}}{\text{time}} \\[1em] \text{time} = \dfrac{\text{200}}{\text{60}} = 3\text{h } 20\text{min}$

So, time taken by train will be 3 hrs 20 minutes.

Question 16

A boy travels with a speed of 10 m s^-1 for 30 minute. How much distance does he travel?

Answer

Speed = 10 m s^-1
time = 30 minutes
1 min = 60 sec
30 min = 60 x 30 = 1800 sec

distance = ?

$\text{Speed} = \dfrac{\text{distance}}{\text{time}} \\[1em] \text{10} = \dfrac{\text{distance}}{\text{1800}} \\[1em] \text{distance} = 1800 \times 10 = 18000 \text{ m}$

So, distance travelled = 18000 m or 18 km.

Question 17

Express 36 km h^-1 in m s^-1.

Answer

1 km h^-1 = $\dfrac{\text{5}}{\text{18}}$ m s^-1

36 km h^-1 = 36 x $\dfrac{\text{5}}{\text{18}}$ = 10 m s^-1

So, 36 km h^-1 = 10 m s^-1.

Question 18

Express 15 m s^-1 in km h^-1.

Answer

1 m s^-1 = 3.6 km h^-1

15 m s^-1 = 3.6 x 15 = 54 km h^-1

So, 15 m s^-1 = 54 km h^-1.