Objective Questions
Question 1
Write true or false for each statement:
(a) Equal volumes of two different substances have equal masses.
(b) The density of a piece of brass will change by changing its size or shape.
(c) The density of a liquid decreases with increase in its temperature.
(d) Relative density of water is 1.0.
(e) Relative density of a substance is expressed in g cm-3.
(f) When a body is immersed in a liquid, the buoyant force experienced by the body is equal to the volume of the liquid displaced by it.
(g) A body experiences the same buoyant force while floating in water or alcohol.
(h) A body experiences the same buoyant force when it floats or sinks in water.
(i) A body floats in a liquid when its weight becomes equal to the weight of the liquid displaced by its submerged part.
(j) A body while floating, sinks deeper in a liquid of low density than in a liquid of high density.
Answer
(a) False
Correct Statement — Equal volumes of two different substances have different masses.
(b) False
Correct Statement — The density of a piece of brass will not change by changing its size or shape.
(c) True
(d) True
(e) False
Correct Statement — Relative density has no unit.
(f) False
Correct Statement — When a body is immersed in a liquid, the buoyant force experienced by the body is equal to the weight of the liquid displaced by the immersed part of the body.
(g) True
(h) False
Correct Statement — The buoyant force experience by the body is different when floating or sinking in water.
(i) True
(j) True
Question 2
Fill in the blanks:
(a) 1 kg is the mass of ............... mL of water at 4°C.
(b) Mass = density x ............... .
(c) The S.I. unit of density is ............... .
(d) Density of water is ............... kg m-3.
(e) 1 g cm-3 = ............... kg m-3.
(f) The density of a body which sinks in water is ............... than 1000 kg m-3.
(g) A body sinks in a liquid A, but floats in a liquid B. The density of liquid A is ............... than the density of liquid B.
(h) A body X sinks in water, but a body Y floats on water. The density of the body X is ............... than the density of body Y.
(i) The buoyant force experienced by a body when floating in salt-water is ............... that when floating in pure water.
(j) The weight of a body floating in a liquid is ............... .
Answer
(a) 1000
(b) volume
(c) kg m-3
(d) 1000
(e) 1000
(f) more
(g) less
(h) more
(i) equal to
(j) zero
Question 3
Match the following:
| Column A | Column B |
|---|---|
| (a) kg m-3 | (i) relative density |
| (b) No unit | (ii) sinks in alcohol |
| (c) Relative density | (iii) floats on water |
| (d) Iron | (iv) density |
| (e) Wood | (v) density bottle |
Answer
| Column A | Column B |
|---|---|
| (a) kg m-3 | (iv) density |
| (b) No unit | (i) relative density |
| (c) Relative density | (v) density bottle |
| (d) Iron | (ii) sinks in alcohol |
| (e) Wood | (iii) floats on water |
Question 4a
Select the correct alternative:
The correct relation is:
- Density = Mass x Volume
- Mass = Density x Volume
- Volume = Density x Mass
- Density = Mass + Volume
Answer
Mass = Density x Volume
Reason — The density of a substance is its mass per unit volume.
Question 4b
Select the correct alternative:
The relative density of alcohol is 0.8. Its density is:
- 0.8
- 800 kg m-3
- 800 g cm-3
- 0.8 kg m-3
Answer
800 kg m-3
Reason —
Question 4c
Select the correct alternative:
A block of wood of density 0.8 g cm-3 has a volume of 60 cm-3. The mass of block is:
- 60.8 g
- 75 g
- 48 g
- 0.013 g
Answer
48 g
Reason —
Question 4d
Select the correct alternative:
The density of aluminium is 2.7 g cm-3 and that of brass is 8.4 g cm-3. The correct statement is:
- Equal masses of aluminium and brass have equal volumes.
- The mass of a certain volume of brass is more than the mass of equal volume of aluminium.
- The volume of a certain mass of brass is more than the volume of equal mass of aluminium.
- Equal volumes of aluminium and brass have equal masses.
Answer
The mass of a certain volume of brass is more than the mass of equal volume of aluminium.
Reason —
So mass of certain volume of brass will be more than the mass of same volume of aluminium as density of brass is more than density of aluminium.
Question 4e
Select the correct alternative:
A density bottle has a marking 25 mL on it. It means that:
- the mass of density bottle is 25 g.
- the density bottle will store 25 mL of any liquid in it.
- the density bottle will store 25 mL of water, but more volume of liquid denser than water.
- the density bottle will store 25 mL of water, but more volume of a liquid lighter than water.
Answer
The density bottle will store 25 mL of any liquid in it.
Reason — A density bottle can store specific volume of any density of liquid. Since this bottle is marked 25 mL so it can store 25 mL of any density liquid in it.
Question 4f
Select the correct alternative:
The correct statement is:
- The buoyant force on a body is equal to the volume of the liquid displaced by it.
- The buoyant force on a body is equal to the volume of the body.
- The buoyant force on a body is equal to the weight of the liquid displaced by it.
- The buoyant force on a body is always equal to the weight of the body.
Answer
The buoyant force on a body is equal to the weight of the liquid displaced by it.
Reason — According to Principle of Floatation, the buoyant force is equal to the weight of the liquid displaced by the immersed part of the body.
Question 4g
Select the correct alternative:
A piece of wood floats on water. The buoyant force on wood will be:
- zero
- more than the weight of the wood piece.
- equal to the weight of the wood piece.
- less than the weight of the wood piece.
Answer
equal to the weight of the wood piece
Reason — According to Law of Floatation when a body floats on water the weight of the body is equal to the buoyant force.
Question 4h
Select the correct alternative:
The weight of a body is more than the buoyant force experienced by it, due to a liquid. The body will:
- sink
- float with its some part outside the liquid.
- float just below the surface of liquid.
- float with whole of its volume above the surface of liquid.
Answer
sink
Reason — According to the Principle of Floatation, if the weight of the body is more than the buoyant force acting on the body the body will sink into the liquid.
Short/Long Answer Questions
Question 1
Define the term density of a substance.
Answer
The density of a substance is its mass per unit volume i.e.
Question 2
Name the S.I. unit of density. How is it related to g cm-3.
Answer
The S.I. unit of density is kg m-3 (kilogram per cubic metre).
1 g cm-3 = 1000 kg m-3.
Question 3
The density of brass is 8.4 g cm-3. What do you mean by this statement?
Answer
The statement means one cubic centimeter volume of brass has mass of 8.4 g.
Question 4
Arrange the following substances in order of their increasing density:
Iron, Cork, Brass, Water, Mercury.
Answer
Cork < Water < Iron < Brass < Mercury.
The density of cork is the least and that of mercury is the most.
Question 5
How does the density of a liquid (or gas) vary with temperature?
Answer
When temperature increases, volume of most of the liquid increases, so density decreases. Similarly when temperature decreases volume of liquids decreases so density increases. But exception is water which contracts on heating from 0°C to 4°C and expands on heating above 4°C. Water has maximum density at 4 degree celsius.
Question 6
A given quantity of a liquid is heated. Which of the following quantity will vary and how?
(a) mass
(b) volume
(c) density
Answer
(a) Mass of the liquid remains unaffected on heating.
(b) Volume of the liquid increases with increase in temperature.
(c) Density of liquid decreases on heating because its volume increases and density is inversely proportional to volume.
Question 7
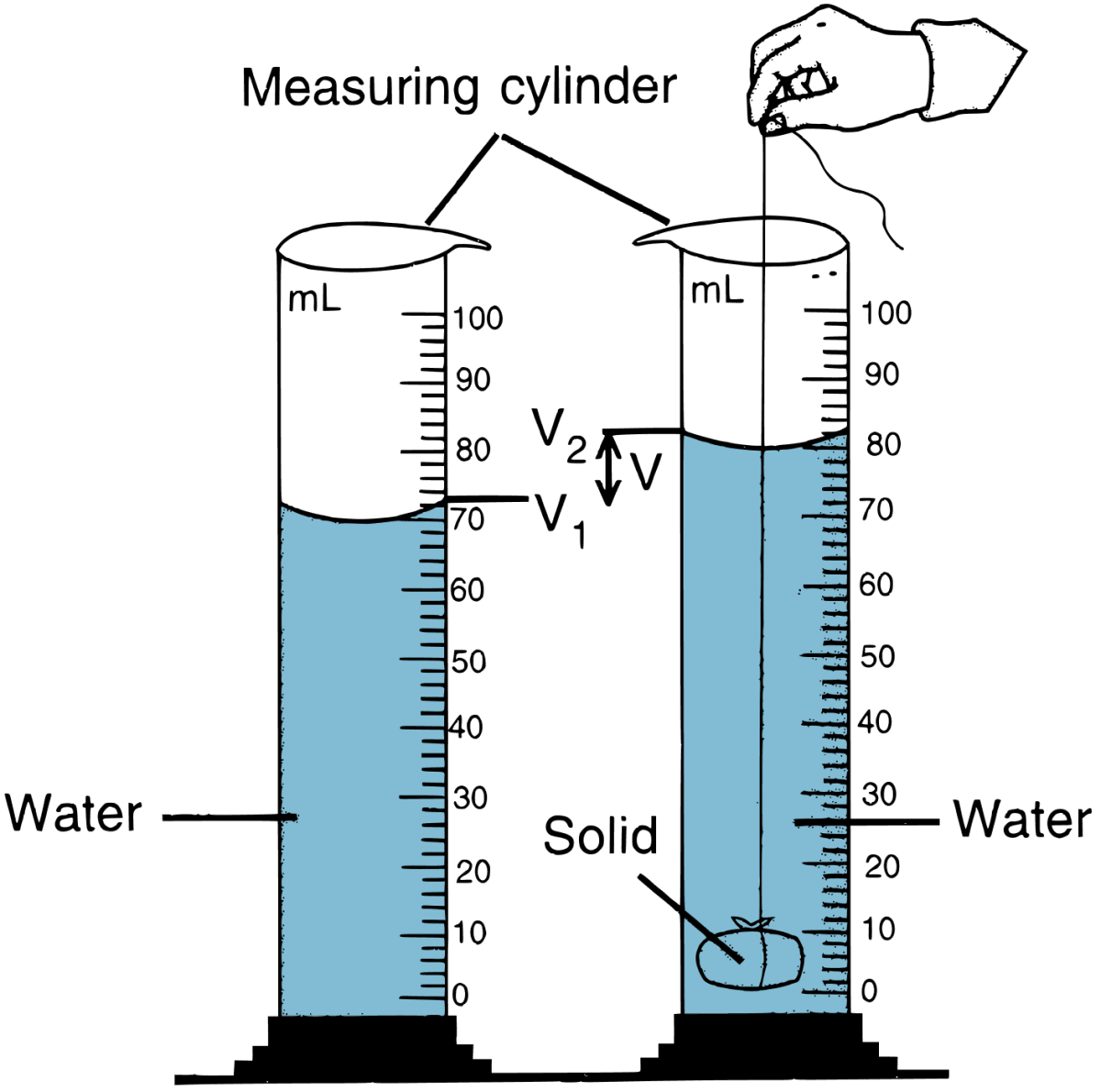
Describe an experiment to determine the density of the material of a coin.
Answer
The density of the material of a coin is determined by the following experiment:
- We know density is mass per unit volume. So, first mass of the coin is measured by a common beam balance. Let it be M gram.
- Volume of the coin is measured by a measuring cylinder as shown in the figure given below.
- Take a measuring cylinder and fill it partly with water.
- Note the level of water. Let it be V1 mL.
- Tie the coin with a thread and gently lower the coin inside the measuring cylinder. Take care that no water splashes out.
- Note the level of water again. Let it be V2 mL.
- Find the volume of the coin (V) by subtracting V1 from V2.
V = V2 - V1
Density of coin is calculated by the formula:
Question 8
Describe an experiment to determine the density of a liquid.
Answer
The density of a liquid is determined by first finding its mass and then its volume.
- Take an empty beaker and measure its mass by using a common beam balance. Let the mass be M1 g.
- Take some amount of liquid and pour it into the empty beaker. Measure its mass again. Let it be M2 g.
- The difference between M2 and M1 gives the mass(M) of the liquid. M = M2 - M1.
- Pour the liquid from beaker into a measuring cylinder. Note the volume of the liquid. Let it be V mL or V g cm-3.
- Calculate the density of the liquid using the following formula:
Question 9
What is a density bottle? How is it used to find the density of a liquid?
Answer
A density bottle is a specially designed bottle which is used to determine the density of a liquid. The figure of density bottle is shown below:

Determination of Density of a Liquid using the Density Bottle
- Measure the mass of empty density bottle using a beam balance. Let it be M1 g.
- Remove the stopper of the bottle and fill it with water. Replace the stopper, wipe the outside of bottle dry and measure its mass again. Let it be M2 g.
- Empty the bottle and dry it. Fill it with the given liquid, replace the stopper and wipe the outside of bottle dry. Measure its mass. Let it be M3 g.
- Calculate the mass of water (M2 - M1) and the mass of liquid (M3 - M1).
- Since density of water is 1 g cm-3, mass of water contained in bottle is the volume of bottle. Thus,
Mass of liquid = M3 - M1
Volume of liquid = M2 - M1
Question 10
Define the term relative density of a substance.
Answer
The relative density of a substance is defined as the ratio of the density of a substance to the density of water. The symbol used for relative density is R.D. Thus,
Question 11
What is the unit of relative density?
Answer
Relative density has no unit because it is the ratio of two densities.
Question 12
Distinguish between density and relative density.
Answer
| Sl. No. | Density | Relative Density |
|---|---|---|
| (i) | Density of a substance is defined as the mass of a unit volume of that substance. | The relative density of a substance is defined as the ratio of the density of a substance to the density of water. |
| (ii) | Units are kg m-3, g cm-3. | Relative Density has no units. |
Question 13
Explain the meaning of the statement 'Relative density of aluminium is 2.7'.
Answer
Relative density of aluminium is 2.7 means a piece of aluminium of any volume has mass 2.7 times that of an equal volume of water.
Question 14
How does the density of a body and that of a liquid determine whether the body will float or sink into that liquid?
Answer
If the density of a body is less than the density of liquid, the body will float on the surface of the liquid. But if the density of a body is more than the density of liquid the body will sink in the liquid.
Question 15
A cork piece floats on water surface while an iron nail sinks in it. Explain the reason.
Answer
The density of cork is less than the density of water so it floats on water surface but the density of iron nail is more than the density of water so it sinks in water.
Question 16
Which of the following will sink or float on water? (Density of water = 1 g cm-3)
- Body A having density 500 kg m-3
- Body B having density 2520 kg m-3
- Body C having density 1100 kg m-3
- Body D having density 0.85 g cm-3
Answer
- Body A will float on water because its density (500 kg m-3) is less than the density of water (1 g cm-3 or 1000 kg m-3).
- Body B will sink in water because its density (2520 kg m-3) is more than the density of water (1 g cm-3 or 1000 kg m-3).
- Body C will sink in water because its density (1100 kg m-3) is more than the density of water (1 g cm-3 or 1000 kg m-3).
- Body D will float on water because its density (0.85 g cm-3) is less than the density of water (1 g cm-3).
Question 17
State the law of floatation?
Answer
The law of floatation states that — "When a body floats in a liquid, the weight of the liquid displaced by its immersed part is equal to the total weight of the body".
i.e., while floating
Weight of the floating body = Weight of the liquid displaced by its immersed part (i.e., buoyant force)
Question 18
The density of water is 1.0 g cm-3. The density of iron is 7.8 g cm-3. The density of mercury is 13.6 g cm-3. Answer the following:
(a) Will a piece of iron float or sink in water?
(b) Will a piece of iron float or sink in mercury?
Answer
(a) Iron will sink in water as density of iron (7.8 g cm-3) is more than the density of water (1 g cm-3).
(b) Iron will float in mercury as the density of iron (7.8 g cm-3) is less than the density of mercury (13.6 g cm-3).
Question 19
The diagram given below shows a body floating in three different liquids A, B and C at different levels.
(a) In which liquid does the body experience the greatest buoyant force?
(b) Which liquid has the least density?
(c) Which liquid has the highest density?

Answer
(a) The buoyant force is same in each case as the weight of the body is same in each case and the buoyant force is equal to the weight of the liquid displaced by the immersed part of the body which balances the weight of the body.
(b) Liquid A has the least density as the maximum part of the body is immersed in liquid A.
(c) Liquid C has the highest density as the body immerses the least in liquid C.
Question 20
For a floating body, how is its weight related to the buoyant force?
Answer
When a body floats in a liquid, the weight of the liquid displaced by its immersed part (i.e. the buoyant force) is equal to the total weight of the body.
Question 21
Why does a piece of ice float on water?
Answer
Density of ice is 0.9 g cm-3 and density of water is 1.0 g cm-3. Since density of ice is less than density of water, so ice floats on water.
Question 22
Explain why an iron needle sinks in water, but a ship made of iron floats on water.
Answer
An iron needle is solid and density of iron is more than that of water. Weight of iron needle is more than the buoyant force of water on it so it sinks in water. Although ship is made of iron but it has hollow space that is filled with air which make its average density less than that of water, so ship floats on water.
Question 23
It is easier to swim in sea water than in river water. Explain the reason.
Answer
Sea water contains salts so its density is more than the density of river water. The weight of a person gets balanced by the less immersed part of his body in sea water as compared to that in river water. Thus, it is easier to swim in sea water than in river water.
Question 24
Icebergs floating on sea water are dangerous for ships. Explain the reason.
Answer
Density of ice (0.9 g cm-3) is less than the density of sea water (1.02 g cm-3). So, an iceberg floats in sea water with its large portion submerged inside the water and only a little portion of it is above the surface of water. Thus, a ship can collide with the invisible part of the iceberg under the surface of water. Hence, it is dangerous.
Question 25
Explain why it is easier to lift a stone under water than in air.
Answer
When a stone is under water then its weight is less than its weight in air because it experiences an upward buoyant force. Due to apparent loss in weight, it is lighter in water which makes it easier to lift in water than in the air.
Question 26
What is a submarine? How can it be made to dive in water and come to the surface of water?
Answer
A submarine is a water tight boat which can travel under water like a ship and it is provided with water tanks.
To make the submarine dive, the tanks are filled with water so that the average density of the submarine becomes greater than the density of sea water, so it sinks into the water.
To make the submarine rise to the surface of water, these tanks are emptied. This makes the average density of the submarine less than the density of sea water, so the submarine rises up to the surface of water.
Question 27
A balloon filled with hydrogen rises in air. Explain the reason.
Answer
The density of hydrogen gas is less than the density of air. So the buoyant force experienced by the balloon due to air is greater than the weight of the balloon. Due to this net upward force balloon rises up in air.
Numericals
Question 1
The density of air is 1.28 g litre-1. Express it in:
(a) g cm-3
(b) kg m-3
Answer
(a) The density of air is 1.28 g litre-1.
1 litre = 1000 cm3
∴ Density of air in g cm-3 =
Density of air = 0.00128 g cm-3
(b) Density of air in kg m-3 = Density of air in g cm -3 x 1000 = 0.00128 x 1000 = 1.28 kg m-3
∴ Density of air in kg m-3 = 1.28 kg m-3.
Question 2
The dimensions of a hall are 10 m x 7 m x 5 m. If the density of air is 1.11 kg m-3, find the mass of air in the hall.
Answer
Density of air = 1.11 kg m-3
Volume of hall = 10 m x 7 m x 5 m = 350 m3
Mass = ?
We know,
Hence, the mass of air in the hall = 388.5 kg.
Question 3
The density of aluminium is 2.7 g cm-3. Express it in kg m-3.
Answer
Density of Aluminium = 2.7 g cm-3.
Density of aluminium in kg m-3 = 2.7 x 1000 = 2700 kg m-3
Hence, Density of aluminium = 2700 kg m-3.
Question 4
The density of alcohol is 600 kg m-3. Express it in g cm-3.
Answer
Hence, Density of Alcohol in g cm-3 = 0.6 g cm-3.
Question 5
A piece of zinc of mass 438.6 g has a volume of 86 cm3. Calculate the density of zinc.
Answer
Mass of zinc = 438.6 g
Volume of zinc = 86 cm3
Density of zinc = ?
So, Density of Zinc = 5.1 g cm-3.
Question 6
A piece of wood of mass 150 g has a volume of 200 cm3. Find the density of wood in
(a) C.G.S. unit
(b) S.I. unit
Answer
Mass of wood = 150 g
Volume of wood = 200 cm3
Density of wood = ?
(a) C.G.S. unit of density is g cm-3.
Density of wood = 0.75 g cm-3.
(b) S.I. unit of density is kg m-3.
Density of Wood in kg m-3 = Density of Wood in g cm-3 x 1000 = 0.75 x 1000 = 750 kg m-3
So, Density of Wood = 750 kg m-3.
Question 7
Calculate the volume of wood of mass 6000 kg if the density of wood is 0.8 g cm-3.
Answer
Density of wood = 0.8 g cm-3 or 800 kg m-3
Mass of wood = 6000 kg
Volume of wood = ?
So, Volume of wood = 7.5 m3.
Question 8
Calculate the density of a solid from the following data:
(a) Mass of solid = 72 g
(b) Initial volume of water in measuring cylinder = 24 mL
(c) Final volume of water when solid is completely immersed in water = 42 mL
Answer
Mass of solid = 72 g
Volume of solid = Final volume of water - Initial volume of water
Volume of solid = 42 - 24 = 18 mL
So, Density of solid = 4.0 g cm-3.
Question 9
The mass of an empty density bottle is 21.8 g, when filled completely with water it is 41.8 g and when filled completely with liquid it is 40.6 g. Find:
(a) the volume of density bottle.
(b) the relative density of liquid.
Answer
Mass of empty density bottle (M1) = 21.8 g
Mass of bottle with water (M2) = 41.8 g
Mass of bottle with liquid (M3)= 40.6 g
(a) Mass of water in bottle = M2 - M1 = 41.8 - 21.8 = 20 g
Density of water is 1 g cm-3, so volume of density bottle = 20 mL
(b) Mass of liquid in bottle = M3 - M1 = 40.6 - 21.8 = 18.8 g
Relative density of liquid = 0.94.
Question 10
From the following observations, calculate the density and relative density of a brine solution.
Mass of empty density bottle = 22 g
Mass of bottle + water = 50 g
Mass of bottle + brine solution = 54 g
Answer
Mass of empty density bottle (M1) = 22 g
Mass of bottle + water (M2) = 50 g
Mass of bottle + brine solution (M3) = 54 g
Mass of water in bottle = M2 - M1 = 50 - 22 = 28 g
Density of water is 1 g cm-3, so volume of density bottle = 28 cm3.
Mass of brine solution in bottle = M3 - M1 = 54 - 22 = 32 g
So, density of brine solution = 1.14 g cm-3.
So, Relative density of brine solution is 1.14.
Question 11
The mass of an empty density bottle is 30 g, it is 75 g when filled completely with water and 65 g when filled completely with a liquid. Find:
(a) Volume of density bottle,
(b) Density of liquid and
(c) Relative density of liquid.
Answer
Mass of empty density bottle (M1) = 30 g
Mass of bottle with water (M2) = 75 g
Mass of bottle with liquid (M3)= 65 g
(a) Mass of water in bottle = M2 - M1 = 75 - 30 = 45 g
Density of water is 1 g cm-3, so volume of density bottle = 45 mL.
(b) Mass of liquid in bottle = M3 - M1 = 65 - 30 = 35 g
So, density of liquid = 0.77 g cm-3.
(c)
So, Relative density of liquid is 0.77.