Solved 2020 Question Paper ICSE Class 10 Physics

Section I (40 Marks)

Question 1(a)

(i) Define moment of force. [2]

(ii) Write the relationship between the S.I. and C.G.S. unit of moment of force.

Answer

(i) The moment of force is equal to the product of the magnitude of the force and the perpendicular distance of the line of action of force from the axis of rotation.

(ii) The S.I. and C.G.S. unit of moment of force are related as follows —

1 N m = 10⁵ dyne x 10² cm = 10⁷dyne cm

Question 1(b)

Define a kilowatt hour. How is it related to joule? [2]

Answer

One kilowatt hour is the electrical energy consumed by an electrical appliance of power 1 kilowatt when it is used for 1 hour.

1 kilowatt hour = 1 kilowatt x 1 hour
= 1000 J s^-1 x 3600 s = 3.6 x 10⁶ J

Question 1(c)

A satellite revolves around a planet in a circular orbit. What is the work done by the satellite at any instant? Give a reason. [2]

Answer

The work done is zero because the centripetal force on the body at any instant is directed towards the centre of the circular path and the displacement at that instant is along the tangent to the circular path, i.e., normal to the direction of force on the body. Since, θ = 90° , cos 90° = 0. Therefore, work done is zero.

Question 1(d)

(i) Identify the class of the lever shown in the diagram below: [2]

(ii) How is it possible to increase the M.A. of the above lever without increasing it's length?

Answer

(i) The class of the lever shown in the diagram is class III.

(ii) By applying effort at a larger distance from the fulcrum i.e., shifting effort E towards load L, thereby increasing the length of effort arm.

Question 1(e)

Give one example of each when: [2]

(i) Chemical energy changes into electrical energy.

(ii) Electrical energy changes into sound energy.

Answer

(i) Chemical energy changes into electrical energy — In a battery when current is drawn from it in the external circuit.

(ii) Electrical energy changes into sound energy — In a loud speaker, electrical signals vibrate the diaphragm of loud speaker to produce sound.

Question 2(a)

A crane 'A' lifts a heavy load in 5 seconds, whereas another crane 'B' does the same work in 2 seconds. Compare the power of crane 'A' to that of crane 'B'. [2]

Answer

Let the work done by both cranes be 'W'

Given,

Time taken by crane A to do work, t₁ = 5 s

Time taken by crane B to do work, t₂ = 2 s

Power of crane A, P_A = $\dfrac{W}{t_1}$

Power of crane B, P_B = $\dfrac{W}{t_2}$

$\dfrac{P_A}{P_B} = \dfrac{Wt_2}{Wt_1} \\[0.5em] \dfrac{P_A}{P_B} = \dfrac{t_2}{t_1} \\[0.5em] \dfrac{P_A}{P_B} = \dfrac{2}{5}$

P_A : P_B = 2 : 5

Question 2(b)

A ray of light falls normally on a rectangular glass slab. Draw a ray diagram showing the path of the ray till it emerges out of the slab. [2]

Answer

Below is the ray diagram showing the path of the ray till it emerges out of the slab:

Question 2(c)

Complete the path of the monochromatic light ray AB incident on the surface PQ of the equilateral glass prism PQR till it emerges out of the prism due to refraction. [2]

Answer

Below ray diagram shows the path of ray AB till it emerges out of the prism:

Question 2(d)

Where should an object be placed in front of a convex lens in order to get: [2]

(i) an enlarged real image,

(ii) enlarged virtual image?

Answer

(i) In order to get an enlarged real image, the object should be placed between F₁ (or f) and 2F₁ (or 2f) distance i.e., 2F₁ > u > F₁.

(ii) In order to get an enlarged virtual image, the object should be placed between F₁ and optical centre i.e., u < F₁

Question 2(e)

A pond appears to be 2.7 m deep. If the refractive index of water is 4/3, find the actual depth of the pond. [2]

Answer

Given,

apparent depth = 2.7 m

Refractive index of the water = $\dfrac{4}{3}$

Refractive index of the liquid = $\dfrac{\text{Actual depth}}{\text{Apparent depth}}$

Substituting the values we get,

$\dfrac{4}{3} = \dfrac{\text{Actual depth}}{2.7} \\[0.5em] \Rightarrow \text{Actual depth} = \dfrac{4}{3} \times 2.7 = 3.6 \text{ m}$

Hence, actual depth = 3.6 m

Question 3(a)

The wave lengths for the light of red and blue colours are nearly 7.8 x 10^-7 m and 4.8 x 10^-7 m respectively. [2]

(i) Which colour has the greater speed in a vacuum?

(ii) Which colour has a greater speed in glass?

Answer

(i) The speed is same for both colours in vacuum because velocity of light of all colors in vacuum or air remains the same and it changes only when the medium changes.

(ii) The light of red colour has greater speed in glass as it has a larger wavelength.

Question 3(b)

Draw a graph between displacement from mean position and time for a body executing free vibration in a vacuum. [2]

Answer

Below is the graph between displacement from mean position and time for a body executing free vibration in a vacuum:

Question 3(c)

A sound wave travelling in water has wavelength 0.4 m. Is this wave audible in air? (The speed of sound in water = 1400 ms^-1) [2]

Answer

Given,

wavelength = 0.4 m

speed of sound in water = 1400 m s^-1

As we know,

frequency of wave = $\dfrac{\text{Speed}}{\text{Wavelength}}$

Substituting the values we get,

$\text{frequency of wave} = \dfrac{1400}{0.4} \\[0.5em] \text{frequency of wave} = 3500 \text{ Hz} = 3.5 \text{ kHz} \\[0.5em]$

Hence, we get the frequency of wave = 3500 Hz and this lies in the audible range of frequency (i.e., 20 Hz to 20,000 Hz), hence it is audible.

Question 3(d)

Why does stone lying in the sun get heated up much more than water lying for the same duration of time? [2]

Answer

The stone lying in the sun get heated up much more than water lying for the same duration of time because the specific heat capacity of water is much more than that of stone. With the same exposure to sun, stone acquires higher temperature due to it's low specific heat capacity.

Question 3(e)

Why is it not advisable to use a piece of copper wire as fuse wire in an electric circuit? [2]

Answer

It is not advisable to use a piece of copper wire as fuse wire in an electric circuit because due to it's high conductivity, low specific resistance and high melting point, copper does not melt when heated up and thus does not break the flow of current in the circuit. Thus, the purpose of fuse wire will not get fulfilled.

Question 4(a)

Calculate the total resistance across AB: [2]

Answer

This circuit consists of two parts. In the first part, the resistances 3 ohm and 6 ohm are connected in parallel. If R_p is the equivalent resistance then

$\dfrac{1}{R_p} = \dfrac{1}{3} + \dfrac{1}{6} \\[0.5em] \dfrac{1}{R_p} = \dfrac{2 + 1}{6} \\[0.5em] \dfrac{1}{R_p} = \dfrac{3}{6} \\[0.5em] \dfrac{1}{R_p} = \dfrac{1}{2} \\[0.5em] \Rightarrow R_p = 2 \space Ω$

Therefore, R_p = 2 Ω

In the second part, R_p (i.e., 2 ohm) and 5 ohm are in series. If the equivalent resistance = R_s the we get,

R_s = 2 + 5 = 7 Ω

Hence, equivalent resistance across A and B = 7 Ω

Question 4(b)

Two metallic blocks P and Q having masses in ratio 2 : 1 are supplied with the same amount of heat. If their temperatures rise by same degree, compare their specific heat capacities. [2]

Answer

Let mass of block P = m_p and mass of block Q = m_Q

Given,

$\dfrac{m_p}{m_Q}$ = $\dfrac{2}{1}$

Q = m x s x ∆t

Since, heat supplied (∆Q) and rise in temperature (∆t) is same for both block P and Q,

Therefore,

$m_p \times s_p \times ∆t = m_Q \times s_Q \times ∆t \\[0.5em] m_p \times s_p = m_Q \times s_Q \\[0.5em] \dfrac{s_p}{s_Q} = \dfrac{m_Q}{m_p} = \dfrac{1}{2}$

Therefore, s_P : s_Q = 1 : 2

Question 4(c)

When a current carrying conductor is placed in a magnetic field, it experiences a mechanical force. What should be the angle between the magnetic field and the length of the conductor so that the force experienced is: [2]

(i) Zero

(ii) Maximum?

Answer

(i) In order to experience zero force, the conductor should be parallel to the magnetic field i.e., the angle between the length of the conductor and the magnetic field should be zero.

(ii) In order to experience maximum force, the conductor should be kept perpendicular to the magnetic field i.e.,the angle between the length of the conductor and the magnetic field should be 90°.

Question 4(d)

A nucleus ₈₄X²⁰² of an element emits an alpha particle followed by a beta particle. The final nucleus is _aY^b. Find a and b. [2]

Answer

The emission of alpha and beta particle is represented below:

$_{84}^{202}\text{X} \longrightarrow \space _{82}^{198}\text{Z} + \space _{2}^{4}\text{He} \text{ (α particle emission)} \\[2em] _{82}^{198}\text{Z} \longrightarrow \space _{83}^{198}\text{Y} + \space _{-1}^{\space \space \space 0}e \text{ (β particle emission)}$

∴ a = 83 and b = 198

Question 4(e)

The diagram alongside shows a loop of wire carrying current I: [2]

(i) What is the magnetic polarity of the loop that faces us?

(ii) With respect to the diagram how can we increase the strength of the magnetic field produced by this loop?

Answer

(i) The magnetic polarity of the loop that faces us is south pole as the current is in clockwise direction.

(ii) We can increase the strength of the magnetic field produced by this loop by decreasing the value of variable resistance which in turn will increase the current I in the circuit.

Section II (40 Marks)

Question 5(a)

The figure alongside shows a simple pendulum of mass 200 g. It is displaced from the mean position A to the extreme position B. The potential energy at the position A is zero. At the position B the pendulum bob is raised by 5 m. [3]

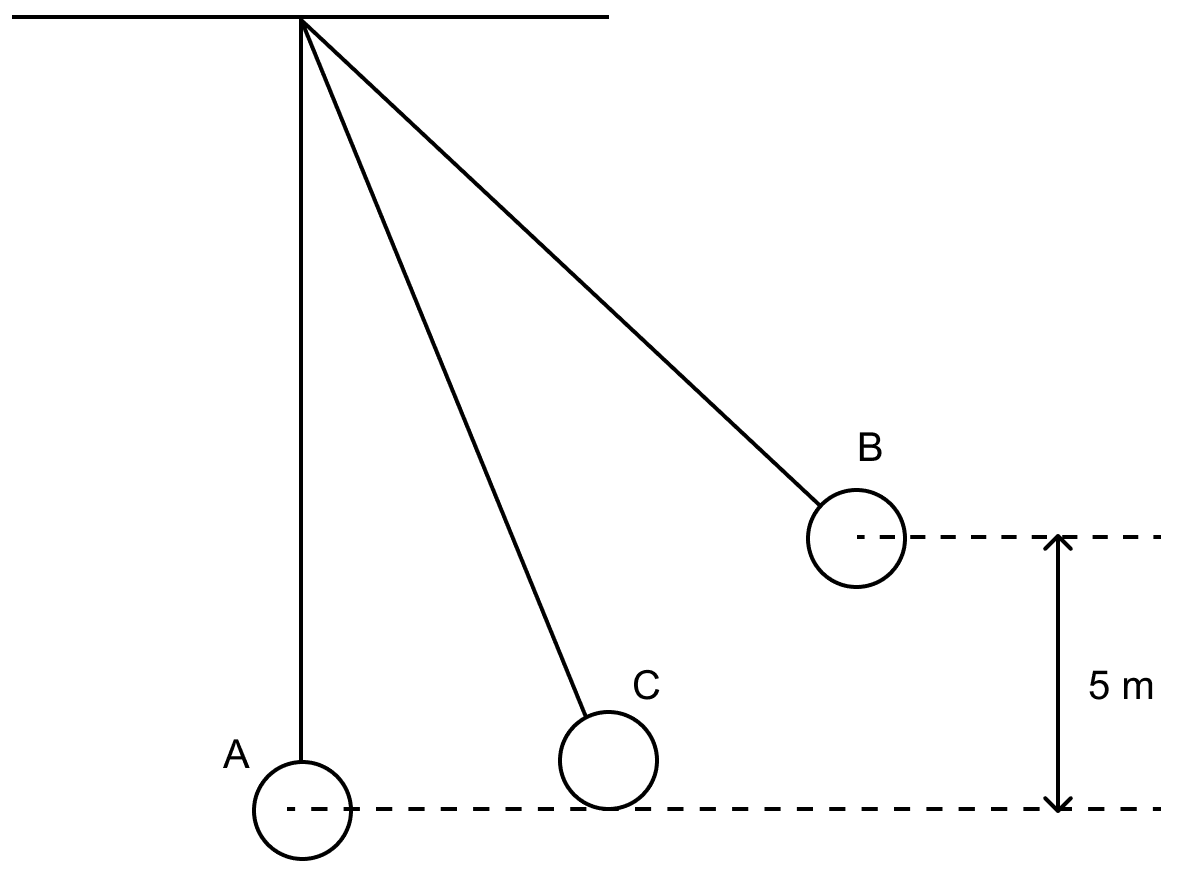
(i) What is the potential energy of the pendulum at the position B?

(ii) What is the total mechanical energy at point C?

(iii) What is the speed of the bob at the position A when released from B?

(Take g = 10 ms^-2 and there is no loss of energy.)

Answer

Given,

h = 5 m, m = 200 g = 0.2 kg, g = 10 ms^-2

(i) Potential energy U_B at B is given by

U_B = m x g x h

Substituting the values we get,

$U_B = 0.2 \times 10 \times 5 \\[0.5em] \Rightarrow U_B = 10 J$

Hence, the potential energy of the pendulum at the position B = 10 J

(ii) Total mechanical energy at point C = 10 J

The total mechanical energy is same at all points of the path due to conservation of mechanical energy.

(iii) At A, bob has only kinetic energy which is equal to potential energy at B,

Therefore,

$\dfrac{1}{2} \times m \times (v_A)^{2} = U_B \\[0.5em] 0.5 \times 0.2 \times (v_A)^{2} = 10 \\[0.5em] (v_A)^{2} = \dfrac{10}{0.1} \\[0.5em] \Rightarrow v_A = \sqrt{100} \\[0.5em] \Rightarrow v_A = 10 \text{ m s}^{-1}$

Question 5(b)

(i) With reference to the direction of action, how does a centripetal force differ from a centrifugal force during uniform circular motion? [3]

(ii) Is centrifugal force the force of reaction of centripetal force?

(iii) Compare the magnitudes of centripetal and centrifugal force.

Answer

(i) Centripetal force always acts towards the centre of circle along it's radius. It is this force which compels the body to move along the circular path. A centrifugal force appears to act away (outward) from the centre of circular path. Thus, the two forces act in opposite directions.

(ii) No, the centrifugal force is not the force of reaction of centripetal force.

(iii) Centripetal force and centrifugal force have equal magnitudes.

Question 5(c)

A block and tackle system of pulleys has velocity ratio 4. [4]

(i) Draw a neat, labelled diagram of the system indicating clearly the points of application and direction of load and effort.

(ii) What will be it's V.R. if the weight of the movable block is doubled?

Answer

(i) Labelled diagram of the system with direction and points of application of load and effort marked is shown below:

(ii) Increase in weight of movable block does not affect velocity ratio. Therefore, V.R. = 4.

Question 6(a)

A diver in water looks obliquely at an object AB in air. [3]

(i) Does the object appear taller, shorter or of the same size to the diver?

(ii) Show the path of two rays AC & AD starting from the tip of the object as it travels towards the diver in water and hence obtain the image of the object.

Answer

(i) The object appears taller to the diver.

(ii) Below diagram shows the path of two rays AC & AD:

Question 6(b)

Complete the path of the ray AB through the glass prism in PQR till it emerges out of the prism. Given the critical angle of the glass as 42°. [3]

Answer

The path of the ray AB through the glass prism in PQR till it emerges out of the prism is shown below:

Note that the total internal reflection takes place at C.

Question 6(c)

A lens of focal length 20 cm forms an inverted image at a distance 60 cm from the lens. [4]

(i) Identify the lens.

(ii) How far is the lens present in front of the object?

(iii) Calculate the magnification of the image.

Answer

(i) The lens used is convex lens.

(ii) Given, f = +20 cm, v = +60 cm, u = ?

From lens formula,

$\dfrac{1}{f}$ = $\dfrac{1}{v}$ - $\dfrac{1}{u}$

Substituting the values in the formula,

$\dfrac{1}{20} = \dfrac{1}{60} - \dfrac{1}{u} \\[0.5em] \Rightarrow \dfrac{1}{u} = \dfrac{1}{60} - \dfrac{1}{20} \\[0.5em] \Rightarrow \dfrac{1}{u} = \dfrac{1 - 3}{60} \\[0.5em] \Rightarrow \dfrac{1}{u} = \dfrac{- 2}{60} \\[0.5em] \Rightarrow u = - 30 cm \\[0.5em]$

Hence, the lens is 30 cm in front of the object

(iii) Magnification m = $\dfrac{v}{u}$

Substituting the values in the formula above we get,

$m = \dfrac{60}{- 30} = -2$

Thus, magnification = 2 times

Question 7(a)

Give reasons for the following: [3]

During the day:

(i) Clouds appear white.

(ii) Sky appears blue.

Answer

(i) Clouds are dust particles and water molecules suspended in the atmosphere near the earth of size bigger than the wavelength of visible light. Thus, they scatter all colours of incident white light from the sun to the same extent and hence when scattered light reaches our eyes, the clouds appear white.

(ii) The air molecules in the atmosphere scatter the blue end of spectrum having shorter wavelengths much more than colours on the red end. In the absence of direct light from sun, the light reaching our eyes is the scattered light which is rich in blue colour. Hence, light from all directions of sky being rich in blue colour makes the sky appear blue.

Question 7(b)

(i) Name the system which enables us to locate underwater objects by transmitting ultrasonic waves and detecting the reflecting impulse. [3]

(ii) What are acoustically measurable quantities related to pitch and loudness?

Answer

(i) The system which enables us to locate underwater objects by transmitting ultrasonic waves and detecting the reflecting impulse is called sound navigation and ranging or SONAR. Here, ultrasonic waves from a ship are transmitted in all directions. The reflected waves received in the receiver gives the distance and position of the object (e,g, submarine etc.) in water.

(ii) The acoustically measurable quantity related to pitch is frequency and to loudness is intensity of sound.

Question 7(c)

(i) When a tuning fork [vibrating] is held close to ear, one hears a faint hum. The same [vibrating tuning fork] is held such that it's stem is in contact with the table surface, then one hears a loud sound. Explain. [4]

(ii) A man standing in front of a vertical cliff fires a gun. He hears the echo after 3.5 seconds. On moving closer to the cliff by 84 m, he hears the echo after 3 seconds. Calculate the distance of the cliff from the initial position of the man.

Answer

(i) When the stem of the tuning fork is placed in contact with a table top, it sets the table surface in small vibrations but the large number of air molecules in contact with the table surface also start vibrating, thereby producing a loud sound.

(ii) Let the man be standing at distance d from the cliff and v be the speed of sound in air.

For first echo, t₁ = $\dfrac{2d}{v}$ = 3.5 s    [Eqn i ]

and for second echo, t₂ = $\dfrac{2(d - 84)}{v}$ = 3 s    [Eqn ii]

Dividing eqn (ii) by eqn (i)

$\dfrac{\dfrac{2(d - 84)}{v}}{\dfrac{2d}{v}} = \dfrac{3}{3.5} \\[0.5em] \Rightarrow \dfrac{d - 84}{d} = \dfrac{3}{3.5} \\[0.5em] \Rightarrow 3.5 (d - 84) = 3d \\[0.5em] \Rightarrow (3.5d) - (3.5 \times 84) = 3d \\[0.5em] \Rightarrow (3.5d) - 3d = 294 \\[0.5em] \Rightarrow 0.5 d = 294 \\[0.5em] \Rightarrow d = \dfrac{294}{0.5} \\[0.5em] \Rightarrow d = 588 m$

Hence, the distance of the cliff from the initial position of the man = 588 m

Question 8(a)

The diagram below shows the core of a transformer and it's input and output connections [3]

(i) State the material used for the core.

(ii) Copy and complete the diagram of the transformer by drawing input and output coils.

Answer

(i) The core is made up of soft iron.

(ii) The completed diagram of the transformer is shown below:

Question 8(b)

(i) What are superconductors? [3]

(ii) Calculate the current drawn by an appliance rated 110 W, 220 V when connected across 220 V supply.

(iii) Name a substance whose resistance decreases with the increase in temperature.

Answer

(i) A superconductor is a substance of zero resistance (or infinite conductance) at a very low temperature.

(ii) For the given appliance, W = 110 W, V = 220 V

$\therefore \text{Current I} = \dfrac{W}{V} = \dfrac{110}{220} = 0.5 \text{ A}$

Hence, current drawn by the appliance = 0.5 A

(iii) The resistance of semi conductors such as carbon, silicon, etc., decreases with increase in temperature.

Question 8(c)

The diagram alongside shows three resistors connected across a cell of e.m.f. 1.8 V and internal resistance r. Calculate: [4]

(i) Current through 3 Ω resistor.

(ii) The internal resistance r.

Answer

(i) The equivalent resistance R_p of resistances 3 Ω and 1.5 Ω joined in parallel is given by

$\dfrac{1}{R_p} = \dfrac{1}{3} + \dfrac{2}{3} \space \space \big[\because 1.5 Ω = \dfrac{3}{2} Ω\big] \\[0.5em] \Rightarrow \dfrac{1}{R_p} = \dfrac{3}{3} \\[0.5em] \Rightarrow R_p = 1 Ω$

From, V = IR

the potential drop across this combination = 0.3 x 1 = 0.3 V

$\therefore \text{Current through 3 Ω resistance} = \dfrac{\text{Voltage}}{\text{Resistance}} \\[0.5em] = \dfrac{0.3}{3} = 0.1 \text{ A}$

(ii) Total resistance of the circuit = R_p + 4 + r = (5 + r) Ω

Current in the circuit,

$0.3 = \dfrac{1.8}{5 + r} \\[0.5em] 0.3 \times (5 + r) = 1.8 \\[0.5em] (0.3 \times 5) + (0.3 \times r) = 1.8 \\[0.5em] 1.5 + (0.3 \times r) = 1.8 \\[0.5em] 0.3 \times r = 1.8 - 1.5 \\[0.5em] r = \dfrac{0.3}{0.3} = 1 Ω$

∴ Internal resistance r = 1 Ω

Question 9(a)

(i) Define heat capacity of a substance. [3]

(ii) Write the SI unit of heat capacity.

(iii) What is the relationship between heat capacity and specific heat capacity of a substance?

Answer

(i) The heat required to raise the temperature of a substance or body through 1 °C (or 1 K) is called it's heat capacity.

(ii) S.I. unit of heat capacity is J °C^-1 or J K^-1

(iii) Specific heat capacity = $\dfrac{\text{Heat capacity}}{\text{Mass of body or substance}}$

Question 9(b)

The diagram below shows the change of phases of a substance on a temperature vs time graph on heating the substance at a constant rate.[3]

(i) Why is the slope of CD less than slope of AB?

(ii) What is the boiling and melting point of the substance?

Answer

(i) In part CD, the rate of rise in temperature is slow as the substance in this phase has high specific heat capacity while temperature rises rapidly in part AB (so higher slope) as the substance has lower specific heat capacity in this phase. The different specific heat capacities are attributed to different phases of state (i.e. solid and liquid phase).

(ii) Boiling point of substance is t₂ and melting point of substance is t₁

Question 9(c)

A piece of ice of mass 60 g is dropped into 140 g of water at 50 °C. [4]
Calculate the final temperature of water when all the ice has melted. (Assume no heat is lost to the surrounding).
Specific heat capacity of water (c) = 4.2 Jg^-1k^-1,
Specific latent heat of fusion of ice (L) = 336 Jg^-1

Answer

Let final temperature of water be T °C.

Heat energy taken by the ice to melt at 0 °C

Q₁ = mass of ice x specific latent heat of fusion of ice
= 60 x 336 = 20,160 J

Heat energy taken by the melted ice to raise it's temperature from 0 °C to T °C.

Q₂ = mass of ice x specific heat capacity of water x rise in temperature
= 60 x 4.2 x (T - 0) = 252T J

Total heat energy taken by ice = Q₁ + Q₂
= (20,160 + 252 T) J

Heat energy given by water in fall of it's temperature from 50 °C to T °C
= mass of water x specific heat capacity of water x fall in temperature
= 140 x 4.2 x (50 - T)
= 588 (50 - T) J

If there is no heat loss,

heat energy given by water = total heat energy taken by ice

Substituting the values we get,

$588 (50 - T) = 20,160 + 252 T \\[0.5em] (588 \times 50) - 588 T = 20,160 + 252 T \\[0.5em] 29,400 - 588 T = 20,160 + 252 T \\[0.5em] 29,400 - 20,160 = 588 T + 252 T \\[0.5em] 9240 = 840 T \\[0.5em] \Rightarrow T = \dfrac{9240}{840} \\[0.5em] \Rightarrow T = 11 °C$

Hence, T = 11 °C

Question 10(a)

(i) Draw a neat labeled diagram of a d.c. motor. [3]

(ii) Write any one use of a d.c. motor.

Answer

(i) Below is the labeled diagram of a d.c. motor:

(ii) It is used to produce rotational motion in appliances like fan, mixer, grinder, washing machine etc.

Question 10(b)

(i) Differentiate between nuclear fusion and nuclear fission. [3]

(ii) State one safety precaution in the disposal of nuclear waste.

Answer

(i) The difference between nuclear fusion and nuclear fission is as follows :

(ii) The nuclear waste should be enclosed in thick casks and buried in deep underground places far from populated areas as they can be harmful.

Question 10(c)

An atomic nucleus A is composed of 84 protons and 128 neutrons. The nucleus A emits an alpha particle and is transformed into a nucleus B. [4]

(i) What is the composition of B?

(ii) The nucleus B emits a beta particle and is transformed into a nucleus C. What is the composition of C?

(iii) What is mass number of the nucleus A?

(iv) Does the composition of C change if it emits gamma radiations?

Answer

(i) After the emission of an alpha particle from A, the resulting nucleus B has 2 protons and 2 neutrons less than the part nucleus (i.e., A), therefore, the nucleus B has :
No. of proton = 82
No of neutron = 126

(ii) After the emission of a beta particle from B, the resulting nucleus C 1 proton more and 1 neutron less than the part nucleus (i.e., B) therefore, the nucleus C has :
No. of proton = 83
No. of neutron = 125

(iii) Mass number of the nucleus A = (84 + 128 ) = 212.

(iv) No, the composition of a nucleus does not change if it emits gamma radiation.