Force

Exercise 1(A)

Question 1

State the condition when on applying a force, a body has:

(a) translational motion

(b) rotational motion.

Answer

(a) Translation motion is produced when a body is free to move.

(b) Rotational motion is produced when the body is fixed at a point.

Question 2

Define moment of force and state its S.I. unit.

Answer

The moment of force is equal to the product of the magnitude of the force applied and the perpendicular distance of the line of action of the force from the axis of rotation(or pivoted point).

The S.I unit of moment of force is Newton × meter = Newton meter (Nm)

Question 3

State whether the moment of force is a scalar or vector quantity?

Answer

The moment of force is a vector quantity.

Question 4

State two factors affecting the turning effect of a force.

Answer

The following are the two factors on which moment of force about a point depends

(a) The magnitude of the force applied and,

(b) The distance of the line of action of the force from the axis of rotation(or the pivoted point).

Question 5

When does a body rotate? State one way to change the direction of rotation of a body. Give a suitable example to explain your answer.

Answer

If a body is pivoted at a point and the force is applied on the body at a suitable point, it rotates the body about the axis passing through the pivoted point.

The direction of rotation can be changed by changing the direction of force.

Figures given below shows the clockwise and anticlockwise movement in a circle pivoted at the centre by changing the point of application of force F from A to point B

Question 6

Write the expression for the moment of force about a given axis.

Answer

The expression for the moment of force is given by

Moment of force about a given axis = Force × perpendicular distance of force from the axis of rotation.

Question 7

What do you understand by the clockwise and anticlockwise moment of force? When is it taken positive?

Answer

If the effect on the body is to turn it clockwise, moment of force is called the clockwise moment and it is taken as negative, while if the effect on the body is to turn it anticlockwise, moment of force is called the anticlockwise moment and it is taken as positive.

Question 8

State one way to reduce the moment of a given force about a given axis of rotation.

Answer

The moment of force can be reduced by decreasing the perpendicular distance of force from the axis of rotation.

Question 9

State one way to obtain a greater moment of a force about a given axis of rotation.

Answer

We can obtain a greater moment of force by increasing the perpendicular distance of force from the axis of rotation.

Question 10

Why is it easier to open a door by applying the force at the free end of it?

Answer

It is easier to open the door by applying the force at the free end because when the perpendicular distance is large less force is required to turn the body.

Question 11

The stone of hand flour grinder is provided with a handle near its rim. Give a reason.

Answer

The stone of hand flour grinder is provided with a handle near its rim so that by applying small force at the handle it can be rotated easily about the fixed point at its centre.

Question 12

It is easier to turn the steering wheel of a large diameter than that of a small diameter. Give reason.

Answer

It is easier to turn the steering wheel of a large diameter in comparison to the wheel of a smaller diameter as less force is required in the first case due to the larger distance from the centre of the rim.

Question 13

A spanner (or wrench) has a long handle. Why?

Answer

A spanner is provided with a long handle so as to create a larger turning moment with less force.

Question 14

A jack screw is provided with a long arm. Explain why?

Answer

A jack screw which is used to lift a heavy vehicle has a long arm so that less force is needed to rotate it to raise or lower the vehicle.

Question 15

A, B and C are the three forces each of magnitude 4N acting in the plane of paper as shown in figure. The point O lies in the same plane.

(i) Which force has the least moment about O? Give reason.

(ii) Which force has the greatest moment about O? Give reason.

(iii) Name the forces producing (a) clockwise, (b) anticlockwise moments.

(iv) What is the resultant torque about the point O?

Answer

(i)
We know that,

Moment of force = Force × Perpendicular distance

We can see from the given figure that vector C has least perpendicular distance from point O.

Hence, vector C will have least moment about O.

(ii)
We know that,

Moment of force = Force × Perpendicular distance

We can see from the given figure that vector A has greatest perpendicular distance from point O

Hence, vector A will have greatest moment about O.

(iii)
(a) Clockwise moments are produced by vectors A and B.

Reason : If turning effect on the body is clockwise then moment of force is called clockwise moment and it is taken as a negative value.

(b) Anticlockwise moment is produced by vector C.

Reason : If turning effect on the body is anticlockwise then moment of force is called anticlockwise moment and it is taken as a positive value.

(iv)
Sum of torques due to vectors A, B and C = Resultant torque about point O

$-(4 \times 0.9) - (4 \times 0.8) + (4 \times 0.6)Nm \\[0.5em] = -3.6 - 3.2 + 2.4 Nm \\[0.5em] = -4.4 Nm$

So, the resultant torque is 4.4Nm (clockwise direction).

Question 16

The adjacent diagram shows a heavy roller, with its axle at O, which is to be raised on a pavement XY. If there is friction between the roller and pavement, show by an arrow on the diagram the point of application and the direction of force to be applied. If pivoted at 0, now will it go up?

Answer

Application of Force has to be done as shown in the diagram.

No, if pivoted at O it will not go up.

Question 17

A body is acted upon by two forces each of magnitude F, but in opposite directions. State the effect of the forces if

(a) both forces act at the same point of the body.

(b) the two forces act at two different points of the body at a separation r.

Answer

(a) As two forces of same magnitude are acting on a body at the same point and they are in opposite direction so the resultant force will be zero.

F – F = 0

(b) When two forces of same magnitude act on a body at two different points at a separation r and in opposite direction then the moment of force will be Fr

Moment of forces = F × r

Question 18

Draw a neat labelled diagram to show the direction of two forces acting on a body to produce rotation in it. Also mark the point O about which the rotation takes place.

Answer

Two forces of magnitude F act at point A and point B. The body rotates in anticlockwise direction.

Question 19

What do you understand by the term couple? State its effect on a body. Give two examples in our daily life where couple is applied to turn a body.

Answer

Two equal and opposite parallel forces, not acting along the same line form a couple.

A couple is always needed to produced a rotation.

Two examples in our daily life where we use couple are:

1. Turning a water tap.
2. Tightening the cap of a bottle.

Question 20

Define the moment of a couple. Write its S.I unit.

Answer

Moment of couple is product of either force and the perpendicular distance between the two forces.

The S.I unit of moment of couple is Nm

Question 21

Prove that

Moment of couple = Force x Couple arm.

Answer

At point A and point B two forces act which rotate the bar in anticlockwise direction.

The perpendicular distance between the two forces called AB is the couple arm.

Moment of force F at A = F x OA (anticlockwise)

Moment of force F at B = F x OB (anticlockwise)

Total moment of couple = F x OA + F x OB

F x (OA + OB) = F x AB

= F x d

Hence proved : Moment of force = Force x Couple arm

Question 22

What do you mean by equilibrium of a body?

Answer

When a number of forces acting on a body produce no change in its state of rest or of linear or rotational motion, the body is said to be in equilibrium.

Question 23

State the condition when a body is in

(i) static equilibrium.

(ii) dynamic equilibrium.

Give one example each of static and dynamic equilibrium.

Answer

(i) When a body remains in the state of rest under the influence of several forces, the body is said to be in static equilibrium.

Example — A toy lying on a floor is in static equilibrium.

(ii) When a body remains in the same state of motion (translation or rotational), under the influence of several forces, the body is said to be in dynamic equilibrium.

Example — An apple falling from a tree with a constant velocity.

Question 24

State two conditions for a body, acted upon by several forces to be in equilibrium.

Answer

The two conditions for a body to be in equilibrium are

1. The resultant of all the forces acting on a body should be zero.

2. The algebraic sum of moments of all the forces acting on the body about the point of rotation should be zero.

Question 25

State the principle of moments. Name one device based on it.

Answer

According to the principle of moments, if the algebraic sum of moments of all the forces, acting on the body, about the axis of rotation is zero, the body is in equilibrium. Therefore, as per the principle of moments,

sum of anticlockwise moments = sum of clockwise moments

For example, a physical balance works on the principle of moments.

Question 26

Describe a simple experiment to verify the principle of moments, if you are supplied with a metre rule, a fulcrum and two springs with slotted weights.

Answer

When we hang a metre rule horizontally from a fixed support with the help of a strong thread at point O as shown.

We use two slotted weights W₁ and W₂

We hang two spring balances on either side of the thread. The metre rule may tilt to one side.

We adjust the two spring balance distances from the support by keeping one at A and the other at B so that the scale again becomes horizontal.

Let W₁ at a distance OA = l₁ be the weight suspended on the right side of thread from the spring balance at A, while W₂ at a distance OB = l₂ be the weight suspended on the left side of thread from the spring balance at B.

The weight W₁ tends to turn the scale clockwise and the weight W₂ tends to turn the scale anticlockwise.

Clockwise moment = W₁ × l₁

Anticlockwise moment = W₂ × l₂

In equilibrium, when the scale is horizontal, it is found that

Clockwise moment = Anticlockwise moment

So, W₁l₁ = W₂l₂

Hence, the principle of moments is proved.

Question 27

Complete the following sentences:

(i) The S.I. unit of moment of force is Newton metre (Nm)

(ii) In equilibrium algebraic sum of moments of all forces about the point of rotation is zero.

(iii) In beam balance when the beam is balanced in a horizontal position, it is in static equilibrium.

(iv) The moon revolving around the earth is in dynamic equilibrium.

Multiple Choice Type

Question 1

The moment of a force about a given axis depends:

1. only on the magnitude of force
2. only on the perpendicular distance of force from the axis
3. neither on the force nor on the perpendicular distance of force from the axis
4. both, on the force and its perpendicular distance from the axis. ✓

Question 2

A body is acted upon by two unequal forces in opposite directions, but not in the same line. The effect is that:

1. the body will have only the rotational motion
2. the body will have only the translational motion
3. the body will have neither the rotational motion nor the translational motion
4. the body will have rotational as well as translational motion. ✓

Numericals

Question 1

The moment of a force of 10N about a fixed point O is 5Nm. Calculate the distance of the point O from the line of action of the force.

Answer

As we know,

Moment of Force = Force × Perpendicular distance from the point O

Moment of force = F × r

So, putting the values from the question we get

$5Nm = 10r \\[0.5em] r = \dfrac{5}{10} \\[0.5em] \therefore r = 0.5m$

Question 2

A nut is opened by a wrench of length 10cm. If the least force required is 5.0N, find the moment of force needed to turn the nut.

Answer

It is given that,

Required least force = 5N

r = 10cm = 0.1m

We know, Moment of force = F x r

Substituting the values of F and r

$5 \times 0.1 = 0.5Nm$

Therefore, moment of force = 0.5 Nm

Question 3

A wheel of diameter 2m is shown in figure with axle at O. A force F = 2N is applied at B in the direction shown in figure.

Calculate the moment of force about

(i) the centre O, and

(ii) the point A.

Answer

We know from the question,

F = 2 N
Diameter = 2m
So, Radius or OB = 1m

(i) Moment of force at O = F x r

Substituting the values of F and r we get,

$2 \times 1 = 2Nm$

(ii) Moment of force at A = F x r

Substituting the values of F and r we get,

$2 \times 2 = 4Nm$

Question 4

The diagram shows two forces F1 = 5N and F2 = 3N acting at points A and B of a rod pivoted at a point O, such that OA = 2m and OB = 4m

Calculate:

(i) the moment of force F1 about O.

(ii) the moment of force F2 about O.

(iii) total moment of the two forces about O.

Answer

Given,

OA = 2m
OB = 4m
F1 = 5N
F2 = 3N

As we know,

Moment of force = F x r

Substituting the values of F and r

(i) Moment of force F1 about O

$5 \times 2 = 10Nm$

Therefore, moment of force F1 about O is 10Nm (anticlockwise)

(ii) Moment of force F2 about O

$3 \times 4 = 12Nm$

Therefore, moment of force F2 about O is 12Nm (clockwise)

(iii) Total moment of two forces about midpoint is

$12 - 10 = 2Nm$

Therefore, total moment of two forces about O is 2Nm (clockwise)

Question 5

Two forces each of magnitude 10N act vertically upwards and downwards respectively at the two ends A and B of a uniform rod of length 4m which is pivoted at its mid-point O as shown. Determine the magnitude of resultant moment of forces about the pivot O.

Answer

Given,
Ab = 4m
OA = 2m
OB = 2m
Force at A = 10N
Force at B = 10N

As we know ,

Moment of force = F x r

Substituting the values of F and r

Moment of force about o at point A

$10 \times 2 = 20Nm \text{ clockwise}$

Moment of force about o at point B

$10 \times 2 = 20Nm \text{ clockwise}$

Total moment of forces about the centre O

$20 + 20 = 40Nm \\[0.5em]$

Total moment of force about the pivot O is 40 Nm (clockwise)

Question 6

Figure shows two forces each of magnitude 10N acting at the points A and B at a separation of 50 cm, in opposite directions. Calculate the resultant moment of the two forces about the point (i) A, (ii) B and (iii) O, situated exactly at the middle of the two forces.

Answer

Given,
Force at A = 10N
Force at B = 10N
Distance between A and B = 50cm = 0.5m

(i) Resultant moment of two forces at point A is

$10 \times 0.5 = 5Nm \text{ clockwise} \\[0.5em]$

Therefore, resultant moment of two forces at point A is 5 Nm (clockwise)

(ii) Resultant moment of two forces at point B is

$10 \times 0.5 = 5Nm \text{ clockwise} \\[0.5em]$

Therefore, resultant moment of two forces at point B is 5 Nm (clockwise)

(iii) Perpendicular distance of point O from either of the forces F = 10N is 0.25 m

Moment of force F at point A about O

$10 \times 0.25 =2.5Nm \text{ clockwise} \\[0.5em]$

Moment of force F at point B about O

$10 \times 0.25 =2.5Nm \text{ clockwise} \\[0.5em]$

Resultant moment of two forces about o is

$2.5 + 2.5 = 5Nm \text{ clockwise} \\[0.5em]$

Therefore, Resultant moment of two forces about o is 5Nm (clockwise)

Question 7

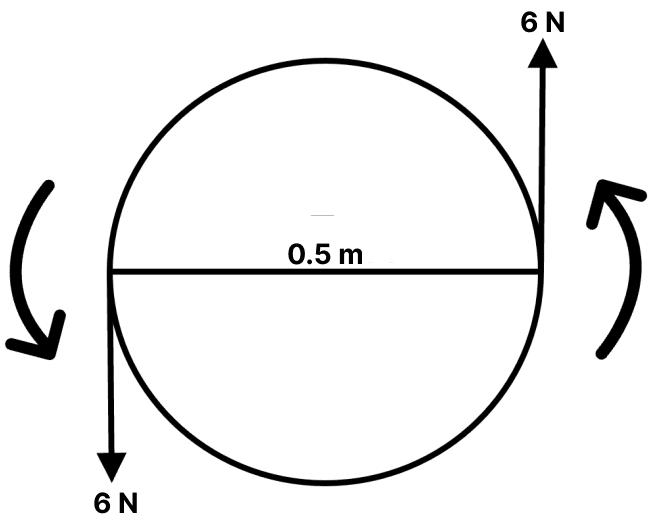
A steering wheel of diameter 0.5m is rotated anti-clockwise by applying two forces each of magnitude 5N. Draw a diagram to show the application of forces and calculate the moment of forces applied.

Answer

Moment of couple = either force × couple arm

$5 \times 0.5 =2.5Nm \\[0.5em]$

Question 8

A uniform metre rule is pivoted at its mid-point. A weight of 50 gf is suspended at one end of it. Where should a weight of 100gf be suspended to keep the rule horizontal?

Answer

Let us assume that a 50 gf weight produces an anticlockwise moment about the middle point ( 50 cm ).

Now, if a weight of 100 gf produces a clockwise moment about the middle point and d cm be the distance from the middle.

As we know, the principle of moments states that

Anticlockwise moment = Clockwise moment.

$50 gf \times 50cm = 100gf \times d cm \\[0.5em] \Rightarrow d = \dfrac{50\times50}{100}\\[0.5em] \Rightarrow d = 25 cm$

Therefore, a weight of 100gf will be suspended at a distance of 25cm to keep the ruler balanced.

Question 9

A uniform metre rule balances horizontally on a knife edge placed at the 58 cm mark when a weight of 20gf is suspended from one end. (i) Draw a diagram of the arrangement. (ii) What is the weight of the rule?

Answer

(i) Diagram of the arrangement is shown below:

(ii) As we know, the principle of moments states that

Anticlockwise moment = Clockwise moment.

$W \times (58-50) = 20gf \times (100-58) \\[0.5em] \Rightarrow W = \dfrac{20\times42}{8} \\[0.5em] \Rightarrow W = 105 gf$

Question 10

The diagram shows a uniform bar supported at the middle point O. A weight of 40 gf is placed at a distance 40cm to the left of the point O. How can you balance the bar with a weight of 80 gf?

Answer

From the given figure we can see that,

Anticlockwise moment = 40 gf × 40 cm
Clockwise moment = 80 gf × d cm

As we know, the principle of moments states that

Anticlockwise moment = Clockwise moment.

$40gf \times 40cm = 80gf \times d \\[0.5em] \Rightarrow d = \dfrac{40 \times 40}{80}\\[0.5em] \Rightarrow d = 20 cm \\[0.5em]$

Therefore the bar will be in balanced position if weight of 80gf is placed at a point of 20cm to the right of O.

Question 11

Figure shows a uniform metre rule placed on a fulcrum at its mid-point O and having a weight 40gf at the 10 cm mark and a weight of 20 gf at the 90 cm mark.

(i) Is the metre rule in equilibrium? If not, how will the rule turn?

(ii) How can the rule be brought in equilibrium by using an additional weight of 40gf?

Answer

(i) We know that when anticlockwise moment is equal to clockwise moment then the rule will be in equilibrium.

Let us check,

(a) Anticlockwise moment = Fr

$40gf \times (50-10)cm = 40 \times 40 \\[0.5em] = 1600 gfcm$

Clockwise moment = Fr

$20gf \times (90-50)cm = 20 \times 40 \\[0.5em] = 800gfcm$

So, the meter rule will not be in equilibrium. It will turn in anticlockwise direction.

(ii) To balance the rule in equilibrium 40gf should be kept on right side.

Let distance from middle = d cm

So clockwise moment becomes

$800 gf cm + (40gf \times d cm)$

As we know, the principle of moments states that

Anticlockwise moment = Clockwise moment

$1600gfcm = 800gfcm + 40gf \times d cm$

Therefore,

$d = \dfrac{800}{40} = 20cm$

So, the additional weight should be placed at 70cm mark to bring the rule in equilibrium.

Question 12

When a boy weighing 20 kgf sits at one end of a 4m long see-saw, it gets depressed at its end. How can it be brought to the horizontal position by a man weighing 40 kgf.

Answer

As we know, the principle of moments states that

Anticlockwise moment = Clockwise moment

$20 Kgf \times 2m = 40 Kgf \times d \\[0.5em] \Rightarrow d = \dfrac{20 \times 2}{40} \\[0.5em] \Rightarrow d = 1m$

So it is proved that horizontal position can be achieved if a person sits at a distance of 1m from the centre on the side opposite to the boy.

Question 13

A physical balance has its arms of length 60 cm and 40 cm. What weight kept on a pan of longer arm will balance an object of weight 100 gf kept on other pan?

Answer

As we know, the principle of moments states that

Anticlockwise moment = Clockwise moment

$100gf \times 40cm = W \times 60cm$

Weight on the longer pan

$W = \dfrac{(100 \times 40) }{60} \\[0.5em] W = 66.67gf$

So, a weight of 66.67gf kept on the pan of longer arm will balance the object of weight 100 gf kept on the other pan.

Question 14

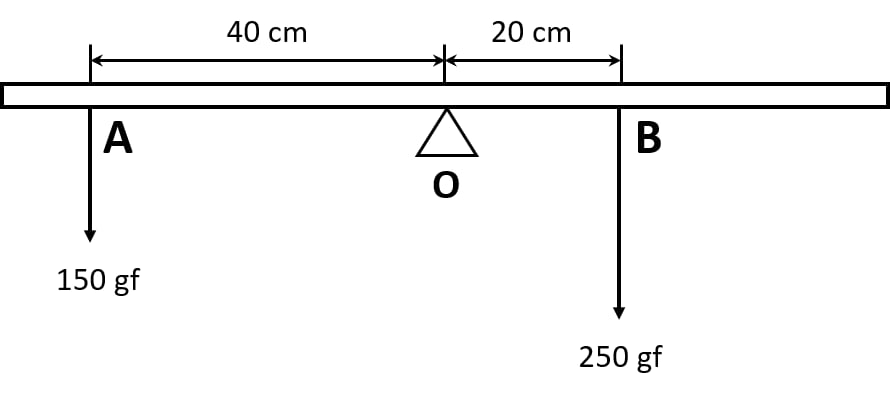
The diagram shows a uniform meter rule weighing 100 gf, pivoted at its centre O. Two weights 150gf and 250gf hang from the point A and B respectively of the metre rule such that OA = 40 cm and OB = 20 cm.

Calculate:

(i) the total anticlockwise moment about O,

(ii) the total clockwise moment about O,

(iii) the difference of anticlockwise and clockwise moment, and

(iv) the distance from O where a 100gf weight should be placed to balance the metre rule.

Answer

(i) The total anticlockwise moment about the centre o

$= 150gf \times 40cm \\ = 6000gf cm$

The total clockwise moment about the centre o

$= 250gf \times 20cm \\[0.5em] = 5000gf cm \\[0.5em]$

(iii) The difference of anticlockwise and clockwise moment

$= 6000 - 5000 \\[0.5em] = 1000gf cm \\[0.5em]$

(iv) As we know, the principle of moments states that

Anticlockwise moment = Clockwise moment

$150gf \times 40cm = 250gf \times 20cm + 100gf \times d \\[0.5em] 6000gf = 5000gf +100gf \times d \\[0.5em] d = \dfrac {1000}{100} \\[0.5em] d = 10cm$

So d = 10 cm on the right side of o

Question 15

A uniform metre rule of weight 10 gf is pivoted at its 0 mark.

(i) What moment of force depresses the rule?

(ii) How can it be made horizontal by applying a least force?

Answer

(i) Moment of force = Fr

Substituting the values of F and r we get,

$10gf \times 50cm = 500gfcm$

In order to make the rule horizontal by applying least force distance has to be max as moment of force will remain same.

So,

$F = \dfrac{500}{100} = 5gf$

Therefore, a force of 5 gf upwards at 100 cm can balance the rule.

Question 16

A uniform half metre rule can be balanced at the 29.0 cm mark when a mass 20g is hung from its one end.

(a) Draw a diagram of the arrangement.

(b) Find the mass of the half metre rule.

(c) In which direction would the balancing point shift if 20g mass is shifted inside from its one end?

Answer
(a) Diagram of the arrangement is shown below:

(b) Suppose, if the mass of the meter rule be M.

Given, uniform meter rule, so weight (Mg) will act at 25 cm.

Mg produces anticlockwise moment about point o.

Now, in order to balance the 20g weight is tied at 50cm point and it acts in the clockwise direction.

As we know, the principle of moments states that

Anticlockwise moment = Clockwise moment

$Mg(29 - 25) = 0.02 g (50-29) \\[0.5em] M = \dfrac{21\times 0.02}{4} \\[0.5em] = 0.105 kg \\[0.5em] = 105g$

The weight of half the meter rule is 105 g.

(c) The balancing point will shift towards the 25 cm mark.

Question 17

A uniform metre rule of mass 100 g is balanced on a fulcrum at mark 40 cm by suspending an unknown mass m at the mark 20 cm.

(i) Find the value of m.

(ii) To which side the rule will tilt if the mass m is moved to the mark 10 cm?

(iii) What is the resultant moment now?

(iv) How can it be balanced by another mass 50 g?

Answer

(i) As we know, the principle of moments states that

Anticlockwise moment = Clockwise moment

$100g \times (50-40)cm = m \times (40-20)cm \\[0.5em] \Rightarrow 100 \times 10 = m \times 20 \\[0.5em] \Rightarrow m = 50g \\[0.5em]$

(ii) When the mass m is shifted to mark 10cm , it results in rule being shifted on the side of mass m in anticlockwise direction.

(iii) Anticlockwise moment is produced when a mass of m grams is moved towards the mark of 10cm.

$100gf \times (50-40)cm = 1000gfcm$

Therefore, the resultant moment will be

$1500gfcm - 1000 gfcm = 500gfcm (anticlockwise)$

(iv) As we know, the principle of moments states that

Anticlockwise moment = Clockwise moment

So,

$100gf \times (50-40)cm + 50gf \times d = 50gf \times (40-10)cm \\[0.5em] \Rightarrow 1000gfcm + 50gf \times d = 1500gfcm \\[0.5em] \Rightarrow 50gfd = 500gfcm \\[0.5em] \Rightarrow d = 10 cm$

Hence, we can balance 50gm at 50cm

Question 18

In figure below, a uniform bar of length l m is supported at its ends and loaded by a weight W kgf at its middle. In equilibrium, find the reactions R1 and R2 at the ends.

Answer

As we know, the principle of moments states that

Anticlockwise moment = Clockwise moment

R₁ + R₂ = W

Given, the system is in equilibrium so

$R_{1}\times\dfrac{l}{2} = R_{2}\times\dfrac{l}{2}$

Since, R₁ = R₂ and 2R₁ = W

Therefore, R₁ = W/2 = R₂

Exercise 1(B)

Question 1

Define the term 'centre of gravity of a body'.

Answer

The centre of gravity of of a body is defined as the point about which the algebraic sum of moments of weights of particles constituting the body is zero and the entire weight of the body is to act at this point.

Question 2

Can the centre of gravity of a body be situated outside its material of the body? Give an example.

Answer

Yes, the centre of gravity can be outside the material of the body.

In the case of a uniform ring the centre of gravity is in the centre of the ring and that point is outside the material of the ring.

Question 3

State a factor on which the position of centre of gravity of a body depend? Explain your answer with an example.

Answer

The position of the centre of gravity of any body will depend on the type of shape it has i.e. (on the distribution of mass on the body) in it. It changes if the shape of the body is deformed.

For example, the centre of gravity of a wire is a its mid point. However, if the wire is turned in a way that it makes a circle then its centre of gravity will be at the centre of the circle.

Question 4

What is the position of centre of gravity of a:

(a) rectangular lamina
(b) cylinder?

Answer

Centre of gravity for the following figures are as follows :

(a) Rectangular lamina — at the point of intersection of the diagonals.

(b) Cylinder — at the mid point of the axis of cylinder.

Question 5

At which point is the centre of gravity situated in :

(a) A triangular lamina and

(b) A circular lamina?

Answer

The centre of gravity for the following figures are as follows :

(a) A triangular lamina — at the point of intersection of the medians.

(b) A circular lamina — at the centre of the circular lamina.

Question 6

Where is the centre of gravity of a uniform ring situated?

Answer

The centre of gravity of a uniform ring is situated at the centre of the ring.

Question 7

A square card board is suspended by passing a pin through a narrow hole at its one corner. Draw a diagram to show its rest position. In the diagram mark the point of suspension by the letter S and centre of gravity by the letter G.

Answer

The diagram is shown below:

Question 8

Explain how you will determine experimentally the position of centre of gravity for a triangular lamina (or a triangular piece of card board).

Answer

To determine centre of gravity for a triangular lamina, make three fine holes a, b, c near its edges. After that, suspend it from hole a along with a plumb line. Ensure that the lamina is freely suspended. When it comes to rest, draw straight line ad along the plumb line. Repeat the experiment by suspending the lamina through hole 'b' and then through hole 'c'. This gives us two straight lines, be and cf respectively. The three lines ad, be and cf intersect each other at a common point G. This common point G is the position of the centre of gravity of triangular lamina.

Question 9

State whether the following statements are true or false.

(i) 'The position of centre of gravity of a body remains unchanged even when the body is deformed'.
False

(ii) 'The centre of gravity of a freely suspended body always lies vertically below the point of suspension'.
True

Question 10

A uniform flat circular rim is balanced on a sharp vertical nail by supporting it at a point A, as shown in figure. Mark the position of centre of gravity of the rim in the diagram by the letter G.

Answer
The position of centre of gravity of the rim is marked by the letter G in the below diagram:

Question 11

Figure shows three pieces of card board of uniform thickness cut into three different shapes. On each diagram draw two lines to indicate the position of centre of gravity G.

Answer

The position of centre of gravity G for the three pieces of card board are marked in the below diagrams:

Multiple Choice Type

Question 1

The centre of gravity of a uniform ball is

1. At its geometrical centre ✓
2. at its bottom
3. at its topmost point
4. at any point on its surface

Question 2

The centre of gravity of a hollow cone of height h is at distance x from its vertex where the value of x is:

1. h/3
2. h/4
3. 2h/3 ✓
4. 3h/4

Exercise 1(C)

Question 1

Explain the meaning of uniform circular motion. Why is such motion said to be accelerated?

Answer

When a body moves with a constant speed in a circular path, its motion is said to be in uniform circular motion.

Uniform circular motion is said to be accelerated as the velocity changes with continuous change in direction of motion.

Question 2

Draw a neat labelled diagram for a particle moving in a circular path with a constant speed. In your diagram show the direction of velocity at any instant.

Answer

The below diagram shows a particle moving in a circular path with a constant speed and its direction of velocity:

Question 3

Is it possible to have an accelerated motion with a constant speed? Name such type of motion.

Answer

Yes, an accelerated motion with constant speed is possible. Uniform circular motion is such type of motion.

Question 4

Give one example of motion in which speed remains uniform, but the velocity changes.

Answer

Motion of artificial satellite is one of the cases where speed is same however velocity changes.

Question 5

A uniform circular motion is an accelerated motion. Explain it. State whether the acceleration is uniform or variable? Name the force responsible to cause this acceleration. What is the direction of force at any instant? Draw diagram in support of your answer.

Answer

A uniform circular motion is accelerated as the speed is same however the direction changes continuously. So, it is said to be a uniform accelerated motion.

Centripetal force is required for this acceleration and its direction is towards the centre of the circular path.

Question 6

Differentiate between uniform linear motion and a uniform circular motion.

Answer

Question 7

Name the force required for circular motion. State its direction.

Answer

Centripetal force is required for circular motion. The direction of Centripetal force is always directed towards the centre of circle.

Question 8

What is Centripetal force?

Answer

The force acting on a body moving in a circular path, in a direction towards the centre of circular path is called Centripetal force.

Question 9

Explain the motion of a planet around the sun in a circular path.

Answer

Motion of a planet around the sun in a circular path can be explained as the gravitational force of attraction on the planet by the sun. The sun provides the necessary centripetal force which is always directed towards the centre of the sun and in turn we can see the planets revolving around the sun.

Question 10

(a) How does a centripetal force differ from a centrifugal force with reference to the direction in which they act?

(b) Is centrifugal force the force of reaction of the centripetal force?

(c) Compare the magnitudes of centripetal and centrifugal force.

Answer

(a) Both the forces act in opposite direction with reference to the direction.

(b) No, centrifugal force is not the force of reaction of the centripetal force.

(c) The magnitude of centripetal and centrifugal force is 1:1

Question 11

Is centrifugal force a real force?

Answer

No the centrifugal force is a fictitious force.

Question 12

A small pebble tied at one end of a string is placed near the periphery of a circular disc, at the center of which the other end of the string is tied to a peg. The disc is rotating about an axis passing through its centre.

(a) What will be your observation when you are standing outside the disc? Explain.

(b) What will be your observation when you are standing at the centre of the disc. Explain.

Answer

(a) The pebble seems to move in a circular path when we are sitting outside the circular disc.

(b) The pebble seems to be stationary in front of us when we are standing at the centre of the disc.

Question 13

A piece of stone tied at the end of a thread is whirled in a horizontal circle with uniform speed with the help of hand.

Answer the following questions:

(a) Is the velocity of stone uniform or variable?

(b) Is the acceleration of stone uniform or variable?

(c) What is the direction of acceleration of stone at any instant?

(d) Which force provides the centripetal force required for circular motion?

(e) Name the force and its direction which acts on the hand.

Answer

(a) Velocity of stone is variable.

(b) Acceleration of stone is variable.

(c) The direction of acceleration of stone at any instance is to the centre of circular path.

(d) The frictional force provides the centripetal force.

(e) Centrifugal force acts on the hand and its direction is away from the centre.

Question 14

State two differences between the centripetal and centrifugal force.

Answer

Question 15

State whether the following statements are true or false by writing T/F against them.

(a) The earth moves around the sun with a uniform velocity.
False

(b) The motion of the moon around the earth in circular path is an accelerated motion.
True

(c) A uniform linear motion is unaccelerated, while a uniform circular motion is an accelerated motion.
True

(d) In a uniform circular motion, the speed continuously changes because the direction of the motion changes.
False

(e) A boy experiences a centrifugal force on his hand when he rotates a piece of stone tied at one end of a string, holding the other end in the hand.
False

Multiple Choice Type

Question 1

Which of the following quantity remains constant in uniform circular motion:

1. Velocity
2. Speed ✓
3. Acceleration
4. Both velocity and speed

Question 2

Centrifugal force is:

1. a real force
2. the force of reaction of centripetal force
3. a fictitious force ✓
4. directed towards the centre of circular path.