Work, Energy and Power

In vector form, work done W is written as:

1. $\vec{W} = \vec{F}.\vec{S}$
2. ${W} = \vec{F}.\vec{S}$
3. ${W} = \vec{F}$x $\vec{S}$cos θ
4. $\vec{W}$= F x S cos θ

Answer

${W} = \vec{F}.\vec{S}$

Reason — As force F and displacement S are vector quantities and work W is a scalar quantity so work is expressed as a dot product of force and displacement vectors. Hence, we get the expression : ${W} = \vec{F}.\vec{S}$

The dot product of two vectors is a scalar.

For work done to be maximum, the angle between the force and displacement should be :

1. 0°
2. 30°
3. 45°
4. 90°

Answer

0°

Reason — If the displacement is in the direction of force i.e., θ = 0°, then cos 0° = 1 and work done is maximum.

When a body moves in a circular path in a horizontal plane, the work done is :

1. Positive
2. Negative
3. Zero
4. Maximum

Answer

Zero

Reason — When a body revolves in a circular path under the influence of a force, on completing one round the displacement becomes zero, so the work done by the force is W = 0 because work done is a product of force and displacement.

When a ball m is thrown upwards to a height h, the work done by the force of gravity is:

1. mgh
2. -mgh
3. mg
4. mgh²

Answer

-mgh

Reason — When a ball m is thrown upwards to a height h, the displacement h (upwards) is opposite to the direction of force of gravity mg (downwards), so the work done by the force of gravity mg in displacement h is W = -mgh i.e., negative.

The S.I. unit of work is:

1. Joule
2. erg
3. Newton
4. dyne

Answer

Joule

Reason — The S.I. unit of work is joule. 1 joule of work is said to be done when a force of 1 newton displaces a body through a distance of 1 metre in its own direction.

A coolie A takes 1 minute to lift a load to the roof of a bus whereas coolie B take 2 minutes to lift the same load to the roof of the same bus. The work done by B is:

1. equal to work done by A
2. greater than work done by A
3. less than work done by A
4. none of the above.

Answer

equal to work done by A

Reason — From formula: ${W} = \vec{F}.\vec{S}$

Given that the distance lifted and the force applied are the same for both coolies, as they are lifting the same load to the same height (the roof of the bus) hence, the work done by both coolies is the same.

The time taken to do the work doesn't affect the amount of work done.

One horse power is equal to :

1. 1000 W
2. 500 W
3. 764 W
4. 746 W

Answer

746 W

Reason — 1 horse power = 746 W

kWh is the unit of

1. Power
2. Force
3. Energy
4. None of these

Answer

Energy

Reason — One kWh is the energy spent (or work done) by a source of power 1 kW in 1 hour.

1 Joule is equivalent to ............... erg

1. 10⁵
2. 10⁷
3. 10⁹
4. 1

Answer

10⁷

Reason — 1 Joule is equivalent to 10⁷ erg

The S.I. unit of power is

1. Watt
2. Joule
3. Nm
4. Nms

Answer

Watt

Reason — The S.I. unit of power is Watt. If 1 joule of work is said to be done in 1 second, the power spent is said to be 1 watt.

The energy of electron is 2.5 eV. When expressed in Joule, it is

1. 1.6 x 10^-19 J
2. 4.0 x 10^-19 J
3. 3.2 x 10^-19 J
4. 0

Answer

4.0 x 10^-19 J

Reason — Given, energy of electron = 2.5 eV

1 eV = 1.6 x 10 ^-19 J

Hence,

2.5 eV = 2.5 x 1.6 x 10 ^-19 = 4 x 10 ^-19 J

A block of mass 20 kg is pulled up a slope as shown in the figure given below with a constant speed by applying a force of 200 N parallel to the slope from the initial position A to the final position B. Work done in moving the block from A to B is:

1. 600 J
2. 500 J
3. 60 J
4. 200 J

Answer

600 J

Reason — Given,

Force = 200 N

Displacement = S = 3 m

As we know,

Work done = force × displacement in the direction of force

$W = F × S \\[0.5em] W = 200 \times 3 \\[0.5em] W = 600 J \\[0.5em]$

Therefore, work done is 600J.

A force F acts on a body and displaces it by a distance S in a direction at an angle θ with the direction of force.

(a) Write the expression for the work done by the force.

(b) What should be the angle between force and displacement so that the work done is (i) zero, (ii) maximum?

Answer

(a) When force acts at an angle θ to the direction of displacement then work done is

W = F × S Cos θ

(b)

(i) For work done to be zero the angle between force and displacement should be equal to 90° as cos 90° = 0

Therefore, product will also be zero.

W = F × S Cos 90° = 0

(ii) For work done to be maximum the angle between force and displacement should be equal to 0° as cos 0° = 1

Therefore, product will also be maximum.

W = F × S Cos 0° = F × S

A body is moved in a direction opposite to the direction of force acting on it. State whether the work is done by the force or work is done against the force.

Answer

When a body is moved in a direction opposite to the direction of force then work is done against the force acting on the body.

When the displacement of the body due to application of force is in a direction opposite to the force then,

θ = 180°, and

cos 180° = -1

Therefore, Work done = (-) Force x displacement of the body.

State whether work is done or not by writing yes or no, in the following cases?

(a) A man pushes a wall.

(b) A coolie stands with a box on his head for 15 min.

(c) A boy climbs up 20 stairs.

Answer

(a) No, work is not done by the man.

(b) No, work is not done by the coolie.

(c) Yes, work is done by the boy in climbing up the 20 stairs.

Explanation

(a) Work is not done by the man as on pushing the wall, it doesn't move hence, there is no displacement of the wall. Work is defined as the product of force and displacement in the direction of the force. Since there is no displacement, no work is done.

(b) Standing with a box on the head doesn't involve any displacement in the direction of the force of gravity acting on the box. The coolie is not moving the box, nor is there any vertical displacement. Therefore, no work is said to be done.

(c) When the boy climbs stairs, he exerts a force to lift his body against gravity. As he climbs, there is a vertical displacement as he moves from one step to the next. Since there is both force and displacement in the direction of the force (upward against gravity), work is done in this scenario.

Give an example when work done by the force of gravity acting on a body is zero even though the body gets displaced from its initial position.

Answer

When a coolie carrying a load moves on a horizontal platform, the force of gravity acting on him is normal to the displacement of the load i.e. the angle between force and displacement of load is 90°.

Work done by Coolie = F × S Cos 90° = F x S x 0 = 0.

Therefore, in this case work done by the force of gravity is zero even though the load gets displaced from its initial position.

A boy of mass m climbs up a stairs of vertical height h.

(a) What is the work done by the boy against the force of gravity?

(b) What would have been the work done if he uses a lift in climbing the same vertical height?

Answer

When a boy of mass m climb up stairs of vertical height h then

(a) Work done by the boy against the force of gravity is

W = FS = mgh

(b) The work done when the boy uses a lift in climbing the same vertical height

W = FS = mgh

What physical quantity does electron volt (eV) measure? How is it related to the S.I. unit of that quantity?

Answer

The energy of atomic particles is measured in electron volt (eV)

    1 eV = charge on an electron × 1 volt
⇒ 1 eV = 1.6 x 10^-19 coulomb x 1 volt
⇒ 1 eV = 1.6 x 10^-19 J

Complete the following sentence

(a) 1 J = ..... calorie.

(b) 1 kWh = ..... J.

Answer

(a) 1 J = 0.24 calorie.

(b) 1 kWh = 3.6 x 10⁶ J.

Name the physical quantity which is measured in calorie. How is it related to the S.I unit of that quantity?

Answer

The physical quantity which is measured in calorie is heat energy.

1 calorie = 4.18 joule

(a) Name the physical quantity measured in terms of horsepower.

(b) How is horsepower related to the S. I. unit of power?

Answer

(a) Power is the physical quantity measured in terms of horsepower.

(b) The relation between horsepower and S.I. unit of power is 1 horsepower = 746 watt.

Name the quantity which is measured in

(a) kWh

(b) kW

(c) Wh

(d) eV

Answer

(a) Energy is measured in kWh

(b) Power is measured in kW

(c) Energy is measured in Wh

(d) Energy is measured in eV

Is it possible that no transfer of energy takes place even when a force is applied to a body?

Answer

Yes there are cases when we will see no transfer of energy even on application of force.

Example - When a body moves in circular motion then force acts normal to the displacement of the body then there is no transfer of energy and work done is zero.

Define work. When is work said to be done by a force?

Answer

The definition of work states that when force is applied on a body and the body moves then work is said to be done.

The condition for work done is displacement of the body when force is applied.

How is the work done by a force measured when

(i) force is in direction of displacement,

(ii) force is at an angle to the direction of displacement?

Answer

(i) When force is in direction of displacement then work done is given as —

Work done = Force x displacement of the point of application of force in the direction of force.

When,

W = work done

F = force applied

S = displacement of the body then we get,

W = F × S

(ii) When force acts at an angle to the direction of displacement then work done is given as —

Work done = Force x component of displacement in the direction of force.

When,

W = work done

F = force applied

S = displacement of the body then we get,

W = F × S Cos θ

A body is acted upon by a force. State two conditions when the work done is zero.

Answer

The two conditions for the work done to be zero are,

(i) When there is no displacement of the body on application of force

i.e. S = 0 and

(ii) When displacement is normal to the direction of force

i.e. θ = 90° as cos 90° = 0

When a body moves in a circular path, how much work is done by the body? Give reason.

Answer

When a body moves in a circular path, no work is said to be done by the body as the force is directed towards the centre of circular path (the body is acted upon by the centripetal force).

At all points the displacement is along the tangent to the circular path, (i.e normal to the direction of the force).

A satellite revolves around the earth in a circular orbit. What is the work done by the satellite? Give reason.

Answer

When a satellite revolves around the earth in a circular orbit the work done is zero as force of gravity acting on satellite is perpendicular to its displacement.

A coolie X carrying a load on his head climbs up a slope and another coolie Y carrying the identical load on his head move the same distance on a frictionless horizontal platform. Who does more work? Explain the reason.

Answer

Work done is given by the formula:

W = F × S Cos θ

Coolie Y is moving the load on a frictionless horizontal platform. The force acting on the load is the force of gravity. In case of Coolie Y as the platform is horizontal so the angle between force and displacement is 90°.

Work done by Coolie Y = F × S Cos 90° = F x S x 0 = 0.

Therefore Coolie Y does zero work.

Coolie X is moving the load on a slope. Assuming the angle of slope as θ:

Work done by Coolie X = F × S Cos θ

Therefore, work done by coolie X is more than coolie Y.

The work done by a fielder when he takes a catch in a cricket match, is negative. Explain.

Answer

The work done by a fielder when he takes a catch is said to be negative as the force applied by him is in the direction opposite to the displacement of the ball.

What are the S.I. and C.G.S. units of work? How are they related? Establish the relationship.

Answer

The S.I unit of work is Joule.

C.G.S unit of work is erg.

Relation between joule and erg:

1 joule = 1N × 1m

As we know, 1 N = 10⁵ dyne and 1 m = 10² cm

Therefore,

    1 joule = 10⁵ dyne x 10² cm
⇒ 1 joule = 10⁷ dyne cm
So, 1 joule = 10⁷ erg.

State and define the S.I. unit of work.

Answer

The S.I unit of work is Joule.

1 joule of work is said to be done when a force of 1 newton displaces a body through a distance of 1 metre in its own direction.

Express joule in terms of erg.

Answer

1 joule = 1N × 1m

As we know, 1 N = 10⁵ dyne and 1 m = 10² cm

Therefore,

    1 joule = 10⁵ dyne x 10² cm
⇒ 1 joule = 10⁷ dyne cm
So, 1 joule = 10⁷ erg.

Define the term energy and state its S.I unit.

Answer

Energy is defined as the capacity to do work. The S.I unit of energy is Joule.

Define kilowatt hour. How is it related to joule?

Answer

kilowatt-hour is the energy spent (or work done) by a source of power 1 kW in 1 hour.

1 kWh = 3.6 × 10⁶ joule.

Define the term power. State its S.I. unit.

Answer

Power is defined as the rate of doing work. The S.I unit of power is watt (W)

Differentiate between work and power.

Answer

Differentiate between energy and power.

Answer

State and define the S.I unit of power.

Answer

The S.I unit of power is watt (W).
The power spent is said to be 1 watt, if 1 joule of work is done in 1 second.

Differentiate between watt and watt-hour.

Answer

The unit of power is watt (W) while the unit of work is watt-hour (Wh), since power × time = work or energy.

State the condition when the work done by a force is (i) positive, (ii) negative. Explain with the help of examples.

Answer

(i) When the displacement of the body is in the direction of force then the work done is said to be positive.

Therefore, W = F × S

Example - When a child pushes a toy table then the force applied by the child and the displacement of the table are in the same direction. So, work done is said to be positive.

(ii) When the displacement of the body is in opposite direction to the force applied then the work done is negative.

Therefore, W = – F × S

Example - When a ball is thrown upwards with a force, the balls moves to a height (h).

However, the displacement is opposite to the direction of force of gravity.

W = -mgh

A body of mass m falls through a height h. Obtain an expression for the work done by the force of gravity.

Answer

When body of mass m falls through a height (h) either vertically or on an inclined plane work is said to be done.

We know, work done is

W = F x S

However, the force of gravity on the body is F = mg acting vertically downwards and the vertical displacement in the direction of force is S = h.

Applying the values of F and S we get,

Work done by the force of gravity is

W = F x S
= m x g x h

State two factors on which power spent by a source depends. Explain your answer with examples.

Answer

The two factors on which the power spent by a source depends are :

1. The amount of work done by the source
2. The time taken by the source to do the said work.

For example:

Let us suppose a man X takes 5 minute to lift a load to the roof of a house and a man Y takes 10 minutes to lift the same load to the roof of the same house.

The work done by both the persons remain the same, but the power spent by the man X is twice the power spent by the man Y because man X does the work faster than man Y.

A body, when acted upon by a force of 20 kgf, gets displaced by 1 m. Calculate the work done by the force, when the displacement is

(i) in the direction of force,

(ii) at an angle of 60 degree with the force, and

(iii) normal to the force where g = 10Nkg^-1

Answer

Given,

Force = 20 kgf and g = 10N per kg

So,

Force = 20 x 10 = 200 N

Displacement = S = 1 m

As we know,

Work done = force × displacement in the direction of force

(i) When displacement is in the direction of force

$W = F × S \\[0.5em] W = 200 \times 1 \\[0.5em] W = 200 J \\[0.5em]$

Therefore, work done is 200J.

(ii) When displacement is at an angle of 60° with the force

$W = F × S \space cos \space \theta \\[0.5em] W = 200 \times 1 \space Cos \space 60 \\[0.5em] W = 200 \times 1 \times 0.5 \\[0.5em] W = 100 J$

Therefore, work done is 100J.

(iii) When displacement is normal to the force

$W = F × S \space cos \space \theta \\[0.5em] W = 200 \times 1 \space Cos \space 90 \degree\\[0.5em] W = 200 \times 1 \times 0 \\[0.5em] W = 0$

Therefore, work done is 0.

A boy of mass 40kg climbs up the stairs and reaches the roof at a height 8m in 5s. Calculate:

(i) The force of gravity acting on the boy,

(ii)The work done by him against gravity,

(iii)The power spent by the boy.

Take g = 10 ms^-2

Answer

Given,

m = 40 kg

h = 8 m

t = 5 s

(i) Force of gravity acting on the boy

$F = mg \\[0.5em] F = 40 \times 10 = 400N \\[0.5em]$

(ii) Work done against gravity

$W = F × S \\[0.5em] W = 400 \times 8 = 3200J \\[0.5em]$

(iii)

$\text{Power spent} = \dfrac{\text{work done}}{\text{time taken}} \\[0.5em] W = \dfrac{3200}{5} = 640 W$

A man spends 7.4 kJ energy in displacing a body by 74 m in the direction in which he applies force, in 2.5 s.

Calculate:

(i) the force applied and

(ii) the power spent (in H.P) by the man.

Answer

Given,

Work done = 7.4 kJ

S = 74 m

t = 2.5 s

(i) W = F x S

$\text{Force} = \dfrac{\text{work done}}{\text{distance}} \\[0.5em] F = \dfrac{7.4 \times 10^3}{74} \\[0.5em] \Rightarrow F = 100 N \\[0.5em]$

(ii)

$\text{Power spent} = \dfrac{\text{work done}}{\text{time taken}} \\[0.5em] P = \dfrac{7.4 \times 10^3}{2.5} \\[0.5em] \Rightarrow P = 2960 W \\[0.5em]$

We know,

$\text{1 H.P} = \text{746 W} \\[0.5em] \text{1 W}= \dfrac{1}{746} \text{ H.P} \\[0.5em] \therefore \text {2960 W} = \dfrac {2960}{746} \text{ H.P} \\[0.5em] \Rightarrow \text {2960 W} = \text{3.97 H.P}$

A weight lifter lifted a load of 200 kgf to a height of 2.5 m in 5 s.

Calculate:

(i) the work done, and

(ii) the power developed by him.

Take g = 10Nkg^-1

Answer

Given,

mass = 200kgf

height = 2.5m

time = 5s

Force = mg
= 200 x 10 = 2000N

So, we get force is equal to 2000N

(i) Work done = F x h

$W = 2000 \times 2.5 = 5000 J\\[0.5em]$

Therefore, work done is 5000 J.

(ii)

$\text{Power developed} = \dfrac{\text{work done}}{\text{time}} \\[0.5em] P = \dfrac{5000}{5} = 1000W$

Therefore, power developed by the boy 1000 W.

A machine raises a load of 750 N through a height of 16m in 5s. Calculate:

(i) the energy spent by the machine.

(ii) the power of the machine if it is 100% efficient.

Answer

Given,

Force = 750N

height or distance moved = 16 m

time = 5 s

(i) Energy spent or the work done = F x S

$W = 750 \times 16 = 12000 J \\[0.5em]$

Therefore, energy spent is equal to 12000 J

(ii)

$\text{Power spent} = \dfrac{\text{work done}}{\text{time taken}} \\[0.5em] W = \dfrac{12000}{5} = 2400 W \\[0.5em]$

Therefore, power spent is equal to 2400 W.

An electric heater of power 3 kW is used for 10 h. How much energy does it consume? Express your answer in

(i) kWh

(ii) joule.

Answer

Given,

Power of the electric heater = 3kW

Time for which the electric heater is used = 10 hours

We know,

Energy consumed = power × time

(i) Energy consumed in kWh

$\text{Energy} = 3 \times 10 \\[0.5em] \Rightarrow \text{Energy} = 30 kWh \\[0.5em]$

(ii) Energy consumed in joule.

$1 kWh = 3.6 \times 10^6 J \\[0.5em] 30 kWh = 30 \times 3.6 \times 10^6 \\[0.5em] \Rightarrow 30 kWh = 1.08 \times 10^8 J \\[0.5em]$

A water pump raises 50 litres of water through a height of 25m in 5s. Calculate the power of the pump used (assuming 100% efficiency).

(Take g = 10 N kg^-1 and density of water = 1000 kg m^-3).

Answer

Given,

Volume of water raised = 50 L and
50 L = 50 × 10^-3 m³

height = 25m

time spent = 5s

As we know,

Mass of water = Volume of water × density of water

$Mass =\dfrac{50\times 1000}{1000} = 50 Kg$

Work done in raising 50 kg water to height of 25 m is

W = mgh

Power = work done / time taken

Substituting the values we get

$\text{Power} = \dfrac{50 \times 10 \times 25}{5} = 2500W\\[0.5em]$

Therefore, power of the pump is 2500W.

A pump is used to lift 600 kg of water from a depth of 75 m in 10 s.

Calculate:

(a) The work done by the pump,

(b) The power at which the pump works, and

(c) The power rating of the pump if its efficiency is 40%. (Take g = 10m s^-2).

Answer

Given,

Mass of water = 600kg

Height to which the water has to be raised = 75 m

Time = 10 s

(a) Work done by the pump = mgh

Substituting the values we get,

$W = 600 \times 10 \times 75 \\[0.5em] \Rightarrow W = 4.5 \times 10^5 J \\[0.5em]$

(b) $\text{Power of the pump} = \dfrac{\text{work done}}{\text{time taken}}$

$\phantom{(b)\space}\Rightarrow\text{Power} = \dfrac{\text{mgh}}{\text{t}}$

Substituting the values we get,

$\text{Power} = \dfrac{600 \times 10 \times 75 }{10} = 45000 \text{ W}\\[1em] \Rightarrow \text{Power} = 45 \text{ kW} \\[1em]$

(c) $\text{Efficiency} = \dfrac{\text{useful power}}{\text{power input}}$

Given,

Efficiency = 40 %

$0.4 = \dfrac{45}{\text{input power}} \\[0.5em] \text{input power} = \dfrac{45 \times 10^3}{0.4} \\[0.5em] = 112.5 \times 10^3 \text{ W} \\[0.5em] = 112.5 \text{ kW}$

∴ Power rating of pump = 112.5 kW.

An ox can apply a maximum force of 1000N. It is taking part in a cart race and is able to pull the cart at a constant speed of 30ms^-1 while making its best effort. Calculate the power developed by the ox.

Answer

Given,

Force = 1000 N

Velocity = 30 m/s

Power = force × velocity

Power = 1000 x 30 = 30,000 W

Therefore, power developed by the ox is 30 kWh

The power of a motor is 40 kW. At what speed can the motor raise a load of 20,000 N?

Answer

Given,

Power = 40 kW

Force = 20,000 N

Power = force × velocity

Hence,

$\text{velocity} = \dfrac{\text{power}}{\text{force}} \\[0.5em] \Rightarrow \text{velocity} = \dfrac {40,000}{20,000} \\[0.5em] \Rightarrow \text{velocity} = 2 \space ms^{-1} \\[0.5em]$

Rajan exerts a force of 150 N in pulling a cart at a constant speed of 10ms^-1. Calculate the power exerted.

Answer

Power exerted by Rajan = force x velocity

Power = 150 x 10 = 1500 W

A boy weighing 350 N climbs up 30 steps, each 20 cm high in 1 minute.

Calculate:

(i) the work done, and

(ii) the power spent.

Answer

We know,
work done = Force × distance moved in direction of force
i.e. W = F × S

Given,

Force = 350 N

Distance covered in 30 steps (S)

S = 30 x 20 cm = 600cm
⇒ S = 6m

Substituting the values of F and S

$W = 350 \times 6 \\[0.5em] = 2100J \\[0.5em]$

∴ Work done by boy = 2100J

(ii)

$\text{Power developed} = \dfrac{\text{work done}}{\text{time taken}} \\[0.5em] = \dfrac{2100}{60} \\[0.5em] = 35 W \\[0.5em]$

∴ Power spent by boy = 35W

It takes 20 s for a person A of mass 50 kg to climb up the stairs, while another person B of same mass does the same in 15 s.

Compare the

(i) work done and

(ii) power developed by the persons A and B.

Answer

(i) We know that work done is a product of force and displacement and is independent of time. Hence both persons A and B will do the same amount of work.

Therefore, ratio of work done by A and B = 1:1

(ii) The power developed by the persons A and B :

We know that Power = work done / time

Work done is same by A and B

Time A took = 20 s

Time B took = 15 s

Therefore, more power is spent by B as B does the work at a faster rate.

Substituting the values in formula we get :

Power = 1 / time

${\text{Power spent by A}} : {\text{Power spent by B}} = \dfrac{15}{20} \\[0.5em] \Rightarrow {\text {Power spent by A}} : {\text {Power spent by B}} = 3 : 4 \\[0.5em]$

A boy of weighing 40 kgf climbs up a stair of 30 steps, each 20 cm high in 4 minutes and a girl weighing 30 kgf does the same in 3 minutes.

Compare :

(i) the work done by them, and

(ii) the power developed by them.

Answer

(i) We know that work done is a product of force and displacement

W = F x S = mgh

Given,

m₁ = 40 kgf
m₂ = 30 kgf
t₁ = 4 min = 4 x 60 =240 sec
t₂ = 3 min = 3 x 60 = 180 sec
h₁ = h₂ = 30 x 20 = 600 cm = 6 m

$\dfrac{\text {Work done by boy}}{\text {Work done by girl}} = \dfrac{m_1gh_1}{m_2gh_2} \\[0.5em] = \dfrac{m_1}{m_2} = \dfrac{40}{30} \\[0.5em] = \dfrac{4}{3} \\[0.5em]$

Therefore,

Work done by boy : Work done by girl = 4 : 3

(ii) The power developed —

We know that,

$\text{Power} = \dfrac{\text{work done}}{\text{time}} \\[0.5em] \dfrac{\text{Power developed by boy}}{\text{Power developed by girl}} \\[1em] = \dfrac{\dfrac{\text{work done by boy}}{\text{time taken by boy}}}{\dfrac{\text{work done by girl}}{\text{time taken by girl}}} \\[1em] = \dfrac{\dfrac{40 \times 10 \times 6}{240}}{\dfrac{30 \times 10 \times 6}{180}} \\[1em] = \dfrac{\dfrac{2400}{240}}{\dfrac{1800}{180}} \\[1em] = \dfrac{10}{10} \\[1em] = \dfrac{1}{1}$

Therefore,

Power developed by boy : Power developed by girl = 1:1

A man raises a box of mass 50kg to a height of 2m in 20s, while another man raises the same box to the same height in 50s.

(a) Compare: (i) the work done, (ii) the power developed by them.

(b) Calculate the (i) the work done, (ii) the power developed by each man.

Take g = 10N kg^-1.

Answer

(a)

(i) Work done = force x displacement

Hence, work done is same for both men as both carry 50 kg weight to a height of 2m.

Therefore,

Work done by first man : Work done by second man = 1 : 1

(ii)

Let the work done by both men be W.

$\text{Power} = \dfrac{\text{work done}}{\text{time}} \\[1em] \dfrac{\text{Power developed by Man A}}{\text{Power developed by Man B}} \\[1em] = \dfrac{\dfrac{\text{work done by Man A}}{\text{time taken by Man A}}}{\dfrac{\text{work done by Man B}}{\text{time taken by Man B}}} \\[1em] = \dfrac{\dfrac{W}{20}}{\dfrac{W}{50}} \\[1em] = \dfrac{5}{2}$

Power developed by Man A : Power developed by Man B = 5:2

(b)

(i) As we know,

W = F x S = mgh

$W = 50 \times 10 \times 2 = 1000 J \\[0.5em] \Rightarrow W = 1000 J \\[0.5em]$

(ii) Power developed by Man A

$P = \dfrac{1000}{20} \\[0.5em] \Rightarrow P = 50 W\\[0.5em]$

Power developed by Man B

$P = \dfrac{1000}{50} \\[0.5em] \Rightarrow P = 20 W\\[0.5em]$

A boy takes 3 minutes to lift a 20 litre water bucket from a 20 m deep well, while his father does it in 2 minutes.

(a) Compare:

(i) the work, and (ii) power developed by them.

(b) How much work each does?

Take density of water = 10³kg m ^-3 and g = 9.8 N kg^-1

Answer

(a)

(i) Work done = force x displacement

Work done is same for boy and father as both lift 20 litre water from 20 m deep well.

Work done by boy : Work done by father = 1:1

(ii) Comparing Power developed:

$\text{Power} = \dfrac{\text{work done}}{\text{time}} \\[0.5em] {\text {Power of boy}} : {\text {Power of father }} = \dfrac{\dfrac{W}{3}}{\dfrac{W}{2}} \\[0.5em] \Rightarrow {\text {Power developed by boy}} : {\text {Power developed by father}} = \dfrac{2}{3} \\[0.5em]$

Power developed by boy : Power developed by father = 2:3

(b) Work done = mgh

Given,

density of water = 10³kg m ^-3

To convert, density of water to mass per litre

We know,

1 litre = 1000 cm³
and
1 m³ = 10⁶ cm³

So,

$10^3\text{ kgm}^{-3} = \dfrac{1000\text{ kg}}{1\text{ m}^3} \\[1em] = \dfrac{1000\text{ kg}}{10^6 \text{ cm}^3} \\[1em] = \dfrac{1\text{ kg}}{1000\text{ cm}^3} \\[1em] = \dfrac{1\text{ kg}}{1 \text{ litre}}$

Hence,

20L of water = 20 Kg by mass

height = 20m

Now, substituting the values in the formula for work done we get

W = 20 x 9.8 x 20
= 3.92 kJ

A body at a height possesses:

1. Kinetic energy
2. Potential energy
3. Solar energy
4. Heat energy

Answer

Potential energy

Reason — When a body is at a height above the ground, it possesses potential energy due to its position relative to the Earth's surface. This potential energy arises from the gravitational force acting on the body and its position in the gravitational field.

The energy possessed by a body due to the force of attraction of earth on it is called its:

1. Rotational kinetic energy
2. Kinetic energy
3. Gravitational potential energy
4. Elastic potential energy

Answer

Gravitational potential energy

Reason — Gravitational potential energy is the energy an object possesses because of its position in a gravitational field. It arises from the gravitational force between the object and the Earth (or another massive body).

The energy possessed by a body in the deformed state due to change in its size or shape is called:

1. Rotational kinetic energy
2. Kinetic energy
3. Gravitational potential energy
4. Elastic potential energy

Answer

Elastic potential energy

Reason — When an object is deformed (stretched, compressed, or bent), it stores energy within itself due to the deformation. This energy is called elastic potential energy. It arises from the forces within the object's material that act to restore it to its original shape and size when the deforming force is removed.

According to the work energy theorem, the increase in the kinetic energy of a moving body is equal to ............... by a force acting in the direction of the moving body.

1. displacement
2. velocity
3. acceleration
4. work done

Answer

work done

Reason — According to the work energy theorem, the increase in the kinetic energy of a moving body is equal to work done by a force acting in the direction of the moving body.

A wire clamped at both ends is struck in the middle. It will possess :

1. rotational kinetic energy
2. translation kinetic energy
3. vibrational kinetic energy 
4. none of these

Answer

vibrational kinetic energy 

Reason — When a wire clamped at both ends is struck in the middle, it will vibrate back and forth. This motion results in vibrational kinetic energy, as the wire undergoes oscillations about its equilibrium position.

The wheel of a moving vehicle possesses :

1. rotational kinetic energy
2. translational kinetic energy
3. vibrational kinetic energy
4. both rotational and translational kinetic energy

Answer

both rotational and translational kinetic energy

Reason — When a vehicle is in motion, its wheels are both rotating and translating (moving in a straight line). The motion of the vehicle results in translational kinetic energy, as the vehicle moves forward. Additionally, each wheel is rotating about its axis, so it possesses rotational kinetic energy due to its spinning motion.

The velocity of a moving cart is reduced to $\dfrac{1}{3}$rd the initial velocity. Its kinetic energy is reduced by :

1. $\dfrac{1}{2}$

2. $\dfrac{1}{3}$

3. $\dfrac{1}{6}$

4. $\dfrac{1}{9}$

Answer

$\dfrac{1}{9}$

Reason — Let initial velocity be v.

Kinetic Energy at v = $\dfrac{1}{2}$ x m x v² = $\dfrac{\text{mv}^2}{2}$

Kinetic Energy at $\dfrac{\text{v}}{3}$ = $\dfrac{1}{2}$ x m x $(\dfrac{\text{v}}{3})^2$ = $\dfrac{1}{9}\Big(\dfrac{\text{mv}^2}{2}\Big)$

Hence, the kinetic energy is reduced by $\dfrac{1}{9}$

A body of mass 10 kg is moving with a velocity of 20 m/s. The mass of the body is doubled and velocity is halved. Its initial kinetic energy is:

1. 200 J
2. 4000 J
3. 2000 J
4. 1000 J

Answer

2000 J

Reason — Given,

Initial velocity = 20 m/s.

Mass = 10 kg

Kinetic Energy = $\dfrac{\text{mv}^2}{2}$

Substituting we get,

Kinetic Energy = $\dfrac{\text{10 x (20) }^2}{2}$ = $\dfrac{\text{10 x 400}}{2}$ = 2000 J

The kinetic energy K and momentum p are related as:

1. $p = \sqrt{2K}$

2. $p = \sqrt{2gK}$

3. K = $\dfrac{p^2}{2m}$

4. $K = \sqrt{2mp}$

Answer

K = $\dfrac{p^2}{2m}$

Reason — The kinetic energy K and momentum p are related as K = $\dfrac{p^2}{2m}$.

On doubling the velocity of a moving body, the quantity which gets double is:

1. acceleration
2. momentum
3. kinetic energy 
4. weight

Answer

momentum

Reason — The momentum of an object is given by the product of its mass (m) and velocity (v) represented by :

p = mv

If the velocity is doubled, then the new momentum (p') becomes:

p' = m x 2v = 2(mv) = 2p

So, the momentum gets doubled when the velocity is doubled.

In a photoelectric cell, the change in energy is from:

1. electrical to mechanical
2. light energy to electrical energy
3. electrical energy to light energy
4. chemical energy to light energy

Answer

light energy to electrical energy

Reason — A photoelectric cell, also known as solar cell, converts light energy (photons) into electrical energy (electrons). When light strikes the surface of the cell, it excites electrons, causing them to be ejected from the material (the photoelectric effect). These ejected electrons can then be collected and used as electric current.

In a petrol vehicle while in motion, the change in energy is from

1. kinetic energy to potential energy
2. chemical energy to kinetic energy
3. potential energy to kinetic energy 
4. chemical energy to potential energy

Answer

chemical energy to kinetic energy

Reason — In a petrol vehicle, the chemical energy stored in the fuel (petrol) is converted into kinetic energy as the vehicle moves. This conversion of chemical energy into kinetic energy occurs through the process of combustion within the engine, where the chemical bonds in the fuel are broken, releasing energy that propels the vehicle forward.

In nuclear fission:

1. chemical energy changes to electrical energy
2. mechanical energy changes to chemical energy
3. nuclear energy changes to electrical energy
4. electric energy changes to nuclear energy

Answer

nuclear energy changes to electrical energy

Reason — Nuclear fission is a nuclear reaction in which the nucleus of an atom splits into smaller parts, releasing a significant amount of energy. This energy is in the form of nuclear energy and is used for constructive purposes to produce electrical energy.

In an electric cell while in use, the change in energy is from:

1. electrical to mechanical
2. electrical to chemical
3. chemical to mechanical
4. chemical to electrical

Answer

chemical to electrical

Reason — An electric cell, such as a battery, converts chemical energy stored within it into electrical energy when in use. The chemical reactions occurring within the battery cause a flow of electrons, generating an electric current.

What are the two forms of mechanical energy?

Answer

The two forms of mechanical energy are

1. Kinetic energy
2. Potential energy

Name the form of energy which a wound-up watch spring possesses.

Answer

Wound up watch spring possesses an elastic potential energy.

Name the type of energy (kinetic energy K or potential energy U) possessed in the following cases:

(a) A moving cricket ball

(b) A compressed spring

(c) A moving bus

(d) A stretched wire

(e) An arrow shot out of a bow.

(f) A piece of stone placed on the roof.

Answer

(a) A moving cricket ball posses Kinetic energy — K.

(b) A compressed spring posses Potential energy — U.

(c) A moving bus posses Kinetic energy — K.

(d) A stretched wire posses Potential energy — U.

(e) An arrow shot out of a bow posses Kinetic energy — K.

(f) A piece of stone placed on the roof posses Potential energy — U.

(a) A body of mass m is moving with a velocity v. Write the expression for its kinetic energy.

(b) Show that the quantity 2K/v² has the unit of mass, where K is the kinetic energy of the body.

Answer

(a) The expression for a body of mass m moving with a velocity v is given by

${\text {Kinetic energy} = \dfrac{1}{2} \times m \times velocity^2} \\[0.5em] {\text {Kinetic energy} = \dfrac{1}{2} \times m \times v^2} \\[0.5em]$

(b) 2K / v² = Joules / (ms^-1)² = kg

So, Kg is the unit of mass

Two bodies A and B of masses m and M (M ≫ m) have same kinetic energy. Which body will have more momentum?

Answer

Kinetic energy and momentum are related as

$p = \sqrt{2mk}$

Since,

the kinetic energy of both bodies are same, momentum is directly proportional to the square root of mass.

As we can see that mass of body B is greater than that a body A.

Therefore, body B will have more momentum than body A.

Complete the following sentences

(a) The kinetic energy of a body is the energy by virtue of its ...............

(b) The potential energy of a body is the energy by virtue of its ...............

Answer

(a) The kinetic energy of a body is the energy by virtue of its motion.

(b) The potential energy of a body is the energy by virtue of its position.

Name the form of energy in which potential energy can change.

Answer

The potential energy can change only in the form of kinetic energy.

Name the form of mechanical energy, which is put to use.

Answer

Kinetic energy is put to use in the form of mechanical energy.

Energy can exist in several forms and may change from one form to another. For each of the following, state the energy changes that occur in:

(a) the unwinding of a watch spring

(b) a loaded truck when started and set in motion

(c) a car going uphill

(d) photosynthesis in green leaves

(e) charging of a battery

(f) respiration

(g) burning of a match stick

(h) explosion of crackers

Answer

(a) Potential energy of a watch spring converts into kinetic energy

(b) Chemical energy of diesel or petrol converts into mechanical energy

(c) Kinetic energy converts into potential energy

(d) Light energy converts into chemical energy

(e) Electrical energy converts into chemical energy

(f) Chemical energy converts into heat energy

(g) Chemical energy converts into heat and light energy

(h) Chemical energy converts into heat, light and sound energy

State the energy changes in the following cases while in use:

(a) Loudspeaker

(b) A steam engine

(c) Microphone

(d) Washing machine

(e) A glowing electric bulb

(f) Burning coal

(g) A solar cell

(h) Biogas burner

(i) An electric cell in a circuit

(j) A petrol engine of a running car

(k) An electric iron

(l) A ceiling fan

(m) An electromagnet.

Answer

(a) Electrical energy changes into sound energy

(b) Heat energy changes into mechanical energy

(c) Sound energy changes into electrical energy

(d) Electrical energy changes into mechanical energy

(e) Electrical energy changes into light energy

(f) Chemical energy changes into heat energy

(g) Light energy changes into electrical energy

(h) Chemical energy changes into heat energy

(i) Chemical energy changes into electrical energy

(j) Chemical energy changes into mechanical energy

(k) Electrical energy changes into heat energy

(l) Electrical energy changes into mechanical energy

(m) Electrical energy changes into magnetic energy

Name the process used for producing electricity from nuclear energy.

Answer

Nuclear fission is the process used for producing electricity from nuclear energy.

Is it practically possible to convert a form of energy completely into the other useful form? Explain your answer.

Answer

It is not possible to completely convert one form of energy into other as a part of the energy is dissipated in the form of heat which is lost to the surroundings.

Complete the following sentence

The conversion of part of energy into an undesirable form is called ...............

Answer

The conversion of part of energy into an undesirable form is called degradation of energy

Define the term potential energy of a body. Name its two forms and give one example of each.

Answer

The energy possessed by a body at rest due to its position or size and shape is called the potential energy.

Different forms of potential energy are as follows:

(i) Gravitational potential energy — It is the energy possessed by a body due to the force of attraction of the earth.

Example — A stone at a height has gravitational potential energy.

(ii) Elastic potential energy — It is the energy possessed by a body due to the deformed state because of change in its shape and size.

Example — When a spring is compressed it has elastic potential energy.

Name the form of energy which a body may possess even when it is not in motion. Give an example to support your answer.

Answer

A body possesses potential energy even when it is not in motion.

For example — a stone raised at a height has gravitational potential energy.

Write an expression for the potential energy of a body of mass m placed at a height h above the earth’s surface. State the assumptions made, if any.

Answer

The work done in lifting a body to a height h is

W = force of gravity (mg) × displacement (h) = mgh

Therefore, this work is stored in the body in the form of its gravitational potential energy.

Hence, Gravitational potential energy U = mgh

What do you understand by the kinetic energy of a body?

Answer

Kinetic Energy of a body is the energy possessed by a body in motion.

State the work–energy theorem.

Answer

According to the work theorem,

The work done by a force in the same direction on a moving body is equal to the increase in its kinetic energy.

A body of mass m is moving with a uniform velocity u. A force is applied on the body due to which its velocity increases from u to v. How much work is being done by the force?

Answer

Mass = m

Change in velocity from u to v, so acceleration acts (a)

Force = f

Work done by the force = force × displacement

From equation of motion we know,

$v^2 = u^2 + 2aS \\[0.5em] \therefore S = \dfrac{v^2 -u^2}{2a}$

Substituting it in the formula for work done:

$W = m \times a \times (\dfrac{v^2-u^2}{2a}) \\[0.5em] W = (\dfrac{1}{2} \times m \times v^2) - (\dfrac{1}{2} \times m \times u^2) \\[0.5em] W = (\dfrac{1}{2} \times m \times v^2) - (\dfrac{1}{2} \times m \times u^2) \\[0.5em] W = \dfrac{1}{2} m (v^2 - u^2) \\[0.5em] W = KE_f - KE_i$

A light mass and a heavy mass have equal momentum. Which will have more kinetic energy?

Answer

Kinetic energy (KE) and momentum (p) are related as

$KE = \dfrac{p^2}{2m} \\[0.5em]$

As both masses have the same momentum p. The kinetic energy k is inversely proportional to the mass of the body.

Hence, a body of light mass has more kinetic energy as smaller the mass, larger is its kinetic energy.

Name the three forms of kinetic energy and give one example of each.

Answer

The three forms of kinetic energy are:

(i) Vibrational kinetic energy

Example — A wire clamped at both the ends vibrates when struck.

(ii) Rotational kinetic energy

Example — A spinning top.

(iii) Translational kinetic energy

Example — A car moving in a straight path.

State two differences between the potential energy and the kinetic energy.

Answer

Name six different forms of energy?

Answer

The six different forms of energy are

(i) Heat energy

(ii) Solar energy

(iii) Nuclear energy

(iv) Hydro energy

(v) Light energy

(vi) Mechanical energy

What is degraded energy?

Answer

While transforming energy from one from to another desired form, the entire energy does not change into the desired form. A part of energy changes either to some other undesirable form (usually heat due to friction) or a part is lost to the surroundings due to radiation and becomes useless. This conversion of energy to the undesirable form is called dissipation of energy.

Since, this part of energy is not available to us for any productive purpose so we call this part of energy as degraded energy.

What do you mean by degradation of energy? Explain it by taking one example of your daily life.

Answer

While transforming energy from one from to another desired form, the entire energy does not change into the desired form. A part of energy changes either to some other undesirable form (usually heat due to friction) or a part is lost to the surroundings due to radiation and becomes useless. This conversion of energy to the undesirable form is called dissipation of energy or degradation of energy.

Since, this part of energy is not available to us for any productive purpose so we call this part of energy as degraded energy.

Example — When a vehicle is run by using the chemical energy of its fuel a major part is wasted as heat and sound. Only a part of it is changed into useful mechanical energy.

What is meant by gravitational potential energy? Derive an expression for it for a body placed at a height above the ground.

Answer

The potential energy possessed by a body due to the force of attraction of the earth on it, is called the gravitational potential energy.

When a body is placed at a height above the ground then the amount of work done in lifting the body to that height against the force of gravity is called the gravitational potential energy.

When we lift a body of mass m from the ground to a height h.Then, force of gravity (mg) acts on the body acting vertically downward which must be equal to the least upward force F required to lift the body.

Work done = force of gravity (mg) × displacement (h)

⇒ W = mgh

So, the work done on the body is stored in the form of its gravitational potential energy when it is at a height h.

Hence,

Gravitational potential energy U = mgh.

When an arrow is shot from a bow, it has kinetic energy in it. Explain briefly from where does it get its kinetic energy?

Answer

When the string of a bow is pulled, the work done is stored in the form of elastic potential energy.

When the string is released to shoot the arrow, the potential energy of the bow changes into the kinetic energy.

The kinetic energy is the same potential energy stored when the string was pulled.

A ball is placed on a compressed spring. What form of energy does the spring possess? On releasing the spring, the ball flies away. Give a reason.

Answer

When the ball is placed on a compressed spring, the compressed spring has elastic potential energy.

The potential energy of the spring changes into kinetic energy when it is released and as a result it flies.

A pebble is thrown up. It goes to a height and then comes back on the ground. State the different changes in the form of energy during its motion.

Answer

On being thrown upwards, the kinetic energy of the pebble changes to potential energy.

Its kinetic energy is completely converted into potential energy when the pebble reaches its maximum height.

The potential energy is then converted into kinetic energy while coming down and the potential energy is completely converted to kinetic energy when the pebble reaches the ground.

In what way does the temperature of water at the bottom of a waterfall differ from the temperature at the top? Explain the reason.

Answer

When the water falls from the height, the potential energy stored in water at a height changes into the kinetic energy.

On reaching the ground, a part of the kinetic energy of water changes into the heat energy which increases the temperature of the water.

Two bodies of equal masses are placed at heights h and 2h. Find the ratio of their gravitational potential energies.

Answer

Given,

Mass of body A and body B = m each

Height H_A = h

Height H_B = 2h

We know, Gravitational potential energy = mgh

Substituting the values we get,

$\text {Ratio of gravitational P.E.} = \dfrac{mgh}{mg2h} \\[0.5em] \Rightarrow \text {Ratio of gravitational P.E.} = \dfrac{1}{2} \\[0.5em]$

Hence, ratio of gravitational potential energies of the two bodies = 1 : 2

Find the gravitational potential energy of 1 kg mass kept at a height of 5m above the ground. Calculate its kinetic energy when it falls and hits the ground. Take g = 10ms^-2.

Answer

Given,

Mass, m = 1 kg

Height, h = 5 m

Gravitational potential energy = mgh
= 1 × 10 × 5
= 50 J

When the mass hits the ground, its entire Potential energy is converted to Kinetic energy.

Hence, Kinetic energy of mass on hitting the ground = 50 J.

A box of mass 300 kg has gravitational potential energy stored in it equal to 29400 J. Find the height of the box above the ground.

(Take g = 9.8 N kg^-1)

Answer

Given,

Mass of box = 300 Kg

Gravitational potential energy = 29400 J

We know,

Gravitational potential energy = mgh

Therefore,

$h = \dfrac{\text{Gravitational P.E.}}{\text{mass} \times \text{gravity}}$

Substituting the values in formula we get,

$\text{height} = \dfrac{29400}{300 \times 9.8} \\[1em] \Rightarrow \text{height} = \dfrac{29400}{2940} \\[1em] \Rightarrow \text{height} = 10\text{ m}$

A body of mass 10 kg falls from a height of 20 m to 8 m.

Calculate:

(i) the loss in potential energy of the body,

(ii) the total energy possessed by the body at any instant? (Take g = 10 ms^-2).

Answer

Given,

Mass = 10Kg

Fall in height = 20 - 8 = 12m

(i) Loss in potential energy = mg(h₁ - h₂)

Substituting the vales in formula we get,

Loss in potential energy = 10 x 10 x 12 = 1200 J

(ii) Total energy remains constant for free fall.

Total energy = P.E + K.E

So, at height 20 m, K.E = 0

Therefore total energy = P.E + K.E

Total energy = mgh + 0
= 10 x 10 x 20 = 2000 J

Calculate the height through which a body of mass 0.5 kg is lifted if the energy spent in doing so is 1.0 J. Take g = 10ms^-2.

Answer

Given,

Mass = 0.5 kg

Energy = 1 J

We know that,

$\text{Gravitational P.E.} = \text{mgh} \\[0.75em] \therefore h = \dfrac{\text{Gravitational P.E.}}{\text{mg}} \\[0.5em]$

Substituting the values we get,

$h = \dfrac{1}{0.5 \times 10} \\[0.5em] \Rightarrow h = 0.2m \\[0.5em]$

A boy weighing 50 kgf climbs up from the first floor at a height of 3 m above the ground to the third floor at a height of 9 m above the ground. What will be the increase in his gravitational potential energy?

(Take g = 10 N kg^-1).

Answer

Mass = 50 Kgf

Increase in gravitational potential energy = mg(h₂ – h₁)

= 50 x 10 x (9 - 3)

= 50 x 10 x 6

= 3000 J

A vessel containing 50 kg of water is placed at a height 15m above the ground. Assuming the gravitational potential energy at the ground to be zero, what will be the gravitational potential energy of water in the vessel?

(g = 10ms^-2).

Answer

Given,

Mass = 50 kg

Height = 15 m

Gravitational potential energy = mgh

Substituting the values we get,

$\text {Gravitational P.E.} = 05 \times 10 \times 15 \\[0.5em] \Rightarrow \text {Increase in gravitational P.E.} = 7500J \\[0.5em]$

A man of mass 50 kg climbs up a ladder of height 15m.

Calculate:

(i) the work done by the man,

(ii) the increase in his potential energy.

(g = 9.8 m s^-2).

Answer

Given,

Mass = 50 kg

h₁ = 0 m

h₂ = 15 m

(i) Work done by man = mgh₂

Substituting the values we get,

W = 50 x 9.8 x 15 = 7350 J

(ii) Increase in his potential energy = Mg (h₂ – h₁)

= 50 x 9.8 x (15 - 0)

= 7350 J

A block A, whose weight is 100N, is pulled up a slope of length 5m by means of a constant force F (=100N) as illustrated.

(a) What is the work done by the force F in moving the block A, 5m along the slope?

(b) What is the increase in potential energy of the block A?

(c) Account for the difference in the work done by the force and the increase in potential energy of the block.

Answer

Given,

F = 100 N

h = 3m

displacement = 5m

We know,

(i) Work done = Force × displacement in the direction of the force

$W = 100 \times 5 \\[0.5em] \Rightarrow W = 500 J \\[0.5em]$

(ii) The potential energy gained by the block U = mgh

$\text{P.E.} = 100 \times 3 \\[0.5em] \Rightarrow \text { P.E. gained by the block}= 300 J \\[0.5em]$

(iii) The difference (200 J) energy is used in doing work against the force of friction between the block and the slope and it will appear as heat energy.

Find the kinetic energy of a body of mass 5 kg moving with a uniform velocity of 10 m s^-1.

Answer

Given,

m = 5 kg

Velocity, v = 10 m / s

Kinetic energy = $\dfrac{1}{2}$ × mass × (velocity)²

Substituting the values we get,

KE = $\dfrac{1}{2}$ x 5 x 10² = 250 J

If the speed of a car is halved, how does its kinetic energy change?

Answer

Let speed of car be v.

Kinetic Energy at speed v = $\dfrac{1}{2}$ x m x v² = $\dfrac{\text{mv}^2}{2}$

Kinetic Energy at speed $\dfrac{\text{v}}{2}$ = $\dfrac{1}{2}$ x m x $(\dfrac{\text{v}}{2})^2$ = $\dfrac{\text{mv}^2}{8}$ = $\dfrac{1}{4}\Big(\dfrac{\text{mv}^2}{2}\Big)$

Hence, when the speed of the car is halved the kinetic energy becomes one-fourth.

Two bodies of equal masses are moving with uniform velocities v and 2v. Find the ratio of their kinetic energies.

Answer

Given,

Velocity of first body v₁ = v

Velocity of second body, v₂ = 2v

As the mass of the two bodies are same and as kinetic energy is directly proportional to the square of the velocity (K α v²)

Hence, ratio of their kinetic energies is

$\dfrac{K_1}{K_2} = \dfrac{(v_1)^2}{(v_2)^2} \\[0.5em] \dfrac{K_1}{K_2} = \dfrac{v^2}{(2v)^2} \\[0.5em] \dfrac{K_1}{K_2} = \dfrac{v^2}{4v^2} \\[0.5em] \dfrac{K_1}{K_2} = \dfrac{1}{4} \\[0.5em]$

Two bodies have masses in the ratio 5 : 1 and kinetic energies in the ration 125 : 9. Calculate the ratio of their velocities.

Answer

We know that,

$\text{K.E.} = \dfrac{1}{2} \times m \times v^2 \\[0.5em]$

Let the two bodies be A and B.

Let mass of body A be m_A and body B be m_B. Let velocity of body A be v_A and body B be v_B.

Given,

Ratio of masses:

$\dfrac {m_A}{m_B} = \dfrac {5}{1} \\[0.5em]$

Ratio of K.E.:

$\dfrac {KE_A}{KE_B} = \dfrac {125}{9} \\[1em] \dfrac {KE_A}{KE_B} = \dfrac{\dfrac{1}{2} \times m_A \times v_A^2}{\dfrac{1}{2} \times m_B \times v_B^2} \\[0.5em] \Rightarrow \dfrac {125}{9} = \dfrac{\dfrac{1}{2} \times m_A \times v_A^2}{\dfrac{1}{2} \times m_B \times v_B^2} \\[0.5em] \Rightarrow \dfrac {125}{9} = \dfrac{m_A}{m_B} \times \Big(\dfrac{v_A}{v_B}\Big)^2 \\[0.5em] \Rightarrow \dfrac {125}{9} = \dfrac{5}{1} \times \Big(\dfrac{v_A}{v_B}\Big)^2 \\[0.5em] \Rightarrow \Big(\dfrac{v_A}{v_B}\Big)^2 = \dfrac{125}{9} \times \dfrac{1}{5} \\[0.5em] \Rightarrow \Big(\dfrac{v_A}{v_B}\Big)^2 = \dfrac{25}{9} \\[0.5em] \Rightarrow \dfrac{v_A}{v_B} = \sqrt{\dfrac{25}{9}} \\[0.5em] \Rightarrow \dfrac{v_A}{v_B} = \dfrac{5}{3} \\[0.5em]$

∴ Ratio of their velocities = 5:3

A car is running at a speed of 15 km h^-1 while another similar car is moving at a speed of 45 km h^-1. Find the ratio of their kinetic energies.

Answer

We know that,

$KE =\dfrac{1}{2} \times m \times v^2 \\[0.5em]$

Hence, KE α v²

So we get,

$\dfrac{KE_1}{KE_2} = \dfrac{v_1^2}{v_2^2} \\[0.5em] \dfrac{KE_1}{KE_2} = (\dfrac{15}{45})^2 \\[0.5em] \dfrac{KE_1}{KE_2} = (\dfrac{1}{3})^2 \\[0.5em] \Rightarrow \dfrac{KE_1}{KE_2} = (\dfrac{1}{9}) \\[0.5em]$

A ball of mass 0.5 kg slows down from a speed of 10ms^-1 to that of 6ms^-1. Calculate the change in kinetic energy of the ball.

Answer

Given,

Mass = 0.5 kg

Initial velocity = 10 m / s

Final velocity of the ball = 6 m / s

Kinetic energy = $\dfrac{1}{2}$ × mass × (velocity)²

Substituting the values in the equation we get,

Initial KE = $\dfrac{1}{2}$ x 0.5 x 10²

= $\dfrac{1}{2}$ x 0.5 x 100

= 0.5 x 50

= 25 J

Final KE = $\dfrac{1}{2}$ x 0.5 x 6²

= $\dfrac{1}{2}$ x 0.5 x 36

= 0.5 x 18

= 9 J

So, change in the kinetic energy of the ball = 9 J - 25 J = -16J

Hence, there is a decrease in the kinetic energy of the ball by 16J.

A canon ball of mass 500g is fired with a speed of 15m/s^-1.

Find:

(i) its kinetic energy and

(ii) its momentum.

Answer

Given,

mass = 500 g = 0.5 kg

Speed = v = 15 m / s

(a) We know,

Kinetic energy = 1 / 2 × mass × (velocity)²

Substituting the values in the equation we get,

$KE = \dfrac{1}{2} \times 0.5 \times 15^2 \\[0.5em] KE = \dfrac{1}{2} \times 0.5 \times 225 \\[0.5em] \Rightarrow KE = 56.25J \\[0.5em]$

(b) We know,

Momentum = mass × velocity

Substituting the values in the equation we get,

Momentum = 0.5 x 15
= 7.5 kgm/s

A body of mass 10 kg is moving with a velocity 20 m s^-1.

If the mass of the body is doubled and its velocity is halved,

find:

(i) the initial kinetic energy, and

(ii) the final kinetic energy.

Answer

Given,

Initial Mass = 10 kg and

Final mass = 2 × 10 kg = 20kg

Initial Velocity = 20 m / s

Changed velocity v2 = 20 / 2 = 10 m / s

(i) Initial kinetic energy = 1 / 2 × mass × (velocity)²

$\text {Initial Kinetic Energy} = \dfrac{1}{2} \times 10 \times (20)^2 \\[0.5em] \Rightarrow \text{Initial kinetic energy} = 2000J \\[0.5em]$

(ii) Final kinetic energy

$\text {Final Kinetic Energy} = \dfrac{1}{2} \times 20 \times (10)^2 \\[0.5em] \Rightarrow \text{Final kinetic energy} = 1000J \\[0.5em]$

A truck weighing 1000 kg changes its speed from 36 km/h to 72 km/h in 2 minutes.

Calculate:

(i) the work done by the engine and

(ii) its power.

(g =10 m/ s^-2)

Answer

Given,

Mass = 1000 kg

$\text {Initial velocity (u) } = 36 km / h \\[0.5em] = \dfrac {36 \times 1000m}{3600s} \\[0.5em] \Rightarrow \text {Initial velocity (u) } = 10ms^{-1} \\[0.5em]$

$\text {Final velocity (v) } = 72 km / h \\[0.5em] = \dfrac {72 \times 1000m}{3600s} \\[0.5em] \Rightarrow \text {Final velocity (v) } = 20ms^{-1} \\[0.5em]$

From, equation of motion we get

$S = ( v^2 - u^2) / time \\[0.5em]$

(i) Work done = force x displacement

$W = \dfrac{1000 \times (20^2 -10^2)}{2} \\[0.5em] W = \dfrac{1000 \times (400 -100)}{2} \\[0.5em] W = 500 \times 300 \\[0.5em] \Rightarrow W = 150000J = 1.5 × 10^5J \\[0.5em]$

(ii) Power = work done / time taken

$Power = \dfrac{1.5 \times 10^5}{120} \\[0.5em] \Rightarrow Power = 1.25 × 10^3 W$

A body of mass 60 kg has the momentum of 3000 kgms^-1.

Calculate:

(i) the kinetic energy and

(ii) the speed of the body.

Answer

Given,

Mass = 60 kg

Momentum = 3000 kgm / s

(a)

$\text{Kinetic Energy} = \dfrac{\text{momentum}^2}{2 \times \text{mass}} \\[0.5em] \Rightarrow \text{KE} = \dfrac{3000^2}{2 \times 60} \\[0.5em] \Rightarrow \text{KE} = \dfrac{3000 \times 3000}{120} \\[0.5em] \Rightarrow \text{KE} = 75000\text{ J} = 7.5 × 10^4\text{ J}$

(b)

$\text{Momentum} = \text{Mass} \times \text{Velocity} \\[0.5em] \Rightarrow \text{Velocity} = \dfrac{\text{Momentum}}{\text{Mass}} \\[0.5em] \Rightarrow \text{Velocity} = \dfrac{3000}{60} \\[0.5em] \Rightarrow \text{Velocity} = 50\text{ ms}^{-1}$

How much work is needed to be done on a ball of mass 50g to give it a momentum of 5 kg m s^-1?

Answer

Given,

mass = 50gm = 0.05kg

momentum = 500 gcm / s = 0.005 kgm / s

KE = momentum² / 2 x mass

$\text{Work done} = KE = \dfrac {momentum^2}{2 \times mass} \\[0.5em] \text{Work done} = KE = \dfrac{0.005^2} {2 \times 0.05} \\[0.5em] \Rightarrow KE =250 J \\[0.5em]$

How much energy is gained by a box of mass 20 kg when a man

(a) carrying the box waits for 5 minutes for a bus?

(b) runs carrying the box with a speed of 3 ms^-1 to catch the bus?

(c) raises the box by 0.5 m in order to place it inside the bus?

(g=10 ms^-2)

Answer

Given,

Mass = 20 kg

(a) As there is no displacement of the man, so work done is Zero.

(b) We know,

Work done = Kinetic energy of man = 1 / 2 × mass × (velocity)²

$\text{Work done} = \text{Kinetic energy of man} \\[0.5em] = \dfrac{1}{2} \times \text{mass} \times \text{velocity}^2 \\[0.5em] = \dfrac{1}{2} \times 20 \times 3^2 \\[0.5em] = \dfrac{1}{2} \times 20 \times 9 \\[0.5em] = 90 J \\[0.5em]$

∴ Energy Gained = 90 J

(c) We know,

Potential energy = mgh

$\text{PE} = 20 \times 10 \times 0.5 \\[0.5em] \Rightarrow U = 100 J \\[0.5em]$

A bullet of mass 50g is moving with a velocity of 500ms^-1. It penetrates 10 cm into a still target and comes to rest.

Calculate:

(a) the kinetic energy possessed by the bullet, and

(b) the average retarding force offered by the target.

Answer

Given,

Mass = 50 g = 0.05 kg

Velocity = 500 m / s

Distance (S) = 10 cm = 0.1 m

(a) The kinetic energy possessed by the bullet = $\dfrac{1}{2}$ × mass × (velocity)²

Substituting the values in equation we get,

$KE = \dfrac {1}{2} \times 0.05 \times 500^2 \\[0.5em] KE = \dfrac {1}{2} \times 0.05 \times 250000 \\[0.5em] \Rightarrow KE = 6250J \\[0.5em]$

(b)

$\text{Retarding Force} = \dfrac{\text{Work done by bullet}}{\text{distance}} \\[0.5em] = \dfrac{6250}{0.1} \\[0.5em] = 62500N \\[0.5em]$

∴ Average retarding force offered by target = 62500N

A spring is kept compressed by a small trolley of mass 0.5 kg lying on a smooth horizontal surface as shown. When the trolley is released, it is found to move at a speed of v = 2 ms^-1. What potential energy did the spring possess when compressed?

Answer

Given,

Mass = 0.5 kg

Velocity = 2 m / s

Potential Energy possessed by the spring is equal to the kinetic energy of moving trolley.

Kinetic energy of trolley

$= \dfrac{1}{2} \times \text{mass} \times \text{velocity}^2 \\[0.5em] = \dfrac{1}{2} \times 0.5 \times 2^2 \\[0.5em] = \dfrac{1}{2} \times 0.5 \times 2^2 \\[0.5em] = 1 \text{ J} \\[0.5em]$

∴ Potential energy = Kinetic energy = 1.0 J

According to the principle of conservation of mechanical energy :

1. Potential energy of a system is always greater than its kinetic energy
2. Kinetic energy of a system is always greater than its potential energy
3. Mechanical energy is always converted into heat energy
4. Total mechanical energy of a system remains constant if no external force is worked on it.

Answer

Total mechanical energy of a system remains constant if no external force is worked on it.

Reason — The conservation of mechanical energy states that the total mechanical energy (sum of kinetic energy and potential energy) of a system remains constant if no external forces, such as friction or air resistance, are acting on it.

A skater is gliding on a smooth ice surface. What happens to his mechanical energy as he skates?

1. It increases
2. It decreases
3. It becomes zero
4. It remains constant

Answer

It remains constant

Reason — As the skater glides across the ice, he possess kinetic energy due to his movement. The potential energy remains constant as there is no significant change in height. Assuming a smooth ice surface with no friction or air resistance, the external forces are absent, hence, according to the principle of conservation of mechanical energy, the total mechanical energy (KE + PE) of the skater remains constant.

A spring is compressed storing potential energy. When the spring is released it propels an object forward. What change would you notice in the total mechanical energy of the system?

1. It increases
2. It decreases
3. It becomes zero
4. It remains constant

Answer

It remains constant

Reason — When the spring is compressed, it stores potential energy. Upon release, this potential energy is converted into kinetic energy as the spring propels an object forward. Assuming there are no significant external forces acting on the system (such as friction), the total mechanical energy of the system remains constant.

When a car is moving on a level road and breaks are applied till it comes to rest, what happens to its mechanical energy?

1. It increases
2. It decreases
3. It becomes zero
4. It becomes negative

Answer

It decreases

Reason — When the brakes are applied, the car experiences friction between the brake pads and the wheels. This friction converts the kinetic energy of the car into other forms of energy, such as heat and sound. As the car eventually comes to rest, its velocity becomes zero, and thus its kinetic energy becomes zero. Therefore, the kinetic energy component of the car's mechanical energy decreases to zero. As the height above the ground does not change significantly so, the potential energy component remains relatively constant. Hence, mechanical energy (KE + PE) decreases.

A ball of mass m is thrown vertically up with an initial velocity so as to reach a height h. The correct statement is:

1. Potential energy of the ball at the ground is mgh.
2. Kinetic energy of the ball at the ground is zero.
3. Kinetic energy of the ball at the highest point is mgh.
4. Potential energy of the ball at the highest point is mgh.

Answer

Potential energy of the ball at the highest point is mgh.

Reason — At the highest point, the ball has maximum potential energy. The potential energy at a height h, above the ground is given by the formula mgh.

A a body is released from a height. During its motion in striking the ground, the quantity which does not change is:

1. momentum
2. kinetic energy
3. potential energy
4. mechanical energy

Answer

mechanical energy

Reason — Mechanical energy, which is the sum of kinetic and potential energy, remains constant during the motion of the body. Initially, when the body is released from a height, it has potential energy. As it falls, this potential energy decreases while its kinetic energy increases. However, the sum of kinetic and potential energy (mechanical energy) remains constant in the absence of external forces like air resistance.

A pendulum is oscillating on either side of its rest position. The correct statement is :

1. It has only the kinetic energy at its each position.
2. It has the maximum kinetic energy at its extreme position.
3. It has the maximum potential energy at its mean position.
4. The sum of its kinetic energy and potential energy remains constant throughout the motion.

Answer

The sum of its kinetic and potential energy remains constant throughout the motion.

Reason — The sum of kinetic and potential energy does not remain constant throughout the motion of a pendulum. It varies as the pendulum swings due to the interconversion of kinetic and potential energy. However, the sum of kinetic and potential energy is constant if we consider the entire system (kinetic energy + potential energy = mechanical energy), as long as there are no external forces like friction acting on the pendulum.

A simple pendulum while oscillating rises to a maximum vertical height of 7 cm from its rest position where it reaches its extreme position on one side. The mass of the bob of simple pendulum is 400 g and g = 10 m/s². The total energy of the simple pendulum at any instant while oscillating is:

1. 0.28 J
2. 2.8 J
3. 28 J 
4. 28000 J

Answer

0.28 J

Reason — Given,

m = 400 g = 0.4 kg

g = 10 m/s²

h = 7 cm = 0.07 m

The potential energy of the pendulum at its extreme position (maximum height) is : mgh

and kinetic energy at this point = 0

Substituting we get,

Total energy = PE + KE = mgh + 0 = (0.4 x 10 x 0.07) + 0 = 0.28 J

A body is thrown vertically upwards. Its velocity keeps on decreasing. What happens to its kinetic energy as its velocity becomes zero?

Answer

When a body is thrown vertically upwards, its kinetic energy changes into potential energy and its velocity becomes zero.

A body falls freely under gravity from rest. Name the kind of energy it will possess

(a) At the point from where it falls.

(b) While falling

(c) On reaching the ground.

Answer

(a) The energy possessed at the point from where it falls is potential energy.

(b) Potential energy and kinetic energy, both are possessed at the time of fall.

(c) The energy possessed by the body on reaching the ground is kinetic.

State the principle of conservation of energy.

Answer

The principle of conservation of energy states that energy can neither be created nor can be destroyed. It only changes from one form to other.

What do you understand by the conservation of mechanical energy? State the condition under which the mechanical energy is conserved.

Answer

Whenever there is an interchange between the potential energy and kinetic energy, the total mechanical energy remains constant. This is principle of conservation of mechanical energy.

i.e K + U = constant provided there are no frictional forces.

The condition for mechanical energy to be conserved is that there should be no frictional forces. This condition is only applicable in vacuum.

Name two examples in which the mechanical energy of a system remains constant.

Answer

1. Simple pendulum and

2. Motion of a freely falling body.

A pendulum with a bob of mass m is oscillating on either side from its resting position A between the extremes B and C at a vertical height h above A. What is the kinetic energy K and potential energy U when the pendulum is at positions

(i) A, (ii) B and (iii) C?

Answer

(i) For position A,

Pendulum has the maximum kinetic energy and potential energy is zero at its resting position.

So, K = mgh and U = 0

(ii) For position B,

The kinetic energy starts decreasing and the potential energy starts increasing.

So, K = 0 and U = mgh

(iii) At position C,

Kinetic energy K = 0 and potential energy U = mgh.

Name the type of energy possessed by the bob of a simple pendulum when it is at

(a) the extreme position,

(b) the mean position, and

(c) between the mean and extreme positions.

Answer

(a) When the bob is at extreme position the energy possessed is potential energy.

(b) When the bob is at mean position the energy possessed is kinetic energy.

(c) When the bob is in between mean position and extreme position the energy possessed by the bob are both kinetic energy and potential energy.

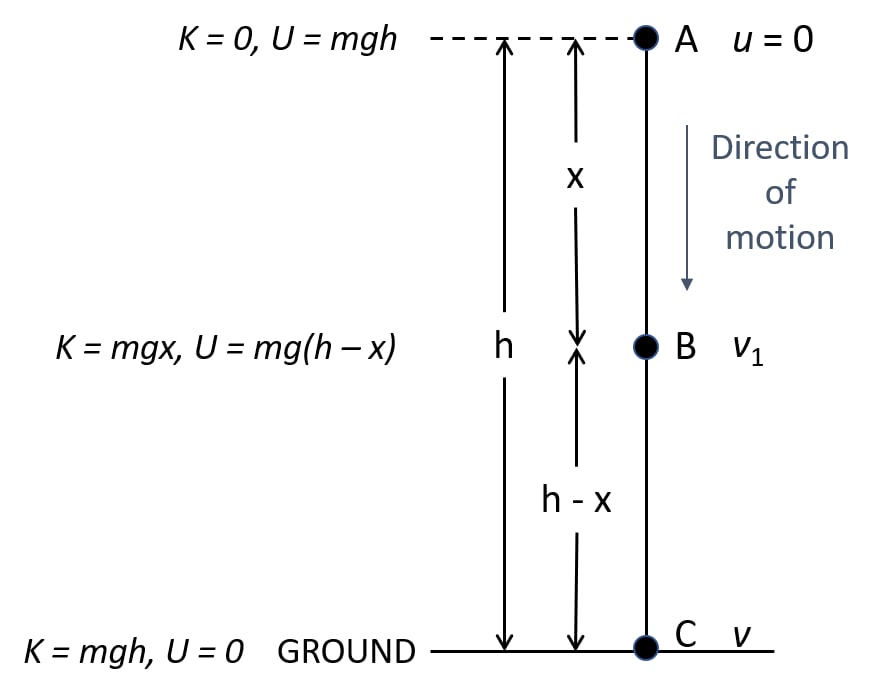
Show that the sum of kinetic energy and potential energy (i.e., total mechanical energy) is always conserved in the case of a freely falling body under gravity (with air resistance neglected) from a height h by finding it when

(i) the body is at the top,

(ii) the body has fallen a distance x,

(iii) the body has reached the ground.

Answer

We know that,

Kinetic energy + potential energy = constant

So, when a body falls from a height h under free fall

(i) At the position A — height h

Initial velocity = 0

Kinetic energy K = 0

Potential energy U = mgh

As, Total energy = KE + PE

Total energy = 0 + mgh

Total energy = mgh       (1)

(ii) At the position B — when it has fallen a distance x.

Then, velocity at B = v₁

Then u = 0, s = x, a = g

From equation of motion:
v² = u² + 2aS
v₁² = 0 + 2gx = 2gx

$\therefore \text{Kinetic energy K}= \dfrac{1}{2} \times m \times v_1^2 \\[0.5em] = \dfrac{1}{2} \times m \times 2gx \\[0.5em] = mgx$

∴ Potential energy U = mg (h – x)

Hence, total energy = K + U = mgx + mg (h – x) = mgh

Total energy = mgh       (2)

(iii) At position C (on the ground) —

Let the velocity acquired by the body on reaching the ground be v₂.

Then u = 0, s = h, a = g

We know,
v²= u² + 2aS
v₂² = 0 + 2gh
v₂² = 2gh

$\therefore \text{Kinetic energy K}= \dfrac{1}{2} \times m \times v_2^2 \\[0.5em] = \dfrac{1}{2} \times m \times 2gh \\[0.5em] = mgh$

And potential energy U = 0 (at the ground when h = 0)

So, total energy = K + U = mgh + 0

Total energy = mgh       (3)

Thus, from equation (1), (2) and (3) we note that the total mechanical energy i.e. the sum of kinetic energy and potential energy always remain constant at each point of motion and it is equal to the initial potential energy at height h.

A pendulum is oscillating on either side of its rest position. Explain the energy changes that take place in the oscillating pendulum. How does the mechanical energy remain constant in it? Draw necessary diagram.

Answer

The kinetic energy decreases and the potential energy becomes maximum at B.

After a moment the the to and fro movement starts again.

So, from B to A, again the potential energy changes into kinetic energy and this process repeat again and again.

So, when the bob in its state of to and from movement it has potential energy at the extreme position B or C and kinetic energy at resting position A.

It has both the kinetic energy and potential energy at an intermediate position.

However, the sum of kinetic and potential energy remain same at every point of movement.

A ball of mass 0.20 kg is thrown vertically upwards with an initial velocity of 20ms^-1. Calculate the maximum potential energy it gains as it goes up.

Answer

Given,

Mass = 0.20 kg

Initial velocity = 20ms^-1

We know,

$KE = \dfrac{1}{2} \times m \times v^2$

Maximum potential energy at the maximum height = initial kinetic energy

Substituting the values in the equation

$KE = \dfrac{1}{2} \times 0.20 \times 20^2 \\[0.5em] KE = \dfrac{1}{2} \times 0.20 \times 400$

∴ Maximum potential energy at the maximum height = Initial kinetic energy = 40 J

A stone of mass 500 g is thrown vertically upwards with a velocity of 15ms^-1.

Calculate:

(a) the potential energy at the greatest height,

(b) the kinetic energy on reaching the ground

(c) the total energy at its half waypoint.

Answer

Mass = 500g

Velocity = 15ms^-1

(a) We know,

Potential energy at maximum height = initial kinetic energy

mgh = $\dfrac{1}{2}$ mv²

Substituting the values in the equation we get,

$KE = \dfrac{1}{2} \times 0.500 \times 15^2 \\[0.5em] KE = \dfrac{1}{2} \times 0.500\times 225 \\[0.5em] = 56.25J$

∴ Potential energy at maximum height = Initial kinetic energy = 56.25J

(b) As we know that,

Kinetic energy on reaching the ground = potential energy at the greatest height

= 56.25J

(c) Total energy at its halfway point = $\dfrac{1}{2}$ (K + U) = 56.25J

A metal ball of mass 2kg is allowed to fall freely from rest from a height of 5m above the ground.

1. Taking g = 10ms^-1, calculate:
   1. the potential energy possessed by the ball when it is initially at rest.
   2. the kinetic energy of the ball just before it hits the ground?
2. What happens to the mechanical energy after the ball hits the ground and comes to rest?

Answer

Given,

Mass = 2 kg

Height = 5m

(a)

(i) the potential energy possessed by the ball when it is initially at rest = mgh = 2 x 10 x 5 = 100J

(ii) As we know that,

The kinetic energy of the ball just before hitting the ground = initial potential energy = mgh = 2 x 10 x 5 = 100J

(b) Mechanical energy of the ball gets converted into heat and sound energy after the ball hits the ground and comes to rest.

The diagram given below shows a ski jump. A skier weighing 60kgf stands at A at the top of ski jump. He moves from A and takes off for his jump at B.

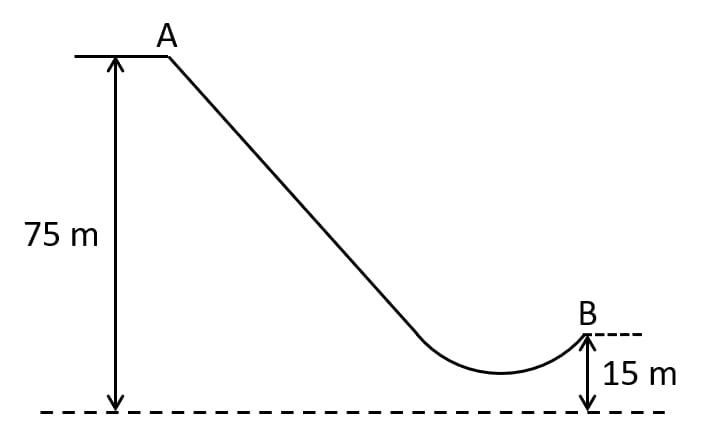
(a) Calculate the change in the gravitational potential energy of the skier between A and B.

(b) If 75% of the energy in part (a) becomes the kinetic energy at B, calculate the speed at which the skier arrives at B.

(Take g = 10 ms^-2).

Answer

Given,

Mass = 60 kg

(a)

$\text {Loss in potential energy} = \text{mg (h1 – h2)} \\[0.5em] = 60 \times 10\times (75-15) \\[0.5em] = 60 \times10 \times 60 \\[0.5em] = 3.6 \times 10^4 J \\[0.5em]$

(b) When kinetic energy at B is 75% of (3.6 × 10⁴)

$\text{Kinetic energy at B} = \dfrac{75}{100} \times 3.6 \times 10^4 \\[0.5em] = 27000J \\[0.5em] = 2.7 \times 10^4 J \\[0.5em]$

Since,

Kinetic energy = $\dfrac{1}{2}$ mv²

Substituting the values in equation we get,

$27000 = \dfrac{1}{2} \times 60 \times v^2 \\[0.5em] \Rightarrow 27000 = 1 \times 30 \times v^2 \\[0.5em] \Rightarrow v^2 = \dfrac{27000}{30} \\[0.5em] \Rightarrow v^2 = 900 \\[0.5em] \Rightarrow v = \sqrt{900} \\[0.5em] \Rightarrow v = 30 \\[0.5em]$

∴ The speed at which the skier arrives at B = 30ms^-1

A hydroelectric power station takes its water from a lake whose water level is 50m above the turbine. Assuming an overall efficiency of 40%, calculate the mass of water which must flow through the turbine each second to produce power output of 1MW. (Take g = 10 m s^-2).

Answer

Given,

Efficiency = 40%

Work done = 40% of potential energy

$\text{Work done} = 0.4 \times mgh \\[0.5em] = 0.4 \times m \times 10 \times 50 \\[0.5em] = 0.4 \times m \times 500 \\[0.5em] = 200 \times m$

$\text{Power} = \dfrac{\text{work done}}{\text{time}} \\[0.5em] 1MW = 200 \times \text {mass of water flowing per second} \\[0.5em] \Rightarrow 1 \times 10^6 = 200 \times m \\[0.5em] \Rightarrow \text m = \dfrac{1 \times 10^6 }{200} \\[0.5em] = 5000$

Hence,

Mass of water which must flow through the turbine = 5000Kg

The bob of a simple pendulum is imparted a velocity of 5 m s^-1 when it is at its mean position. To what maximum vertical height will it rise on reaching at its extreme position if 60% of its energy is lost in overcoming the friction of air?

(Take g = 10 m s^-2).

Answer

Given,

Energy lost = 0.6 x KE

KE = $\dfrac{1}{2}$ x mass x velocity²

Substituting the values we get,

$KE = \dfrac{1}{2} \times mass \times 5^2 \\[0.5em]$

Amount of energy lost,

$\text{Energy lost} = \dfrac{1}{2} \times mass \times 5^2 \times 0.6 \\[0.5em]$

Amount of energy available,

$\text{Energy available} = \dfrac{1}{2} \times mass \times 5^2 \times 0.4\\[0.5em]$

Applying the rule for the conservation of energy we get,

Kinetic energy available = potential energy

$\dfrac{1}{2} \times mass \times 5^2 \times 0.4 = mass \times gravity \times height\\[0.5em] \Rightarrow \dfrac{1}{2} \times 5 \times 5 \times 0.4 = 10 \times height\\[0.5em] \Rightarrow \dfrac{1}{2} \times 5 \times 2 = 10 \times height\\[0.5em] \Rightarrow 5 = 10 \times height\\[0.5em] \Rightarrow height = 0.5m \\[0.5em]$

∴ Maximum vertical height reached = 0.5m

The figure alongside shows a simple pendulum of mass 200 g. It is displaced from the mean position A to the extreme position B. The potential energy at position A is zero. At position B the bob is raised by 5 m.

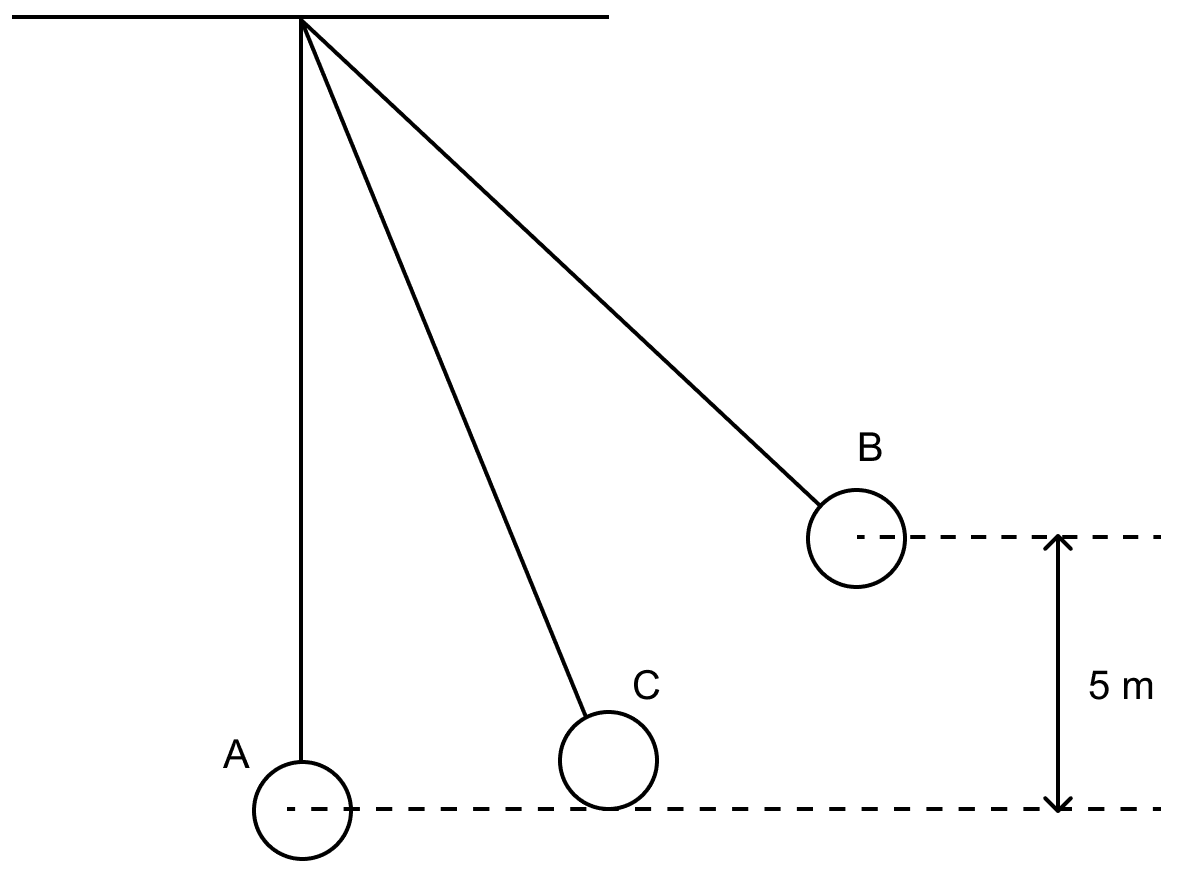
(a) What is the potential energy of the pendulum at position B ?

(b) What is the total mechanical energy at point C?

(c) What is the speed of the bob at position A when released from position B ? (Take g = 10 ms^-2)

Answer

Given,

h = 5 m, m = 200 g = 0.2 kg, g = 10 ms^-2

(i) Potential energy U_B at B is given by

U_B = m x g x h

Substituting the values we get,

$U_B = 0.2 \times 10 \times 5 \\[0.5em] \Rightarrow U_B = 10 J$

Hence, the potential energy of the pendulum at the position B = 10 J

(ii) Total mechanical energy at point C = 10 J

The total mechanical energy is same at all points of the path due to conservation of mechanical energy.

(iii) At A, bob has only kinetic energy which is equal to potential energy at B,

Therefore,

$\dfrac{1}{2} \times m \times (v_A)^{2} = U_B \\[0.5em] 0.5 \times 0.2 \times (v_A)^{2} = 10 \\[0.5em] (v_A)^{2} = \dfrac{10}{0.1} \\[0.5em] \Rightarrow v_A = \sqrt{100} \\[0.5em] \Rightarrow v_A = 10 \text{ m s}^{-1}$

(https://www.knowledgeboat.com/question/the-figure-alongside-shows-a-simple-pendulum-of-mass-200-g--297142821813660600)