The motion of a stationary rigid body in a straight path when a force is applied in the direction of force is called :
- rotational motion
- linear motion
- angular motion
- zigzag motion
Answer
linear motion
Reason — Linear motion refers to the motion of an object in a straight line, such as when a stationary rigid body moves in response to a force applied in the direction of the force.
The motion of a door when a force is applied on its handle is:
- rotational motion
- linear motion
- angular motion
- zig-zag motion
Answer
rotational motion
Reason — If a body is pivoted at a point and the force is applied on the body at a suitable point, it rotates the body about the axis passing through the pivoted point. This is the turning effect of force and the motion of body is called the rotational motion.
The moment of a force about a given axis depends on:
- only on the magnitude of force
- only on the perpendicular distance of force from the axis
- neither the force nor the perpendicular distance of force from the axis
- both, the force and its perpendicular distance from the axis.
Answer
both, the force and its perpendicular distance from the axis
Reason — The moment of a force (also known as torque) about an axis is calculated by multiplying the magnitude of the force by the perpendicular distance from the axis to the line of action of the force. So, it depends on both the magnitude of the force and its perpendicular distance from the axis.
For producing the maximum turning effect on a body by a given force, the perpendicular distance of the line of force from the axis of rotation should be :
- minimum
- it does not matter
- maximum
- zero
Answer
maximum
Reason — The torque produced by a force about an axis depends not only on the magnitude of the force but also on the perpendicular distance from the axis of rotation to the line of action of the force. Increasing this distance (having it at a maximum) maximizes the torque produced by the force.
The moment of force for anticlockwise moment is taken as ............... and for clockwise moment is taken as ...............
- positive, negative
- negative, positive
- positive, positive
- negative, negative
Answer
positive, negative
Reason — The moment of force for anticlockwise moment is taken as positive and for clockwise moment is taken as negative.
The direction of rotation of a pivoted body can be changed by changing:
- the direction of force
- the point of application of force
- both the direction of force and the point of application of force
- the magnitude of force
Answer
both the direction of force and the point of application of force
Reason — The direction of rotation of a pivoted body depends on both the direction of the applied force and the point at which the force is applied relative to the pivot point. Changing either or both of these factors can alter the direction of rotation of the body.
A couple is formed when ............... are not acting along the same line
- two unequal and parallel forces
- two equal and parallel forces
- two equal and opposite parallel forces
- two unequal and opposite parallel forces
Answer
two equal and opposite parallel forces
Reason — Two equal and opposite parallel forces, not acting along the same line form a couple.
As per the principle of moments in equilibrium :
- Sum of anticlockwise moments is greater than sum of clockwise moments
- Sum of anticlockwise moments is equal to sum of clockwise moments
- Sum of anticlockwise moments is less than sum of clockwise moments
- none of the above
Answer
Sum of anticlockwise moments is equal to sum of clockwise moments
Reason — According to the principle of moments in equilibrium :
sum of anticlockwise moments = sum of clockwise moments.
A body is acted upon by two unequal forces in opposite directions, but not in the same line. The effect is that:
- the body will only have rotational motion
- the body will only have translational motion
- the body will have neither rotational motion nor translational motion
- the body will have rotational as well as translational motion.
Answer
the body will have rotational as well as translational motion
Reason — When a body is acted upon by two unequal forces in opposite directions, but not in the same line, then the effect is that the body will have rotational as well as translational motion.
Out of the following which one is an example of dynamic equilibrium ?
(1) Moon revolving around the earth
(2) A pebble fixed at the end of a string whirling in a circular path
(3) An aeroplane moving at a constant height
(4) A beam balance balanced in a horizontal position.
- (3) and (4)
- (1), (2) and (3)
- (1) and (2)
- (1) and (3)
Answer
(1), (2) and (3)
Reason — Dynamic equilibrium refers to a state where two or more opposing processes occur at the same rate, resulting in a stable overall condition.
Moon revolving around the earth is an example of dynamic equilibrium as the gravitational force pulling the moon towards the Earth is balanced by the centrifugal force of the moon's motion, resulting in a stable orbit.
A pebble fixed at the end of a string whirling in a circular path is also an example of dynamic equilibrium as the tension in the string pulling the pebble towards the center is balanced by the centrifugal force of the pebble's motion, keeping it in a stable circular path.
An aeroplane moving at a constant height is also an example of dynamic equilibrium. It achieves dynamic equilibrium when upward lift on it balances its weight downwards.
A beam balance balanced in a horizontal position is not an example of dynamic equilibrium because the balance may remain still, it's a static equilibrium where opposing forces (gravity pulling down on each side of the balance) are already balanced without any ongoing processes happening.
State the condition when on applying a force, a body has:
(a) translational motion
(b) rotational motion.
Answer
(a) Translation motion is produced when a body is free to move.
(b) Rotational motion is produced when the body is fixed at a point.
State whether the moment of force is a scalar or vector quantity?
Answer
The moment of force is a vector quantity.
Write the expression for the moment of force about a given axis.
Answer
The expression for the moment of force is given by:
Moment of force about a given axis = Force × perpendicular distance of force from the axis of rotation.
State one way to reduce the moment of a given force about a given axis of rotation.
Answer
The moment of force can be reduced by decreasing the perpendicular distance of force from the axis of rotation.
State one way to obtain a greater moment of a force about a given axis of rotation.
Answer
We can obtain a greater moment of force by increasing the perpendicular distance of force from the axis of rotation.
Complete the following sentences:
(i) The S.I. unit of moment of force is ...............
(ii) In equilibrium algebraic sum of moments of all forces about the point of rotation is ................
(iii) In beam balance when the beam is balanced in a horizontal position, it is in ............... equilibrium.
(iv) The moon revolving around the earth is in ...............equilibrium.
Answer
(i) The S.I. unit of moment of force is Newton metre (Nm)
(ii) In equilibrium algebraic sum of moments of all forces about the point of rotation is zero.
(iii) In beam balance when the beam is balanced in a horizontal position, it is in static equilibrium.
(iv) The moon revolving around the earth is in dynamic equilibrium.
Define moment of force and state its S.I. unit.
Answer
The moment of force is equal to the product of the magnitude of the force applied and the perpendicular distance of the line of action of the force from the axis of rotation(or pivoted point).
The S.I unit of moment of force is Newton × meter = Newton meter (Nm)
State two factors affecting the turning effect of a force.
Answer
The following are the two factors on which moment of force about a point depends
(a) The magnitude of the force applied and,
(b) The distance of the line of action of the force from the axis of rotation(or the pivoted point).
When does a body rotate? State one way to change the direction of rotation of a body. Give a suitable example to explain your answer.
Answer
If a body is pivoted at a point and the force is applied on the body at a suitable point, it rotates the body about the axis passing through the pivoted point.
The direction of rotation can be changed by changing the direction of force.
Figures given below shows the clockwise and anticlockwise movement in a circle pivoted at the centre by changing the point of application of force F from A to point B


What do you understand by the clockwise and anticlockwise moment of force? When is it taken positive?
Answer
If the effect on the body is to turn it clockwise, moment of force is called the clockwise moment and it is taken as negative, while if the effect on the body is to turn it anticlockwise, moment of force is called the anticlockwise moment and it is taken as positive.
Why is it easier to open a door by applying the force at the free end of it?
Answer
It is easier to open the door by applying the force at the free end because when the perpendicular distance is large less force is required to turn the body.
The stone of hand flour grinder is provided with a handle near its rim. Give a reason.
Answer
The stone of hand flour grinder is provided with a handle near its rim so that by applying small force at the handle it can be rotated easily about the fixed point at its centre.
It is easier to turn the steering wheel of a large diameter than that of a small diameter. Give reason.
Answer
It is easier to turn the steering wheel of a large diameter in comparison to the wheel of a smaller diameter as less force is required in the first case due to the larger distance from the centre of the rim.
A spanner (or wrench) has a long handle. Why?
Answer
A spanner is provided with a long handle so as to create a larger turning moment with less force.
A jack screw is provided with a long arm. Explain why?
Answer
A jack screw which is used to lift a heavy vehicle has a long arm so that less force is needed to rotate it to raise or lower the vehicle.
The adjacent diagram shows a heavy roller, with its axle at O, which is to be raised on a pavement XY. If there is friction between the roller and pavement, show by an arrow on the diagram the point of application and the direction of force to be applied. If pivoted at 0, now will it go up?

Answer
Application of Force has to be done as shown in the diagram.
No, if pivoted at O it will not go up.

Define the moment of a couple. Write its S.I unit.
Answer
Moment of couple is product of either force and the perpendicular distance between the two forces.
The S.I unit of moment of couple is Nm
What do you mean by equilibrium of a body?
Answer
When a number of forces acting on a body produce no change in its state of rest or of linear or rotational motion, the body is said to be in equilibrium.
State the condition when a body is in
(i) static equilibrium.
(ii) dynamic equilibrium.
Give one example each of static and dynamic equilibrium.
Answer
(i) When a body remains in the state of rest under the influence of several forces, the body is said to be in static equilibrium.
Example — A toy lying on a floor is in static equilibrium.
(ii) When a body remains in the same state of motion (translation or rotational), under the influence of several forces, the body is said to be in dynamic equilibrium.
Example — An apple falling from a tree with a constant velocity.
State two conditions for a body, acted upon by several forces to be in equilibrium.
Answer
The two conditions for a body to be in equilibrium are
The resultant of all the forces acting on a body should be zero.
The algebraic sum of moments of all the forces acting on the body about the point of rotation should be zero.
State the principle of moments. Name one device based on it.
Answer
According to the principle of moments, if the algebraic sum of moments of all the forces, acting on the body, about the axis of rotation is zero, the body is in equilibrium. Therefore, as per the principle of moments,
sum of anticlockwise moments = sum of clockwise moments
For example, a physical balance works on the principle of moments.
A, B and C are the three forces each of magnitude 4N acting in the plane of paper as shown in figure. The point O lies in the same plane.

(i) Which force has the least moment about O? Give reason.
(ii) Which force has the greatest moment about O? Give reason.
(iii) Name the forces producing (a) clockwise, (b) anticlockwise moments.
(iv) What is the resultant torque about the point O?
Answer
(i)
We know that,
Moment of force = Force × Perpendicular distance
We can see from the given figure that vector C has least perpendicular distance from point O.
Hence, vector C will have least moment about O.
(ii) We know that,
Moment of force = Force × Perpendicular distance
We can see from the given figure that vector A has greatest perpendicular distance from point O
Hence, vector A will have greatest moment about O.
(iii)(a) Clockwise moments are produced by vectors A and B.
Reason : If turning effect on the body is clockwise then moment of force is called clockwise moment and it is taken as a negative value.
(b) Anticlockwise moment is produced by vector C.
Reason : If turning effect on the body is anticlockwise then moment of force is called anticlockwise moment and it is taken as a positive value.
(iv) Sum of torques due to vectors A, B and C = Resultant torque about point O
So, the resultant torque is 4.4Nm (clockwise direction).
A body is acted upon by two forces each of magnitude F, but in opposite directions. State the effect of the forces if
(a) both forces act at the same point of the body.
(b) the two forces act at two different points of the body at a separation r.
Answer
(a) As two forces of same magnitude are acting on a body at the same point and they are in opposite direction so the resultant force will be zero.
F – F = 0
(b) When two forces of same magnitude act on a body at two different points at a separation r and in opposite direction then the moment of force will be Fr
Moment of forces = F × r
Draw a neat labelled diagram to show the direction of two forces acting on a body to produce rotation in it. Also mark the point O about which the rotation takes place.
Answer

Two forces of magnitude F act at point A and point B. The body rotates in anticlockwise direction.
What do you understand by the term couple? State its effect on a body. Give two examples in our daily life where couple is applied to turn a body.
Answer
Two equal and opposite parallel forces, not acting along the same line form a couple.
A couple is always needed to produced a rotation.
Two examples in our daily life where we use couple are:
- Turning a water tap.
- Tightening the cap of a bottle.
Prove that
Moment of couple = Force x Couple arm.
Answer

At point A and point B two forces act which rotate the bar in anticlockwise direction.
The perpendicular distance between the two forces called AB is the couple arm.
Moment of force F at A = F x OA (anticlockwise)
Moment of force F at B = F x OB (anticlockwise)
Total moment of couple = F x OA + F x OB
F x (OA + OB) = F x AB
= F x d
Hence proved : Moment of force = Force x Couple arm
Describe a simple experiment to verify the principle of moments, if you are supplied with a metre rule, a fulcrum and two springs with slotted weights.
Answer

When we hang a metre rule horizontally from a fixed support with the help of a strong thread at point O as shown.
We use two slotted weights W1 and W2
We hang two spring balances on either side of the thread. The metre rule may tilt to one side.
We adjust the two spring balance distances from the support by keeping one at A and the other at B so that the scale again becomes horizontal.
Let W1 at a distance OA = l1 be the weight suspended on the right side of thread from the spring balance at A, while W2 at a distance OB = l2 be the weight suspended on the left side of thread from the spring balance at B.
The weight W1 tends to turn the scale clockwise and the weight W2 tends to turn the scale anticlockwise.
Clockwise moment = W1 × l1
Anticlockwise moment = W2 × l2
In equilibrium, when the scale is horizontal, it is found that
Clockwise moment = Anticlockwise moment
So, W1l1 = W2l2
Hence, the principle of moments is proved.
The moment of a force of 20 N about a fixed point O is 10 N m. Calculate the distance of the point O from the line of action of the force.
Answer
As we know,
Moment of Force = Force × Perpendicular distance from the point O
Moment of force = F × r
Substituting values in the above formula we get,
10 = 20 x r
⇒ r = = 0.5 m
Hence, distance of the point O from the line of action of the force is 0.5 m.
A nut is opened by a wrench of length 25 cm. If the least force required is 10 N, find the moment of force needed to turn the nut.
Answer
It is given that,
Required least force = 10N
r = 25cm = 0.25m
We know, Moment of force = F x r
Substituting the values of F and r we get,
Moment of force = 10 x 0.25 = 2.5 Nm
Hence, moment of force needed to turn the nut = 2.5 Nm
A 50 kg mass is being lifted by using a 1 metre long lever. If the length of the lever is reduced by 20%, how much more or less force is to be applied to achieve the same torque?
Answer
In first case,
mass = 50 kg
Initial length = R = 1m
F1 = mg = 50 x 9.8 = 490 N
Torque 1 = R x F1 = 1 x 490 = 490 Nm
Now in second case,
New length = r = R - 20% x R = R - 0.2 R = 0.8 R = 0.8 x 1 = 0.8m
Let required force = F2
So,
Torque 2 = r x F2 = 0.8 x F2
According to the question,
Torque 1 = Torque 2
490 = 0.8 x F2
F2 = = 612.5N
Here, F2-F1 = 612.5 - 490 = 122.5 N
∴ Force required to produce the same torque will increase by 122.5 N
A mechanic applies a force of 100 N at the end of a spanner to tighten a bolt. The length of the spanner is 0.5 metres. How much torque is exerted on the bolt? If the mechanic increases the force applied by 20% but holds the spanner closer at 0.4 metres, would it result in an increase or decrease of torque?
Answer
In first case,
F1 = 100 N
r1 = 0.5 m
Torque 1 = r1 x F1 = 0.5 x 100 = 50 Nm
∴ Torque exerted on the bolt = 50 Nm
In second case,
F2 = F1 + 20% x F1 = F1 + 0.2 x F1 = 1.2 F1 = 1.2 x 100 = 120 N
r2 = 0.4 m
Torque 2 = r2 x F2 = 0.4 x 120 = 48 Nm
Here, Torque 1 > Torque 2
Torque 1 - Torque 2 = 50 Nm - 48 Nm = 2 Nm
∴ The torque will decrease by 2 Nm
A wheel of diameter 2 m is shown in figure with axle at O. A force F = 2 N is applied at B in the direction shown in figure.

Calculate the moment of force about
(i) the centre O, and
(ii) the point A.
Answer
We know from the question,
F = 2 N
Diameter = 2m
So, Radius or OB = 1m
(i) Moment of force at O = F x r
Substituting the values of F and r we get,
(ii) Moment of force at A = F x r
Substituting the values of F and r we get,
The diagram shows two forces F1 = 5N and F2 = 3N acting at points A and B of a rod pivoted at a point O, such that OA = 2m and OB = 4m

Calculate:
(i) the moment of force F1 about O.
(ii) the moment of force F2 about O.
(iii) total moment of the two forces about O.
Answer
Given,
OA = 2m
OB = 4m
F1 = 5N
F2 = 3N
As we know,
Moment of force = F x r
Substituting the values of F and r
(i) Moment of force F1 about O
Therefore, moment of force F1 about O is 10Nm (anticlockwise)
(ii) Moment of force F2 about O
Therefore, moment of force F2 about O is 12Nm (clockwise)
(iii) Total moment of two forces about midpoint is
Therefore, total moment of two forces about O is 2Nm (clockwise)
Two forces each of magnitude 10N act vertically upwards and downwards respectively at the two ends A and B of a uniform rod of length 4m which is pivoted at its mid-point O as shown. Determine the magnitude of resultant moment of forces about the pivot O.

Answer
Given,
Ab = 4m
OA = 2m
OB = 2m
Force at A = 10N
Force at B = 10N
As we know ,
Moment of force = F x r
Substituting the values of F and r
Moment of force about o at point A
Moment of force about o at point B
Total moment of forces about the centre O
Total moment of force about the pivot O is 40 Nm (clockwise)
Figure shows two forces each of magnitude 10N acting at the points A and B at a separation of 50 cm, in opposite directions. Calculate the resultant moment of the two forces about the point (i) A, (ii) B and (iii) O, situated exactly at the middle of the two forces.

Answer
Given,
Force at A = 10N
Force at B = 10N
Distance between A and B = 50cm = 0.5m
(i) Resultant moment of two forces at point A is
Therefore, resultant moment of two forces at point A is 5 Nm (clockwise)
(ii) Resultant moment of two forces at point B is
Therefore, resultant moment of two forces at point B is 5 Nm (clockwise)
(iii) Perpendicular distance of point O from either of the forces F = 10N is 0.25 m
Moment of force F at point A about O
Moment of force F at point B about O
Resultant moment of two forces about o is
Therefore, Resultant moment of two forces about o is 5Nm (clockwise)
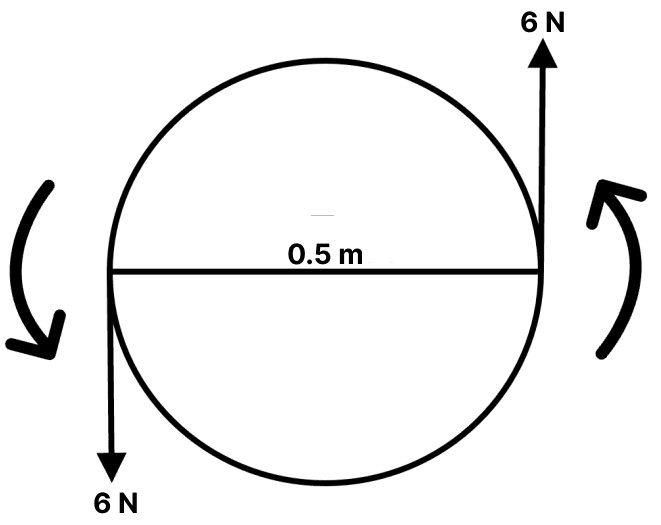
A steering wheel of diameter 0.5m is rotated anti-clockwise by applying two forces each of magnitude 6N. Draw a diagram to show the application of forces and calculate the moment of forces applied.
Answer
Moment of couple = either force × couple arm
= 6 x 0.5 = 3 Nm
A uniform metre rule is pivoted at its mid-point. A weight of 50 gf is suspended at one end of it. Where should a weight of 100gf be suspended to keep the rule horizontal?
Answer
Let us assume that a 50 gf weight produces an anticlockwise moment about the middle point ( 50 cm ).
Now, if a weight of 100 gf produces a clockwise moment about the middle point and d cm be the distance from the middle.
As we know, the principle of moments states that
Anticlockwise moment = Clockwise moment.
Therefore, a weight of 100gf will be suspended at a distance of 25cm to keep the ruler balanced.
A uniform metre rule balances horizontally on a knife edge placed at the 58 cm mark when a weight of 20gf is suspended from one end. (i) Draw a diagram of the arrangement. (ii) What is the weight of the rule?
Answer
(i) Diagram of the arrangement is shown below:

(ii) As we know, the principle of moments states that
Anticlockwise moment = Clockwise moment.
The diagram shows a uniform bar supported at the middle point O. A weight of 40 gf is placed at a distance 40cm to the left of the point O. How can you balance the bar with a weight of 80 gf?

Answer
From the given figure we can see that,
Anticlockwise moment = 40 gf × 40 cm
Clockwise moment = 80 gf × d cm
As we know, the principle of moments states that
Anticlockwise moment = Clockwise moment.
Therefore the bar will be in balanced position if weight of 80gf is placed at a point of 20cm to the right of O.
Figure shows a uniform metre rule placed on a fulcrum at its mid-point O and having a weight 40gf at the 10 cm mark and a weight of 20 gf at the 90 cm mark.
(i) Is the metre rule in equilibrium? If not, how will the rule turn?
(ii) How can the rule be brought in equilibrium by using an additional weight of 40gf?

Answer
(i) We know that when anticlockwise moment is equal to clockwise moment then the rule will be in equilibrium.
Let us check,
(a) Anticlockwise moment = Fr
(b) Clockwise moment = Fr
So, the meter rule will not be in equilibrium. It will turn in anticlockwise direction.
(ii) To balance the rule in equilibrium 40gf should be kept on right side.
Let distance from middle = d cm
So clockwise moment becomes
As we know, the principle of moments states that
Anticlockwise moment = Clockwise moment
Therefore,
∴ Distance from 0 cm mark = 50 cm + 20 cm = 70 cm
So, the additional weight should be placed at 70cm mark to bring the rule in equilibrium.
When a boy weighing 20 kgf sits at one end of a 4m long see-saw, it gets depressed at its end. How can it be brought to the horizontal position by a man weighing 40 kgf.
Answer
As we know, the principle of moments states that
Anticlockwise moment = Clockwise moment
So it is proved that horizontal position can be achieved if a person sits at a distance of 1m from the centre on the side opposite to the boy.
A physical balance has its arms of length 60 cm and 40 cm. What weight kept on a pan of longer arm will balance an object of weight 100 gf kept on other pan?
Answer
As we know, the principle of moments states that
Anticlockwise moment = Clockwise moment
Weight on the longer pan
So, a weight of 66.67gf kept on the pan of longer arm will balance the object of weight 100 gf kept on the other pan.
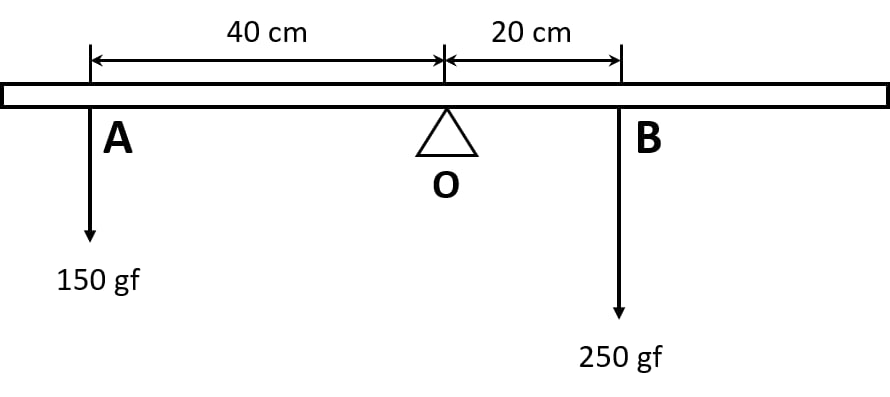
The diagram shows a uniform meter rule weighing 100 gf, pivoted at its centre O. Two weights 150gf and 250gf hang from the point A and B respectively of the metre rule such that OA = 40 cm and OB = 20 cm.
Calculate:
(i) the total anticlockwise moment about O,
(ii) the total clockwise moment about O,
(iii) the difference of anticlockwise and clockwise moment, and
(iv) the distance from O where a 100gf weight should be placed to balance the metre rule.
Answer
(i) The total anticlockwise moment about the centre o
(ii) The total clockwise moment about the centre o
(iii) The difference of anticlockwise and clockwise moment
(iv) As we know, the principle of moments states that
Anticlockwise moment = Clockwise moment
So d = 10 cm on the right side of o
A uniform metre rule of weight 10 gf is pivoted at its 0 mark.
(i) What moment of force depresses the rule?
(ii) How can it be made horizontal by applying a least force?
Answer
(i) Moment of force = Fr
Substituting the values of F and r we get,
(ii) In order to make the rule horizontal by applying least force distance has to be max as moment of force will remain same.
So,
Therefore, a force of 5 gf upwards at 100 cm can balance the rule.
A uniform half metre rule can be balanced at the 29.0 cm mark when a mass 20g is hung from its one end.
(a) Draw a diagram of the arrangement.
(b) Find the mass of the half metre rule.
(c) In which direction would the balancing point shift if 20g mass is shifted inside from its one end?
Answer
(a) Diagram of the arrangement is shown below:

(b) Suppose, if the mass of the meter rule be M.
Given, uniform meter rule, so weight (Mg) will act at 25 cm.
Mg produces anticlockwise moment about point o.
Now, in order to balance the 20g weight is tied at 50cm point and it acts in the clockwise direction.
As we know, the principle of moments states that
Anticlockwise moment = Clockwise moment
The weight of half the meter rule is 105 g.
(c) The balancing point will shift towards the 25 cm mark.
A uniform metre rule of mass 100 g is balanced on a fulcrum at mark 40 cm by suspending an unknown mass m at the mark 20 cm.
(i) Find the value of m.
(ii) To which side the rule will tilt if the mass m is moved to the mark 10 cm?
(iii) What is the resultant moment now?
(iv) How can it be balanced by another mass 50 g?
Answer
(i) As we know, the principle of moments states that
Anticlockwise moment = Clockwise moment
(ii) When the mass m is shifted to mark 10cm , it results in rule being shifted on the side of mass m in anticlockwise direction.
(iii) Anticlockwise moment is produced when a mass of m grams is moved towards the mark of 10cm.
Therefore, the resultant moment will be
(iv) As we know, the principle of moments states that
Anticlockwise moment = Clockwise moment
So,
Hence, we can balance 50gm at 50cm
In figure below, a uniform bar of length l m is supported at its ends and loaded by a weight W kgf at its middle. In equilibrium, find the reactions R1 and R2 at the ends.

[Hint : In equilibrium R1 + R2 = W and ]
Answer
As we know, the principle of moments states that
Anticlockwise moment = Clockwise moment
R1 + R2 = W
Given, the system is in equilibrium so
Since, R1 = R2 and 2R1 = W
Therefore, R1 = W/2 = R2
With respect to centre of gravity, which of the following statements are correct?
- The position of centre of gravity depends on its shape.
- It is not necessary that the centre of gravity of a body should always be within the material of the body.
- A body of weight W can be considered as a point particle of weight W at its centre of gravity.
- All of the above
Answer
All of the above
Reason — With respect to centre of gravity :
- The position of centre of gravity depends on its shape i.e., on the distribution of mass.
- It is not necessary that the centre of gravity of a body should always be within the material of the body.
- By the concept of centre of gravity, a body of weight W can be considered as a point particle of weight W at its centre of gravity.
The centre of gravity of a body is the point about which the algebraic sum of moments of weights of all the particles constituting the body is:
- 1
- > 1
- < 1
- 0
Answer
0
Reason — The centre of gravity of a body is the point about which the algebraic sum of moments of weights of all the particles constituting the body is zero. This is because the center of gravity is chosen in such a way that the torques (moments) due to the weight of the individual particles balance out, resulting in a net torque of zero.
The centre of gravity of a hollow cone of height h is at distance x from its vertex where the value of x is:
Answer
Reason — The centre of gravity of a hollow cone is at a height from the base.
Hence, from the vertex the height is :
h - = =
Where should the centre of gravity of a body be located for stable equilibrium?
- above the base
- near the geometric centre
- can be anywhere
- both (1) and (2)
Answer
both (1) and (2)
Reason — For stable equilibrium, the center of gravity of a body should be located above the base of the body. Additionally, it should be as close as possible to the geometric center.
Two objects have the same mass but different shapes. Which object would have a higher centre of gravity?
- the one with a larger base
- the one with a smaller base
- both would have the same centre of gravity
- it depends on the material of the object.
Answer
the one with a smaller base
Reason — An object with a larger base of support will have a low centre of gravity because the distribution of mass is spread out over a larger area, which tends to lower the center of gravity whereas that with a smaller base will have a higher centre of gravity because the mass is concentrated over a smaller area.
Can the centre of gravity of a body be situated outside its material of the body? Give an example.
Answer
Yes, the centre of gravity can be outside the material of the body.
In the case of a uniform ring the centre of gravity is in the centre of the ring and that point is outside the material of the ring.
What is the position of centre of gravity of a:
(a) rectangular lamina
(b) cylinder?
Answer
Centre of gravity for the following figures are as follows :
(a) Rectangular lamina — at the point of intersection of the diagonals.
(b) Cylinder — at the mid point of the axis of cylinder.
At which point is the centre of gravity situated in :
(a) A triangular lamina and
(b) A circular lamina?
Answer
The centre of gravity for the following figures are as follows :
(a) A triangular lamina — at the point of intersection of the medians.
(b) A circular lamina — at the centre of the circular lamina.
Where is the centre of gravity of a uniform ring situated?
Answer
The centre of gravity of a uniform ring is situated at the centre of the ring.
State whether the following statements are true or false.
(i) 'The position of centre of gravity of a body remains unchanged even when the body is deformed'.
(ii) 'The centre of gravity of a freely suspended body always lies vertically below the point of suspension'.
Answer
(i) False
Reason — The position of the center of gravity of a body depends on its mass distribution. When a body is deformed, its mass distribution can change, leading to a potential shift in the position of its center of gravity.
(ii) True
Define the term 'centre of gravity of a body'.
Answer
The centre of gravity of a body is defined as the point about which the algebraic sum of moments of weights of particles constituting the body is zero and the entire weight of the body is to act at this point.
State a factor on which the position of centre of gravity of a body depend? Explain your answer with an example.
Answer
The position of the centre of gravity of any body will depend on the type of shape it has i.e. (on the distribution of mass on the body) in it. It changes if the shape of the body is deformed.
For example, the centre of gravity of a wire is a its mid point. However, if the wire is turned in a way that it makes a circle then its centre of gravity will be at the centre of the circle.
A square card board is suspended by passing a pin through a narrow hole at its one corner. Draw a diagram to show its rest position. In the diagram mark the point of suspension by the letter S and centre of gravity by the letter G.
Answer
The diagram is shown below:

Humans bend forward when they carry a heavy load on their back. Give reason.
Answer
When a heavy load is placed on the back, the center of gravity of the body shifts backward. To prevent falling backward and to keep the body’s center of gravity above the feet (the base of support), a person bends forward. This forward bending compensates for the backward shift, allowing the person to remain stable and balanced while carrying the load.
You are assigned to look after a loading of a cargo ship with containers marked A and B. The A type containers are 50% more heavier than B type containers. What precaution would you take and why so that the ship sails smoothly even in rougher seas?
Answer
Precaution:
To ensure the ship sails smoothly, the heavier A-type containers should be loaded closer to the ship’s center of gravity (near the bottom and central part of the ship), while the lighter B-type containers should be loaded on top or towards the sides.
Reason:
A-type containers are 50% heavier than B-type containers. If these heavy containers are loaded improperly (e.g., on the upper decks or on one side), they will raise the ship’s center of gravity and make it unstable, increasing the risk of tilting, especially in rough seas.
A uniform flat circular rim is balanced on a sharp vertical nail by supporting it at a point A, as shown in figure. Mark the position of centre of gravity of the rim in the diagram by the letter G.

Answer
The position of centre of gravity of the rim is marked by the letter G in the below diagram:

Figure shows three pieces of card board of uniform thickness cut into three different shapes. On each diagram draw two lines to indicate the position of centre of gravity G.



Answer
The position of centre of gravity G for the three pieces of card board are marked in the below diagrams:



Explain how you will determine experimentally the position of centre of gravity for a triangular lamina (or a triangular piece of card board).
Answer

To determine centre of gravity for a triangular lamina, make three fine holes a, b, c near its edges. After that, suspend it from hole a along with a plumb line. Ensure that the lamina is freely suspended. When it comes to rest, draw straight line ad along the plumb line. Repeat the experiment by suspending the lamina through hole 'b' and then through hole 'c'. This gives us two straight lines, be and cf respectively. The three lines ad, be and cf intersect each other at a common point G. This common point G is the position of the centre of gravity of triangular lamina.
Which of the following quantities remains constant in uniform circular motion?
- Velocity
- Speed
- Acceleration
- Both velocity and speed
Answer
Speed
Reason — In uniform circular motion, where an object travels along a circular path at a constant speed, the direction of motion changes continuously, implying the presence of acceleration. Hence, velocity changes due to change in direction and speed remains constant.
The direction of motion in circular motion :
- is linear
- is along the tangent at that point of the circular path
- towards the centre
- none of these
Answer
is along the tangent at that point of the circular path
Reason — In circular motion, the direction of motion of an object is along the tangent at that point of the circular path where the object is located at any given moment.
The direction of centripetal force is always :
- along the tangent at that point of the circular path
- towards the centre
- outwards from the centre
- none of the above
Answer
towards the centre
Reason — The centripetal force is always directed towards the center of the circular path. It is responsible for keeping an object moving along the curved path by continuously changing its direction towards the center without altering its speed. This force acts perpendicular to the direction of motion, pointing inward, towards the center of the circular path.
Centrifugal force is :
- a real force
- the force of reaction of centripetal force
- a fictitious force
- directed towards the centre of the circular path
Answer
a fictitious force
Reason — The centrifugal force is a fictitious force because it is assumed to exist only to explain observations made from the frame of reference of an observer who is also moving in a circular motion along with the object that is being observed.
The difference between centrifugal force and centripetal force is :
- they both act in the same direction
- they both act in opposite direction
- they both have different magnitudes
- none of the above
Answer
they both act in opposite direction
Reason — Centripetal Force is a real force which acts towards the centre of the circle whereas centrifugal force is an assumed force which acts away from centre of the circle. Both the forces act in opposite directions.
Which of the following is an example of uniform circular motion?
- a car accelerating on a straight road
- a pendulum swinging back and forth
- a satellite orbiting the earth at a constant altitude
- a ball rolling down a hill
Answer
a satellite orbiting the earth at a constant altitude
Reason —
A satellite orbiting the Earth at a constant altitude experiences uniform circular motion because it maintains a constant speed while continuously moving along a circular path around the Earth.
The car moving along a straight path and may be changing its speed, but it is not following a circular path.
A pendulum exhibits periodic motion as it swings back and forth due to gravity but it is not circular motion.
The ball is rolling along a sloped path, not a circular one.
Assertion (A): When a beam is in static equilibrium, the sum of clockwise moments is equal to the sum of anticlockwise moments.
Reason (R): According to the principle of moments for a body in equilibrium, the sum of moments acting in one direction must be equal to the sum of moments in opposite direction.
- Both A and R are true and R is the correct explanation of A
- Both A and R are true and R is not the correct explanation of A
- assertion is false but reason is true
- assertion is true but reason is false
Answer
Both A and R are true and R is the correct explanation of A.
Explanation
Assertion (A) is true because when the sum of the clockwise moments acting on the beam is equal to the sum of the anticlockwise moments, their resultant sum is zero and the beam has no rotational motion. Hence, it is in static equilibrium.
Reason (R) is true because it provides a logical explanation for Assertion (A), stating the principle of moments for a body in equilibrium, which aligns with the definition of static equilibrium.
Assertion (A): A heavier object placed at a far distance from the pivot point will have the same moment as a lighter object placed close to the pivot point.
Reason (R): The moment of force is determined by the magnitude of the force along with its distance from the pivot point.
- Both A and R are true and R is the correct explanation of A
- Both A and R are true and R is not the correct explanation of A
- assertion is false but reason is true
- assertion is true but reason is false
Answer
assertion is false but reason is true.
Explanation
The moment of a force is equal to the product of the magnitude of the force and the perpendicular distance of the line of action of the force from the axis of rotation. Hence, a heavier object placed at a far distance from the pivot point will have a greater moment than a lighter object placed close to the pivot point. Therefore, Assertion (A) is false.
Reason (R) is true. The moment of force is determined by the magnitude of the force along with its distance from the pivot point.
Assertion (A): The centre of gravity of an irregularly-shaped object always lies at its geometric centre.
Reason (R): The centre of gravity depends on the distribution of mass within an object.
- Both A and R are true and R is the correct explanation of A
- Both A and R are true and R is not the correct explanation of A
- assertion is false but reason is true
- assertion is true but reason is false
Answer
assertion is false but reason is true.
Explanation
Assertion (A) is false. The center of gravity of an irregularly-shaped object does not always coincide with its geometric center. It depends on the distribution of mass within the object.
Reason (R) is true. The center of gravity does depend on the distribution of mass within an object.
Is it possible to have an accelerated motion with a constant speed? Name such type of motion.
Answer
Yes, an accelerated motion with constant speed is possible. Uniform circular motion is such type of motion.
Give an example of motion in which speed remains uniform, but the velocity changes.
Answer
Motion of artificial satellite is one of the cases where speed is same however velocity changes.
Name the force required for circular motion. State its direction.
Answer
Centripetal force is required for circular motion. The direction of Centripetal force is always directed towards the centre of circle.
Is centrifugal force a real force?
Answer
No the centrifugal force is a fictitious force.
State whether the following statements are true or false by writing T/F against them.
(a) Earth moves around the Sun with a uniform velocity.
(b) The motion of Moon around Earth in a circular path is an accelerated motion.
(c) A uniform linear motion is unaccelerated, while a uniform circular motion is an accelerated motion.
(d) In a uniform circular motion, the speed continuously changes because the direction of the motion changes.
(e) A boy experiences a centrifugal force on his hand when he rotates a piece of stone tied at one end of a string, holding the other end in the hand.
Answer
(a) False
Reason — The Earth does not move around the Sun with uniform velocity. It follows an elliptical orbit, which means its speed varies as it travels around the Sun.
(b) True
Reason — The motion of Moon around Earth in a circular path is an accelerated motion because in a circular motion, the direction of velocity is continuously changing, which in turn causes change in acceleration.
(c) True
Reason — In uniform linear motion, an object moves in a straight line with a constant speed. As there is no change in speed or direction, hence, there is no acceleration. On the other hand, in uniform circular motion, an object moves in a circular path at a constant speed and the direction of the object's velocity continuously changes as it moves around the circle. This change in direction results in centripetal acceleration.
(d) False
Reason — In uniform circular motion, the speed of the object remains constant, but its velocity, which includes both speed and direction, changes continuously.
(e) False
Reason — When the boy rotates the stone tied to a string and holds the other end in his hand, the force experienced by his hand is centripetal, not centrifugal.
Centripetal force is the force directed toward the center of the circular path, required to keep an object moving in a circular motion. Centrifugal force, on the other hand, is a fictitious force that appears to act outward from the center of rotation in a rotating reference frame.
Differentiate between uniform linear motion and a uniform circular motion.
Answer
| Uniform Linear Motion | Uniform Circular Motion |
|---|---|
| The body moves along a straight line | The body moves along a circular path. |
| Speed and direction both are constant | Speed is constant but direction changes continuously. |
| Not an accelerated motion | An accelerated motion. |
What is a centripetal force
Answer
The force acting on a body moving in a circular path, in a direction towards the centre of circular path is called Centripetal force.
Explain the motion of a planet around the Sun in an elliptical path.
Answer
The motion of a planet around the Sun in an elliptical path is an example of uniform circular motion. The gravitational force of attraction on the planet by the Sun provides the necessary centripetal force for this uniform circular motion as it is always directed towards the centre of the Sun.
(a) How does a centripetal force differ from a centrifugal force with reference to the direction in which they act?
(b) Is centrifugal force the force of reaction of the centripetal force?
(c) Compare the magnitudes of centripetal and centrifugal force.
Answer
(a) Both the forces act in opposite direction with reference to the direction.
(b) No, centrifugal force is not the force of reaction of the centripetal force.
(c) The magnitude of centripetal and centrifugal force is 1:1
State two differences between the centripetal and centrifugal force.
Answer
| Centripetal Force | Centrifugal Force |
|---|---|
| A real force. | An assumed force. |
| Acts towards the centre of the circle. | Acts away from centre of the circle. |
Explain the meaning of uniform circular motion. Why is such motion said to be accelerated?
Answer
When a body moves with a constant speed in a circular path, its motion is said to be in uniform circular motion.
Uniform circular motion is said to be accelerated as the velocity changes with continuous change in direction of motion.
Draw a neat labelled diagram for a particle moving in a circular path with a constant speed. In your diagram show the direction of velocity at any instant.
Answer
The below diagram shows a particle moving in a circular path with a constant speed and its direction of velocity:

A uniform circular motion is an accelerated motion. Explain it. State whether the acceleration is uniform or variable? Name the force responsible to cause this acceleration. What is the direction of force at any instant? Draw diagram in support of your answer.
Answer
A uniform circular motion is accelerated as the speed is same however the direction changes continuously. So, it is said to be a uniform accelerated motion.
Centripetal force is required for this acceleration and its direction is towards the centre of the circular path.

A small pebble tied at one end of a string is placed near the periphery of a circular disc, at the center of which the other end of the string is tied to a peg. The disc is rotating about an axis passing through its centre.
(a) What will be your observation when you are standing outside the disc? Explain.
(b) What will be your observation when you are standing at the centre of the disc. Explain.
Answer
(a) The pebble seems to move in a circular path when we are sitting outside the circular disc.
(b) The pebble seems to be stationary in front of us when we are standing at the centre of the disc.
A piece of stone tied at the end of a thread is whirled in a horizontal circle with uniform speed with the help of hand.
Answer the following questions:
(a) Is the velocity of stone uniform or variable?
(b) Is the acceleration of stone uniform or variable?
(c) What is the direction of acceleration of stone at any instant?
(d) Which force provides the centripetal force required for circular motion?
(e) Name the force and its direction which acts on the hand.
Answer
(a) Velocity of stone is variable.
(b) Acceleration of stone is variable.
(c) The direction of acceleration of stone at any instance is to the centre of circular path.
(d) The Tension in the string provides the centripetal force.
(e) The force acting on the hand is the reaction tension force, directed away from the center.