The angle which the ............... ray makes with the ............... at the point of incidence is called angle of incidence.
- reflected, mirror
- incidence, mirror
- incidence, normal
- reflected, normal
Answer
incidence, normal
Reason — The angle which the incidence ray makes with the normal at the point of incidence is called angle of incidence.
Regular reflection occurs when a beam of light falls on a ...............
- smooth surface
- polished surface
- rough surface
- Both (a) and (b)
Answer
Both (a) and (b)
Reason — Regular reflection occurs when a beam of light falls on a smooth and polished surface, such as a plane mirror. The reflected beam is also parallel and it is in a fixed direction. It can be seen only from a particular direction.
According to the law of reflection:
= Constant
= Constant
i + r = Constant
i = r
Answer
i = r
Reason — According to the law of reflection the angle of incidence is equal to the angle of reflection.
The image formed due to the actual intersection of the reflected rays is :
- virtual
- diminished
- real
- enlarged
Answer
real
Reason — The image which can be obtained on a screen is called a real image. It is inverted. It is formed when light rays after reflection actually intersect.
The image formed by a plane mirror is:
- erect and diminished
- erect and enlarged
- inverted and of same size
- erect and of same size
Answer
erect and of same size
Reason — The characteristics of an image formed by a plane mirror are — upright (or erect), virtual and of the same size as the object.
The image formed by a plane mirror is:
- real
- virtual
- virtual with lateral inversion
- real with lateral inversion
Answer
virtual with lateral inversion
Reason — The characteristics of an image formed by a plane mirror are — upright (or erect), virtual.
A concave mirror forms ............... image whereas a convex mirror forms ...............
- real, real
- virtual, real
- virtual, virtual
- real, virtual
Answer
real, virtual
Reason — For a distant object, the image formed by a concave mirror is real. The image of an object formed by a plane mirror or a convex mirror is virtual.
Which of the following combination of letters does not show lateral inversion ?
- A, C, I
- M, T, V
- D, L, A
- X, Y, Z
Answer
M, T, V
Reason — Lateral inversion is the interchange of left and right sides in a plane mirror image. The letters M, T, and V do not exhibit noticeable lateral inversion in their mirror image due to their inherent symmetry about a vertical line passing through their midpoint.
If the object is shifted by a distance d towards a plane mirror, the image will shift by distance ............... towards the mirror.
- d
- 2d
- 3d
- None of the above
Answer
d
Reason — If the object is shifted by a distance d towards a plane mirror, the image will also shift by a distance d towards the mirror.
Select the luminous object(s) from the following :
Sun, Moon, Earth, Shooting star, Fire
Answer
Sun, Shooting star, Fire as they emit light by themselves.
What do you mean by reflection of light ?
Answer
The return of light into the same medium after striking a surface is called reflection of light.
State which surface of the plane mirror reflects most of the light incident on it — the front smooth surface or the back silvered surface.
Answer
The back silvered surface of the plane mirror reflects most of the light incident on it.
A light ray is incident normally on a plane mirror.
(a) What is its angle of incidence?
(b) What is the direction of reflected ray? Show it on a diagram.
Answer
(a) When the ray of light is incident normally on a plane mirror the angle of incidence = 0°.
(b) The direction of reflected ray is same as the incident ray i.e., it retraces the path as shown below.

For a ray reflected on a plane mirror, find the ratio of sin i/sin r
Answer
The ratio of = 1
According to the laws of reflection angle of incidence = angle of reflection, hence sin i = sin r and we get the ratio as 1.
Light from a torch is reflected by a white sheet of paper and a black polished mica sheet. Which of the two will produce a stronger reflected beam ?
Answer
Black polished mica sheet will produce a stronger reflected beam as highly polished and silvered surfaces reflect almost the entire light falling on them.
A light ray strikes a mirror and retraces its path. What is the angle of incidence and angle of reflection ?
Answer
For a ray incident normally on a plane mirror, the angle of incidence is i = 0°, therefore the angle of reflection r = 0°. Thus, a ray of light incident normally on a mirror is reflected along the same path.
Explain the following terms —
(a) plane mirror
(b) incident ray
(c) reflected ray
(d) angle of incidence
(e) angle of reflection.
Draw diagram/diagrams to show them.
Answer
(a) Plane mirror — It is made from few mm thick glass plate. One surface of the glass plate is polished to a high degree of smoothness. This forms the front surface of the mirror and the other surface is silvered (i.e., silver mercury or some suitable material is deposited over it). The silvered surface is further coated with some opaque material so as to protect the silvering on it.
The two surfaces of the plane mirror are shown below —

(b) Incident ray — the ray of light striking a reflecting surface is called the incident ray.
(c) Reflected ray — the light ray obtained after reflection from the surface in the same medium in which the incident ray is travelling is called reflected ray.
(d) Angle of incidence — The angle which the incident ray makes with the normal at the point of incidence, is called angle of incidence.
It is denoted by the letter i.
(e) Angle of reflection — The angle which the reflected ray makes with the normal at the point of incidence, is called angle of reflection.
It is denoted by the letter r.
Below diagram illustrates the Incident ray, Reflected ray, Angle of incidence and Angle of reflection:

Differentiate between reflection of light from a plane mirror and that from a plane wall.
Answer
| Reflection of light from a plane mirror | Reflection of light from a plane wall |
|---|---|
| When a ray of light is incident on a smooth and polished surface such as a plane mirror then regular reflection occurs. | When a ray of light is incident on a plane wall then irregular reflection occurs. |
| When a parallel beam of light is incident on a plane mirror, the reflected beam is also parallel and it is in a fixed direction . | When rays fall at different points on a plane wall then due to uneven surface at different points, light rays gets reflected in different directions. As a result, The reflected light spreads over a wide area and it does not follow a particular direction. |
State the two laws of reflection of light.
Answer
The two laws of reflection are —

- The angle of incidence i is equal to the angle of reflection r (i.e., ∠i = ∠r)
∠AON = ∠BON - The incident ray, the reflected ray and the normal at the point of incidence, lie in the same plane.
AO, ON and OB are in one plane.
Draw a diagram to show the reflection of a ray of light by a plane mirror. In the diagram, label the incident ray, the reflected ray, the normal, the angle of incidence and the angle of reflection.
(a) Write three characteristics of image formed by a plane mirror?
(b) How is the position of the image related to the position of the object?
Answer
Below is the labelled diagram showing the reflection of a ray of light by a plane mirror:

(a) The characteristics of an image formed by a plane mirror are —
- Image is upright (or erect).
- Image is virtual.
- Image is of the same size as the object.
(b) The position of the image is situated at the same perpendicular distance behind the mirror as the object is in front of it.
Differentiate between a real and a virtual image.
Answer
The difference between a real and a virtual image are as follows —
| Real image | Virtual image |
|---|---|
| A real image is formed due to actual intersection of the reflected rays. | A virtual image is formed when the reflected rays appear to meet when produced backwards. |
| A real image can be obtained on a screen. | A virtual image cannot be obtained on a screen. |
| A real image is inverted with respect to the object | A virtual image image is erect with respect to the object. |
| Example — The image of a distant object formed by a concave mirror. | Example — The image of an object formed by a plane mirror or by a convex mirror. |
What is meant by lateral inversion of an image in a plane mirror? Explain it with the help of a ray diagram.
Answer
The interchange of the left and right sides in the image of an object in a plane mirror is called lateral inversion.
Below diagram illustrates lateral inversion of an image:

The letters on the front of an ambulance are written laterally inverted like ƎƆИA⅃UꓭMA. Give reason.
Answer
The letters on the front of an ambulance are written laterally inverted like ƎƆИA⅃UꓭMA so that the driver of the vehicle moving ahead of the ambulance reads the word laterally inverted as AMBULANCE, in his rear view mirror, and gives way to the ambulance first.
With the help of diagrams, explain the difference between regular and irregular reflection.
Answer
Regular reflection — It occurs when a beam of light falls on a smooth and polished surface, such as a plane mirror. In the figure shown below, a parallel beam of light is incident on a plane mirror. The reflected beam is also parallel and it is in a fixed direction. It can be seen only from a particular direction.

Irregular reflection — It occurs when a beam of light falls on a rough or ordinary surface such as the walls of a room or the page of a book which appear smooth but have many small projections over it.
In the figure given below, light rays fall at different points on a rough surface and each ray gets reflected from it obeying the laws of reflection of light. Due to uneven surface at different points, light rays gets reflected in different directions and give rise to diffused or irregular reflection.

As a result, reflected light spreads over a wide area and it does not follow a particular direction. Hence, reflected light can be seen from anywhere.
State the laws of reflection and describe an experiment to verify them.
Answer
The two laws of reflection are —

The angle of incidence i is equal to the angle of reflection r (i.e., ∠i = ∠r)
∠AON = ∠BONThe incident ray, the reflected ray and the normal at the point of incidence, lie in the same plane.
AO, ON and OB are in one plane.
Experimental verification —
Fix a sheet of white paper on a drawing board and draw a line MM1 as shown below. On this line, take a point O nearly at the middle of it and draw a line OA such that ∠MOA is less than 90° (say, ∠MOA = 60°). Then draw a normal ON on line MM1 at point O, and place a small plane mirror vertically by means of a stand with it's silvered surface on the line MM1.
Now fix two pins P and Q vertically at some distance (say 5 cm) apart on line OA, on the board. Keeping eye on the other side of the normal (but on the same side of mirror), see clearly the images P'and Q' of the pins P and Q.
Now fix a pin R such that it is in line with the images P' and Q' as observed in the mirror. Now fix one more pin S such that the pin S is also in line with the pin R as well as the images P' and Q' of pins P and Q.
Draw small circles on paper around the positions of pins as in figure. Remove the pins and draw a line OB joining the point O to the pin points S and R.
As we can observe, AO is the incident ray, OB is the reflected ray, ∠AON = i is the angle of incidence and ∠BON = r is the angle of reflection. The angles AON and BON are measured and recorded in the observation table.
The experiment is repeated for the ∠MOA equal to 50°, 40° and 30°.
Observation table —
| S. No. | Angle of incidence, i = ∠AON (in degrees) | Angle of reflection r = ∠BON (in degrees) |
|---|---|---|
| 1 | 30 | 30 |
| 2 | 40 | 40 |
| 3 | 50 | 50 |
| 4 | 60 | 60 |
From the above observation table, we find that in each case, angle of incidence is equal to the angle of reflection. This verifies the first law of reflection.
The experiment is being performed on a flat drawing board, with mirror normal to the plane on which white sheet of paper is being fixed. Since the lower tips of all the four pins lie on the same plane (i.e., the plane of paper), therefore, the incident ray, the reflected ray and the normal at the point of incidence, all lie in one plane. This verifies the second law of reflection.
The figure given below shows an incident ray AO and the normal ON on a plane mirror. The angle which the incident ray AO makes with the mirror is 30°.

(a) Find the angle of incidence.
(b) Draw the reflected ray and then find the angle between the incident and reflected rays.
Answer
(a) The angle of incidence = 90° - 30° = 60°
(b) Diagram showing the reflected ray is given below:

The angle between the incident ray and the reflected ray = angle of incidence + angle of reflection
As we know,
Angle of incidence = Angle of reflection = 60°
Therefore, we get,
60° + 60° = 120°
Hence, the angle between the incident ray and reflected ray = 120°
The diagram below shows a point object P in front of a plane mirror MM1.
(a) Complete the diagram by taking two rays from the point P to show the formation of its image.
(b) In the diagram, mark the position of eye to see the image.
(c) Is the image formed real or virtual? Explain why.

Answer
Diagram showing the image with the position of the eye marked is given below:

(c) The image formed is virtual because the reflected rays appear to meet only when they are produced backwards.
The diagram shown below shows an object XY in front of a plane mirror MM1. Draw on the diagram, path of two rays from each point X and Y of the object to show the formation of it's image.

Answer
Complete diagram showing the formation of the image is given below:

A ray is incident on a plane mirror. It's reflected ray is perpendicular to the incident ray. Find the angle of incidence.
Answer
According to the law of reflection,
angle of incidence = angle of reflection
i.e., i = r
Given,
Reflected ray is perpendicular to incident ray
Hence,
i + r = 90°
Using above law, we get,
i + i = 90°
2i = 90°
Hence,
i = r = 45°
Therefore, angle of incidence = 45°
A man standing in front of a plane mirror finds his image at a distance 6 metre from himself. What is the distance of a man from the mirror?
Answer
Given,
Distance between the man and his image is 6 m
But for a plane mirror,
object distance = image distance
Therefore,
Distance between the man and mirror = the distance between mirror and image
Hence,
the distance of the man and the mirror
An insect is sitting in front of a plane mirror at a distance 1 m from it.
(a) Where is the image of the insect formed?
(b) What is the distance between the insect and it's image?
Answer
(a) For a plane mirror, the image is as far behind the mirror as the object is in front of it i.e., the perpendicular distance of image from the mirror is equal to the perpendicular distance of object from the mirror.
Hence, the image of the insect is formed 1 m behind the mirror.
(b) The distance between the insect and it's image = the perpendicular distance of image from the mirror + the perpendicular distance of object from the mirror
= 1 + 1
= 2 m
Hence, the distance between the insect and it's image = 2 m
An object is kept at 60 cm in front of a plane mirror. If the mirror is now moved 25 cm away from the object, how does the image shift from it's previous position ?
Answer
Given,
Initially, the distance of the object A in front of plane mirror M is AM = 60 cm, therefore the image B is at a distance MB = 60 cm from the mirror M behind it. Distance between the object A and it's image B = 60 + 60 = 120 cm
On shifting the mirror by 25 cm away from the object, the new distance of object A from the mirror M' become AM' = 60 + 25 = 85 cm . The new image B' is now at a distance M'B' = 85 cm behind the mirror M'.
Hence, the current distance of the image from the object is 85 cm + 85 cm = 170 cm
Let the reference point be the position of the object,
So, the new distance of the image from the object - the distance of the image from the object initially = distance between the two positions of the image
Hence,
170 cm – 120 cm = 50 cm
Therefore,
the image shifts 50 cm from it's previous position.
An optician while testing the eyes of a patient keeps a chart of letters 3 m behind the patient and asks him to see the letters on the image of chart formed in a plane mirror kept at distance 2 m in front of him. At what distance is the chart seen by the patient?
Answer
Given,
Distance between the man and the mirror = 2 m
Distance between the man and the chart = 3 m
Therefore,
the distance between the chart and the mirror
= distance between the man and the mirror + distance between the man and the chart
= 3 m + 2 m
= 5 m
As the new image is formed on the mirror which is 2 m apart from the man,
So 5 m + 2 m = 7 m
Therefore,
the chart seen by the patient is 7 m away from him
In a barber's shop, two plane mirrors are placed :
- perpendicular to each other
- parallel to each other
- at an angle of 60° between them
- at an angle of 45° between them.
Answer
parallel to each other
Reason — In a barber's shop, in order to see the hairs at the back of the head two plane mirrors are placed parallel to each other at the front and at the back of the viewer.
For two mirrors kept parallel to each other, the number of images formed is :
- 5
- 7
- 0
- infinity
Answer
infinity
Reason — When two mirrors are kept parallel to each other, i.e., θ = 0 then n = = infinite. Hence, we get infinite number of images.
The number of images formed for two mirrors kept perpendicular to each other is :
- 1
- 2
- 3
- 5
Answer
3
Reason — When two mirrors are kept perpendicular to each other i.e., θ = 90°,
then n = = 4,
n = 4, is even so number of images is n - 1
Therefore,
n - 1
= 4 - 1
= 3
Hence, for two mirrors kept perpendicular to each other, three images are formed for an object kept in between them.
A thick plane mirror, silvered at its back, forms multiple number of images. Out of these, the brightest image is :
- first image
- second image
- third image
- All are of equal brightness
Answer
second image
Reason — A thick plane mirror forms a number of images due to multiple reflections within the glass from front surface and back reflecting surface. Out of these, the second image formed due to reflection from the back reflecting surface is the brightest.
How many plane mirrors are used in a periscope and kaleidoscope ?
- 2 and 3 respectively
- 3 each
- 3 and 2 respectively
- 2 and 4 respectively
Answer
2 and 3 respectively
Reason — In a periscope two parallel plane mirrors each inclined at 45° with the vertical walls are placed facing each other. In a kaleidoscope three plane mirrors inclined with each other at 60° are used.
In a kaleidoscope, three plane mirrors are inclined with each other at an angle of :
- 0°
- 30°
- 60°
- 90°
Answer
60°
Reason — In a kaleidoscope three plane mirrors inclined with each other at 60° are used.
In a periscope, two plane mirrors are inclined at an angle of ............... with the vertical walls.
- 0°
- 30°
- 45°
- 60°
Answer
45°
Reason — In a periscope two parallel plane mirrors each inclined at 45° with the vertical walls are placed facing each other.
Two mirrors are placed at right angles to each other as shown in the figure given below. A ray of light PQ strikes mirror OM at an angle of incidence 30°. What would be its angle of reflection from mirror ON ?
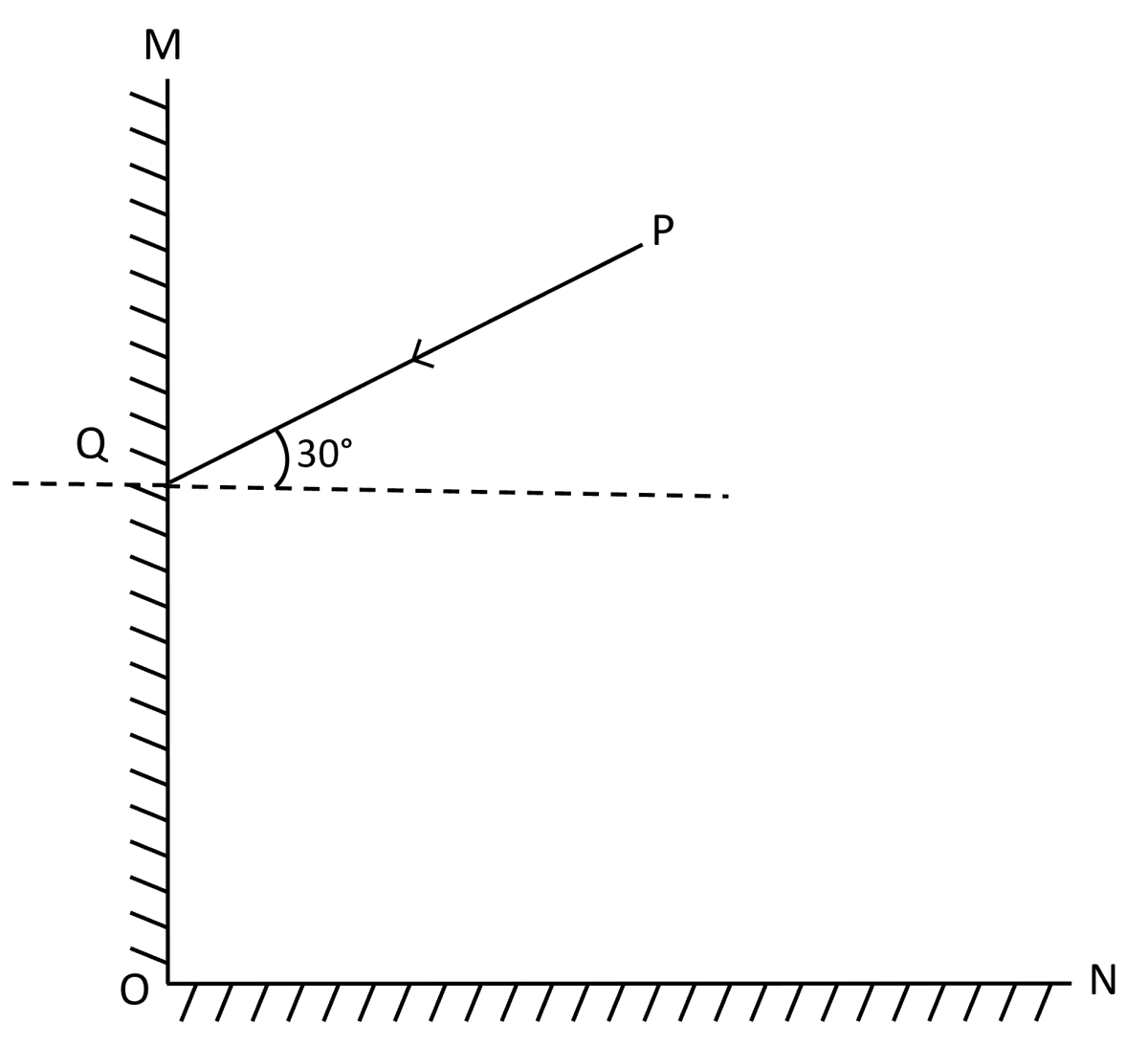
- 30°
- 60°
- 45°
- 90°
Answer
60°
Reason — From below figure,
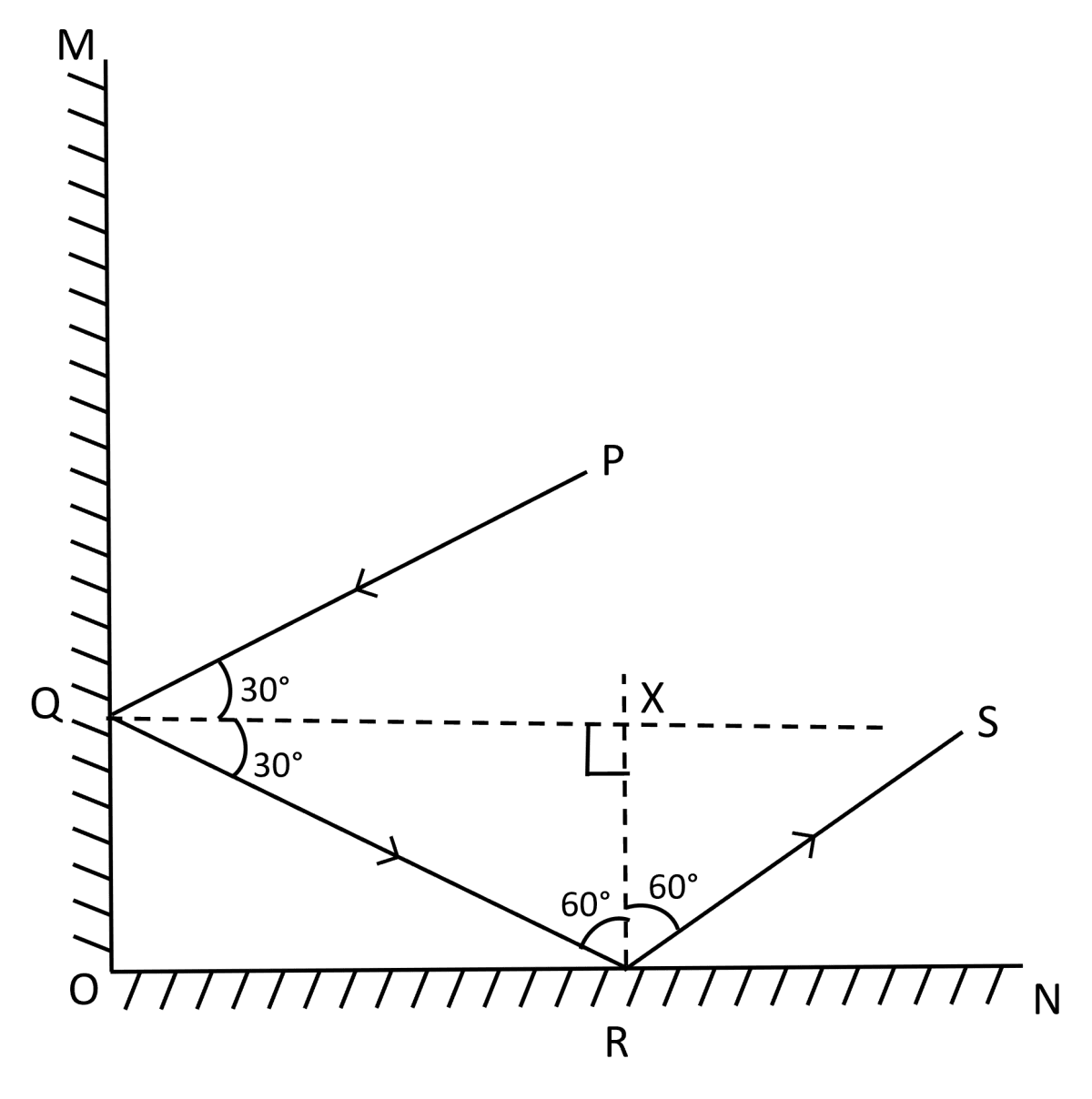
Reflection from mirror OM :
Angle of incidence = 30°,
So by law of reflection,
Angle of incidence = Angle of reflection = 30°
This means the reflected ray QR (say) makes an angle of 30° with the normal to OM, i.e., 60° with mirror OM. Now ray QR moves toward mirror ON, since OM and ON are at 90° and QR makes 60° with OM then it must make 90° - 60° = 30° with mirror ON.
So, angle between incident ray and normal to ON = 60°
⇒ Angle of incidence at ON = 60° = Angle of reflection
What is the most common use of a plane mirror ?
Answer
Looking glass.
How does an optician increase the effective length of his room by using a mirror ? Where does he place the sign board.
Answer
To increase the effective length of the optician's room, a plane mirror is placed on the front wall and the sign board is placed on the opposite wall, just behind the patient. With this arrangement, the sign board is at nearly double the length of the room for the patient.
What relationship do the images formed by two inclined plane mirrors have for their location with respect to the object placed between them ?
Answer
The images lie on the circumference of a circle whose centre lies at the point of intersection of the two mirrors and whose radius is equal to the distance of the object from the point of intersection
Two plane mirrors are placed making an angle θ in between them. Write an expression for the number of images formed if an object is placed in between the mirrors. State the condition, if any.
Answer
There are two cases possible:
Case 1 — If angle θ° between the mirrors is such that is odd:
- the number of images is n, when the object is placed asymmetrically between the mirrors.
- the number of images is n - 1, when the object is placed symmetrically (i.e., on the bisector of the angle) between the mirrors.
Case 2 — If is even, the number of images is always n - 1 for all positions of object in between the mirrors.
Two plane mirrors are placed making an angle θ° in between them. For an object placed in between the mirrors, if angle is gradually increased from 0° to 180°, how will the number of images change — increase, decrease or remain unchanged?
Answer
When two plane mirrors are placed making an angle θ° in between them and an object placed in between the mirrors, and the angle is gradually increased from 0° to 180°, then the number of images decreases.
State two uses of a plane mirror.
Answer
The uses of a plane mirror are —
(a) The most common and wide use is as a looking glass.
(b) In the optician's room to increase the effective length of the room. It is done by keeping a plane mirror on the front wall and the sign board on the opposite wall, just behind the patient. For the patient the sign board is at nearly double the length of the room.
How many images are formed for a point object kept in between the two plane mirrors at right angles to each other? Show them by drawing a ray diagram.
Answer
Three images will be formed when a point object is placed between two plane mirrors that are at right angles to each other.
The ray diagram is shown below:

Two plane mirrors are arranged parallel and facing each other at some separation. How many images are formed for a point object kept in between them? Show the formation of images with the help of a ray diagram.
Answer
Infinite number of images are formed when two plane mirrors are arranged parallel and facing each other at some separation.
Below ray diagram shows the formation of images:

State the number of images of an object placed between the two plane mirrors, formed in each case when the mirrors are inclined to each other at
(a) 90° and
(b) 60°
Answer
(a) When two mirrors are kept perpendicular to each other i.e., θ = 90°,
then n = = 4,
n = 4, is even so number of images is n - 1
Therefore,
n - 1
= 4 - 1
= 3
Hence, for two mirrors kept perpendicular to each other, three images are formed for an object kept in between them.
(b) When two mirrors are kept at 60° to each other,
then n = = 6
n = 6, is even so number of images is n - 1,
Therefore,
n - 1
= 6 - 1
= 5
Hence, for two mirrors kept at 60° to each other, five images are formed for an object kept in between them.
An object is placed (i) asymmetrically (ii) symmetrically, between two plane mirrors inclined at an angle of 50°. Find the number of images formed.
Answer
(i) When an object is placed asymmetrically between two plane mirrors inclined at an angle of 50° to each other then
(ii) The number of images formed when the object is placed symmetrically is n-1,
Hence,
7 - 1 = 6.
Therefore, 6 images will be formed when the object is placed symmetrically, between two plane mirrors inclined at an angle of 50°.
A ............... mirror is made by silvering the ............... surface of a piece of a hollow sphere.
- convex, outer
- plane, outer
- concave, outer
- concave, inner
Answer
concave, outer
Reason — A concave mirror is made by silvering the outer (or bulging) surface of a piece of a hollow sphere such that the reflection takes place from the hollow (or concave) surface.
A ............... mirror is made by silvering the ............... surface of a piece of a hollow sphere.
- concave, inner
- convex, inner
- convex, outer
- None of the above
Answer
convex, inner
Reason — A convex mirror is made by silvering the inner surface of a piece of a hollow sphere such that the reflection takes place from the outer (or bulging) surface.
The correct statement(s) is/are :
(i) The radius of a sphere of which the spherical mirror is a part is called the radius of curvature.
(ii) The geometric centre of the spherical surface of a mirror is called the centre of curvature.
(iii) Principal axis is the straight line joining the pole of the mirror to its aperture.
- (i)
- (ii)
- (iii)
- None of the above
Answer
(i)
Reason — The radius of a sphere of which the spherical mirror is a part is called the radius of curvature.
The geometric centre of the spherical surface of a mirror is called the pole of the mirror.
Principal axis is the straight line joining the pole of the mirror to its centre of curvature.
The focus of a concave mirror is a point on the ............... through which the light rays incident ............... to the principal axis pass after reflection from the mirror.
- centre of curvature, perpendicular
- principal axis, parallel
- principal axis, perpendicular
- aperture, parallel
Answer
principal axis, parallel
Reason — The focus of a concave mirror is a point on the principal axis through which the light rays incident parallel to the principal axis, pass after reflection from the mirror.

For an incident ray directed towards center of curvature of a spherical mirror, the reflected ray:
- retraces it's path
- passes through the focus
- passes through the pole
- becomes parallel to the principal axis
Answer
retraces it's path
Reason — A line joining the centre of curvature to any point on the surface of mirror is normal to the mirror at that point, so a ray AD passing through the center of curvature C (or appearing to pass through through the centre of curvature C) is incident normally on the spherical mirror.
Since it's angle of incidence is zero, therefore the angle of reflection will also be zero and the ray AD gets reflected along it's own path DA as shown below.

A ray either incident from the focus (or converging at the focus), after reflection from a spherical mirror :
- becomes perpendicular to the principal axis
- becomes parallel to the principal axis
- becomes normal to the focus
- passes through the centre of curvature
Answer
becomes parallel to the principal axis
Reason — A ray either incident from the focus (or converging at the focus), after reflection from a spherical mirror becomes parallel to the principal axis.
For a concave mirror, when the object is at infinity, the nature of the image formed at focus is
- virtual, inverted
- virtual, diminished to a point
- real, enlarged, inverted
- real, inverted, diminished to a point
Answer
real, inverted, diminished to a point
Reason — For a concave mirror, when the object is at infinity, the nature of the image formed at focus is real, inverted, diminished to a point.

For a concave mirror, when the object is at the centre of curvature, the place and nature of the image formed is :
- at focus, real, inverted
- at focus, virtual, inverted
- at centre of curvature, real, inverted, diminished
- at centre of curvature, real, same size as that of the object
Answer
at centre of curvature, real, same size as that of the object
Reason — For a concave mirror, when the object is at the centre of curvature, the image is also at the centre of curvature. It is real and same size as that of the object.
For a concave mirror, when the object is at focus, the size of the image formed is:
- magnified
- highly magnified
- diminished
- of the same size
Answer
highly magnified
Reason — For a concave mirror, when the object is at focus, the image is at infinity. It is real, inverted and highly magnified.
The image formed by a convex mirror is:
- erect and diminished
- erect and enlarged
- inverted and diminished
- inverted and enlarged
Answer
erect and diminished
Reason — In a convex mirror, the image formed is always virtual, erect and diminished. It is always situated between it's pole and focus irrespective of the distance of object in front of the mirror.
For a convex mirror, when the object is in front of the mirror, the image formed is :
- real, upright and magnified
- real, inverted and diminished
- virtual, upright and magnified
- virtual, upright and diminished
Answer
virtual, upright and diminished
Reason — For a convex mirror, when the object is in front of the mirror, the image is between the pole and the focus. It is virtual, upright and diminished.

The wrong rule of sign convention is :
(i) All distances are measured from the centre of curvature of the mirror taken as origin.
(ii) The distances measured along the principal axis in the direction of incident light are positive.
(iii) The distances above the principal axis are taken positive.
- (i)
- (ii)
- (iii)
- both (i) and (ii)
Answer
(i)
Reason — The rules of sign convention are :
(i) All distances are measured from the pole of the mirror taken as origin.
(ii) The distances measured along the principal axis in the direction of incident light are positive while those opposite to the incident light are negative.
(iii) The distances above the principal axis are taken positive and those below the principal axis are taken negative.
For a convex mirror, the value of u is always ............... and the value of v is ...............
- positive, positive
- positive, negative
- negative, negative
- negative, positive
Answer
negative, positive
Reason — For a convex mirror, the value of u is always negative and the value of v is always positive.
A real and enlarged image can be obtained by using a:
- convex mirror
- plane mirror
- concave mirror
- either convex or plane mirror
Answer
concave mirror
Reason — The image formed by a concave mirror is real and enlarged, when the object is between centre of curvature and focus or at focus.
The type of mirror used as a reflector in the street lights is :
- plane mirror
- convex mirror
- concave mirror
- parabolic mirror
Answer
convex mirror
Reason — A convex polished metallic surface is used in street lamps as a reflector so as to diverge light over a larger area.
The type of mirror used as a shaving mirror in daily life is :
- plane mirror
- convex mirror
- concave mirror
- parabolic mirror
Answer
concave mirror
Reason — When a concave mirror is held near the face (such that the face is between pole and focus of the mirror), it gives an upright and magnified image. Hence even tiny hair can be seen. For this concave mirror of large focal length and large aperture is used.
Which mirror always forms a diminished image for all positions of the object placed in front of it ?
- plane mirror
- convex mirror
- concave mirror
- parabolic mirror
Answer
convex mirror
Reason — A convex mirror always forms a diminished image for all positions of the object placed in front of it.
The figure shows the image of a clock as seen in the plane mirror. The correct time is :
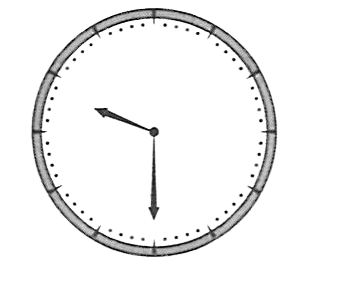
- 4:30
- 6:30
- 2:30
- 3:30
Answer
2:30
Reason — As the mirror image of the clock shows that hour hand is pointing slightly past 9 and minute hand at 6 (i.e., 30 minutes) so the mirror image shows 9:30. Since a plane mirror always produces laterally inverted images so in this case the hour hand should actually point slightly past 2 and minute hand will suffer no inversion due to symmetry so the clock will show 2:30.
We use a concave polished metallic surface as a reflector in a torch to obtain a parallel beam of light. The position of the bulb is :
- at the centre of curvature of the reflector.
- at the focus of the reflector
- between the focus and centre of curvature of the reflector
- can be any of the above options
Answer
at the focus of the reflector
Reason — In a torch, we want the light rays to come out as a parallel beam as this helps the light travel a long distance in a specific direction and a concave mirror reflects light rays parallel to the principal axis if the source is placed at its focus.
So, if we want a parallel beam of light (which is the case in a torch), the bulb should be placed at the focus of the concave mirror.
Assertion (A) : For a ray of light incident at an angle of incidence i = 0°, angle of reflection is r = 0°.
Reason (R) : The angle of incidence i is equal to angle of reflection r.
- both A and R are true and R is the correct explanation of A
- both A and R are true and R is not the correct explanation of A
- assertion is false but reason is true
- assertion is true but reason is false
Answer
both A and R are true and R is the correct explanation of A
Explanation
Assertion (A) is true because if a ray of light hits the mirror perpendicularly (i.e., along the normal), the angle of incidence is 0°, and the ray reflects back along the same path. So, angle of reflection is also 0°.
Reason (R) is true because it's a law of reflection which states that during reflection, angle of incidence is always equal to angle of reflection so the Reason correctly explains the Assertion.
Assertion (A) : The image of an object placed close to a concave mirror is a real image.
Reason (R) : A real image is formed due to the actual intersection of the reflected rays.
- both A and R are true and R is the correct explanation of A
- both A and R are true and R is not the correct explanation of A
- assertion is false but reason is true
- assertion is true but reason is false
Answer
assertion is false but reason is true
Explanation
Assertion (A) is false because when an object is placed close to a concave mirror, i.e., between the pole (P) and the focus (F), the image formed is virtual, erect, and magnified, not real and only when the object is placed beyond the focus, the image formed is real and inverted.
Reason (R) is true because this is the definition of a real image which is formed when reflected rays actually meet.
Assertion (A) : For a real image formed by a spherical mirror, linear magnification (m) is positive.
Reason (R) : Both u and v are negative for a real image.
- both A and R are true and R is the correct explanation of A
- both A and R are true and R is not the correct explanation of A
- assertion is false but reason is true
- assertion is true but reason is false
Answer
assertion is false but reason is true
Explanation
Only a concave mirror can form a real image; convex mirrors cannot.
For a real image formed by a concave mirror:
- Both and are negative.
- Magnification is negative, showing the image is inverted.
So the assertion is false (m is negative), but the reason is true (both distances are negative).
Assertion (A) : For an object placed symmetrically when the angle θ between the mirrors is 72°, the number of images formed is 4.
Reason (R) : If n = 360°/θ is odd, the number of images for an object placed symmetrically is equal to n.
- both A and R are true and R is the correct explanation of A
- both A and R are true and R is not the correct explanation of A
- assertion is false but reason is true
- assertion is true but reason is false
Answer
assertion is true but reason is false
Explanation
Assertion (A) is true because as
Where:
θ = angle between the mirrors
n = number of images formed (if object is placed symmetrically)
Substitute, θ = 72° :
Reason (R) is false because if angle θ° between the mirrors is such that is odd, then
(i) the number of images is n, when the object is placed asymmetrically between the mirrors.
(ii) the number of images is n - 1, when the object is placed symmetrically (i.e., on the bisector of the angle) between the mirrors.
Assertion (A) : Concave mirror is used as doctor's head mirror.
Reason (R) : If a parallel beam of light is incident on a concave mirror, the mirror focuses the beam to a point.
- both A and R are true and R is the correct explanation of A
- both A and R are true and R is not the correct explanation of A
- assertion is false but reason is true
- assertion is true but reason is false
Answer
both A and R are true and R is the correct explanation of A
Explanation
Assertion (A) is true: A concave mirror is used as a doctor's head mirror because it can direct and concentrate light into the patient’s body parts (such as teeth, nose, throat, ear, etc.) for better visibility.
Reason is true: When a parallel beam of light (like light from a lamp) falls on a concave mirror, the mirror reflects and converges the rays to its focal point, producing a bright, concentrated spot of light.
This property of focusing parallel rays to a point is precisely why concave mirrors are used in head mirrors, as it enables the doctor to project an intense beam exactly where it is needed. Therefore, the reason correctly explains the assertion.
Assertion (A) : A student is given a spherical mirror of focal length -10 cm. He identifies it as a concave mirror.
Reason (R) : Focal length of a concave mirror is always positive.
- both A and R are true and R is the correct explanation of A
- both A and R are true and R is not the correct explanation of A
- assertion is false but reason is true
- assertion is true but reason is false
Answer
assertion is true but reason is false
Explanation
Assertion (A) is true because according to sign conventions (the mirror formula uses the Cartesian system), the focal length of a concave mirror is negative. So, a mirror with focal length –10 cm is indeed a concave mirror.
Reason (R) is false because the focal length of a concave mirror is always negative in mirror formula sign convention.
What is a spherical mirror?
Answer
A reflecting surface which is a part of a sphere is called a spherical mirror.
Define centre of curvature of a spherical mirror.
Answer
The centre of curvature of a mirror is the centre of the sphere of which the mirror is a part.
Define radius of curvature of a spherical mirror.
Answer
The radius of the sphere of which the spherical mirror is a part, is called the radius of curvature of the mirror.
What is the aperture of a spherical mirror ?
Answer
The plane surface area of the mirror through which light rays enter and fall on the mirror is called its aperture.
Define the pole of a spherical mirror.
Answer
The geometric centre of the spherical surface of mirror is called the pole of the mirror.
Name the spherical mirror which always produces an erect and virtual image. How is the size of image related to the size of object?
Answer
A convex mirror always produces an erect and virtual image. The size of the image is shorter than the size of the object.
(a) For what position of object, the image formed by a concave mirror is magnified and erect?
(b) State whether the image in part (a) is real or virtual?
Answer
(a) When the object is between the pole and focus of a concave mirror then the image formed is magnified and erect
(b) The image is virtual.
(a) State the position of object for which the image formed by a concave mirror is of same size.
(b) Write two more characteristics of the image.
Answer
(a) When the object is at the centre of curvature of a concave mirror, the image is of the same size as the object.
(b) The images thus formed is real and inverted.
(a) What is a real image?
(b) What type of mirror can be used to obtain a real image of an object?
(c) Does the mirror mentioned in part (b) form real image for all locations of the object?
Answer
(a) A real image is one that can be obtained on a screen.
(b) A concave mirror can be used to obtain a real image of an object.
(c) No, concave mirror does not form real image for all the locations of the object.
Name the kind of mirror used to obtain —
(a) a real and enlarged image,
(b) a virtual and enlarged image,
(c) a virtual and diminished image,
(d) a real and diminished image.
Answer
(a) Concave mirror is used to obtain a real and enlarged image.
(b) Concave mirror is used to obtain a virtual and enlarged image.
(c) Convex mirror is used to obtain a virtual and diminished image.
(d) Concave mirror is used to obtain a real and diminished image.
How is the focal length of a spherical mirror related to it's radius of curvature?
Answer
The focal length 'f' is related to the radius of curvature 'R' in the following way —
Write the spherical mirror's formula and explain the meaning of each symbol used in it.
Answer
The formula for the spherical mirror is —
u = distance of object
v = distance of image
f = focal length
State the kind of mirror used —
(a) by a dentist,
(b) as a search-light reflector.
Answer
(a) Concave mirror is used by a dentist.
(b) Concave mirror is used as a search-light reflector.
Which mirror will you prefer to use as a rear view mirror in a car — plane mirror or convex mirror? Give one reason.
Answer
A convex mirror would be preferred in comparison to a plane mirror for use as a rear view mirror in a car because it provides a much wider field view as compared to a plane mirror of the same size. The below ray diagram shows this:

How is magnification (m) related to the distance of the object (u) and the distance of the image (v) ?
Answer
where
'I' is the length of the image,
'O' is the length of the object,
'v' is the distance of the image,
'u' is the distance of the object.
Name the two kinds of spherical mirrors and distinguish between them.
Answer
Depending on whether the inner or outer surface of the sphere is silvered, spherical mirrors are of two types —
- Concave mirror
- Convex mirror
Difference between the two mirrors are —
| Concave mirror | Convex mirror |
|---|---|
| It is made by silvering the outer surface of a part of the hollow sphere, so reflection takes place from the inner surface. | It is made by silvering the inner surface of a part of the hollow sphere, so reflection takes place from the bulging surface. |
| The light rays incident on it converge after reflection. | The light rays incident on it diverge after reflection. |
| The image formed by it is real as well as virtual. For all positions of the object at or beyond the focus, the image is real, while for positions of the object between the focus and the pole, the image is virtual. | The image formed by it is always virtual for all positions of the object infront of it. |
| For object away from the centre of curvature, the image is diminished, for object at the centre of curvature, image is of same size and for object within the centre of curvature, image is diminished. | The image is always diminished for all positions of the object infront of it. |
Define the terms pole, principal axis and center of curvature with reference to a spherical mirror.
Answer
Pole — The geometric centre of the spherical surface of mirror is called the pole of the mirror.
Principal axis — It is the straight line joining the pole of the mirror to it's centre of curvature.
Centre of curvature — The centre of curvature of a mirror is the centre of sphere of which the mirror is a part.
Name the spherical mirror which (i) diverges (ii) converges the beam of light incident on it. Justify your answer by drawing a ray diagram in each case.
Answer
(i) A convex mirror diverges a beam of light incident on it.
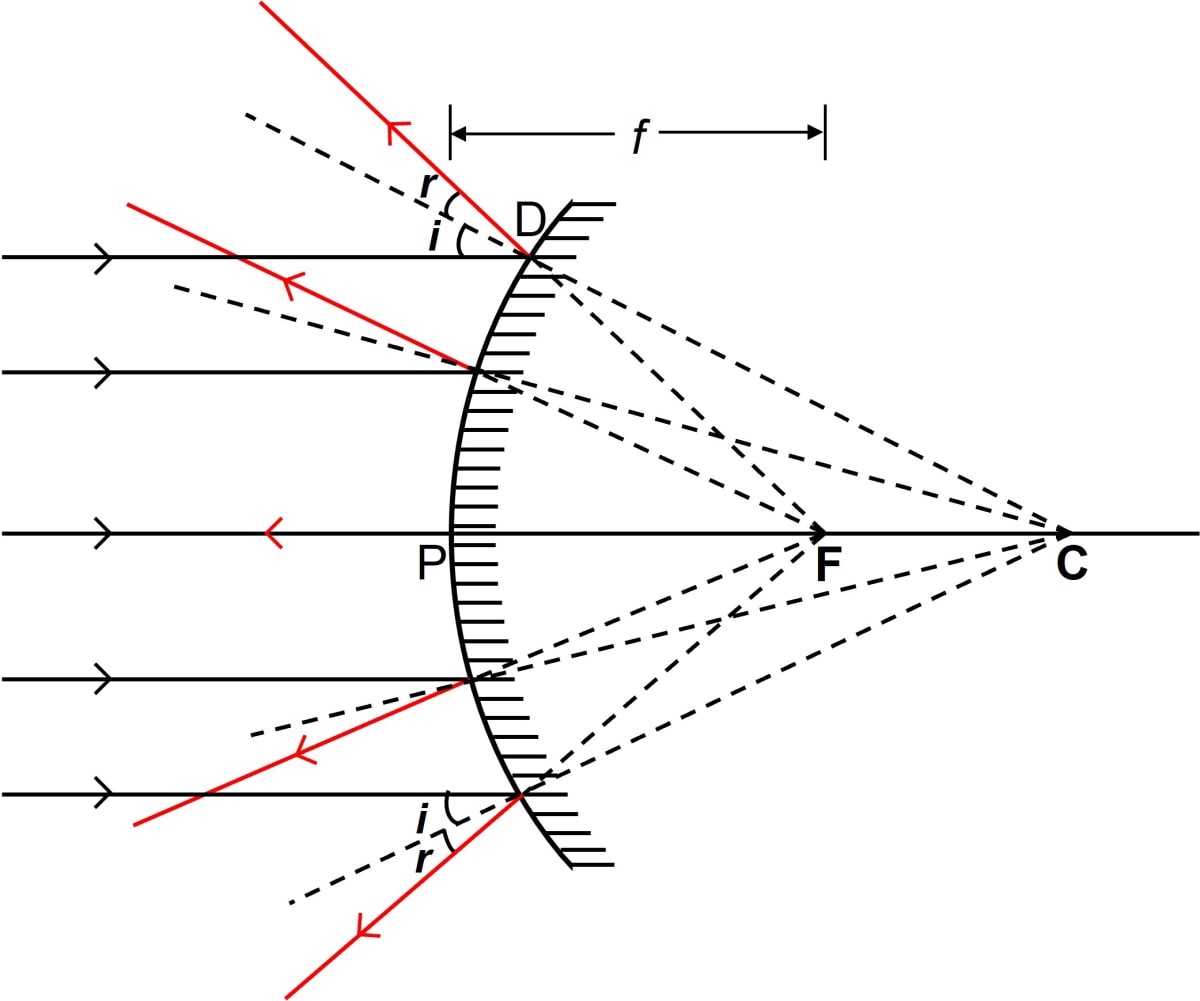
(ii) A concave mirror converges a beam of light incident on it.

Define the terms focus and focal length of a concave mirror. Draw diagram to illustrate your answer.
Answer
Focus of a concave mirror — The focus of a concave mirror is a point on the principal axis through which the light rays incident parallel to the principal axis, pass after reflection from the mirror.

Focal length of a concave mirror — The distance of focus F from the pole P of the mirror is called the focal length of the mirror.
i.e., focal length f = PF.
State the direction of incident ray which after reflection from a spherical mirror retraces it's path. Give a reason to your answer.
Answer
When the incident ray is directed towards the centre of curvature, after reflection from a spherical mirror, it retraces it's path.
It is because the ray is normal to the spherical mirror, so ∠i (angle of incidence) = 0, therefore, ∠r (angle of reflection) = 0.
What is meant by magnification? Write it's expression. What is it's sign for the (a) real (b) virtual, image?
Answer
The ratio of length of the image to the length of object, is called linear magnification.
where
'I' is the length of the image,
'O' is the length of the object,
'v' is the distance of the image,
'u' is the distance of the object.
(a) For a real image, linear magnification m is negative.
(b) For a virtual image, linear magnification m is positive.
Upto what maximum distance from the pole, the image in a convex mirror can be obtained ? What will be the location of object then ?
Answer
The maximum distance from the pole, in a convex mirror where the image can be obtained is till the focal length of the mirror. The object would then has to be at infinity.
Upto what maximum distance from a concave mirror, the image can be obtained? What will be the location of object for it?
Answer
The maximum distance from the concave mirror, where the image can be obtained is infinity. The object would then be at focus.
How will you distinguish between a plane mirror, a concave mirror and a convex mirror, without touching them?
Answer
In order to distinguish between a plane mirror, a concave mirror and a convex mirror, the given mirror is held near the face and the image obtained is seen.
There can be the following three cases —
Case 1 — If image is upright, of same size and it does not change in size by moving the mirror towards or away from the face, then the mirror is plane.
Case 2 — If image is upright, magnified and increases in size on small movement of the mirror away from the face then the mirror is concave.
Case 3 — If image is upright, dimished and decreases in size on small movement of the mirror away from the face then the mirror is convex.
State two uses of a concave mirror.
Answer
Uses of a concave mirror are as follows —
- As a shaving mirror — When a concave mirror is held near the face (such that the face is between pole and focus of the mirror), it gives an upright and magnified image. Hence even tiny hair can be seen.
- As a reflector — In torch, searchlight and head light of automobiles, cycles etc., a concave polished metallic surface is used to obtain a parallel beam of light.
(a) When a concave mirror is used as a shaving mirror, where is the person's face in relation to the focus of mirror?
(b) State three characteristics of the image seen in part (a)
Answer
(a) When a concave mirror is used as a shaving mirror, the person's face should be between the pole and the focus.
(b) The image formed is erect, virtual and magnified.
Draw suitable diagrams to illustrate the action of (i) concave mirror, and (ii) convex mirror, on a beam of light incident parallel to the principal axis.
Answer
(i) Below ray diagram illustrates the action of concave mirror on a beam of light incident parallel to the principal axis:

(ii) Below ray diagram illustrates the action of convex mirror on a beam of light incident parallel to the principal axis:

Explain the meaning of the terms focus and focal length in case of a convex mirror, with the help of a suitable ray diagram.
Answer
Focus of a convex mirror — The focus of a convex mirror is a point on the principal axis from which, the light rays that are incident parallel to the principal axis, appear to come, after reflection from the mirror.

Focal length of a concave mirror — The distance of focus F from the pole P of the mirror is called the focal length of the mirror.
i.e., focal length f = PF.
(i) Name the mirrors shown in figure (a) and (b).
(ii) In each case (a) and (b), draw the reflected rays for the given incident rays and mark focus by the symbol F.

Answer
(i) The figure (a) shows convex mirror and figure (b) shows concave mirror.
(ii) Diagrams showing reflected rays are shown below:
(a)

(b)

Complete the following diagrams in figure by drawing the reflected rays for the incident rays 1 and 2.

Answer
Below are the completed diagrams showing the reflected rays for the incident rays 1 and 2:
(a)

(b)

Complete the following diagrams shown in figure by drawing the reflected ray for each of the incident ray A and B.

Answer
Below are the completed diagrams showing the reflected rays for the incident rays A and B:
(a)

(b)

State the two convenient rays that are chosen to construct the image by a spherical mirror for a given object? Explain your answer with the help of suitable ray diagrams.
Answer
The two convenient rays, chosen to construct the image by a spherical mirror are —
(i) A ray that passes through the center of curvature.
A line joining the centre of curvature to any point on the surface of mirror is normal to the mirror at that point, therefore a ray AD passing through the center of curvature C (or appearing to pass through through the centre of curvature C) is incident normally on the spherical mirror.
Since it's angle of incidence is zero, therefore the angle of reflection will also be zero and the ray AD gets reflected along it's own path DA as shown below:

(ii) A ray parallel to the principal axis.
A ray of light AD incident parallel to the principal axis, after reflection passes either through the focus F(in a concave mirror) or will appear to come from the focus F (in a convex mirror) along DB as shown below:

Figure shows a concave mirror with it's pole at P, focus F and center of curvature C. Draw ray diagram to show the formation of image of an object OA.

Answer
Ray diagram showing the formation of the image is given below:

Figure shows a concave mirror with it's pole at P, focus F and center of curvature C. Draw ray diagram to show the formation of image of an object OA.

Answer
Ray diagram showing the formation of the image is given below:

The diagram below in figure shows a convex mirror. C is it's center of curvature and F is it's focus. (i) Draw two rays from A and hence locate the position of image of object OA. Label the image IB. (ii) State three characteristics of the image.

Answer
(i) Below completed ray diagram shows the position of the image of object OA:

(ii) The three characteristics of the image are virtual, upright and diminished.
Draw a ray diagram to show the formation of image by a concave mirror for an object placed between it's pole and focus. State three characteristics of the image.
Answer
Below is the ray diagram showing the formation of image by a concave mirror for an object placed between it's pole and focus:

When the object is between the focus F and the pole P, the image is formed behind the mirror. It is virtual, upright and magnified.
Draw a ray diagram to show the formation of image by a concave mirror for an object beyond it's center of curvature. State three characteristics of the image.
Answer
The image by a concave mirror for an object beyond it's center of curvature is shown below:

When object is beyond the centre of curvature C, the image is between the focus F and the centre of curvature C. It is real, inverted and diminished.
Draw a ray diagram to show the formation of image of an object kept in front of a convex mirror. State three characteristics of the image.
Answer
The diagram below shows the formation of image when the object is kept in front of a convex mirror.

When the object is in in front of the convex mirror, the image is between the pole P and focus F on the other side of the mirror.
The image formed is virtual, upright and diminished.
Discuss the position and nature of image formed by a concave mirror when an object is moved from infinity towards the pole of mirror.
Answer
The image formed moves away from the concave mirror when an object is moved from infinity towards the pole of mirror.
The image is diminished when the object is beyond centre of curvature, but it becomes magnified as the object comes within the centre of curvature. The image is of the same size of the object when the object is at the centre of curvature.
For the object situated beyond focus, the image is always real and inverted, whereas for the object situated between the focus and pole the image is upright and virtual.
The table below shows the position, size and nature of the image formed by a concave mirror for different positions of the object.
| No. | Position of the object | Position of the image | Size of the image | Nature of the image |
|---|---|---|---|---|
| 1 | At infinity | At the focus | Diminished to a point | Real and inverted |
| 2 | At very far distance | In focal plane | Highly diminished | Real and inverted |
| 3 | Beyond the centre of curvature | Between the centre of curvature and focus | Diminished | Real and inverted |
| 4 | At the centre of curvature | At the centre of curvature | Same size | Real and inverted |
| 5 | Between the centre of curvature and focus | Beyond the centre of curvature | Magnified | Real and inverted |
| 6 | At focus | At infinity | Highly magnified | Real and inverted |
| 7 | Between the focus and the pole | Behind the mirror | Magnified | Virtual and upright |
Discuss the position and nature of image formed by a convex mirror when an object is moved from infinity towards the pole of mirror.
Answer
In a convex mirror, the image formed is always virtual, upright and diminished. It is always situated between it's pole and focus irrespective of the distance of object in front of the mirror.
As the object comes closer to the mirror from infinity towards the pole, it's image shifts from focus towards the pole and increase in size.
The table below shows the position, size and nature of the image formed by a convex mirror
| No. | Position of the object | Position of the image | Size of the image | Nature of the image |
|---|---|---|---|---|
| 1. | At infinity | At focus | Diminished to a point | Virtual and upright |
| 2. | At any other point | Between focus and the pole | Diminished | Virtual and upright |
Why does a driver use a convex mirror instead of a plane mirror as a rear view mirror? Illustrate your answer with the help of a ray diagram.
Answer
A convex mirror diverges the incident light beam and always forms a virtual, small and erect image behind the mirror between it's pole and focus. This fact enables the driver to use it as a rear view mirror in vehicles to see all the traffic approaching from behind.
Although a plane mirror can also be used as a rear view mirror, but a convex mirror provides a much wider field view as compared to a plane mirror of the same size.
The below diagram shows how a convex mirror provides a better field view than a plane mirror.

The radius of curvature of a convex mirror is 40 cm. find it's focal length.
Answer
Focal length = x Radius of curvature
Given,
R = 40 cm
Substituting the values in the formula above we get,
Hence, focal length of the convex mirror = 20 cm.
The focal length of a concave mirror is 10 cm. Find it's radius of curvature.
Answer
Focal length = x Radius of curvature
Given,
f = 10 cm
Substituting the values in the formula above we get,
Hence, radius of curvature of concave mirror = 20 cm.
An object of height 2 cm is placed at a distance 20 cm in front of a concave mirror of focal length 12 cm. Find the position, size and nature of the image.
Answer
Given,
Object height (O) = 2 cm
Focal length (f) = 12 cm (negative)
Object distance (u) = 20 cm (negative)
Mirror formula:
Substituting the values in the formula above we get,
Hence, the image is formed at a distance of 30 cm in front of the mirror.
Hence, length of image = 3 cm
Image will be real, inverted and magnified.
An object is placed at 4 cm distance in front of a concave mirror of radius of curvature 24 cm. Find the position of image. Is the image magnified?
Answer
Given,
Radius of curvature (R) = 24 cm (negative)
Object distance (u) = 4 cm (negative)
Focal length = x Radius of curvature
Substituting the values in the formula above, we get,
Hence, focal length of the concave mirror = -12 cm.
Mirror formula:
Now, substituting the values in the mirror formula , we get,
The image is formed 6 cm behind the mirror.
Computing linear magnification:
As, the length of image is 1.5 times the image of object, hence, the image is magnified.
At what distance from a concave mirror of focal length 25 cm should an object be placed so that the size of image is equal to the size of the object.
Answer
To get an image of same size the object should be placed at the center of the curvature of a concave mirror.
Given,
focal length = 25 cm
As, centre of curvature = 2 x focal length
Therefore,
centre of curvature
= 2 x 25
= 50 cm
Hence, the object should be kept at 50 cm so that the size of image is equal to the size of object.
An object 5 cm high is placed at a distance 60 cm in front of a concave mirror of focal length 10 cm. Find (i) the position and (ii) size, of the image.
Answer
Given,
Object height (O) = 5 cm
focal length (f) = 10 cm (negative)
Object distance (u) = 60 cm (negative)
Mirror formula:
Substituting the values in the formula above, we get,
The image distance (v) = 12 cm infront of the mirror.
Hence, length of image = 1 cm
Negative sign shows that the image will be inverted.
A point light source is kept in front of a convex mirror at a distance of 40 cm. The focal length of the mirror is 40 cm. Find the position of image.
Answer
Given,
u = 40 cm (negative)
f = 40 cm (positive)
Mirror formula:
Substituting the values in the formula above, we get,
Hence, the image is formed 20 cm behind the mirror.
When an object of height 1 cm is kept at a distance 4 cm from a concave mirror, it's erect image of height 1.5 cm is formed at a distance 6 cm behind the mirror. Find the focal length of the mirror.
Answer
Given,
u = 4 cm (negative)
v = 6 cm (positive)
Mirror formula:
Substituting the values in the formula above, we get,
Hence, the focal length of concave mirror = 12 cm
An object of length 4 cm is placed in front of a concave mirror at a distance 30 cm. The focal length of mirror is 15 cm. (a) Where will the image form? (b) What will be the length of image?
Answer
(a) Given,
u = 30 cm (negative)
f = 15 cm (negative)
Mirror formula:
Substituting the values in the formula above, we get,
Hence, the image is formed at 30 cm in front of the mirror
(b) Magnification
Hence, length of image = 4 cm
Negative sign represents that the image is inverted.
A concave mirror forms a real image of an object placed in front of it at a distance 30 cm, of size three times the size of object. Find (a) the focal length of mirror (b) position of image.
Answer
Given,
(a) Distance of the object (u) = 30 cm (negative)
Image height = 3 times the height of object
So, magnification (m) = 3 (negative for the real image)
Hence, the image is formed 90 cm in front of the mirror.
Mirror formula:
Substituting the values in the mirror formula we get,
Hence, focal length of the mirror = 22.5 cm
(b) The image is formed 90 cm in front of the mirror
A concave mirror forms a virtual image of size twice that of the object placed at a distance 5 cm from it. Find (a) the focal length of the mirror (b) position of the image.
Answer
(a) Given,
Distance of the object (u) = 5 cm (negative)
Magnification (m) = 2 (positive for the virtual image)
Hence, the image is formed 10 cm behind the mirror.
Mirror formula:
Substituting the values in the mirror formula, we get,
Hence, focal length of the mirror = 10 cm
(b) The position of the image is 10 cm behind the mirror
The image formed by a convex mirror is of size one-third the size of object. How are u and v related?
Answer
Magnification (m) = - = -
Hence, we get,
v = - u
Or
u = -3v
The erect image formed by a concave mirror is of size double the size of object. How are u and v related?
Answer
Magnification (m) = -
Given,
2 = -
Hence, v = -2u
The magnification for a mirror is -3. How are u and v related?
Answer
Magnification (m) = -
Given,
Hence, v = 3u