Measurements and Experimentation

Exercise 1(A) — Multiple Choice Type

Question 1

The condition(s) essential for a unit to be accepted internationally :

1. The unit should be of convenient size and without any ambiguity.
2. The unit should be reproducible.
3. The value of the unit should not change with space and time.
4. All of the above.

Answer

All of the above

Reason — The condition(s) essential for a unit to be accepted internationally are :

1. The unit should be of convenient size.
2. It should be possible to define the unit without any ambiguity.
3. The unit should be reproducible.
4. The value of unit should not change with space and time.

Question 2

In mechanics, the three fundamental quantities are:

1. Length, mass, velocity
2. Mass, time, density
3. Mass, time, pressure
4. Length, mass, time

Answer

Length, mass, time

Reason — In mechanics, length, mass and time are the three fundamental units. Unit of length is metre (m), unit of mass is kilogram (kg), unit of time is second (s).

Question 3

How many units are fundamental and complementary?

1. 2 fundamental, 7 complementary
2. 3 fundamental, 6 complementary
3. 7 fundamental, 2 complementary
4. 4 fundamental, 5 complementary

Answer

7 fundamental, 2 complementary

Reason — Fundamental and complementary units are as follows:

Question 4

The fundamental unit is —

1. newton
2. pascal
3. hertz
4. second

Answer

second

Reason — Out of the given units, only 'second' is a fundamental unit.

Question 5

Which of the following unit is not a fundamental unit:

1. Metre
2. Litre
3. Second
4. Kilogram

Answer

Litre

Reason — Metre, second and kilogram are the fundamental units whereas litre is a derived unit.

Question 6

One millimeter is ............... part of a metre:

1. One hundredth
2. One thousandth
3. One billionth
4. One millionth

Answer

One thousandth

Reason — One millimeter is one thousandth part of a metre.

1 mm = $\dfrac{1}{1000}$ m = 10^-3 m = $\dfrac{1}{10}$ cm

Question 7

One astronomical unit is equal to:

1. 1.496 x 10¹¹ metre
2. 1.596 x 10¹² metre
3. 1.498 x 10¹⁰ metre
4. 1.398 x 10¹¹ metre

Answer

1.496 x 10¹¹ metre

Reason — One astronomical unit is equal to the mean distance between the earth and the sun. i.e.,

1 A.U. = 1.496 x 10¹¹ metre

Question 8

The distance of stars from earth is generally measured in:

1. Kilometre
2. Light year
3. Angstrom
4. Fermi

Answer

Light year

Reason — A light year is the distance travelled by light in vacuum, in one year.

Question 9

1 Fermi is equal to:

1. 10^-14 m
2. 10^-10 m
3. 10¹⁵ m
4. 10^-15 m

Answer

10^-15 m

Reason — Fermi is 10^-15th part of a metre. i.e., 1 fermi = 10^-15 m

Question 10

The unit of time is:

1. light year
2. parsec
3. leap year
4. angstrom

Answer

leap year

Reason — Leap year is the unit of time. Light year, parsec, angstrom are unit of distance. A leap year is the year in which the month of February is of 29 days.

Question 11

1 Å is equal to:

1. 0.1 nm
2. 10^-10cm
3. 10^-8m
4. 10⁴µ

Answer

0.1 nm

Reason — 10 Å = 1nm
∴ 1 Å = 0.1nm

Question 12

One metric tonne is equal to :

1. 10 quintal
2. 100 quintal
3. 1000 quintal
4. 25 quintal

Answer

10 quintal

Reason — It is one thousand times a kilogram. i.e., 1 metric tonne = 1000 kg = 10 quintal.

Question 13

Light-year is the unit of:

1. Time
2. Length
3. Mass
4. none of these

Answer

Length

Reason — A Light-year is the distance travelled by light in vacuum, in one year.

Question 14

One solar mass is equal to :

1. 3 x 10²⁰ kg
2. 2 x 10²⁷ kg
3. 2 x 10³⁰ kg
4. 3 x 10³⁰ kg

Answer

2 x 10³⁰ kg

Reason — The mass of large heavenly bodies is measured in terms of solar mass where 1 solar mass is the mass of the sun i.e., 1 solar mass = 2 x 10³⁰ kg

Question 15

One lunar cycle is nearly equal to:

1. 28.5 days
2. 29.5 days
3. 30 days
4. 30.5 days

Answer

29.5 days

Reason — One lunar cycle is the amount of time it takes for the Moon to complete one orbit around the Earth and it is nearly equal to 29.5 days.

Question 16

One shake is equal to:

1. 10^-9 s
2. 10^-8 s
3. 10^-10 s
4. 10⁸ s

Answer

10^-8 s

Reason — Shake is a smaller unit of time where, 1 shake = 10^-8 s and 1 nano shake = 10^-9 s

Question 17

Which of the following unit is equivalent to watt?

1. Volt x Ampere
2. Volt/Ampere
3. Ampere/Volt
4. Ohm

Answer

Volt x Ampere

Reason — watt is the unit of electrical power and is defined as potential x current = volt x ampere.

Question 18

Which one of the following is a derived unit?

1. Metre
2. Kelvin
3. Metre³
4. Mole

Answer

Metre³

Reason — Volume is a derived unit. Its formula is:
Volume = length x breadth x height
= metre x metre x metre = metre³

Question 19

The S.I. unit of energy is:

1. Joule
2. Kg m²
3. Kg m²s^-3
4. Kg m²s^-1

Answer

Joule

Reason — Work done or energy = force x displacement = kgm²s^-2 or J

Question 20

The S.I. unit of pressure is:

1. Kg m^-2s^-2
2. Kg m^-1s^-2
3. Kg m²
4. Kg ms^-2

Answer

Kg m^-1s^-2

Reason — Pressure = $\dfrac{\text{force}}{\text{area}}$ = Kg m^-1s^-2

Question 21

Which of the following is the smallest unit?

1. Millimetre
2. Angstrom
3. Fermi
4. Metre

Answer

Fermi

Reason — Fermi is 10^-15th part of a metre. i.e., 1 fermi = 10^-15 m, hence it is the smallest unit.

Angstrom = 10^-10th part of a metre.
Millimetre = 10^-3th part of a metre.

Exercise 1(A) — Very Short Answer Type

Question 1

What is meant by measurement?

Answer

Measurement is the process of comparison of the given quantity with the known standard quantity of the same nature.

Question 2

What do you understand by the term unit?

Answer

Unit is the quantity of a constant magnitude which is used to measure the magnitudes of other quantities of the same nature.

Question 3

How is a physical quantity expressed?

Answer

A physical quantity is expressed in terms of the following parameters:

1. The unit in which the quantity is being measured, and
2. The numerical value which expresses, how many times the above selected unit is contained in the given quantity.

Thus, the magnitude of physical quantity is expressed as : Physical quantity = (numerical value) x (unit)

Question 4

Name the three fundamental quantities.

Answer

The three fundamental quantities are —

1. Mass
2. Length
3. Time

Question 5

What is the S.I. unit of Luminous intensity?

Answer

The S.I. unit of Luminous intensity is candela (cd).

Question 6

Define one parsec.

Answer

One parsec is the distance from where the semi major axis of orbit of earth (1 A.U.) subtends an angle of one second.

Question 7

Define a fundamental unit.

Answer

A fundamental unit is that which is independent of any other unit or which can neither be changed nor can be related to any other fundamental unit.

Example – Units of mass, length, time, temperature, current etc.

Question 8

Define a derived unit.

Answer

Derived units are those which depend on the fundamental units or which can be expressed in terms of fundamental units.

Example: For the measurement of area, we need to measure length and breadth in the unit of length and then express area in a unit which is length x length or (length)²

Question 9

Define standard metre.

Answer

The standard metre is defined in terms of speed of light, according to which, one metre is the distance travelled by light in 1/299,792,458 of a second in air (or vacuum).

Question 10

How is nanometer related to Angstrom ?

Answer

Relation between nanometer (nm) and Angstrom (Å) is expressed as:
    1 nanometer = 10 Å

Question 11

Complete the following —

1. 1 light year = ________ m
2. 1 m = ________ Å
3. 1 m = ________ µ
4. 1 micron = ________ Å
5. 1 fermi = ________ m

Answer

1. 1 light year = 9.46 x 10¹⁵ m
2. 1 m = 10¹⁰ Å
3. 1 m = 10⁶ µ
4. 1 micron = 10⁴ Å
5. 1 fermi = 10^-15 m

Question 12

Complete the following —

1. 1g = ______kg
2. 1mg = ________kg
3. 1 quintal = ________kg
4. 1 a.m.u (or u) = ________kg

Answer

1. 1 g = 10^-3 kg
2. 1 mg = 10^-6 kg
3. 1 quintal = 100 kg
4. 1 a.m.u (or u) = 1.66 x 10^-27 kg

Question 13

What is a leap year?

Answer

A leap year is the year in which the month of February is of 29 days.

1 Leap year = 366 days

Every fourth year (i.e., the year divisible by 4) has one day extra in the month of february (i.e., February has 29 days) and so it is the leap year.

Question 14

'The year 2024 will have February of 29 days'. Is this statement true?

Answer

Yes the statement is true.

We know that, if any year is divisible by 4, then it is a leap year and in a leap year, February has 29 days. As, the year 2024 is divisible by 4, so it will have 29 days in February.

Question 15

What is a lunar month?

Answer

A lunar month is the time of one lunar cycle, i.e., it is the amount of time it takes for the Moon to complete one orbit around the Earth and it is nearly equal to 29.5 days.

Question 16

Complete the following —

1. 1 nano second = ________s
2. 1 µs = _______s
3. 1 mean solar day = ________s
4. 1 year = ________s

Answer

1. 1 nano second = 10^-9 s
2. 1 µs = 10^-6 s
3. 1 mean solar day = 86400 s
4. 1 year = 3.15 x 10⁷ s

Question 17

Name the physical quantities which are measured in the following units —

1. u
2. ly
3. ns
4. nm

Answer

Physical quantity related to the unit are as follows —

Question 18

Write the derived units of the following —

1. Speed
2. Force
3. Work
4. Pressure

Answer

The derived units of the following quantities are as follows —

Question 19

How are the following derived units related to the fundamental units?

1. Newton
2. Watt
3. Joule
4. Pascal

Answer

Question 20

Name the physical quantities related to the following units —

1. km²
2. newton
3. joule
4. pascal
5. watt

Answer

The physical quantities related to the following units are —

Exercise 1(A) — Short Answer Type

Question 1

What are the three requirements for selecting a unit of a physical quantity?

Answer

The three requirements for selecting a unit of a physical quantity are —

1. The unit should be of convenient size.
2. It should be possible to define the unit without any ambiguity.
3. The unit should be reproducible.
4. The value of unit should not change with space and time. (i.e. it must always remain same everywhere).

Question 2

What are the fundamental units in S.I. system? Name them along with their symbols.

Answer

The fundamental units in S.I. system along with their symbols are as follows —

Question 3

Explain the meaning of derived unit with the help of one example.

Answer

The units of quantities other than those measured in fundamental units, can be expressed in terms of the fundamental units and they are called derived units.

Thus, derived units are those which depend on the fundamental units or which can be expressed in terms of the fundamental units.

Example – For the measurement of area, we need to measure length and breadth in the unit of length and then express area in a unit which is:

length x length or (length)².

Question 4

Name two units of length which are bigger than a metre. How are they related to the metre?

Answer

The units of length which are bigger than a metre are —

1. Astronomical Unit (A.U.) — One astronomical unit is equal to the mean distance between the earth and the sun. Relation between metre and astronomical unit is expressed as:
       A.U. = 1.496 x 10¹¹m
2. Light year (ly) — A light year is the distance travelled by light in vacuum, in one year. Relation between metre and light year is expressed as:
       1 light year = 9.46 x 10¹⁵m

Question 5

Name the three convenient units used to measure length ranging from very short to very long value. How are they related to the S.I. unit ?

Answer

The 3 convenient units used to measure length ranging from very short to very long value are —

1. Centimeter (cm)
2. Metre (m)
3. Kilometer (km)

S.I. unit of length is meter (m). Relation between meter (m) and centimeter is —

    1 m = 100cm

Relation between meter (m) and kilometer is —

    1 km = 1000m

Question 6

Name the S.I. unit of mass and define it.

Answer

The S.I. unit of mass is Kilogram (Kg).

One kilogram is defined as the mass of a cylindrical piece of platinum-iridium alloy kept at International Bureau of Weights and Measures at Serves near Paris.

Question 7

State two units of mass smaller than a kilogram. How are they related to kilogram ?

Answer

The two units of mass smaller than a kilogram (kg) are:

1. gram (g) — Relation between gram and kilogram is:
       1 g = 10^-3 kg
2. milligram (mg) — Relation between miligram and kilogram is:
       1 mg = 10^-6 kg

Question 8

State two units of mass bigger than a kilogram. Give their relationship with the kilogram.

Answer

The two units of mass bigger than a kilogram (kg) are:

1. Quintal — It is one hundred times a kilogram. Relation between quintal and kilogram is:
       1 quintal = 100 kg
2. Metric tonne — It is one thousand times a kilogram. Relation between metric tonne and kilogram is:
       1 metric tonne = 1000 kg

Question 9

Name the S.I. unit of time and define it.

Answer

The S.I. unit of time is second (s).

A second can be defined as 1/86400th part of a mean solar day,

i.e.,

$1s = \dfrac{1}{86400} \times \text{one mean solar day}$

Question 10

Name two units of time bigger than a second. How are they related to second?

Answer

The two units of time bigger than a second (s) are:

1. Minute (min) — One minute is the duration of 60 seconds. Relation between minute and second is:
       1 min = 60s
2. Hour (h) — One hour is the duration of 60m minutes. Relation between hour and second is:
       1 h = 3600s

Exercise 1(A) — Numericals

Question 1

The wavelength of light of a particular colour is 5800 Å.

Express it in —

(a) nanometer and

(b) metre

Answer

As we know, 1nm = 10 Å

Given,

The wavelength of light = 5800 Å

Substituting the value of wavelength in the relation above, we get,

$10 Å = 1nm \\[0.5em] 1 Å = \dfrac{1}{10}nm \\[0.5em] 5800 Å = \dfrac{1}{10} \times 5800 nm\\[0.5em] \Rightarrow 5800 Å = 580 nm\\[0.5em]$

Hence, wavelength of 5800 Å in nm = 580 nm.

(b) As we know,
1m = 10¹⁰ Å

Given,

The wavelength of light = 5800 Å

Substituting the value of wavelength in the relation above, we get,

$10^{10} Å = 1m \\[0.5em] 1 Å = 10^{-10} m \\[0.5em] 5800 Å = 5800 \times 10^{-10} m \\[0.5em] \Rightarrow 5800 Å = 5.8 \times 10^{-7} m \\[0.5em]$

Hence, wavelength of 5800 Å in m = 5.8 x 10 ^-7m.

Question 2

The size of a bacteria is 1 µ. Find the number of bacteria in 1m length.

Answer

Given,

Size of a bacteria = 1 µ

Total length = 1m

∴ Number of bacteria in 1m length = $\dfrac{1 m}{ 1 µ}$

As we know, 1 µ = 10^-6m, substituting the value in the relation above we get:

Number of bacteria in 1m length = $\dfrac{1 m}{10^{-6}m}$

Hence,
number of bacteria in 1m length = 10⁶ bacteria.

Question 3

The distance of a galaxy from the earth is 5.6 x 10²⁵m. Assuming the speed of light to be 3 x 10⁸ ms-1, find the time taken by light to travel this distance.

Hint —

$\text{Time taken} =\dfrac{\text{distance travelled}}{\text{speed}}$

Answer

Given,

$\text{Time taken} =\dfrac{\text{distance travelled}}{\text{speed}}$

distance = 5.6 x 10²⁵m

speed = 3 x 10⁸ ms^-1

Substituting the values in the formula above we get,

$\text{Time taken} =\dfrac{5.6 \times 10^{25}}{3 \times 10^8} \\[0.5em] \Rightarrow \text{Time taken} ={1.87 \times 10^{17}} s \\[0.5em]$

∴, time taken by light = 1.87 x 10¹⁷s.

Question 4

The wavelength of light is 589nm. What is its wavelength in Å?

Answer

As we know, 1nm = 10 Å

Given,

The wavelength of light = 589nm

Substituting the value of wavelength in the relation above, we get,

$1nm = 10 Å \\[0.5em] 589nm = 589 \times 10 Å \\[0.5em] \Rightarrow 589nm = 5890 Å \\[0.5em]$

Hence, the wavelength of light in Å is 5890 Å.

Question 5

The distance of the nearest star, Proxima Centauri, from the Earth is 4.0 x 10¹³ km. Express it in light year.

Answer

1 Light year = 9.46 x 10¹² km

or 9.46 x 10¹² km = 1 Light year

∴ 4.0 x 10¹³ km

= $\dfrac{1}{9.46 \times 10^{12}}$ x 4.0 x 10¹³

= 4.2 light years.

Hence, distance of the nearest star from earth = 4.2 light years.

Question 6

It takes time 8 min for light to reach from the sun to the earth surface. If speed of light is taken to be 3 x 10⁸ms^-1, find the distance from the sun to the earth in km.

Answer

As we know, Distance = speed x time

Given,

Speed = 3 x 10⁸ms^-1

Time = 8 min = 8 x 60s = 480s

Substituting the values in the formula above we get,

Distance = 3 x 10⁸ x 480 = 1440 x 10⁸ m.

Converting the distance to km:

Distance in km = $\dfrac{1440 \times 10^8}{1000}$ km
= 1.44 x 10⁸ km

∴,
the distance from the sun to the earth is 1.44 x 10⁸ km.

Question 7

'The distance of a star from the earth is 8.33 light minutes'. What do you mean by this statement? Express the distance in metre.

Answer

'The distance of a star from the earth is 8.33 light minutes' implies, it takes 8.33 minutes for light to reach the earth from the star.

As we know,
Distance = speed x time

Given,

Speed = 3 x 10⁸ms^-1

Time = 8.33 min
= 8.33 x 60s
= 499.8s
≈ 500s

Substituting the values in the formula above we get,

Distance = 3 x 10⁸ x 500
= 1500 x 10⁸
= 1.5 x 10¹¹

∴, the distance from the star to the earth is 1.5 x 10¹¹ m.

Exercise 1(B) — Multiple Choice Type

Question 1

Least count of metre rule having 10 subdivisions in 1 cm is:

1. 0.01 mm
2. 1 mm
3. 0.001 mm
4. 1 cm

Answer

1 mm

Reason — The least count of a metre rule is the value of its one division which is one-tenth of a centimetre (or 1 mm).

Question 2

The least count of a vernier callipers is:

1. 1 cm
2. 0.001 cm
3. 0.1 cm
4. 0.01 cm

Answer

0.01 cm

Reason — Least count of a vernier callipers is given by the formula:

$\text{Least count (L.C.)} = \dfrac{\text{ Value of 1 main scale div (x)}}{\text {total no. of div on vernier(n)}}$

Hence, least count of a vernier callipers whose main scale is graduated to read 1 mm and vernier scale has 10 division will be:

$\text{Least count (L.C.)} = \dfrac{1\text{ mm}}{10} \\[0.5em] \text{Least count (L.C.)} = 0.1\text{ mm} = 0.01\text{ cm} \\[0.5em]$

Question 3

The strip of a vernier callipers is used to measure:

1. Length of a wire
2. Depth of a beaker
3. Internal diameter of a sphere
4. Diameter of a hollow sphere

Answer

Depth of a beaker

Reason — The function of Vernier callipers' strip is to measure the depth of a beaker.

Question 4

On bringing the two jaws of a vernier callipers together, the 6th division of vernier scale coincides with the main scale. If the least count of the vernier callipers is 0.01 cm, then its zero error is:

1. +0.06 cm
2. +0.6 cm
3. +0.006 cm
4. +0.001 cm

Answer

+0.06 cm

Reason — Zero error = +6 x Least count = +6 x 0.01 = 0.06 cm

Question 5

A microscope has its main scale with 20 divisions in 1 cm and vernier scale with 25 divisions, the length of which is equal to the length of 24 divisions of main scale. The least count of microscope is :

1. 0.002 cm
2. 0.001 cm
3. 0.02 cm
4. 0.01 cm

Answer

0.002 cm

Reason — The value of one main scale division x = $\dfrac{1}{20}$ cm

The number of divisions on vernier scale n = 25

Using the formula given below,

$\text{Least count (L.C.)} = \dfrac{\text{ Value of 1 main scale div (x)}}{\text {total no. of div on vernier(n)}}$

we get,

$\text {L.C.} = \dfrac{\text{x}}{\text{n}} \\[0.5em] \text{L.C.} = \dfrac{\dfrac{\text{1}}{\text{20}}}{25}\text{ cm} \\[0.5em] \text{L.C.} = \dfrac{\text{1}}{\text{500}}\text{ cm} \\[0.5em] \Rightarrow \text{L.C.} = 0.002\text{ cm} \\[0.5em]$

Hence, least count of microscope is 0.002 cm.

Question 6

Identify the correct use of the thimble of a screw gauge:

1. To read length correct up to 0.01 mm
2. To read length correct up to 1 mm
3. To mark main scale and base line
4. To mark circular scale.

Answer

To mark circular scale.

Reason — Use of the thimble of a screw gauge is to mark the circular scale.

Question 7

Ratchet is a part of:

1. Vernier callipers
2. Slide callipers
3. Screw gauge
4. None of these

Answer

Screw gauge

Reason — Ratchet is a part of screw gauge used to advance the screw by turning it till the object is gently held between the stud and spindle of the screw.

Question 8

The diameter of a thin wire can be measured by —

1. A vernier callipers
2. A metre rule
3. A screw gauge
4. None of these

Answer

A screw gauge

Reason — A screw gauge is used to measure the diameter of a thin wire.

Question 9

The circular head of a screw gauge is divided into 50 divisions and the screw moves 1 mm ahead in two revolutions of the circular head. Its pitch would be:

1. 0.05 cm
2. 0.001 cm
3. 0.5 cm
4. 0.01 cm

Answer

0.05 cm

Reason — Pitch = distance moved ahead in 1 revolution

Given, distance moved in 2 revolutions = 1 mm

∴ Distance moved in 1 revolution = $\dfrac{1}{2}$ mm = 0.5 mm

Converting 0.5 mm to cm,

0.5 mm = $\dfrac{0.5}{10}$ cm = 0.05 cm

∴ Pitch of screw gauge is 0.05 cm

Question 10

Which of the following is the correct ascending order of accuracy?

1. Metre rule, vernier callipers, screw gauge
2. Vernier callipers, metre rule, screw gauge
3. Screw gauge, vernier callipers, metre rule
4. None of the above.

Answer

Metre rule, vernier callipers, screw gauge

Reason — The least count of each is :

Meter rule = 0.1 cm
Vernier callipers = 0.01 cm
Screw gauge = 0.001 cm

Hence, the ascending order of accuracy is as follows:

Metre rule, vernier callipers, screw gauge

Exercise 1(B) — Very Short Answer Type

Question 1

Define the least count of an instrument.

Answer

Least count of an instrument is the smallest measurement that can be taken accurately with it.

Question 2

How can you decrease the least count of a vernier callipers?

Answer

The least count of a vernier callipers can be decreased by:

1. increasing the number of divisions on the vernier scale.
2. decreasing the value of one division on main scale.

Question 3

Define the term 'Vernier constant'?

Answer

The term 'Vernier constant' is defined as the difference between the values of one main scale division and one vernier scale division. It is also known as least count of vernier.

Question 4

When is a vernier callipers said to be free from zero error?

Answer

On bringing, the movable jaw in contact with the fixed jaw, the zero mark of the vernier scale should coincide with the zero mark of the main scale. In this position, the tenth division of the vernier callipers coincides with the ninth division of the main scale.

If it is so, the vernier is said to be free from zero error.

Question 5

Name the part of the vernier callipers which is used to measure the following —

1. external diameter of a tube,
2. internal diameter of a mug,
3. depth of a small bottle,
4. thickness of a pencil.

Answer

1. External diameter of a tube — Outside jaws
2. Internal diameter of a mug — Inside jaws
3. Depth of a small bottle — Strip
4. Thickness of a pencil — Outer jaws

Question 6

State the difference between positive and negative zero error of a vernier callipers.

Answer

On bringing the two jaws of a vernier callipers together, if zero mark of the vernier scale is on the right of zero mark of the main scale, the zero error is said to be positive and if zero mark of the vernier scale is to the left of zero mark of the main scale, the zero error is said to be negative.

Question 7

Define the pitch of a screw gauge.

Answer

The pitch of a screw gauge is the linear distance moved by its screw on the main scale when the circular scale is given one complete rotation.

Question 8

State one use of a screw gauge.

Answer

A screw gauge is used to measure the diameter of a wire or thickness of a paper, etc.

Question 9

State the purpose of ratchet in a screw gauge.

Answer

The purpose of a ratchet in a screw gauge is to advance the screw by turning it till the object is gently held between the stud and the spindle of the screw.

Question 10

State the difference between positive and negative zero error of a screw gauge.

Answer

If on bringing the flat end of the screw in contact with the stud, the zero mark on the circular scale is below the base line of the main scale, the zero error is said to be positive and if the zero mark on the circular scale is above the base line of the main scale, the zero error is said to be negative.

Question 11

Name the instrument which can measure accurately the following —

1. the diameter of a needle,
2. the thickness of a paper,
3. the internal diameter of the neck of a water bottle,
4. the diameter of a pencil.

Answer

The given physical quantities can be measured accurately with the help of the following instruments —

1. the diameter of a needle — screw gauge.
2. the thickness of a paper — screw gauge.
3. the internal diameter of the neck of a water bottle — vernier callipers.
4. the diameter of a pencil — screw gauge.

Question 12

Which of the following measures a small length to a high accuracy — metre rule, vernier callipers, screw gauge?

Answer

A screw gauge measures a small length to a high accuracy.

Question 13

Name the instrument which has the least count —

1. 0.1 mm
2. 1 mm
3. 0.01 mm

Answer

The following instruments have the given least count —

1. 0.1 mm — vernier callipers
2. 1 mm — metre rule
3. 0.01 mm — screw gauge

Exercise 1(B) — Short Answer Type

Question 1

Explain the meaning of the term ‘least count of an instrument’ by taking a suitable example.

Answer

The least count of an instrument is the smallest measurement that can be taken accurately with it.

Example — The least count of a stop watch is 0.5 second, if there are 10 divisions between 0 and 5s marks.

Question 2

A boy makes a ruler with graduation in cm on it (i.e., 100 divisions in 1 m). To what accuracy this ruler can measure ? How can this accuracy be increased ?

Answer

The ruler graduated by the boy, was having its zero mark at one end and 100 cm mark at the other end.

It had 100 subdivisions in one metre length, so the value of its one small division is 1 cm.

Thus, the ruler can be used to measure length accurately up to 1 cm.

In order to increase the accuracy, each cm should be further divided into 10 divisions so that the ruler can have a least count of 1 mm.

Question 3

A boy measures the length of a pencil and expresses it to be 2.6cm. What is the accuracy of his measurement? Can he write it as 2.60cm?

Answer

Given, the length of the pencil is 2.6 cm.

As the length is measured in cm till one place of decimal, we can assume that it was measured using a metre rule.

So, the measurement is accurate

No, it cannot be written as 2.60, as it would mean that length is measured precisely up to second decimal place using vernier callipers or a screw gauge.

Question 4

Define least count of a vernier callipers. How do you determine it?

Answer

The least count of a vernier callipers is equal to the difference between the values of one main scale division and one vernier scale division.

It is calculated as below —

$\text{Least count (L.C.)} = \text{ Value of 1 main scale div} - \text{Value of 1 vernier scale div}$

Question 5

A vernier callipers has a zero error +0.06cm. Draw a neat labelled diagram to represent it.

Answer

Below diagram shows a vernier callipers with a zero error of +0.06 cm.

The least count of the vernier callipers shown in the diagram is 0.01 cm and the 6^th division of the vernier scale, coincides with a main scale division.

∴,

$\text{Zero Error} = 6 \times \text{L.C.} \\[0.5em] \text{Zero Error}= 6 \times 0.01 \text{cm} \\[0.5em] \Rightarrow \text{Zero Error}= 0.06 \text {cm} \\[0.5em]$

Hence, we get the zero error = 0.06 cm.

Question 6

State three uses of a vernier callipers.

Answer

Three uses of vernier callipers are as follows —

1. It is used to measure the length of a rod.

2. It is used to measure the diameter of a sphere.

3. It is used to measure the internal and external diameter of a hollow cylinder.

Question 7

Name the two scales of a vernier callipers and explain, how it is used to measure a length correct up to 0.01 cm.

Answer

The two scales of a vernier callipers are —

1. Main scale - it is fixed
2. Vernier scale – slides along the main scale.

In the figure shown above, the main scale is graduated to read up to 1mm and the vernier scale has the length of 10 divisions equal to the length of 9 divisions of main scale.

Value of 1 division of main scale (x) = 1mm.

Total number of divisions on the vernier scale (n) = 10

Using the formula given below,

$\text{Least count (L.C.)} = \dfrac{\text{ Value of 1 main scale div (x)}}{\text {total no. of div on vernier (n)}}$

Substituting the value in the formula above, we get,

$\text{Least count (L.C.)} = \dfrac{\text{x}}{\text{n}} \\[0.5em] \text{Least count (L.C.)} = \dfrac{\text{1}}{\text{10}} \text{mm} \\[0.5em] \text{Least count (L.C.)} = 0.1\text{mm} \\[0.5em] \Rightarrow \text{Least count (L.C.)} = 0.01\text{cm} \\[0.5em]$

Hence, a vernier callipers is used to measure a length accurately up to 0.01cm.

Question 8

Explain the terms —

(i) pitch, and

(ii) least count of a screw gauge.

How are they determined?

Answer

1. Pitch of a screw gauge — The pitch of a screw gauge is the linear distance moved by its screw on the main scale when the circular scale is given one complete rotation.

2. Least count of a screw gauge — Least count of a screw gauge is the linear distance moved by its screw along the main scale when the circular scale is rotated by one division on it.

The pitch and least count of the screw gauge are determined by using the formula —

$\text{Least Count} = \dfrac{\text{Pitch of screw gauge}}{\text{Total no. of div on circular scale}}$

Question 9

How can the least count of a screw gauge be decreased?

Answer

The least count can be decreased by —

1. Decreasing the pitch.

2. Increasing the total number of divisions on the circular scale.

Question 10

What do you mean by zero error of a screw gauge? How is it accounted for?

Answer

In an ideal case, when the flat end B of the screw is in contact with the stud A, and if the zero mark of circular scale coincide with the base line of main scale, the screw gauge is said to be free from zero error.

But sometimes, due to the mechanical error, on bringing the stud A in contact with stud B, the zero mark of the circular scale is either below or above the base line of the main scale, then the screw gauge is said to have a zero error.

There are two types of zero error —

1. Positive zero error and

2. Negative zero error.

The zero error is accounted by subtracting the zero error with its sign from the observed reading.

Correct reading = Observed reading - Zero error (with sign)

Question 11

A screw gauge has a least count 0.001 cm and zero error + 0.007 cm. Draw a neat diagram to represent it.

Answer

Below diagram shows a screw gauge with least count 0.001 cm and zero error + 0.007 cm:

Question 12

What is backlash error? Why is it caused? How is it avoided?

Answer

Sometimes, it is observed that on reversing the direction of rotation of the thimble, the tip of the screw does not start moving in the opposite direction at once, but it remains stationary for a part of rotation. This causes error in the observation which is called backlash error.

The reason for this is the wear and tear of threads of screw.

To avoid the error, while taking the measurements, screw should be rotated in one direction only.

If it is required to change the direction of rotation of screw then do not change the direction of rotation at once. Move the screw still further, stop there for a while and then rotate it in the reverse direction.

Exercise 1(B) — Long Answer Type

Question 1

What is meant by zero error of a vernier callipers? How is it determined? Draw neat diagrams to explain it. How is it taken in account to get the correct measurement?

Answer

Sometimes due to mechanical error in vernier callipers, the zero mark of the vernier scale does not coincide with the zero mark on the main scale. Hence, the vernier callipers is said to have a zero error.

In order to find the zero error, we note the division of the vernier scale which coincides with any division of the main scale. The number of this vernier division when multiplied by the least count of the vernier gives the zero error.

For example if the least count is 0.01 cm and the 6th division of the vernier scale, coincides with a main scale division then.

we get,

$\text{Zero Error} = 6 \times \text{L.C.} \\[0.5em] \text{Zero Error}= 6 \times 0.01 \text{cm} \\[0.5em] \Rightarrow \text{Zero Error}= 0.06 \text {cm} \\[0.5em]$

Hence, zero error = 0.06 cm.

In order to correct the measurement of the vernier callipers with zero error, the zero error with proper sign is subtracted from the observed reading.

Hence, Correct reading = observed reading – zero error (with sign)

Question 2

Draw a neat labelled diagram of a vernier callipers. Name its main parts and state their functions.

Answer

A neat labelled diagram of a vernier callipers is shown below:

The main parts of the vernier callipers are as follows —

Question 3

Describe in steps, how would you use a vernier callipers to measure the length of a small rod?

Answer

In order to measure the length of a small rod, we follow the following steps:

1. Find the least count and zero error of the vernier callipers.

2. The rod is placed between the fixed end and the vernier scale as shown in the diagram.

3. Note the main scale reading.

4. Note that division p on vernier scale which coincide or is in line with any division of the main scale. Multiply this vernier division p with the least count. This is the vernier scale reading i.e., Vernier scale reading = p x L.C.

5. Repeat it two times and record the observation.

Observations —

Total number of divisions on vernier scale (n) = ...........

Value of one division on main scale (x) = ........... cm

$\text {Least count (L.C.)} = \dfrac{\text{x}}{\text{n}} = ..........\text{cm}$

Zero error = ....... cm

Mean observed length = ......... cm

From the mean observed length, subtract zero error, if any, with its proper sign to obtain the true measurement of the length of the given project.

Thus we get,

Observed length = main scale reading + (vernier division p coinciding with any division on the main scale) x least count.

True length = observed length - zero error (with sign).

Question 4

Draw a neat and labelled diagram of a screw gauge. Name its main parts and state their functions.

Answer

Below is the diagram of a screw gauge with all its parts labelled:

The main parts and their functions of a screw gauge are as follows —

Question 5

Describe the procedure to measure the diameter of a wire with the help of a screw gauge.

Answer

In order to measure the diameter of a wire with the help of a screw gauge we follow the following steps —

1. Find the least count and the zero error of the screw gauge.

2. Turn the ratchet anticlockwise, so as to obtain a gap between the stud A and the flat end B. Place the wire in the gap between the stud A and the flat end B. Then turn the ratchet clockwise so as to hold the given wire gently between the stud A and the flat end B of the screw.

3. Note the main scale reading.

4. Note that division p of the circular scale that coincides with the base line of the main scale. This circular scale division p when multiplied by the least count, gives the circular scale reading i.e., Circular scale reading = p x L.C.

5. Add the circular scale reading to the main scale reading to obtain the total reading (i.e., the observed diameter of the wire).

6. Repeat it by keeping the wire in perpendicular direction. Take two more observations at different places of the wire and record them in a table.

Observations —

Pitch of the screw = ......... cm

Total number of divisions on the circular scale (n) = ...........

$\text {L.C. of screw gauge} = \dfrac{\text{Pitch}}{\text{Total no. of circular scale div}} = ..........\text{cm}$

Zero error = ....... cm

Mean observed length = ......... cm

From the mean observed length, subtract zero error, if any, with its proper sign to obtain the true measurement of the length of the given project.

Thus we get,

Thus,

Observed diameter = main scale reading + (circular scale division p coinciding the coinciding the base line of main scale x least count).

True diameter = observed diameter - zero error (with sign)

Exercise 1(B) — Numericals

Question 1

A stop watch has 10 divisions graduated between the 0 and 5s marks. What is its least count?

Answer

Using the formula given below,

$\text{Least count (L.C.)} = \dfrac{\text{ Value of one div (x)}}{\text {Total no. of div on stop watch (n)}}$

Given,

Total number of divisions on stop watch = 10

we get,

$\text{L.C.} = \dfrac{\text{x}}{\text{n}} \\[0.5em] \text{L.C.} = \dfrac{5}{10} \\[0.5em] \text{L.C.} = \dfrac{1}{2} \\[0.5em] \Rightarrow \text{L.C.} = 0.5\text{s}$

Hence, least count of stop watch is 0.5s.

Question 2

A vernier has 10 divisions and they are equal to 9 divisions of main scale in length. If the main scale is calibrated in mm, what is its least count?

Answer

(i) As we know,

$\text{L.C.} = \dfrac{\text{Value of 1 main scale div (x)}}{\text{Total no. of div on vernier (n)}}$

Given,

Total number of divisions on vernier = 10

Value of one main scale division(x) = 1 mm

Substituting the values in the formula given above we get,

$\text{L.C.} = \dfrac{\text{1mm}}{\text{10}} \\[0.5em] \Rightarrow \text{L.C.} = 0.1 \text{mm} \\[0.5em] \Rightarrow \text{L.C.} = 0.01 \text{cm} \\[0.5em]$

Hence, least count of the vernier callipers is 0.01cm.

Question 3

A microscope is provided with a main scale graduated with 20 divisions in 1cm and a vernier scale with 50 divisions on it of length same as of 49 divisions of main scale. Find the least count of the microscope.

Answer

i) As we know,

$\text{L.C.} = \dfrac{\text{Value of 1 main scale div (x)}}{\text{Total no. of div on vernier(n)}}$

Given,

20 divisions = 1 cm

∴,

$\text{1 division} = \dfrac{1}{20} \\[0.5em] \Rightarrow \text{1 division} = 0.05 \text{cm}$

Hence, value of one main scale division = 0.05 cm

Total number of divisions = 50

Substituting the values in the formula above, we get,

$\text{L.C.} = \dfrac{\text{0.05} \text{cm}}{\text{50}} \\[0.5em] \text{L.C.} = 0.001 \text{cm} \\[0.5em]$

Hence, least count of the microscope is 0.001 cm.

Question 4

A boy uses a vernier callipers to measure the thickness of his pencil. He measures it to be 1.4mm. If the zero error of vernier callipers is +0.02cm, what is the correct thickness of pencil?

Answer

As we know,

Correct reading = observed reading – zero error (with sign)

Given,

Thickness of the pencil = 1.4 mm

Zero error of the vernier callipers = +0.02cm = 0.2 mm

Substituting the values in the formula above we get,

Correct reading = observed reading - zero error (with sign)
Correct reading = 1.4mm - 0.2mm
Correct reading = 1.2mm

Hence, correct thickness of pencil is 1.2 mm

Question 5

A vernier callipers has its main scale graduated in mm and 10 divisions on its vernier scale are equal in length to 9 mm. When the two jaws are in contact, the zero of vernier scale is ahead of zero of main scale and 3rd division of vernier scale coincides with a main scale division.

Find —

(i) the least count and

(ii) the zero error of the vernier callipers.

Answer

(i) As we know,

$\text{L.C.} = \dfrac{\text{Value of 1 main scale div (x)}}{\text{Total no. of div on vernier(n)}}$

Given,

Total number of divisions on vernier (n) = 10

Value of one main scale division (x) = 1 mm

Substituting the values in the formula above, we get,

$\text{L.C.} = \dfrac{\text{1mm}}{\text{10}} \\[0.5em] \text{L.C.} = 0.1 \text{mm} \\[0.5em] \text{L.C.} = 0.01 \text{cm} \\[0.5em]$

Hence, least count of the vernier callipers is 0.01cm.

(ii) As we know,

Zero error = L.C. x Coinciding division (with sign)

and

Coinciding division = 3

L.C. = 0.01 cm

Substituting the values in the formula above we get,

$\text {Zero error} = \text {0.01 cm x 3} \\[0.5em] \Rightarrow \text {Zero error} = \text {0.03 cm} \\[0.5em]$

Hence, the zero error of the vernier callipers = + 0.03 cm.

Question 6

The main scale of a vernier callipers is calibrated in mm and 19 divisions of main scale are equal in length to 20 divisions of vernier scale. In measuring the diameter of a cylinder by this instrument, the main scale reads 35 divisions and 4th division of vernier scale coincides with a main scale division.

Find —

(i) least count and

(ii) radius of cylinder.

Answer

(i) As we know,

$\text{Least count (L.C.)} = \dfrac{\text{ Value of 1 main scale div (x)}}{\text{total no. of div on vernier (n)}}$

Given,

Value of one main scale division(x) = 1 mm

Total number of divisions on vernier callipers (n) = 20

Substituting the values in the formula above we get,

$\text{L.C.} = \dfrac{1}{\text{20}} \\[0.5em] \text{L.C.} = 0.05 \text{mm} \\[0.5em] \text{L.C.} = 0.005 \text{cm} \\[0.5em]$

Hence, least count of the vernier callipers is 0.005 cm.

(ii) As we know,

circular scale reading = L.C. x Coinciding division

Given,

Coinciding division = 4

L.C. = 0.005 cm

Substituting the values in the formula above we get,

$\text {circular scale reading} = \text {0.005 cm x 4} \\[0.5em] \Rightarrow \text {circular scale reading} = \text {0.02 cm} \\[0.5em]$

Hence, the circular scale reading = 0.02 cm. ...... (1)

Main scale reading = 3.5 cm (as it reads 35th division on mm scale)

Hence, the main scale reading = 3.5 cm. ........ (2)

Substituting the values 1 and 2 in the formula for total reading we get,

$\text{Total reading} = \text{main scale reading } + \text{ vernier scale reading} \\[0.5em] \text{Diameter = Total reading} = \text{3.5 cm + 0.02 cm} \\[0.5em] \Rightarrow \text{Diameter} = \text{3.52 cm} \\[0.5em] \Rightarrow \text{Radius} = \dfrac{3.52}{2}\text{cm} \\[0.5em] \Rightarrow \text{Radius} = 1.76\text{cm} \\[0.5em]$

Hence, the radius of the cylinder = 1.76 cm.

Question 7

In a vernier callipers, there are 10 divisions on the vernier scale and 1 cm on the main scale is divided in 10 parts. While measuring a length, the zero of the vernier lies just ahead of 1.8 cm mark and 4th division of vernier coincides with a main scale division.

1. Find the length

2. If zero of vernier callipers is -0.02cm, what is the correct length?

Answer

(i) As we know,

$\text{Least count (L.C.)} = \dfrac{\text{ Value of 1 main scale div (x)}}{\text{total no. of div on vernier (n)}}$

Given,

Total number of divisions on the vernier scale (n) = 10

Value of one main scale division (x) = 1 mm

Coinciding division = 4

Substituting the values in the formula above we get,

$\text{L.C.} = \dfrac{1}{\text{10}} \\[0.5em] \Rightarrow \text{L.C.} = 0.1\text{mm} \\[0.5em] \Rightarrow \text{L.C.} = 0.01\text{cm} \\[0.5em]$

Hence, least count of the vernier callipers is 0.01 cm.

As we know,

$\text{Vernier scale reading} = \text{Vernier scale division} \times \text{L.C.} \\[0.5em] \text{Vernier scale reading} = 4 \times 0.01 \text{cm} \\[0.5em] \Rightarrow \text{Vernier scale reading} = 0.04 \text{cm} \\[0.5em]$

Hence, Vernier scale reading is 0.04 cm.

and

Main scale reading of the vernier callipers = 1.8 cm

∴,

$\text{Total reading} = \text{main scale reading} + \text{vernier scale reading} \\[0.5em] \text{Total reading} = 1.8 \text{cm} + 0.04 \text{cm} \\[0.5em] \Rightarrow \text{Total reading}= 1.84\text{cm} \\[0.5em]$

Hence, the length is 1.84 cm.

(b) As we know,

$\text{Correct reading} = \text {observed reading} – \text{zero error}$

Given,

zero error is -0.02cm,

Substituting the values in the formula above we get,

$\text{Correct reading} = 1.84 – (-0.02) \\[0.5em] \text{Correct reading} = 1.84 + 0.02 \\[0.5em] \text{Correct reading} = 1.86 \text{cm} \\[0.5em]$

Hence, the correct length is 1.86 cm.

Question 8

While measuring the length of a rod with a vernier callipers, figure below shows the position of its scales. What is the length of the rod?

Answer

As we know,

$\text{Least count (L.C.)} = \dfrac{\text{ Value of 1 main scale div (x)}}{\text{total no. of div on vernier (n)}}$

There are 10 divisions on 1 cm on the main scale

∴,

$\text{Value of 1 main scale division(x)} = \dfrac{1}{10}\text{ cm} = 0.1 \text{cm} \\[0.5em]$

Total number of divisions on the vernier scale (n) = 10

$\text{Least count (L.C.)} = \dfrac{0.1}{10} \\[0.5em] \text{L.C.} = 0.01 \text {cm}\\[0.5em]$

Hence, the least count = 0.01 cm.

Given,

Main scale reading = 3.3 cm

coinciding division = 6

As we know,

$\text{Vernier scale reading} = \text{Vernier scale division} \times \text{L.C.} \\[0.5em] \text{Vernier scale reading} = 6 \times 0.01 \text{cm} \\[0.5em] \Rightarrow \text{Vernier scale reading} = 0.06 \text{cm} \\[0.5em]$

Hence, Vernier scale reading is 0.06 cm.

$\text{Observed reading} = \text{main scale reading} + \text{vernier scale reading} \\[0.5em] \text{Observed reading} = 3.3 \text{cm} + 0.06 \text{cm} \\[0.5em] \Rightarrow \text{Observed reading} = 3.36\text{cm} \\[0.5em]$

Hence, the length of the rod is 3.36 cm.

Question 9

The pitch of a screw gauge is 0.5 mm and the head scale is divided in 100 parts. What is the least count of screw gauge ?

Answer

As we know,

$\text {Least Count} = \dfrac{\text{Pitch}}{\text {Total no. of div on circular head}} \\[0.5em]$

Given,

Pitch = 0.5 mm

Number of divisions on circular head = 100

Substituting the values in the formula above we get,

$\text {Least count} = \dfrac{0.5}{100} \\[0.5em] \text {Least count} = 0.005 \text { mm} = 0.0005 \text { cm} \\[0.5em]$

Hence, the least count of the screw gauge = 0.005 mm or 0.0005 cm.

Question 10

The thimble of a screw gauge has 50 divisions. The spindle advances 1 mm when the screw is turned through two revolutions.

(i) What is the pitch of the screw gauge?

(ii) What is the least count of the screw gauge?

Answer

(i) As we know,

Pitch = distance moved ahead in 1 revolution

Given,

Distance covered in two revolutions = 1 mm

∴, we get,

$\text {Pitch} = \dfrac{1}{2} \text{ mm} = 0.5 \text{ mm} \\[0.5em]$

Hence, pitch of the screw gauge = 0.5 mm

(ii) As we know,

$\text{Least Count} = \dfrac {\text{Pitch}}{\text{Total no. of div on circular head}}\\[0.5em]$

Given,

Pitch = 0.5 mm

Total number of divisions on circular scale = 50

Substituting the values in the formula above we get,

$\text {Least count} = \dfrac{0.5}{50} \\[0.5em] \text {Least count} = 0.01 \text { mm} \\[0.5em]$

Hence, the least count of the screw gauge = 0.01 mm

Question 11

The pitch of a screw gauge is 1 mm and its circular scale has 100 divisions. In measurement of the diameter of a wire, the main scale reads 2 mm and 45th mark on circular scale coincides with the base line.

Find —

1. The least count, and
2. The diameter of the wire

Answer

(i) As we know,

$\text{Least Count} = \dfrac {\text{Pitch}}{\text{Total no. of div on circular head}}\\[0.5em]$

Given,

Pitch = 1 mm

Number of divisions on circular head = 100

Substituting the values in the formula above we get,

$\text {Least count} = \dfrac{1}{100} \text{mm} \\[0.5em] \text {Least count} = 0.01 \text {mm} = 0.001 \text {cm}\\[0.5em]$

Hence, the least count of the screw gauge = 0.001 cm

(ii) As we know,

Diameter of the wire = main scale reading + circular scale reading     [Equation 1]

and

Circular scale reading = p x L.C.     [Equation 2]

p = 45

L.C. = 0.001 cm

Substituting the values in the Equation 2 we get,

Circular scale reading = 45 x 0.001 = 0.045

Hence, circular scale reading = 0.045 cm

Given, main scale reads 2 mm = 0.2 cm

Hence, main scale reading = 0.2 cm

Substituting the values in Equation 1 we get,

Diameter of the wire = 0.2 cm + 0.045 cm = 0.245 cm

Hence, the diameter of the wire is 0.245 cm.

Question 12

When a screw gauge of least count 0.01 mm is used to measure the diameter of a wire, the reading on the sleeve is found to be 1 mm and the reading on the thimble is found to be 27 divisions.

1. What is the diameter of the wire in cm?

2. If the zero error is +0.005 cm, what is the correct diameter?

Answer

As we know,

Diameter of the wire = main scale reading + circular scale reading     [Equation 1]

and

Reading on thimble = p x L.C.     [Equation 2]

Given,

p = 27

L.C. = 0.01 mm = 0.001 cm

Substituting the values in the Equation 2 we get,

reading on thimble = 27 x 0.001 = 0.027 cm

Hence, reading on thimble = 0.027 cm and reading on sleeve = 1 mm = 0.1 cm

Using Equation 1 we get,

Diameter of the wire = 0.1 cm + 0.027 cm = 0.127 cm

Hence, the diameter of the wire is 0.127 cm.

(ii) As we know,

Correct reading = observed reading - zero error

Given,

Zero error = + 0.005 cm

Substituting the value of zero error in the formula above we get,

Correct reading = 0.127 cm - 0.005 cm = 0.122 cm

Hence, the correct diameter of the wire is 0.122 cm

Question 13

A screw gauge has 50 divisions on its circular scale and its screw moves by 1 mm on turning it by two rotations. When the flat end of the screw is in contact with the stud, the zero of circular scale lies below the base line and 4th division of circular scale is in line with the base line.

Find —

(i) the pitch,

(ii) the least count and

(iii) the zero error, of the screw gauge.

Answer

As we know,

Pitch = Distance moved ahead in 1 revolution.

Given,

Total number of divisions on circular scale = 50

Distance covered in two revolutions = 1 mm

∴, we get,

$\text {Pitch} = \dfrac{1}{2} \text{ mm} = 0.5 \text{ mm} \\[0.5em]$

Hence, pitch of the screw gauge = 0.5 mm

(ii) As we know,

$\text{Least count} = \dfrac {\text{Pitch}}{\text{Total no. of div on circular head}}\\[0.5em]$

Here,

Pitch = 0.5 mm

Number of divisions on circular head = 50

Substituting the values in the formula above we get,

$\text {Least count} = \dfrac{0.5}{50} \\[0.5em] \text {Least count} = 0.01 \text {mm} \\[0.5em]$

Hence, the least count of the screw gauge = 0.01 mm

(iii) As we know,

Zero error = Coinciding Division x Least Count

Coinciding Division = 4

L.C. = 0.01 mm

Substituting the values in the formula above we get,

Zero error = 4 x 0.01 = + 0.04 mm

Hence, zero error, of the screw gauge = + 0.04 mm

Question 14

Figure below shows the reading obtained while measuring the diameter of a wire with a screw gauge. The screw advances by 1 division on main scale when circular head is rotated once.

Find —

(i) pitch of the screw gauge,

(ii) least count of the screw gauge, and

(iii) the diameter of the wire.

Answer

(i) As we know,

Pitch = distance moved ahead in 1 revolution

and given,

Distance covered in one revolutions = 1 mm

Hence, Pitch of the screw gauge = 1 mm

(ii) As we know,

$\text{Least count} = \dfrac {\text{Pitch}}{\text{Total no. of div on circular head}}\\[0.5em]$

Here,

Pitch = 1 mm

Number of divisions on circular head = 50

Substituting the values in the formula above we get,

$\text {Least count} = \dfrac{1}{50} \\[0.5em] \text {Least count} = 0.02 \text { mm} \\[0.5em]$

Hence, the least count of the screw gauge = 0.02 mm

(iii) As we know,

Diameter of the wire = main scale reading + circular scale reading     [Equation 1]

and

Circular scale reading = p x L.C.     [Equation 2]

p = 47

L.C. = 0.02 mm

Substituting the values in the Equation 2 we get,

Circular scale reading = 47 x 0.02 = 0.94 mm

Hence, circular scale reading = 0.94 mm and main scale reading = 4 mm.

Using Equation 1 we get,

Diameter of the wire = 4 mm + 0.94 mm = 4.94 mm

Hence, the diameter of the wire is 4.94 mm.

Question 15

A screw has a pitch equal to 0.5 mm. What should be the number of division on its head so as to read correct up to 0.001mm with its help?

Answer

As we know,

$\text {Least count} = \dfrac{\text{Pitch}}{\text{Total no. of div on circular head}} \\[0.5em]$

Given,

Pitch = 0.5 mm

L.C. = 0.001 mm

Substituting the values in the formula above we get,

$0.001\text{mm} = \dfrac{0.5}{\text{Total no. of div on circular head}} \\[0.5em] \Rightarrow \text{Total no. of div on circular head} = \dfrac{0.5}{0.001} \\[0.5em] \Rightarrow \text{Total no. of div on circular head} = 500$

Hence, total number of divisions on circular head = 500.

Exercise 1(C) — Multiple Choice Type

Question 1

The pendulum used in a clock is:

1. Simple pendulum
2. Compound pendulum
3. Second pendulum
4. None of these

Answer

Compound pendulum

Reason — Compound pendulums have a more constant period of oscillation over a wider range of amplitudes, making them suitable for use in clocks.

Question 2

The time taken to complete one oscillation is called:

1. Frequency
2. Amplitude
3. Time period
4. Acceleration

Answer

Time period

Reason — The time taken to complete one oscillation is called time period. It is denoted by T. Its unit is second (s).

Question 3

The number of oscillations made in one second is called :

1. Amplitude
2. Time period
3. Frequency
4. None of these

Answer

Frequency

Reason — The number of oscillations made in one second is called frequency. It is denoted by the letter f or n. Its unit is per second (s^-1) or hertz (Hz).

Question 4

The unit of time period is :

1. Hertz
2. Nanometre
3. Second
4. Centimetre

Answer

Second

Reason — The time taken to complete one oscillation is called time period. It is denoted by T. Its unit is second (s).

Question 5

The relationship between time period and frequency :

1. f = T
2. f = $\dfrac{1}{T}$
3. f = $\sqrt{T}$
4. None of these

Answer

f = $\dfrac{1}{T}$

Reason — If T is the time period of a simple pendulum, then,

In time T second, the number of oscillation is 1.

Therefore, in time 1 second, the number of oscillations will be $\dfrac{1}{T}$ which is the frequency f.

i.e., f = $\dfrac{1}{T}$ or T = $\dfrac{1}{f}$

Question 6

The maximum displacement of bob from its mean position on either side is called :

1. Period of oscillation
2. Frequency of oscillation
3. Amplitude
4. Oscillation

Answer

Amplitude

Reason — The maximum displacement of bob from its mean position on either side is called amplitude of oscillation. It is denoted by the letter a or A and is measured in metre (m).

Question 7

The effective length of a pendulum is related with time period as :

1. T² ∝ l²
2. T³ ∝ l
3. T² ∝ l
4. T ∝ L³

Answer

T² ∝ l

Reason — The time period of oscillation is directly proportional to the square root of its effective length i.e., T ∝ $\sqrt{l}$ or in other words, the square of time period of oscillation (T²) is directly proportional to its effective length (l) i.e., T² ∝ l.

Question 8

A simple pendulum is made by suspending a bob of mass 1 kg by a string of length l. Now if the length of this pendulum is increased to 4l, then its time period T will :

1. remain the same
2. become twice
3. become four times
4. become half

Answer

become twice

Reason — As T ∝ $\sqrt{l}$
When l₂ = 4l then,
T₂ ∝ $\sqrt{4l}$ = 2 $\sqrt{l}$ = 2T

Hence, time period T will become twice.

Question 9

The time period of a seconds' pendulum clock is —

1. 1 s
2. 2 s
3. 1 min
4. 12 h

Answer

2 s

Reason — A seconds' pendulum clock takes 1 second in moving from one extreme to the other extreme, so the time taken for one complete oscillation is 2 seconds. Hence, its time period is 2s.

Question 10

Time period of a simple pendulum is given by :

1. $T = 2 π \sqrt{\dfrac{g}{l}}$
2. $T = 2 π \sqrt{\dfrac{l}{g}}$
3. $T = 4 π \sqrt{\dfrac{l}{g}}$
4. $T = 4 π \sqrt{\dfrac{g}{l}}$

Answer

$T = 2 π \sqrt{\dfrac{l}{g}}$

Reason — Time period of a simple pendulum is given by $T = 2 π \sqrt{\dfrac{l}{g}}$

where

T = time period
l = effective length of pendulum
g = acceleration due to gravity.

Question 11

The time period of a simple pendulum depends on :

1. Length of pendulum
2. Amplitude of oscillation
3. Mass of bob
4. All of the above

Answer

Length of pendulum

Reason — The time period of oscillation is directly proportional to the square root of its effective length i.e., T ∝ $\sqrt{l}$ or in other words, the square of time period of oscillation (T²) is directly proportional to its effective length (l) i.e., T² ∝ l. Hence, we can say that, time period of a simple pendulum depends on length of pendulum.

Question 12

The time period of two pendulums of length 1 m and 16 m are in ratio :

1. 1 : 16
2. 1 : 4
3. 16 : 1
4. 4 : 1

Answer

1 : 4

Reason — As, T ∝ $\sqrt{l}$

$\dfrac{T_1}{T_2}$ = $\dfrac{\sqrt{l_1}}{\sqrt{l_2}}$

$\dfrac{T_1}{T_2}$ = $\dfrac{\sqrt{1}}{\sqrt{16}}$

$\dfrac{T_1}{T_2}$ = $\dfrac{1}{4}$

Question 13

The length of a simple pendulum is made one-fourth. Its time period becomes —

1. four times
2. one-fourth
3. double
4. half

Answer

half

Reason — Time period of a simple pendulum is given by:

$T = 2 π \sqrt{\dfrac{l}{g}} \\[0.5em]$

Time period is directly proportional to the square root of the length of the pendulum.

In the case when length is made one-fourth, we see that —

$T = 2 π \sqrt{\dfrac{l}{4\times g}} \\[0.5em] T = \dfrac{2}{2} \times π \sqrt{\dfrac{l}{g}} \\[0.5em] T = π \sqrt{\dfrac{l}{g}} \\[0.5em]$

Hence, we can say that when the length is made four times, time period of a simple pendulum is reduced to half.

Question 14

The length of a seconds' pendulum is nearly —

1. 0.5 m
2. 9.8 m
3. 1.0 m
4. 2.0 m

Answer

1.0 m

Reason — The effective length of a seconds' pendulum, at a place where g = 9.8 ms^-2 is nearly 1 meter.

Exercise 1(C) — Very Short Answer Type

Question 1

Define 'amplitude of oscillation'.

Answer

The maximum displacement of the bob from its mean position on either side is called the amplitude of oscillation.

Question 2

Define the terms: (i) oscillation (ii) amplitude (iii) frequency, and (iv) time period as related to a simple pendulum

Answer

(i) Oscillation – One complete to and fro motion of the bob of pendulum is called one oscillation.

(ii) Amplitude – The maximum displacement of the bob from its mean position on either side, is called the amplitude of oscillation. It is denoted by the letter a or A and is measured in metre(m).

(iii) Frequency – The number of oscillations made in one second is called the frequency. It is denoted by f or n. Its unit is per second (s^-1) or hertz (Hz).

(iv) Time period – The time taken to complete one oscillation is the time period. It is denoted by the symbol T. Its unit is in second (s).

Question 3

Name two factors on which the time period of a simple pendulum does not depend.

Answer

The time period of a simple pendulum does not depend on —

1. The mass or material of the body suspended (i.e., the bob).

2. The extent of swing on either side (i.e. on amplitude), provided the swing is not too large.

Question 4

How is the time period of a simple pendulum affected, if at all, in the following situations:

(a) The length is made four times,

(b) The acceleration due to gravity is reduced to one-fourth.

Answer

As we know that,

$T = 2 π \sqrt{\dfrac{l}{g}}$

where,

T = Time period

l = effective length of the pendulum

g = acceleration due to gravity.

(a) In the case when length is made four times, let time period be T₁, we see that —

$T_1 = 2 π \sqrt{\dfrac{4l}{g}} \\[0.5em] T_1= 2 \times 2 π \sqrt{\dfrac{l}{g}} \\[0.5em] T_1 = 2 \times T \\[0.5em]$

Hence, we can say that when the length is made four times, time period of a simple pendulum is doubled.

(b) In the case, when acceleration due to gravity is reduced to one fourth, let time period be T₁, we see that —

$T_1 = 2 π \sqrt{\dfrac{l}{\dfrac{g}{4}}} \\[0.5em] T_1 = 2 π \sqrt{\dfrac{4l}{g}} \\[0.5em] T_1 = 2 \times 2 π \sqrt{\dfrac{l}{g}} \\[0.5em] T_1 = 2 \times T \\[0.5em]$

Hence, we can say that when acceleration due to gravity is reduced to one fourth, time period of a simple pendulum is doubled.

Question 5

How are the time period T and frequency f of an oscillation of a simple pendulum related?

Answer

The time period (T) and frequency (f) of oscillation of a simple pendulum are related as stated below —

$\bold{f} = \dfrac{\bold{1}}{\bold{T}}$

Question 6

Two simple pendulum A and B have equal lengths, but heir bobs weigh 50 gf and 100 gf respectively. What would be the ratio of their time periods? Give reason for your answer.

Answer

As we know that,

$T = 2 π \sqrt{\dfrac{l}{g}}$

where,

T = Time period

l = effective length of the pendulum

g = acceleration due to gravity.

So we see that, time period does not depend on the weight of the bob.

As, lengths are equal so,

T₁ : T₂ = 1 : 1

Question 7

What is a seconds' pendulum?

Answer

A pendulum with a time period of oscillation equal to two seconds is known as the seconds pendulum. Its effective length, at a place, where g = 9.8 ms^-2 is nearly 1 meter.

Question 8

State the numerical value of the frequency of oscillation of a seconds’ pendulum. Does it depend on the amplitude of oscillation ?

Answer

As we know that,

$f = \dfrac{1}{T}$

and T for a seconds’ pendulum = 2s.

So, substituting the value of T in equation above we get,

$f = \dfrac{1}{2} \\[0.5em] \Rightarrow f = 0.5$

Hence, the numerical value of the frequency of oscillation of a seconds’ pendulum is 0.5 s^-1.

No, it does not depend on the amplitude of oscillation.

Exercise 1(C) — Short Answer Type

Question 1

What is a simple pendulum? Is the pendulum used in a pendulum clock simple pendulum? Give reason to your answer.

Answer

A simple pendulum is a heavy point mass (known as bob) suspended from a rigid support by a massless and inextensible string.

No, the pendulum used in the pendulum clock is not a simple pendulum, but it is a compound pendulum.(i.e., a body capable of oscillating about a horizontal axis passing through it.)

Question 2

Draw a neat diagram of a simple pendulum. Show on it the effective length of the pendulum and its one oscillation.

Answer

Below diagram shows the effective length and one oscillation of a simple pendulum:

Question 3

Name two factors on which the time period of a simple pendulum depends. Write the relation for the time period in terms of the above named factors.

Answer

Factors affecting the time period of a simple pendulum are —

1. Effective length of the pendulum — the time period of oscillation is directly proportional to the square root of its effective length.
   i.e., $T \propto \sqrt{l}$

2. Acceleration due to gravity — the time period of oscillations is inversely proportional to the square root of acceleration due to gravity
   i.e., $T \propto \dfrac{1}{\sqrt {g}}$

Relation between time period, effective length and acceleration due to gravity is as follows —

$T = 2\pi \sqrt{\dfrac{l}{g}}$

where,

T = Time period

l = effective length of the pendulum

g = acceleration due to gravity.

Question 4

How do you measure the time period of a given pendulum? Why do you note the time for more than one oscillation ?

Answer

To measure the time period of a given pendulum, we record the time for 20 or more oscillations and then divide the recorded time with the number of oscillations. Hence, we get the time period for one oscillation.

The time for more than one oscillation is noted, as the least count of stop watch is either 1s or 0.5s. It cannot record the time period in fraction such as 1.2s or 1.4s and so on.

Hence, it is made possible by noting the time t for 20 oscillations or more and then dividing it by the number of oscillations.

Question 5

Two simple pendulums A and B have lengths 1.0 m and 4.0 m respectively at a certain place. Which pendulum will make more oscillations in 1 minute? Explain your answer.

Answer

Given,

l_A = 1.0m
l_B = 4.0m

Since,

$T \propto \sqrt{l} \\[0.5em]$

∴,

$\dfrac {T_A}{T_B} = \dfrac{\sqrt{l_A}}{\sqrt{l_B}} \\[0.5em]$

Substituting the values of l in the formula above we get,

So,

$\dfrac {T_A}{T_B} = \dfrac{\sqrt{1}}{\sqrt{4}} \\[0.5em] \Rightarrow \dfrac {T_A}{T_B} = \dfrac{1}{2} \\[0.5em]$

i.e., T₁ : T₂ = 1 : 2

∴, time period of B is more (twice) than that of A. Hence, A will make more oscillations (twice) in a given time than B.

Question 6

State how does the time period of a simple pendulum depend on —

(a) length of pendulum,

(b) mass of bob,

(c) amplitude of oscillation and

(d) acceleration due to gravity.

Answer

The time period of a simple pendulum varies as follows —

(a) Length of pendulum (l) — Time period of a simple pendulum is directly proportional to the square root of the length of the pendulum.

$T \propto \sqrt{l}$

(b) Mass of bob — Time period of a simple pendulum is independent of the mass of the bob.

(c) Amplitude of oscillation — Time period of a simple pendulum is independent of the amplitude of oscillation

(d) Acceleration due to gravity (g) — Time period of a simple pendulum is inversely proportional to the the square root of acceleration due to gravity .

$T \propto \sqrt{\dfrac{1}{g}}$

Exercise 1(C) — Long Answer Type

Question 1

How does the time period (T) of a simple pendulum depend on its length (l) ? Draw a graph showing the variation of T² with l. How will you use this graph to determine the value of g (acceleration due to gravity)?

Answer

Time period of a simple pendulum is directly proportional to the square root of its effective length.

i.e., T ∝ $\sqrt{l}$

Graph showing the variation of T² with l is given below:

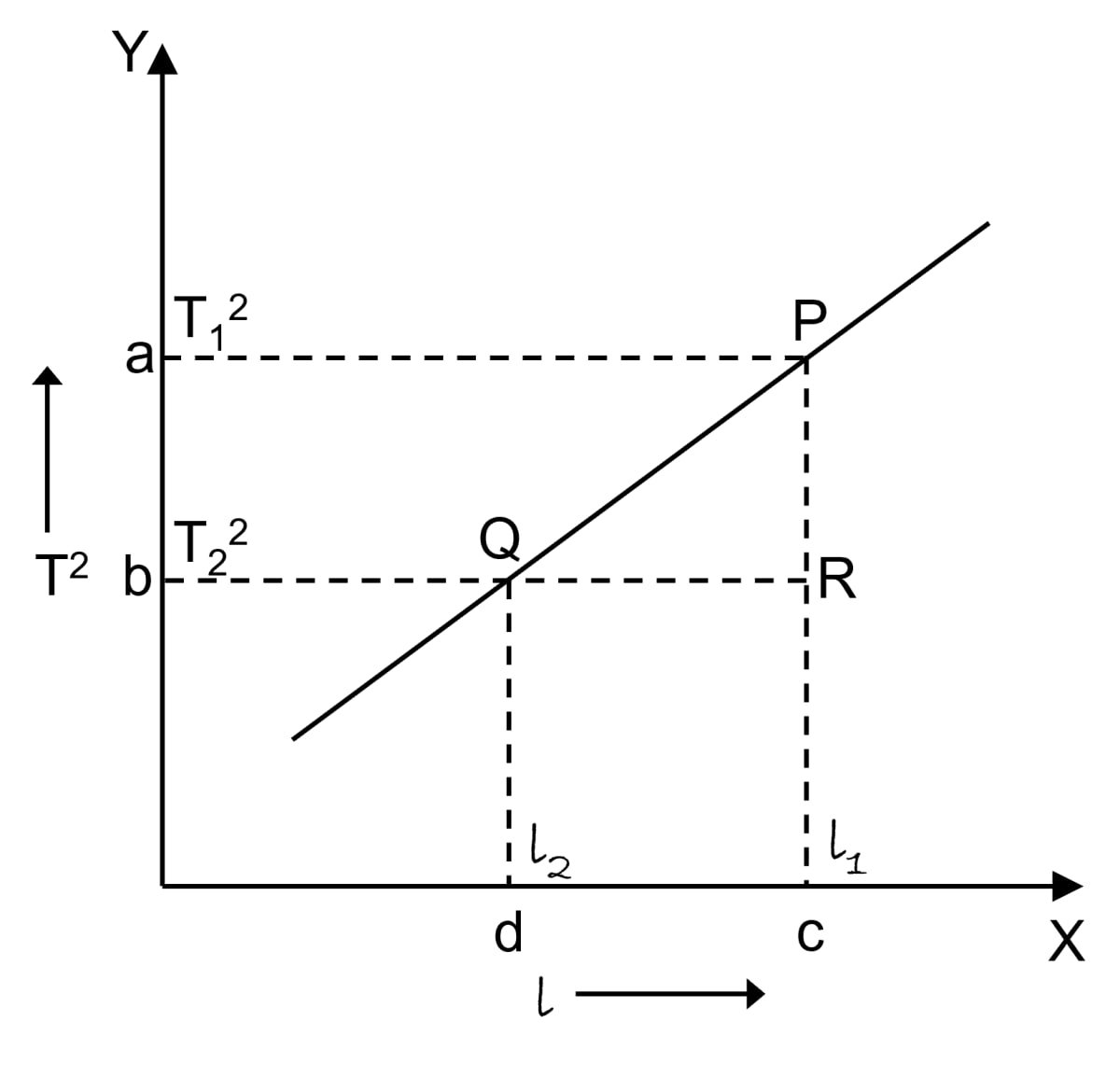
In order to find the acceleration due to gravity with the help of the above graph, we follow the following steps —

The slope of the straight line obtained in the T² vs l graph, as shown in fig, can be obtained by taking two points P and Q on the straight line and drawing normals from these points on the X and Y axes. Then, note the value of T², say T₁² and T₂² at a and b respectively, and also the value of l say l₁ and l₂ respectively at c and d.

Then,

$\text{Slope} = \dfrac{PR}{QR} = \dfrac{ab}{cd} = \dfrac{T_1^2 - T_2^2}{l_1 - l_2}$

This slope is found to be a constant at a place and,

$\text{Slope} = \dfrac{4π^2}{g}$

where, g = acceleration due to gravity at that place.

Thus, g can be determined at a place from the graph using the following relation,

$g = \dfrac{4π^2}{\text{Slope of } T^2 \text{ vs l graph}}$

Exercise 1(C) — Numericals

Question 1

A simple pendulum completes 40 oscillations in one minute.

Find its —

(a) frequency,

(b) time period.

Answer

(a) Given,

40 oscillations in one minute, so

$\text {frequency per second} = \dfrac{40}{60} \\[0.5em] = \dfrac{2}{3} \\[0.5em] = \text {0.67} s^{-1} \\[0.5em]$

Hence, frequency of oscillation = 0.67 s^-1.

(b) As we know that,

$T = \dfrac{1}{f}$

So, substituting the value of f = 0.67 s^-1, in equation above we get,

$T = \dfrac{1}{0.67} \\[0.5em] \Rightarrow T = 1.49253s \approx 1.5s \\[0.5em]$

Hence, time period of the simple pendulum is 1.5 s.

Question 2

The time period of a simple pendulum is 2s. What is its frequency? What name is given to such a pendulum?

Answer

As we know that,

$f = \dfrac{1}{T}$

Given,

T = 2s

So, substituting the value of T in equation above we get,

$f = \dfrac{1}{2} \\[0.5em] \Rightarrow f = 0.5$

Hence, the frequency of oscillation of the simple pendulum is 0.5 s^-1.

The name given to such a pendulum is seconds' pendulum.

Question 3

A seconds' pendulum is taken to a place where acceleration due to gravity falls to one forth. How is the time period of the pendulum affected, if at all? Give reason. What will be its new time period?

Answer

As we know,

$T = 2 π \sqrt{\dfrac{l}{g}}$

We observe that time period is inversely proportional to the square root of acceleration due to gravity.

Hence, when 'g' falls to one-fourth, time period increases.

When acceleration due to gravity is reduced to one fourth, we see that —

$T = 2 π \sqrt{\dfrac{l}{\dfrac{g}{4}}} \\[0.5em] T = 2 π \sqrt{\dfrac{4l}{g}} \\[0.5em] T = 2 \times 2 π \sqrt{\dfrac{l}{g}} \\[0.5em]$

Hence, we can say that when acceleration due to gravity is reduced to one fourth, time period of a simple pendulum doubles.

As, the given pendulum is a seconds' pendulum so T = 2s

∴ New T = 2 x 2 = 4s

Question 4

Find the length of a seconds' pendulum at a place where g = 10 ms^-2 (Take π = 3.14).

Answer

As we know,

$T = 2 π \sqrt{\dfrac{l}{g}}$

Given,

g = 10 ms^-2

π = 3.14

T = 2 s

Substituting the values in the formula above we get,

$2 = 2 \times 3.14 \sqrt{\dfrac{l}{10}} \\[0.5em] \Rightarrow (\dfrac{2}{2 \times 3.14}) = \sqrt{\dfrac{l}{10}} \\[0.5em] \Rightarrow (\dfrac{2}{2 \times 3.14})^2 = \dfrac{l}{10} \\[0.5em] \Rightarrow (\dfrac{1}{3.14})^2 = \dfrac{l}{10} \\[0.5em] \Rightarrow (0.3184)^2 = \dfrac{l}{10} \\[0.5em] \Rightarrow 0.10142 = \dfrac{l}{10} \\[0.5em] \Rightarrow l = 1.0142 \\[0.5em]$

Hence, length of a seconds’ pendulum = 1.0142 m

Question 5

Compare the time periods of two pendulums of length 1m and 9m.

Answer

As we know that,

$T = 2 π \sqrt{\dfrac{l}{g}} \\[0.5em]$

Time period is directly proportional to the square root of the length of the pendulum.

In the case when length is 1m,

$T_1 = 2 π \sqrt{\dfrac{1}{g}} \\[0.5em]$

and

In the case when length is 9m,

$T_2 = 2 π \sqrt{\dfrac{9}{g}} \\[0.5em]$

So, comparison of T₁ and T₂ gives —

$T_1 : T_2 = 2 π \sqrt{\dfrac{1}{g}} : 2 π \sqrt{\dfrac{9}{g}} \\[0.5em] T_1 : T_2 = \sqrt{\dfrac{1}{9}} \\[0.5em] \Rightarrow T_1 : T_2 = \dfrac{1}{3} \\[0.5em]$

Hence, T₁ : T₂ = 1 : 3

Question 6

A pendulum completes 2 oscillations in 5s.

(a) What is its time period?

(b) If g = 9.8 ms^-2, find its length.

Answer

Given,

2 oscillations in 5 seconds, so

$\text {frequency per second} = \dfrac{2}{5} \\[0.5em] \Rightarrow \text {frequency per second} = \text {0.4 hertz} \\[0.5em]$

Hence, frequency of oscillation = 0.4 hertz.

As we know that,

$T = \dfrac{1}{f}$

So, substituting the value of f = 0.4 hertz, in equation above we get,

$T = \dfrac{1}{0.4} \\[0.5em] \Rightarrow T = 2.5s \\[0.5em]$

Hence, time period of pendulum is 2.5 s

(b) As we know,

$T = 2 π \sqrt{\dfrac{l}{g}} \\[0.5em]$

Given,

g = 9.8 ms^-2

and we know,

π = 3.14

T = 2.5 s

Substituting the values in the formula above we get,

$2.5 = 2 \times 3.14 \sqrt{\dfrac{l}{9.8}} \\[0.5em] \Rightarrow (\dfrac{2.5}{2 \times 3.14}) = \sqrt{\dfrac{l}{9.8}} \\[0.5em] \Rightarrow (\dfrac{2.5}{2 \times 3.14})^2 = \dfrac{l}{9.8} \\[0.5em] \Rightarrow (\dfrac{2.5}{6.28})^2 = \dfrac{l}{9.8} \\[0.5em] \Rightarrow (0.398)^2 = \dfrac{l}{9.8} \\[0.5em] \Rightarrow 0.158 = \dfrac{l}{9.8} \\[0.5em] \Rightarrow l = 9.8 \times 0.158 \\[0.5em] \Rightarrow l = 1.55$

Hence, length of a seconds’ pendulum = 1.55 m

Question 7

The time periods of two simple pendulums at a place are in the ratio 2:1. What will be the ratio of their lengths ?

Answer

As we know that,

$T = 2 π \sqrt{\dfrac{l}{g}} \\[0.5em]$

Time period is directly proportional to the square root of the length of the pendulum.

In the case when,
T₁ : T₂ = 2 : 1     [Equation 1]

we know that,

T₁ : T₂ = $\sqrt{l_1} : \sqrt{l_2}$     [Equation 2]

So we get,

$\sqrt{l_1} : \sqrt{l_2} = 2 : 1 \\[0.5em] \Rightarrow \dfrac{\sqrt{l_1}}{\sqrt{l_2}} = \dfrac{2}{1}$

Squaring both sides we get,

$\dfrac{l_1}{l_2} = \dfrac{2^2}{1^2} \\[0.5em] \Rightarrow \dfrac{l_1}{l_2} = \dfrac{4}{1} \\[0.5em] \Rightarrow l_1 : l_2 = 4 : 1$

Hence, ratio of lengths = 4 : 1

Question 8

It takes 0.2s for a pendulum bob to move from mean position to one end. What is the time period of pendulum?

Answer

As we know that,

Time period = 4 x (time a pendulum bob takes to move from mean position to one end).

Given,

Time a pendulum bob takes to move from mean position to one end = 0.2s

Substituting the value in the equation above we get,

Time taken to complete one oscillation(T) —

$= (4 \times 0.2)s \\[0.5em] = 0.8s \\[0.5em]$

Hence, time period of the pendulum = 0.8s

Question 9

How much time does the bob of a seconds' pendulum take to move from one extreme of its oscillation to the other extreme?

Answer

As we know that, the time period of a seconds' pendulum is 2s.

So, time taken for a seconds’ pendulum to move from one extreme to other is equal to the half of time period.

$T_{half} = \dfrac{T}{2} \\[0.5em] \Rightarrow T_{half} = \dfrac{2}{2} = 1s \\[0.5em]$

Hence, time taken for a seconds' pendulum to move from one extreme to other extreme = 1s