Which of the following is a scalar quantity?
- Force
- Time
- Acceleration
- Displacement
Answer
Time
Reason — Time has only magnitude, whereas force, acceleration and displacement all have magnitude as well as direction.
A vector quantity possesses :
- Direction
- Magnitude
- Both (a) and (b)
- None of these
Answer
Both (a) and (b)
Reason — Vector quantities have both magnitude and direction.
A vector quantity is —
- Work
- Pressure
- Distance
- Velocity
Answer
Velocity
Reason — A vector quantity has both magnitude and direction. Velocity has both magnitude and direction, so it is a vector quantity.
The motion of a train on a straight track is an example of ............... motion.
- Two dimensional
- Three dimensional
- One dimensional
- All of these
Answer
One dimensional
Reason — As the train is moving on a straight track and there is no lateral movement (sideways), hence it is a one dimensional motion.
If a body starts its motion from point A to B and comes back to the same point after a certain time interval, the displacement is :

- 10
- 20
- 0
- 15
Answer
0
Reason — If a body starts its motion from point A to B and comes back to the same point after a certain time interval, the displacement is 0. For example: In a circular motion, the body comes back to the starting point after completing the circle, then displacement is zero but distance covered is not zero.
Motion of a car in a crowded street is an example of :
- Uniform speed
- Uniform velocity
- Variable acceleration
- Uniform acceleration
Answer
Variable acceleration
Reason — As the change in velocity of the car in not same in same interval of time, the acceleration is said to be variable.
The distance travelled by a body in 10 s when it travels with a uniform speed of 10 ms-1 is :
- 100 m
- 1 m
- 20 m
- 50 m
Answer
100 m
Reason — As the body is moving with uniform speed, equal distance is covered in equal intervals of time.
Distance covered in 1 s is 10 m, hence distance covered in 10 s is 10 x 10 = 100 m.
For a particle in motion, which of the following quantity can be zero at any given instant?
- Displacement
- Distance
- Speed
- None of these
Answer
Displacement
Reason — If a body starts its motion from point A to B and comes back to the same after a certain time interval, the displacement is 0. Whereas, distance covered and speed will not be zero.
18 km h-1 is equal to —
- 10 m s-1
- 5 m s-1
- 18 m s-1
- 1.8 m s-1
Answer
5 m s-1
Reason — As,
Hence, 18 km h-1 is equal to 5 ms-1.
The value of g does not depend on the :
- Height of the body
- Mass of the body
- Shape of the body
- All of these
Answer
All of these
Reason — The value of g does not depend on height, mass or shape of the body. On the earth's surface, g is maximum at the poles and minium at the equator. The value of g decreases with altitude and also with depth from the earth's surface.
Free fall of a body near earth's surface is an example of :
- Uniform acceleration
- Uniform velocity
- Variable acceleration
- None of these
Answer
Uniform acceleration
Reason — When a body is falling freely, the acceleration is said to be uniform as equal changes in velocity takes place in equal intervals of time.
The value of g is maximum at :
- Tropic of capricorn
- Equator
- Tropic of cancer
- Poles
Answer
Poles
Reason — On the earth's surface, g is maximum at the poles and minium at the equator. The value of g decreases with altitude and also with depth from the earth's surface.
A body when projected up with an initial velocity u goes to a maximum height h in time t and then comes back at the point of projection. The correct statement is —
- The average velocity is 2h/t
- The acceleration is zero
- The final velocity on reaching the point of projection is 2u
- The displacement is zero
Answer
The displacement is zero
Reason — The displacement is zero because the initial and the final position of the body is same.
Identify the correct statement from the following :
The average speed of a body can be zero even if it's average velocity is not zero.
Speed and velocity both are scalar quantities.
The magnitude of velocity of a body in motion is its speed.
Speed and velocity can be positive or negative depending upon the direction of motion.
Answer
The magnitude of velocity of a body in motion is its speed
Reason —
(1) Incorrect — Average speed is the total distance travelled divided by time, and is never zero unless the body doesn’t move at all. On the other hand, average velocity can be zero if the displacement is zero (like in a round trip).
(2) Incorrect — Speed is a scalar quantity, but velocity is a vector quantity as it has both magnitude and direction.
(3) Correct — The magnitude of velocity is the same as the speed of the body.
(4) Incorrect — Speed is always positive or zero (since it's a scalar quantity) but velocity can be positive or negative depending on the direction.
A car travels the first th part of its total distance with a speed v1, and the remaining th of the distance with speed v2. Its average speed is :
Answer
Reason — Let, total distance covered be S of which S1 is covered with v1 in time t1 and S2 with v2 in time t2.
Then,
............... (1)
and
............... (2)
As
Then,
Putting value of S1 from equation 1
Similarly
Putting value of S2 from equation 2
Now,
State whether the following quantity is a scalar or vector?
(a) Pressure
(b) Force
(c) Momentum
(d) Energy
(e) Weight
(f) Speed
Answer
(a) Pressure — Scalar quantity
(b) Force — Vector quantity
(c) Momentum — Vector quantity
(d) Energy — Scalar quantity
(e) Weight — Vector quantity
(f) Speed — Scalar quantity
Write the parameters required to express a scalar quantity.
Answer
Two parameters are required to express a scalar quantity :
- Unit in which the quantity is being expressed.
- Numerical value of the measured quantity.
Name the parameters required to express a vector quantity.
Answer
Three parameters are required to express a vector quantity :
- Unit in which the quantity is being expressed.
- Numerical value of the measured quantity.
- Direction.
What does the negative sign with a vector quantity indicates?
Answer
The negative sign with a vector quantity implies the reverse (or opposite) direction. e.g., the forces and are in opposite directions.
When is a body said to be at rest ?
Answer
A body is said to be at rest if it does not change its position with respect to its immediate surrounding.
When is a body said to be in motion ?
Answer
A body is said to be in motion if it changes its position with respect to its immediate surroundings.
What do you mean by motion in one direction ?
Answer
When a body moves along a straight line path, its motion is said to be one dimensional motion.
Define displacement. State its unit.
Answer
The shortest distance from the initial to the final position of the body, is the magnitude of displacement and its direction is from initial position to the final position. It is a vector quantity.
Unit — The S.I. unit of displacement is metre (m) and C.G.S. unit is centimetre (cm)
When is the magnitude of displacement equal to the distance?
Answer
The magnitude of displacement is equal to the distance, when the motion is in a fixed direction.
Define velocity. State its unit.
Answer
The velocity of a body is the distance travelled per second by the body in a specified direction.
It is a vector quantity.
.
Define speed. What is its S.I. unit ?
Answer
Speed of a body is the rate of change of distance with time .
It is a scalar quantity. It is generally represented by u or v .
If a body travels a distance S in time t, then its speed v is —
.
Which quantity speed or velocity gives the direction of motion of a body.
Answer
Velocity gives direction of motion of body as it is a vector quantity. Speed is a scalar quantity hence, it does not say anything about direction of motion.
When is the instantaneous speed same as the average speed?
Answer
In case of a body moving with uniform speed, the instantaneous speed and the average speed are equal (same as the uniform speed) because, in case of uniform speed, neither the speed nor the direction change.
Define acceleration. State its S.I. unit.
Answer
Acceleration is the rate of change of velocity with time.
Numerically, acceleration is equal to the change in velocity in 1 s.
i.e.,
What is meant by the term retardation? Name its S.I. unit.
Answer
If the velocity of a body decreases with time, it is called retardation. As it is decrease in velocity per second, so, retardation is negative acceleration.
It's unit is same as that of acceleration.
Which of the quantity, velocity or acceleration determines the direction of motion ?
Answer
Velocity determines the direction of motion as velocity is the distance travelled per second by a moving object in a particular direction.
Positive or negative sign of velocity indicates the direction of motion.
Acceleration is the rate of change of velocity with time. It does not say anything about direction of motion.
Positive or negative sign of acceleration tell us whether the velocity is increasing or decreasing.
Define the term acceleration due to gravity. State its average value.
Answer
When a body falls freely under the gravity, the acceleration produced in the body due to earth's gravitational attraction is called acceleration due to gravity.
The average value of 'g' is 9.8 ms-2 (or nearly 10 ms-2).
Differentiate between scalar and vector quantities, giving two examples of each.
Answer
Differences between scalar and vector quantities are as follows —
| Scalar Quantity | Vector Quantity |
|---|---|
| These are physical quantities which are expressed only by their magnitude. | These physical quantities require magnitude as well as the direction to express them, then only their meaning is complete. |
| We need two parameters to express a scalar quantity. | We require three parameters to express a vector quantity. |
| The parameters are: (i) unit in which the quantity is being measured (ii) numerical value of the measured quantity. | The parameters are: (i) unit (ii) direction (iii) numerical value of quantity. |
| Scalar quantities can be added, subtracted, multiplied and divided by simple arithmetic methods. | Vector quantities follow different algebra for their addition, subtraction, multiplication and division. |
| Example : (i) If we say, mass of a body is 5 kg, it has a complete meaning and we are completely expressing the mass of the body. (ii) mass, length, time, etc. | Example : (i) A body is displaced by 5 metre towards east, then it has a complete meaning. (ii) velocity, acceleration, force, etc. |
Both scalar and vector quantities can be added, subtracted, multiplied and divided by simple arithmetic methods. Is this statement correct? Give a reason for your answer.
Answer
No, the statement is not correct. Scalar quantities can be added, subtracted, multiplied and divided by simple arithmetic methods however vector quantities follow different algebra for their addition, subtraction and multiplication as they have magnitude as well as direction.
Differentiate between the following :
(a) distance and displacement
(b) speed and velocity
(c) uniform velocity and variable velocity
(d) average speed and average velocity
(e) acceleration and retardation
(f) uniform acceleration and variable acceleration
Answer
(a) The difference between distance and displacement is as follows :
| Distance | Displacement |
|---|---|
| It is the length of the path traversed by the object in a certain time. | It is the distance travelled by the object in a specified direction in a certain time (i.e. it is the shortest distance between the final and the initial positions). |
| It is a scalar quantity i.e., it has only the magnitude. | It is a vector quantity i.e., it has both magnitude and direction. |
| It depends on the path followed by the object. | It does not depend on the path followed by the object. |
| It is always positive. | It can be positive or negative depending on its direction. |
| It can be more than or equal to the magnitude of displacement. | Its magnitude can be less than or equal to the distance, but can never be greater than the distance. |
| It may not be zero even if displacement is zero, but it can not be zero if displacement is not zero. | It is zero if distance is zero, but it can be zero if distance is not zero. |
(b) The difference between speed and velocity is as follows :
| Speed | Velocity |
|---|---|
| The distance travelled per second by a moving object is called its speed. | The distance travelled per second by a moving object in a particular direction is called its velocity. |
| It is a scalar quantity. The speed does not tell us the direction of motion. | It is a vector quantity. The velocity tells us the speed as well as the direction of motion. |
| The speed is always positive since direction is not taken into consideration. | The velocity can be positive or negative depending upon the direction of motion. |
| After one round in a circular path, the average speed is not zero. | After completing each round in a circular path, the average velocity is zero. |
(c) The difference between uniform velocity and variable velocity is as follows :
| Uniform Velocity | Variable Velocity (or non-uniform) |
|---|---|
| If a body travels equal distances in a particular direction, in equal intervals of time, the body is said to be moving with a uniform velocity. | If a body moves unequal distances in a particular direction in equal intervals of time or it moves equal distances in equal intervals of time, but its direction of motion does not remain the same, then the velocity of the body is said to be variable (non-uniform). |
| Example — A body, once started on a frictionless surface, moves with uniform velocity. | Example — The motion of a body in circular path, even with uniform speed is with variable velocity as the direction of motion of body continuously changes with time. |
(d) The difference between average speed and average velocity is as follows :
| Average Speed | Average Velocity |
|---|---|
| The ratio of the total distance travelled by the body to the total time of journey is called its average speed. | If the velocity of a body moving in a particular direction changes with time, the ratio of displacement to the time taken in the entire journey is called its average velocity. |
| Avg Speed = | Avg Velocity = |
| Average speed can never be zero. | It can be zero, even if average speed is a non-zero value. |
(e) The differences between acceleration and retardation are as follows :
| Acceleration | Retardation |
|---|---|
| If the velocity of a body increases with time, it is called acceleration. | If the velocity of a body decreases with time, it is called retardation. |
| As it is increase in velocity per second so it is positive acceleration. | As it is decrease in velocity per second so retardation is negative acceleration. |
(f) The differences between uniform acceleration and variable acceleration are as follows :
| Uniform Acceleration | Variable acceleration |
|---|---|
| The acceleration is said to be uniform (or constant) when equal changes in velocity take place in equal intervals of time. | If changes in velocity are not same in the same intervals of time, the acceleration is said to be variable. |
| Example — The motion of a body under gravity (e.g., free fall of a body) | Example — The motion of a vehicle on a crowded (or hilly) road. |
Can displacement be zero even if distance is not zero? Give one example to explain your answer.
Answer
Yes, the displacement can be zero, even if the distance is not zero.
If a body, after travelling, comes back to its starting point, the displacement is zero but the distance travelled is not zero.
Example — When a body is thrown vertically upwards from a point A on the ground, after some time it comes back to the same point A, then the displacement of the body is zero but the distance travelled by the body is not zero.
Give an example of motion of a body moving with a constant speed, but with a variable velocity. Draw a diagram to represent such a motion.
Answer
The motion of a body in circular path, is an example of a body moving with a constant speed and variable velocity because the direction of motion of body changes continuously with time.
At any instant, the velocity is along the tangent to the circular path at that point.

The figure above shows the direction of velocity v at different points A, B, C and D of the circular path.
Give an example of motion in which average speed is not zero, but average velocity is zero.
Answer
If a body starts its motion and comes back to the same point after a certain time, (e.g., in a circular motion,) the displacement is zero, so the average velocity is also zero, but the total distance travelled is not zero and therefore, the average speed is not zero.
Give one example of each of the following :
(a) Uniform velocity
(b) Variable velocity
(c) Variable acceleration
(d) Uniform retardation
Answer
(a) Uniform velocity — The rain drops reach on earth’s surface falling with uniform velocity.
(b) Variable velocity — The motion of a freely falling body is with variable velocity because although the direction of motion of the body does not change, but the speed continuously increases.
(c) Variable acceleration — The motion of a vehicle on a hilly (or crowded) road.
(d) Uniform retardation — Motion of a vehicle, reaching a destination.
The diagram below shows the pattern of the oil on the road, dripping at a constant rate from a moving car. What information do you get from it about the motion of car?

Answer
With the help of the given diagram, we observe that the red dots (dripping oil) are initially at regular intervals and later the gap between the dots decreases, which implies that initially the car was covering equal distances in equal intervals of time but later the distance is decreasing.
Thus, we can infer that initially the car is moving with a constant speed and then it slows down.
What is the direction of velocity of an object moving in a circular path?
Answer
The direction of velocity of an object moving in a circular path is always tangent to the circle. This means that with the movement of body the velocity changes.
'The value of g remains same at all places on the earth surface'. Is this statement true? Give reason for your answer.
Answer
No, the value of 'g' is not same at all places on the earth's surface. The value of g varies from place to place so an average value is considered. The average value of 'g' is 9.8 ms-2 or nearly 10 ms-2. The value of g decreases with altitude and also with depth from the earth's surface.
The value of 'g' is maximum at the poles and minimum at the equator on the earth surface.
If a stone and a pencil are dropped simultaneously in vacuum from the top of a tower, which of the two will reach the ground first ? Give reason.
Answer
Both will reach the ground simultaneously as value of g does not depend on the mass of the body. Acceleration due to gravity is same ( = g ) on both and there is no effect of friction and buoyancy due to air.
The speed of a car is 72 km h-1. Express it in m s-1.
Answer
As,
Hence, 72km h-1 is equal to 20 m s-1.
Express 15 m s-1 in km h-1 .
Answer
As,
Hence, 15 m s-1 is equal to 54 kmh-1.
Express each of the following in m s -1 —
(a) 10 km h-1
(b) 18 km min-1
Answer
(a) As,
Hence, 10 km h-1 is equal to 2.78 ms-1.
(b) As,
Hence, 18 km h-1 is equal to 300 m s-1.
Arrange the following speeds in increasing order — 10 m s-1, 1 km min-1, 18 km h-1.
Answer
In order to arrange in increasing order of speeds, the units of the given speeds must be same.
Hence, we convert all the three in m s-1.
(a) 10 m s-1 = 10 m s-1 .... [1]
(already in m s-1)
(b) 1 km min-1,
Hence,
1 km min-1 = 16.66 m s-1 .... [2]
(c) 18 km h-1,
As,
Hence,
18km h-1 = 5 m s-1 .... [3]
From 1, 2 and 3, we get the increasing order as follows —
18 km h-1, 10 m s-1, 1 km min-1.
A train takes 3 h to travel from Agra to Delhi with a uniform speed of 65 km h-1. Find the distance between the two cities.
Answer
As we know,
Distance = Speed x Time
Given,
time = 3 h
speed = 65 km h-1
Substituting the values in the formula above, we get,
Distance = 65 x 3 = 195 km
Hence, the distance between the two cities = 195 km.
A car travels first 30 km with a uniform speed of 60 km h-1 and then next 30 km with a uniform speed of 40 km h -1.
Calculate —
(i) the total time of journey,
(ii) the average speed of the car.
Answer
Given,
Distance travelled S1 = 30 km
Speed v1 = 60 km h-1
Distance travelled S2 = 30 km
Speed v2 = 40 km h-1
(i) As we know,
Substituting the values in the formula above, we get,
Converting 0.5 h to min we get,
and
Converting 0.75 h to min we get,
Total time t = t1 + t2
= 30 min + 45 min
= 75 min
Hence, Total time of journey = 75 min.
(ii) As we know,
Total distance S = S1 + S2
= 30 km + 30 km
= 60 km
Hence, Total distance travelled = 60 km.
As we know,
Hence, Average speed of the car = 48 kmh-1
A train takes 2 h to reach station B from station A, and then 3 h to return from station B to station A. The distance between the two stations is 200 km.
Find —
(i) The average speed
(ii) The average velocity of the train
Answer
Given,
Distance travelled S1 = 200 km
time t1 = 2 h
Distance travelled S2 = 200 km
time t2 = 3 h
(i) As we know,
Total distance travelled S = S1 + S2
= 200 km + 200 km
= 400 km
Total time taken t = t1 + t2
= 2 h + 3 h
= 5 h
Substituting the values of total distance travelled and total time taken in the formula of Average Speed above, we get,
Hence, Average speed of the car = 80 km h-1
(ii) Displacement = 0 (since final position is same as initial position)
Hence, Average velocity = 0 ( as displacement = 0)
A car moving on a straight path covers a distance of 1 km due east in 100 s.
What is
(i) the speed and
(ii) the velocity of car ?
Answer
As we know,
Given,
Distance travelled S = 1 km = 1000 m,
time t = 100 s
Substituting the values in the formula above, we get,
Hence, speed of the car is 10 m s-1
(ii) The magnitude of velocity of the car is same as that of speed of car i.e., 10 m s-1
However, when we talk about velocity, we mention direction also.
Hence, velocity of car is 10 m s-1 due east.
A body starts from rest and acquires a velocity 10 m s -1 in 2 s. Find its acceleration.
Answer
Given,
Initial velocity (u) = 0
Final velocity (v) = 10 m s -1
Time (t) = 2 s
As we know,
Substituting the values in the formula above, we get,
Hence, acceleration of the body is 5 m s -2.
A car starting from rest acquires a velocity of 180 m s-1 in 0.05 h. Find the acceleration.
Answer
As we know,
Given,
Initial velocity (u) = 0
Final velocity (v) = 180 m s -1
Time (t) = 0.05 h
Converting 0.05 h to s we get,
Substituting the values in the formula above, we get,
Hence, acceleration of the body is 1 m s -2.
A body is moving vertically upwards. Its velocity changes at a constant rate from 50 m s -1 to 20 m s -1 in 3 s . What is its acceleration ?
Answer
As we know,
Given,
Initial velocity (u) = 50 m s -1
Final velocity (v) = 20 m s -1
Time (t) = 3 s
Substituting the values in the formula above, we get,
Hence, acceleration of the body is -10 m s -2. Negative sign shows that the velocity decreases with time, so retardation is 10 m s -2.
A toy car initially moving with a uniform velocity of 18 km h-1 comes to a stop in 2 s. Find the retardation of the car in S.I. units.
Answer
As we know,
Given,
Initial velocity (u) = 18 km h-1
To convert initial velocity u to m s-1
Hence, 18 km h-1 is equal to 5 m s-1.
Final velocity (v) = 0
Time (t) = 2 s
Substituting the values in the formula above, we get,
Hence, acceleration of the body is -2.5 m s -2. Negative sign shows that the velocity decreases with time, so retardation is 2.5 m s -2.
A car accelerates at a rate of 5 m s-2. Find the increase in its velocity in 2 s.
Answer
As we know,
Hence,
Given,
a = 5 m s-2
t = 2 s
Substituting the values in the formula above, we get,
Hence, increase in velocity = 10 m s -1.
A car is moving with a velocity 20 m s -1 . The brakes are applied to retard it at a rate of 2 m s -2. What will be the velocity after 5 s of applying the brakes ?
Answer
As we know,
and retardation is negative acceleration.
Hence,
Given,
a = - 2 m s-2
t = 5 s
u = 20 m s -1
Substituting the values in the formula above, we get,
Hence, final velocity = 10 m s -1.
A bicycle initially moving with a velocity 5.0 m s -1 accelerates for 5 s at a rate of 2 m s-2 . What will be its final velocity?
Answer
As we know,
Hence,
Given,
a = 2 m s-2
t = 5 s
u = 5.0 m s -1
Substituting the values in the formula above, we get,
Hence, final velocity = 15 m s -1.
A car is moving in a straight line with speed 18 km h-1. It is stopped in 5s by applying the brakes.
Find —
(i) the speed of car in m s -1,
(ii) the retardation and
(iii) the speed of car after 2 s of applying the brakes .
Answer
Given,
speed of car = 18 km h-1
(i) To convert speed to m s-1
Hence, 18 km h-1 is equal to 5 m s-1.
(ii) As the car is stopped, the final velocity (v) = 0
initial velocity (u) = 18 km h-1
As we know,
Given,
Initial velocity (u) = 5 m s-1
Final velocity (v) = 0
Time (t) = 5 s
Substituting the values in the formula above, we get,
Hence, acceleration of the car is -1 m s-2. Negative sign shows that the velocity decreases with time, so retardation is 1 m s -2.
(iii) Given,
t = 2 s
a = -1 m s-2
u = 5 m s-1
Substituting the values in the formula for acceleration, we get,
Hence, the speed of car after 2 s of applying the brakes = 3 m s-1.
Give an example of motion of a body moving with a constant speed, but with a variable velocity. Draw a diagram to represent such a motion.
Answer
The motion of a body in circular path, is an example of a body moving with a constant speed and variable velocity because the direction of motion of body changes continuously with time.
At any instant, the velocity is along the tangent to the circular path at that point.

The figure above shows the direction of velocity v at different points A, B, C and D of the circular path.
The slope of displacement-time graph gives :
- Velocity
- Acceleration
- Speed
- Displacement
Answer
Velocity
Reason — As, velocity is the ratio of displacement and time, therefore, the slope of displacement-time graph gives the velocity.
From the given displacement-time graph, answer the following questions:

(i) The kind of motion depicted in this graph is :
- uniform
- non-uniform
- retardation
- all of the above
(ii) The velocity between point A and C is:
- 20 ms-1
- 5 ms-1
- 10 ms-1
- 15 ms-1
(iii) The displacement at t = 3s is:
- 15 m/s2
- 12.5 m/s2
- 40 m
- 30 m
Answer
(i) uniform
Reason — As the graph shows the linear relationship between displacement and time i.e., the car travels equal distance in equal intervals of time in a certain direction. Thus, it is moving with uniform motion.
(ii) 10 ms-1
Reason — As, velocity is the ratio of displacement and time, therefore,
(iii) 40 m
Reason — When we observe the graph, we notice that at t = 3 s, the displacement axis shows 40 m, hence, displacement at t = 3 s is 40 m
Out of the following, the correct displacement-time graph for uniform motion is:

Answer
The correct displacement-time graph for uniform motion is :

Reason — When the displacement-time graph is a straight line inclined to the time axis, then the body covers equal distances in equal intervals of time and shows uniform motion.
From the velocity-time graph, we can determine :
- The displacement of the body in a certain time interval.
- The acceleration of the body at any instance.
- Both (1) and (2)
- None of these
Answer
Both (1) and (2)
Reason — (1) Since, velocity x time = displacement, the area enclosed between the velocity-time sketch and X-axis (i.e., the time axis) gives the displacement of the body.
(2) Since, acceleration is equal to the ratio of change in velocity and time taken, therefore the slope (or gradient) of the velocity-time sketch gives the acceleration.
The velocity-time graph of a body in motion is a straight line inclined to the time axis. The correct statement is —
- velocity is uniform
- acceleration is uniform
- both velocity and acceleration are uniform
- neither velocity nor acceleration is uniform.
Answer
acceleration is uniform
Reason — When the velocity-time graph of a body in motion is a straight line inclined to the time axis then there are equal changes in velocity in equal intervals of time and hence, the movement is with uniform acceleration.
For a uniformly retarded motion, the velocity-time graph is :
- a curve
- a straight line parallel to the time axis
- a straight line perpendicular to the time axis
- a straight line inclined to the time axis.
Answer
a straight line inclined to the time axis
Reason — If the motion is uniformly retarded (i.e., its velocity decreases by an equal amount in each second), the velocity-time graph will be a straight line inclined to the time axis with a negative slope.
Study the velocity-time graph shown below and answer the questions that follow :

(i) The distance travelled in 5s :
- 10 m
- 50 m
- 125 m
- 250 m
(ii) The retardation of the body as calculated from the graph is :
- 12 ms-2
- 15 ms-2
- 10 ms-2
- 20 ms-2
Answer
(i) 125 m
Reason — Area under the velocity-time graph will give the distance travelled in 5 secs :
Area = x base x height
= x 5 x 50
=
= 125 m
Hence, distance travelled in 5s = 125 m
(ii) 10 ms-2
Reason —
Hence, retardation = 10 ms-2
The graph representing the state of rest of an object is :

Answer
The graph representing the state of rest of an object is :

Reason — As distance is not changing in distance-time graph hence, the state of rest of an object is shown.
Which of the following graphs shown below represents the uniform motion of an object?

Answer
The graph representing the uniform motion of an object is :

Reason — As in velocity-time graph, velocity of the body is not changing, therefore, the body is covering equal distance in equal intervals of time and is in uniform motion.
The velocity-time graph given below shows :

- Uniform acceleration
- Average speed
- Uniform velocity
- All of these
Answer
Uniform velocity
Reason — As in velocity-time graph, velocity of the body is not changing, therefore, the body is covering equal distance in equal intervals of time and is in uniform motion.
In the velocity-time graph shown below, the ratio of the distance travelled by the object in the last 2 s and the distance travelled in 7 s is :

Answer
Reason — Distance covered in last 2 s = area of triangle = x 2 x 10 = 10 m
Distance covered in last 7 s = area of trapezium = x 10 x (2 + 6) = 40 m
Hence, ratio of of the distance travelled by the object in the last 2 s and the distance travelled in 7 s is = =
The velocity-time graph given below shows an object moving in a straight line. The displacement and the distance travelled by the object in 6 s will respectively be :

- 8 m, 16 m
- 16 m, 8 m
- 16 m, 16 m
- 8 m, 8 m
Answer
8 m, 16 m
Reason — Displacement = area of 1st rectangle - area of 2nd rectangle + area of third rectangle
= [4 x 2] - [2 x 2] + [2 x 2] = 8 m
Distance = area of 1st rectangle + area of 2nd rectangle + area of third rectangle
= [4 x 2] + [2 x 2] + [2 x 2] = 16 m
A rubber ball falls freely from a height h onto a smooth floor. After striking the floor, the ball again rises to the same height. Assume that the duration of contact of the ball with the floor is negligible. Identify the correct graph for velocity with time and height with time.
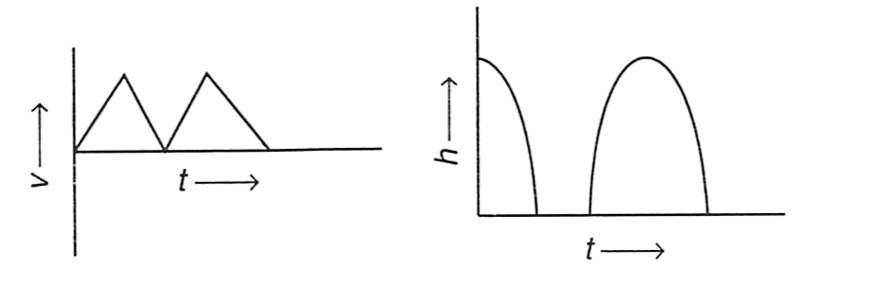
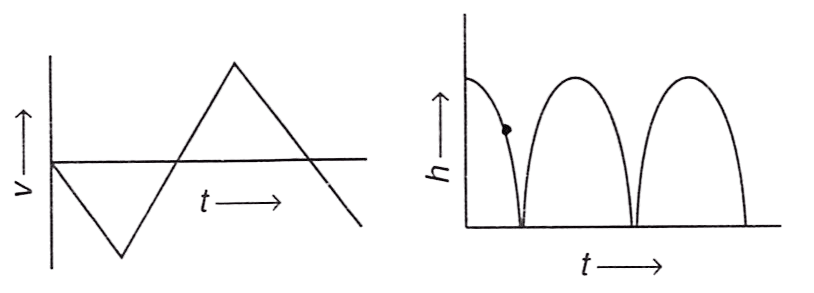
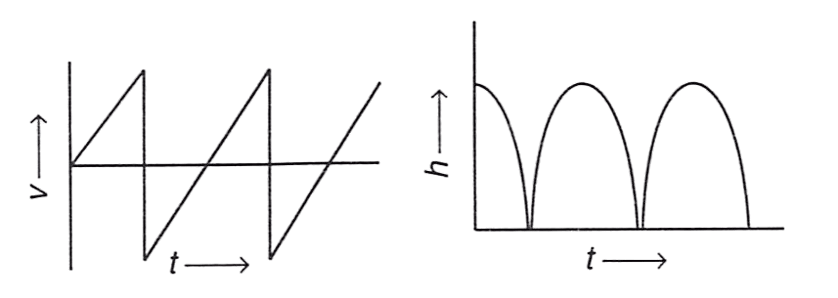
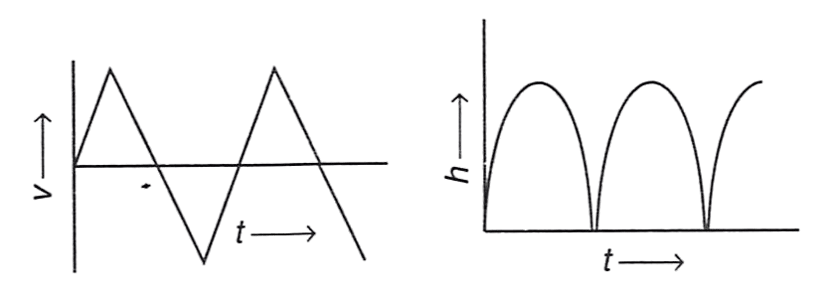
Answer
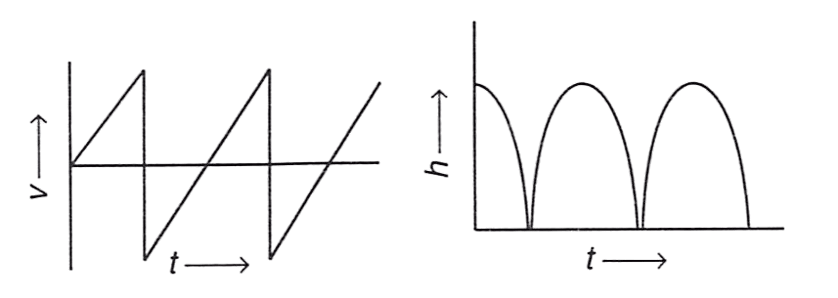
Reason —
Option (1) :
Velocity graph is incorrect as it always shows positive velocity and height graph is also incorrect because it shows that height of ball was zero for some amount of time whereas in the question it is mentioned that ball was in contact with floor for negligible time.
Option (2) :
Velocity graph is incorrect because it's linear sections with sign reversal is not following height-time graph but height graph is correct as it is smooth parabolic curves representing motion to and from height h.
Option (3) :
Velocity graph is correct because it's linear sections with sign reversal is following height-time graph and height-time graph is also correct as it is smooth parabolic curves representing motion to and from height h.
Option (4) :
Velocity graph is incorrect because the process of sign reversal of velocity should be instantaneous and have no time gap during sign reversal. Height graph is also incorrect as it shows the ball has started it's motion from ground (h = 0) which is not the case as the ball is released from a particular height.
For the motion with uniform velocity, how is the distance travelled related to the time?
Answer
For the motion with uniform velocity, distance is directly proportional to time.
What does the slope of a displacement-time graph represent?
Answer
As, velocity is the ratio of displacement and time, therefore, the slope gives the velocity.
When slope is positive, it implies body is moving away from the starting (reference) point.
When slope is negative, it implies body is returning towards the starting (reference) point.
When can the distance-time and displacement-time graph be the same?
Answer
For a motion in one direction in a straight line, since the direction of motion does not change, so displacement-time graph and the distance-time graph are same.
What information do we get by a greater slope of displacement-time graph?
Answer
A greater slope of displacement-time graph shows higher velocity.
What information is conveyed about motion by the negative slope of a displacement-time graph?
Answer
The negative slope of a displacement-time graph shows the motion towards the origin.
What does the slope of velocity-time graph represent?
Answer
As the ratio of change in velocity and time taken is equal to the acceleration. Therefore, the slope of the velocity-time graph represents the acceleration.
What information do we get by a higher slope of velocity-time graph?
Answer
On the velocity-time graph, larger the slope, higher is the acceleration or retardation.
What information do we get about motion by the negative slope of a velocity-time graph?
Answer
If the velocity-time graph has a negative slope, the motion of body decreases at a constant rate (i.e., motion is uniformly retarded).
What informations about the motion of a body are obtained from the displacement-time graph ?
Answer
In a displacement time graph, the time is on the X axis and the displacement of the body is on the Y axis. As, velocity is the ratio of displacement and time, therefore, the slope gives the velocity.
When slope is positive, it implies body is moving away from the starting (reference) point.
When slope is negative, it implies body is returning towards the starting (reference) point.
Can displacement-time sketch be parallel to the displacement axis ? Give reason to your answer.
Answer
No, the displacement-time sketch can never be a straight line, parallel to the displacement axis because such a line would mean that the distance covered by the body in a certain direction increases without any increase in time (i.e., the velocity of the body is infinite) which is impossible.
Draw a displacement-time graph for a boy going to school with a uniform velocity.
Answer
Below is the displacement-time graph for a boy going to school with a uniform velocity :

State how the velocity-time graph can be used to find —
(i) the acceleration of a body,
(ii) the distance travelled by the body in a given time, and
(iii) the displacement of the body in a given time.
Answer
(i) Acceleration of a body — As acceleration is equal to the ratio of change in velocity and time taken, therefore, the slope ( or gradient ) of the velocity-time graph gives the acceleration.
(ii) Distance travelled by the body in a given time — The total distance travelled by the body is obtained by the arithmetic sum of the positive displacement and negative displacement (without sign).
(iii) Displacement of the body — As the product of velocity and time gives the displacement, therefore, the area enclosed between the velocity-time sketch and X - axis (i.e., the time axis) gives the displacement of the body.
The total displacement is obtained by adding positive displacement and negative displacement numerically with proper sign.
What can you say about the nature of motion of a body if its displacement-time graph is —
(a) a straight line parallel to time axis?
(b) a straight line inclined to the time axis with an acute angle?
(c) a straight line inclined to the time axis with an obtuse angle?
(d) a curve
Answer
The following can be said about the nature of motion of a body, if its displacement-time graph is as follows —
(a) A straight line parallel to time axis — shows that the body is stationary (or no motion).
(b) A straight line inclined to the time axis with an acute angle — shows the linear relationship between the displacement and time (i.e., the body travels equal distance in equal intervals of time in a certain direction). Hence, we can say the motion is away from the starting point with uniform velocity.
(c) A straight line inclined to the time axis with an obtuse angle — shows that there is motion towards the starting point with a uniform velocity.
(d) A curve — shows that the body moves with varying speed in a fixed direction. Hence, we can say that there is motion with variable velocity.
The figure shows displacement-time graph of two vehicles A and B moving along a straight road. Which vehicle is moving faster? Give reason.

Answer
We infer from the graph, that vehicle A is moving faster than vehicle B. It is so because, the slope of line A is more than that of line B.
How is the velocity obtained from the displacement-time graph for a body moving with a varying speed in a fixed direction?
Answer
If a body moves with varying speed in a fixed direction i.e., with variable velocity, the displacement-time graph is not a straight line, but it is a curve. The velocity at any instant can then be obtained by finding the slope of the tangent drawn on the curve at that instant of time.
Draw a velocity-time graph for a body moving with an initial velocity u and uniform acceleration a. Use this graph to find the distance travelled by the body in time t.
Answer
Below is the velocity-time graph for a body moving with an initial velocity u and uniform acceleration a:

Let v be the velocity at time t for this body having initial velocity u and uniform acceleration a as shown in the graph.
Distance travelled by the body in time t = Area under the velocity-time curve.
Hence,
Distance travelled = area of trapezium OABD
= x sum of parallel sides x height
= x (OA + DB) x OD
= x (u + v) x t
=
State the type of motion represented by the following sketches in (a) and (b).
Give example of each type of motion.
(a)

(b)

Answer
(a) The graph shows uniformly accelerated motion.
Example — Uniform acceleration is depicted by the motion of a body released downwards.
(b) The graph shows the motion with a variable retardation.
Example — Motion with a variable retardation is shown by a car approaching its destination.
Figure shows the velocity-time graph for two cars A and B moving in same direction. Which car has the greater acceleration? Give reason to your answer.

Answer
We can infer from the graph, that the car B has greater acceleration than car A as the slope of straight line for car B is more than that of car A.
Draw the velocity-time graph for a body moving with —
(a) uniform velocity,
(b) uniform acceleration.
Answer
(a) Below is the velocity-time graph for a body moving with uniform velocity :

(b) Below is the velocity-time graph for a body moving with uniform acceleration :

The velocity-time graph for a uniformly retarded body is a straight line inclined to the time axis with an obtuse angle. How is retardation calculated from the velocity-time graph?
Answer
Retardation is calculated from the velocity-time graph, by finding the negative slope.
The figure given below shows the displacement-time graph for four bodies A, B, C and D. In each case state what information do you get about the acceleration (zero, positive or negative).

Answer
The following information is obtained from the given figures —
- A → Zero acceleration since slope (i.e., velocity) is constant.
- B → Zero acceleration since slope (i.e., velocity) is constant.
- C → Negative acceleration (or retardation) since slope is decreasing with time.
- D → positive acceleration since slope is increasing with time.
Draw a graph for acceleration against time for a uniformly accelerated motion. How can it be used to find the change in speed in a certain interval of time?
Answer
Below is the graph for acceleration against time for a uniformly accelerated motion:

For linear motion,
Acceleration x time = change in speed
Therefore, we can find the change in speed from the area enclosed between the acceleration-time sketch and the time axis.
Draw a velocity-time graph for the free fall of a body under gravity, starting from rest.
Take g = 10 m s-2.
Answer
Below is the velocity-time graph for the free fall of a body under gravity, starting from rest :

How is the distance related with time for the motion under uniform acceleration such as the motion of a freely falling body ?
Answer
For a freely falling body (i.e., motion under uniform acceleration ), the displacement is directly proportional to the square of time.
S ∝ t2
A body falls freely from a certain height. Show graphically the relation between the distance fallen and square of time. How will you determine g from this graph?
Answer
Below is the graph of distance fallen against square of time for a freely falling body :

The slope is half the acceleration due to gravity.
Thus, the value of acceleration due to gravity (g) can be obtained by doubling the slope of the S - t2 graph for a freely falling body.
Draw the velocity-time graph for a body moving with —
(a) uniform velocity,
(b) uniform acceleration.
and give one example of each and also calculate the displacement and acceleration.
Answer
(a) Below is the velocity-time graph for a body moving with uniform velocity :

Example : In the fig. given below, a straight line AB, represents the velocity-time graph of a body moving with a uniform velocity 4 ms-1 for 5 s.

Displacement in 5 second = area of rectangle OABC = OC x OA = 5 x 4 = 20 m
Hence, displacement = 20m
The slope of the straight line AB is zero, therefore, its acceleration is zero.
(b) Below is the velocity-time graph for a body moving with uniform acceleration :

Example : The table below represents the velocity of a body at different instants, starting from rest.
| Time (s) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Displacement (m) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |

Distance travelled in 8 s = S = area of triangle OPQ
= x base x height = x OQ x QP = x 8 x 80 = 320 m
Acceleration of body = slope of line OP
= = = 10 ms-2
Hence, distance covered is 320 m and acceleration = 10 ms-2
Draw the acceleration-time graph for a body moving with :
(a) Uniform velocity
(b) Free falling body
and give an example of each.
Answer
(a) Below is the acceleration-time graph for a body moving with uniform velocity :

In the above figure, if the body is moving with a uniform velocity, the acceleration is zero. Hence, acceleration-time graph in such a case is a straight line coinciding with time axis.
An example of a body moving with uniform velocity is a car travelling on a straight and flat road with a constant speed of 60 km/hour (or any other constant speed).
(b) Below is the acceleration-time graph for a free falling body :

In the figure given above, the straight line AF, represents the acceleration-time graph for a body falling freely with uniform acceleration of 10 ms-2.
For example, a body falling freely under gravity moves with a uniform acceleration of 9.8 ms-2 (or nearly 10 ms-2).
Figure (a) shows the displacement-time graph for the motion of a body. Use it to calculate the velocity of body at t = 1 s, 2 s and 3 s, then draw the velocity-time graph for it in Figure (b).

Answer

We observe from the given displacement-time graph above, that the slope is a straight line inclined with time axis, so the body is moving with uniform velocity. Hence, the velocity will be same at t = 1 s, 2 s and 3 s.
Hence, velocity at t = 1 s, 2 s and 3 s is equal to 2 m s-1
Velocity-time graph for the motion of a body is given below :

Following table gives the displacement of a car at different instants of time.
| Time (s) | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Displacement (m) | 0 | 5 | 10 | 15 | 20 |
(a) Draw the displacement-time sketch and find the average velocity of car.
(b) What will be the displacement of car at (i) 2.5 s and (ii) 4.5 s ?
Answer
(a) The displacement-time sketch for the car is shown below :

As we know,
Hence, average velocity of the car is 5 ms-1.
(b) When we observe the graph, we can find the displacement of the car at various points,
At t = 2.5 s, displacement = 12.5 m and
At t = 4.5 s, displacement = 22.5 m
A body is moving in a straight line and its displacement at various instants of time is given in the following table —
| Time (s) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| Displacement (m) | 2 | 6 | 12 | 12 | 12 | 18 | 22 | 24 |
Plot displacement-time graph and calculate —
(i) Total distance travelled in interval 1 s to 5 s,
(ii) Average velocity in time interval 1 s to 5 s.
Answer
The displacement-time graph is given below :

(i) When we observe the graph, we find —
Total distance travelled in interval 1 s to 5 s = 18 m - 6 m = 12 m
Hence, total distance travelled in interval 1 s to 5 s = 12 m
(ii) As we know,
Hence, average velocity of the car in interval 1 s to 5 s is 3 ms-1.
Figure shows the displacement of a body at different times.

(a) Calculate the velocity of the body as it moves for time interval
(i) 0 to 5 s,
(ii) 5 s to 7 s and
(iii) 7 s to 9 s.
(b) Calculate the average velocity during the time interval 5 s to 9 s.
[ Hint — From 5 s to 9 s, displacement = 7 m - 3 m = 4 m ]
Answer
Below is the displacement-time graph of the body with the different points marked :

(a) As we know,
(i) At t = 0 to 5 s
Velocity = Slope of straight line OA
Hence, velocity at t = 0 to 5 s = 0.6 m s-1
(ii) At t = 5 to 7 s
In this part we observe that there is no change in Y axis, (i.e. displacement is zero so the body is stationary).
Hence, velocity at t = 5 to 7 s = 0 m s-1
(iii) At t = 7 s to 9 s
Velocity = Slope of straight line BC
Hence, velocity at t = 7 s to 9 s = 2 m s-1
(b) As we know,
Substituting the values from the graph we get,
Hence, average velocity of the car is 1 ms-1.
From the displacement-time graph of a cyclist, given in figure, find —
(i) The average velocity in the first 4 s,
(ii) The displacement from the initial position at the end of 10 s
(iii) The time after which he reaches the starting point.

Answer
(i) As we know,
Substituting the values from the graph, for the first 4 s, we get,
Hence, average velocity of the car is 2.5 ms-1.
(ii) From the graph, we get,
Displacement = final position - initial position
Substituting the values from the graph, for the first 10 s, we get,
Displacement = -10 - 0 = -10 m
Hence, displacement from the initial position at the end of 10 s = - 10 m
(iii) The cyclist would reach the start point two times, one at the 7 s and the other at 13 s.
Figure ahead represents the displacement-time sketch of motion of two cars A and B.

Find —
(i) The distance by which the car B was initially ahead of car A.
(ii) The velocities of car A and car B
(iii) The time in which car A catches car B
(iv) The distance from start when the car A will catch the car B
Answer
(i) When we observe the graph, we find that the car B was ahead of car A by 40 km.
(ii) As we know,
Cars A and B have uniform velocities as displacement-time graph for both are straight lines.
At t = 4 h
Car A
Hence, velocity of car A = 40 km h-1
Car B
Hence, velocity of car B = 20 km h-1
When we observe the graph, we find that both cars A and B intersect at a point K.
Hence,
(iii) the car A catches car B at time (t) = 2 h.
(iv) the distance from start when the car A will catch the car B = 80 km.
A body at rest is made to fall from the top of a tower. Its displacement at different instants is given in the following table —
| Time (in s) | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
|---|---|---|---|---|---|---|
| Displacement (in m) | 0.05 | 0.20 | 0.45 | 0.80 | 1.25 | 1.80 |
Draw a displacement-time graph and state whether the motion is uniform or non-uniform?
Answer
Below is the displacement-time graph of the body made to fall from the top of a tower:

When we observe the graph, we find, that the displacement-time graph is a curve.
Hence, we can say that the motion is non-uniform.
Figure shows the velocity-time graph for the motion of a body. Use it to find the displacement of the body at t = 1 s, 2 s, 3 s and 4 s, then draw the displacement-time graph for it on figure (b).

Answer
As we know, the displacement of body at any instant can be obtained by finding the area enclosed by the straight line with the time axis up to that instant.
Let displacements at t = 1 s, 2 s, 3 s, 4 s be S1, S2, S3, S4 respectively.
At t = 1 s,
S1 = x 1 x 1 = 0.5 m
At t = 2 s,
S2 = x 2 x 2 = 2 m
At t = 3 s,
S3 = x 3 x 3 = 4.5 m
At t = 4 s,
S4 = x 4 x 4 = 8 m
The table below gives the displacement of body at different instants.
| Time (in s) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Displacement (in m) | 0.5 | 2 | 4.5 | 8 |
The displacement time graph is shown below :

Figure below shows a velocity-time graph for a car starting from rest. The graph has three parts AB, BC and CD.
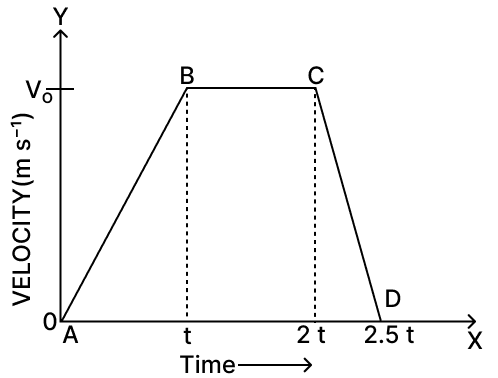
(i) State how is the distance travelled in any part determined from this graph.
(ii) Compare the distance travelled in part BC with the distance travelled in part AB.
(iii) Which part of graph shows motion with uniform (a) velocity (b) acceleration (c) retardation?
(iv) (a) Is the magnitude of acceleration higher or lower than that of retardation? Give a reason. (b) Compare the magnitude of acceleration and retardation.
Answer
(i) The distance travelled in any part of the graph can be obtained by finding the area enclosed by the graph in that part with the time axis.
(ii) Let E be the point on time axis (x axis) at time t and F be the point at time 2t.
When we observe the graph, we find,
Distance travelled in part BC = Area of rectangle EBCF
∴ Distance travelled in part BC = length x breadth
= (2t - t) x (v0 - 0)
= t x v0 .... [1]
Distance travelled in part AB = Area of triangle ABT
∴ Distance travelled in part AB = x base x height
= x (t - 0) x (v0 - 0)
= x t x v0 .... [2]
Comparing [1] and [2] we get,
Distance travelled in part BC : Distance travelled in part AB
Hence,
Distance travelled in part BC : Distance travelled in part AB = 2 : 1
(iii) The different parts of the graph are mentioned below:
(a) Uniform velocity is shown in part BC of the graph, as the velocity is constant with time.
(b) Uniform acceleration is shown in part AB of the graph, as the velocity is increasing with time.
(c) Uniform retardation is shown in part CD of the graph, as the velocity is decreasing with time.
(iv) (a) The magnitude of acceleration is lower, as slope of line AB is less than that of line CD.
(b) Acceleration in part AB = slope of AB
Retardation in part CD = slope of CD
Magnitude of acceleration : Magnitude of retardation = Slope of line AB : Slope of line CD
Hence, Magnitude of acceleration : Magnitude of retardation = 1 : 2
The velocity-time graph of a moving body is given below in figure
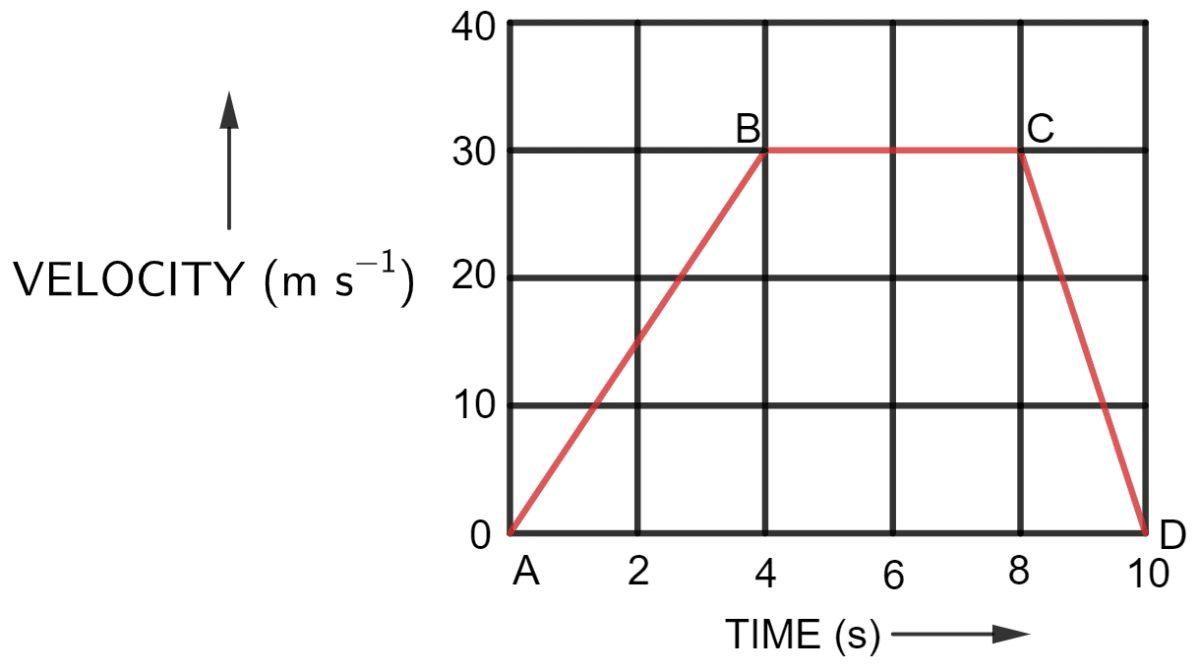
Find —
(i) The acceleration in parts AB, BC and CD.
(ii) Displacement in each part AB, BC, CD, and
(iii) Total displacement.
Answer
Let E be the point at t = 4 and F be the point at t = 8 as labelled in the graph below :
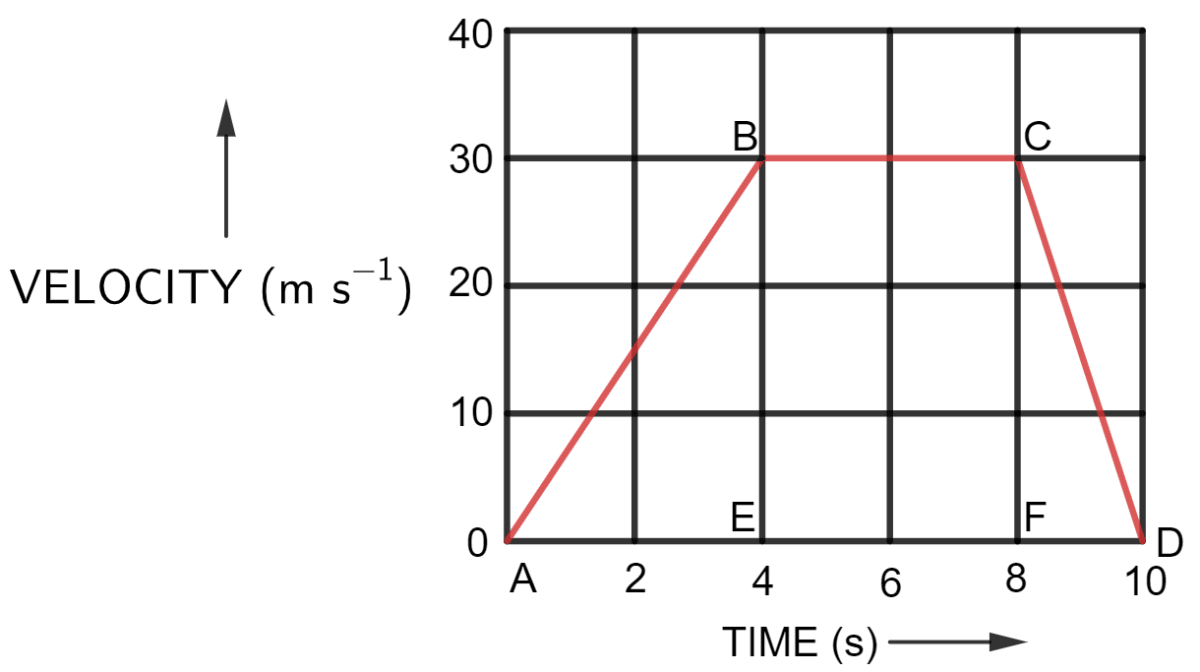
(i) Acceleration in part AB = slope of AB
Hence, Acceleration in part AB = 7.5 m s-2
Acceleration in part BC = slope of BC
We observe from the graph that there is no change in velocity in part BC. Hence, Acceleration in part BC = 0 m s-1
Acceleration in part CD = slope of CD
Hence, Acceleration in part CD = -15 m s-1
(ii) Displacement in each part is as follows —
(a) Displacement of part AB = Area of triangle ABE
Substituting the values in the formula above, we get,
Hence,
Displacement of part AB = 60 m
(b) Displacement of part BC = Area of Square EBCF
Substituting the values in the formula above, we get,
Hence,
Displacement of part BC = 120 m
(c) Displacement of part CD = Area of triangle CDF
Substituting the values in the formula above, we get,
Hence,
Displacement of part CD = 30 m
(iii) Total displacement = Displacement of part AB + Displacement of part BC + Displacement of part CD
= 60 + 30 + 120 = 210
Hence,
total displacement = 210 m
A ball moves on a smooth floor in a straight line with a uniform velocity 10 m s-1 for 6 s. At t = 6 s, the ball hits a wall and comes back along the same line to the starting point with same speed. Draw the velocity-time graph and use it to find the total distance travelled by the ball and its displacement.
Answer
The velocity-time graph for the motion of ball on a smooth floor in a straight line is shown below :

Total distance travelled = distance travelled in the first 6 s + distance travelled in next 6 s.
As we know,
Distance = velocity x time
Substituting the values in the formula above we get,
Distance when the ball moves towards the wall = 10 m s-1 x 6 s = 60 m
Distance when the ball moves away from the wall = 10 m s-1 x 6 s = 60 m
Total distance = 60 m + 60 m = 120 m
Displacement = distance travelled in the forward direction - distance travelled while coming back
= 60 m - 60 m = 0
∴ Displacement = 0 as the ball comes back to the initial place.
Figure shows the velocity-time graph of a particle moving in a straight line.

(i) State the nature of motion of particle.
(ii) Find the displacement of particle at t = 6 s.
(iii) Does the particle change its direction of motion?
(iv) Compare the distance travelled by the particle from 0 to 4 s and from 4 s to 6 s.
(v) Find the acceleration from 0 to 4 s and retardation from 4 s to 6 s.
Answer
(i) As we observe the graph, we find that, the nature of motion of particle is that, the particles are uniformly accelerated from 0 to 4s and then uniformly retarded from 4s to 6s.
(ii) As we know,
displacement of particles can be obtained by finding the area enclosed by the graph in that part with the time axis up to that instance.
At t = 6 s,
Displacement = area of triangle
Substituting the values in the formula above, we get,
Hence,
Displacement of particle at t = 6 s is 6 m
(iii) No, the particle does not change its direction of motion.
(iv) At t = 0 to 4 s,
Distance covered = area of triangle
Substituting the values in the formula above, we get,
Hence,
Distance covered between 0 to 4 s = 4 m
At t = 4 s to 6 s,
Distance covered = area of triangle
Substituting the values in the formula above, we get,
Hence,
Distance covered between 4s to 6 s = 2 m
∴ Distance covered between 0 to 4 s : Distance covered between 4 s to 6 s = 4 : 2 = 2 : 1
(v) Acceleration in part 0 s to 4 s = slope of graph
Hence,
Acceleration in part 0 s to 4 s = 0.5 m s-2
As we know,
Retardation in part 4 s to 6 s = slope of graph
Acceleration = -1 ms-2 and as we know retardation is negative acceleration
Hence, Retardation in part 4 s to 6 s = 1 m s-2
When a body starts from rest, the equation of motion takes the form :
- v = u
- v = at
- v = at2
- S = ut + at2
Answer
v = at
Reason — When a body starts from rest, initial velocity is zero (u = 0), then v = at.
If a body is moving with a uniform retardation, then its acceleration will be :
- Positive
- Negative
- Zero
- Cannot say
Answer
Negative
Reason — When a body is moving with uniform retardation, then acceleration will be negative.
A car acquires a velocity of 54 ms-1 in 20 s starting from rest, then its acceleration is :
- 5.4 ms-2
- 2.7 ms-2
- 7.2 ms-2
- 2.0 ms-2
Answer
2.7 ms-2
Reason — Given,
u = 0
v = 54 ms-1
t = 20 s
a = ?
Using, v = u + at or
a =
a = = 2.7 ms-2 .
Hence, acceleration = 2.7 ms-2
A particle starts to move in a straight line from a point with a velocity 10 ms-1 and acceleration -2.0 ms-2. Its position at t = 5 s will be :
- 5 m
- 10 m
- 20 m
- 25 m
Answer
25 m
Reason — Given,
u = 10 ms-1
a = -2.0 ms-2
t = 5 s
Using, S = ut + at2
S = (10 x 5) + x (-2) x 52 = [50 - 25] = 25 m
Hence, its position at t = 5 s will be 25 m
A body initially at rest, starts moving with a constant acceleration of 0.5 ms-2 and travels a distance 25 m, then its final velocity is :
- 5 ms-1
- 20 ms-1
- 15 ms-1
- -15 ms-1
Answer
5 ms-1
Reason — Given,
u = 0
a = 0.5 ms-2
S = 25 m
v = ?
Using, v2 = u2 + 2aS
v2 = 0 + [2 x 0.5 x 25] = 25
Hence, v = 5 ms-1
A car starting from rest accelerates uniformly to acquire a speed 20 km h-1 in 30 min. The distance travelled by car in this time interval will be —
- 600 km
- 5 km
- 6 km
- 10 km
Answer
5 km
Reason —
As we know,
v = u + at
Given,
u = 0
v = 20 km h-1
t = 30 min = h
Substituting the values in the formula above, we get,
Now,
S = ut + at2
Substituting the values in the formula above we get,
Hence, distance = 5 km
A car starting from rest moves on a straight path for time t = 0 to t = T with a uniform acceleration a and then stops with a uniform retardation. The average speed of the car will be :
aT
Answer
Reason
Assuming, uniform retardation has the same value as the uniform acceleration (a).
Case 1 : When car is accelerating
Given,
Initial speed (u1) = 0
Acceleration (a1) = a
Time (t1) = T
Let, distance travelled be S1 and final velocity is v1.
As,
v = u + at
On putting values
v1 = u1 + a1t1 = 0 + aT = aT
By using,
S = ut + at2
On putting values
S1 = u1t1 + a1 = 0 + aT2 = aT2
Case 2 : When car is retarding
Given,
Initial speed (u2) = v1 = aT
Acceleration (a2) = -a
Final speed (v2) = 0
Let, distance travelled be S2 and time taken is t2.
As,
v = u + at
On putting values
v2 = u2 + a2t2
⟹ 0 = aT - at2
⟹ aT = at2
⟹ t2 = T
By using,
S = ut + at2
On putting values
S2 = u2t2 + a2
= (aT)(T) - aT2
= aT2 - aT2
= aT2
Here,
Total distance travelled (S) = S1 + S2 = aT2 + aT2 = aT2
Total time taken (t) = t1 + t2 = T + T = 2T
Then,
∴ Average speed of the car is
Assertion (A) : The displacement of a body can be zero even if the distance travelled by it is not zero.
Reason (R) : Displacement is the shortest distance from the initial to the final position of body.
- both A and R are true and R is the correct explanation of A
- both A and R are true and R is not the correct explanation of A
- assertion is false but reason is true
- assertion is true but reason is false
Answer
both A and R are true and R is the correct explanation of A
Explanation
Assertion (A) is true because if a body moves and comes back to its starting point (e.g., in a circular path or a round trip), the displacement is zero because the initial and final positions are the same, but the distance travelled is not zero.
Reason (R) is true because by definition, displacement is the shortest straight line distance between the initial and final positions of the body. So, the reason correctly explains the assertion.
Assertion (A) : For a given time interval, average velocity and average speed can have different values.
Reason (R) : Speed is a scalar quantity whereas velocity is a vector quantity.
- both A and R are true and R is the correct explanation of A
- both A and R are true and R is not the correct explanation of A
- assertion is false but reason is true
- assertion is true but reason is false
Answer
both A and R are true and R is the correct explanation of A
Explanation
Assertion (A) is true because :
and
So if the path is not straight (e.g., in a circular or zig-zag path), distance > displacement, so average speed > average velocity in such cases.
Reason (R) is true because speed has only magnitude (no direction) i.e., scalar and velocity has both magnitude and direction i.e., vector. Hence, the reason correctly explains why average speed and average velocity can differ because velocity depends on displacement (vector) and speed depends on distance (scalar).
Assertion (A) : The slope of displacement-time graph gives the velocity.
Reason (R) : Velocity is the product of displacement and time.
- both A and R are true and R is the correct explanation of A
- both A and R are true and R is not the correct explanation of A
- assertion is false but reason is true
- assertion is true but reason is false
Answer
assertion is true but reason is false
Explanation
Assertion (A) is true because the slope of a displacement-time graph is :
Reason (R) is false because velocity is not the product of displacement and time.
Instead,
Assertion (A) : The velocity-time graph of a body in motion can be a straight line parallel to the time axis.
Reason (R) : This is because the motion of body is with uniform velocity.
- both A and R are true and R is the correct explanation of A
- both A and R are true and R is not the correct explanation of A
- assertion is false but reason is true
- assertion is true but reason is false
Answer
both A and R are true and R is the correct explanation of A
Explanation
There is a misprint in the question, velocity axis should be printed as time axis.
Assertion (A) is true because a straight line parallel to the time (x) axis implies same velocity for at all times so this happens when the velocity remains constant over time, i.e., uniform velocity.
Reason (R) is true because a horizontal velocity-time graph (parallel to the time axis) indicates uniform velocity which shows the velocity doesn’t change with time and hence, Reason justifies the assertion.
Assertion (A) : The acceleration-time graph of а body is a straight line parallel to time axis.
Reason (R) : This depicts the motion of freely falling body under gravity.
- both A and R are true and R is the correct explanation of A
- both A and R are true and R is not the correct explanation of A
- assertion is false but reason is true
- assertion is true but reason is false
Answer
both A and R are true and R is the correct explanation of A
Explanation
Assertion (A) is true because if a body moves with constant acceleration, the acceleration-time graph is indeed a straight horizontal line parallel to the time axis.
Reason (R) is true because for a freely falling body under gravity (ignoring air resistance), the acceleration is constant and equal to g (= 9.8 m/s²) and this produces a horizontal acceleration-time graph so the reason correctly explains the assertion.
Assertion (A) : Acceleration of a moving body is always positive.
Reason (R) : Acceleration is the rate of change of velocity with time.
- both A and R are true and R is the correct explanation of A
- both A and R are true and R is not the correct explanation of A
- assertion is false but reason is true
- assertion is true but reason is false
Answer
assertion is false but reason is true
Explanation
Assertion (A) is false because acceleration can be positive, negative (retardation), or zero depending on whether the velocity is increasing, decreasing, or constant.
Reason (R) is true because acceleration of a body is given by :
Write three equations of uniformly accelerated motion relating the initial velocity (u), final velocity (v), time (t), acceleration (a) and displacement (S).
Answer
The equations of uniformly accelerated motion relating to the initial velocity (u), final velocity (v), time (t), acceleration (a) and displacement (S) are as follows —
(i) v = u + at
(ii) S = ut + at2
(iii) v2 = u2 + 2aS
Write an expression for the distance S covered in time t by a body which is initially at rest and starts moving with a constant acceleration a.
Answer
According to equation of motion —
S = ut + at2
Where,
S = distance covered
u = initial velocity
a = acceleration
t = time
As, body is at rest, so u = 0
Hence, we get,
Hence, we get,
S = at2
Derive the following equations for a uniformly accelerated motion —
(i) v = u + at
(ii) S = ut + at2
(iii) v2 = u2 + 2aS
where the symbols have their usual meanings.
Answer
(i) By definition,
Hence,
Hence, we get,
v = u + at [Eq. 1]
(ii) By definition,
or
But, from Eq. 1, v = u + at
Therefore,
Hence, we get,
S = ut + at2
(iii) By definition,
But, from Eq. 1, v = u + at
or t =
Therefore,
So, v2 - u2 = 2aS
Hence,
v2 = u2 + 2aS
A body starts from rest with a uniform acceleration of 2 m s-2. Find the distance covered by the body in 2 s.
Answer
According to equation of motion —
S = ut + at2
Where,
distance covered = S
initial velocity u = 0
acceleration a = 2 m s-2
time t = 2 s
Substituting the values in the formula for u = 0 , we get,
Hence, distance covered = 4 m
A body starts with an initial velocity of 10 m s-1 and acceleration 5 m s-2. Find the distance covered by it in 5 s .
Answer
According to equation of motion —
S = ut + at2
Where,
distance covered = S
initial velocity u = 10 m s-1
acceleration a = 5 m s-2
time t = 5 s
Substituting the values in the formula, we get,
Hence, distance covered = 112.5 m.
A vehicle is accelerating on a straight road. Its velocity at any instant is 30 km h-1, after 2 s, it is 33.6 km h-1 and after further 2 s, it is 37.2 km h-1. Find the acceleration of vehicle in m s-2. Is the acceleration uniform ?
Answer
As we know,
a =
After t = 2s,
u = 30 km h-1
Converting km h-1 to m s-1
We get,
Hence, 30 km h-1 is equal to 8.33 m s-1.
Now,
v = 33.6 km h-1
Converting km h-1 to m s-1
We get,
Hence, 33.6 km h-1 is equal to 9.33 ms-1.
Substituting the values in the formula above, we get,
Hence, acceleration in the first 2 s = 0.5 m s -2
For the next 2 s,
u = 9.33 m s-1
v = 37.2 km h-1
Converting km h-1 to m s-1
We get,
Hence, 37.2 km h-1 is equal to 10.33 ms-1.
Substituting the values in the formula above, we get,
Hence, acceleration is 0.5 m s -2
Yes, the acceleration is uniform as the acceleration in both instances is same.
A body, initially at rest, starts moving with a constant acceleration 2 m s -2.
Calculate —
(i) the velocity acquired and
(ii) and the distance travelled in 5 s.
Answer
As we know, from the equation of motion,
v = u + at
Given,
a = 2 m s -2
u = 0
t = 5 s
Substituting the values in the formula, we get,
Hence, the velocity acquired = 10 m s-1
(ii) According to equation of motion —
S = ut + at2
Substituting the values in the formula, we get,
Hence, distance travelled = 25 m
A bullet initially moving with a velocity 20 m s-1 strikes a target and comes to rest after penetrating a distance 10 cm in the target. Calculate the retardation caused by the target.
Answer
According to equation of motion —
v2 = u2 + 2aS
Given,
u = 20 m s-1,
v = 0,
s = 10 cm = 0.1 m
Substituting the values in the formula above, we get,
Hence, Retardation is 2000 m s-2
A train moving with a velocity of 20 m s-1 is brought to rest by applying brakes in 5 s. Calculate the retardation.
Answer
According to equation of motion —
v = u + at
Given,
u = 20 m s-1,
v = 0,
t = 5 s
Substituting the values in the formula above, we get,
Hence, Retardation is 4 m s-2
A train travels with a speed of 60 km h-1 from station A to station B and then comes back with a speed 80 km h-1 from station B to station A.
Find —
(i) the average speed, and
(ii) the average velocity of train.
Answer
As we know,
Avg Speed =
Given,
From, A to B
speedAB = 60 km h-1
distance travelled = dAB = d
time taken =
From, B to A
speedBA = 80 km h-1
distance travelled = dBA = d
time taken =
Total distance travelled = d + d = 2d [Eqn. 1]
Total time = + [Eqn. 2]
Substituting the values from the equations 1 and 2 in the formula we get,
Hence, Avg Speed = 68.57 km h-1
(ii) We know,
Average velocity =
As the train starts from station A and comes back to same station, hence, displacement is zero.
Therefore, the average velocity is also zero.
A train is moving with a velocity of 90 km h-1. It is brought to stop by applying the brakes which produce a retardation of 0.5 m s-2.
Find —
(i) the velocity after 10 s, and
(ii) the time taken by the train to come to rest.
Answer
(i) As we know, according to the equation of motion,
v = u + at
Given,
u = 90 km h-1
velocity in m s-1
Hence, 90 km h-1 is equal to 25 m s-1.
v = 0 (as the train stops on application of brakes)
t = 10 s
retardation = -a = -0.5 m s-2
Substituting the values in the formula above we get,
Hence, the velocity after 10 s = 20 m s-1.
(ii) As we know, according to the equation of motion,
v = u + at
Substituting the values in the formula above, to get the time taken by the train to come to rest.
Hence, the time taken by the train to come to rest = 50 s.
A car travels a distance 100 m with a constant acceleration and average velocity of 20 m s-1. The final velocity acquired by the car is 25 m s-1.
Find:
(i) the initial velocity and
(ii) acceleration of car.
Answer
(i) Given,
v = 25 m s-1
As we know,
average velocity = = 20 m s-1
Substituting the value we get,
Hence, initial velocity of the car is 15 m s-1
(ii) We know, from the equation,
v2 = u2 + 2aS
S = 100 m
v = 25 m s-1
u = 15 m s-1
Substituting the values in the formula above we get,
Hence, acceleration of car = 2 m s-2
When brakes are applied to a bus, the retardation produced is 25 cm s-2 and the bus takes 20 s to stop.
Calculate —
(i) the initial velocity of bus, and
(ii) the distance travelled by bus during this time.
Answer
As we know,
v = u + at
Given,
Retardation = -a = -25 cm s-2
Expressing it in m s-2
25 cm s-2 = m s-2
Hence, -a = -0.25 m s-2
t = 20 s
v = 0
u = ?
Substituting the values in the formula above we get,
Hence, the initial velocity of bus = 5 m s-1
(ii) As we know, from the equation of motion,
v2 = u2 + 2aS
Substituting the values, we get,
Hence, distance travelled = 50 m
A body moves from rest with a uniform acceleration and travels 270 m in 3 s. Find the velocity of the body at 10 s after the start.
Answer
As we know,
S = ut + at2
Given,
u = 0 m s -1
S = 270 m
t = 3 s
Substituting the values in the formula above we get,
Hence, a = 60 m s-2
To find out velocity after t = 10 s.
v = u + at
Substituting the values in the formula above we get,
Hence, velocity after 10 s = 600 m s-1
A body moving with a constant acceleration travels the distances 3 m and 8 m respectively in 1 s and 2 s.
Calculate —
(i) the initial velocity, and
(ii) the acceleration of body.
Answer
As we know,
S = ut + at2
Let,
S1 = 3 m
t1 = 1 s
S2 = 8 m
t2 = 2 s
Substituting the values in the formula above we get,
For 8m distance,
Solving Equations 1 & 2,
a = 6 - 2u [Eqn. 1]
a = 4 - u [Eqn. 2]
we get,
0 = 2 - u
⇒ u = 2
Hence, initial velocity = 2 m s -1
Putting the value of u in Equation 2 and solving for a:
Hence, the acceleration of body is 2 m s-2
A car travels with a uniform velocity of 25 m s-1 for 5 s. The brakes are then applied and the car is uniformly retarded and comes to rest in further 10 s.
Find —
(i) the distance which the car travels before the brakes are applied,
(ii) the retardation and
(iii) the distance travelled by the car after applying the brakes.
Answer
(i) As we know,
Distance = Speed x time
Initial velocity = u = 25 m s-1
Final velocity = 0
time = 5 s
Substituting the values in the formula above we get,
Hence, distance covered = 125 m.
(ii) Retardation = -a =
t = 10 s
Substituting the values in the formula above we get,
Hence, retardation of the car = 2.5 m s-2
(iii) As we know,
v2 - u2 = 2aS
Substituting the values in the formula above we get,
Hence, the distance travelled by the car after applying the brakes = 125 m.
A space craft flying in a straight course with a velocity of 75 km s-1 fires its rocket motors for 6.0 s. At the end of this time, its speed is 120 km s-1 in the same direction.
Find —
(i) the space craft’s average acceleration while the motors were firing
(ii) the distance travelled by the space craft in the first 10 s after the rocket motors were started, the motors having been in action for only 6.0 s.
Answer
(i) As we know,
v - u = at
Given,
u = 75 km s-1
v = 120 km s-1
t = 6 s
Substituting the values in the formula above we get,
Hence, acceleration = 7.5 km s-2
(ii) As we know,
S = ut + at2
For the first 6 s,
u = 75 km s-1
a = 7.5 km s-2
Hence, S1 = 585 km
For the next 4 s
S2 = speed x time
Given,
t = 4 s
speed = 120 km s -1
Substituting the values in the formula above, we get,
Hence, S2 = 480 km
Total distance covered by the aircraft = S1 + S2
= 585 + 480
= 1065 km
Hence,
Total distance covered by the aircraft = 1065 km.
A train starts from rest and accelerates uniformly at a rate of 2 m s-2 for 10 s. It then maintains a constant speed for 200 s. The brakes are then applied and the train is uniformly retarded and comes to rest in 50 s.
Find —
(i) the maximum velocity reached,
(ii) the retardation in the last 50 s,
(iii) the total distance travelled, and
(iv)the average velocity of the train.
Answer
As we know,
v = u + at
Given,
u = 0
t = 10 s
a = 2 m s-2
Substituting the values in the formula above we get,
Hence, final velocity = 20 m s-1
(ii) Retardation in last 50 s,
As we know,
v = u + at
Given,
u = 20 m s-1
v = 0 m s-1
t = 50 s
Substituting the values in the formula above we get,
Hence, retardation in the last 50 s = 0.4 m s-2
(iii) As we know,
S = ut + at2
For the first 10 s,
u = 0
a = 2 ms-2
Hence, S1 = 100 m .... [1]
For the next 200 s,
S2 = speed x time
where speed = 20
time = 200 s
Substituting the values in the formula above we get,
Hence, S2 = 4000 m .... [2]
For the next 50 s
Hence, S3 = 500 m .... [3]
So,
Total distance = sum of [1], [2] and [3]
Hence, total distance covered = 4600 m
(iv) average velocity =
Substituting the values in the formula above we get,
Hence, average velocity = 17.69 m s-1