Pressure in Fluids and Atmospheric Pressure

Exercise 4(A) — Multiple Choice Type

Question 1

The force acting normally on a surface is called :

1. pressure
2. friction
3. thrust
4. none of these

Answer

thrust

Reason — When a force is applied in a direction normal (or perpendicular) to the surface, it is called thrust.

Question 2

The thrust exerted by a body placed on a surface is :

1. less than the weight of the body
2. more than the weight of the body
3. equal to the weight of the body
4. independent of the weight of the body.

Answer

equal to the weight of the body

Reason — The thrust exerted by a body placed on a surface is equal to its weight. Thrust is a vector quantity.

Question 3

The S.I. unit of thrust is :

1. dyne
2. ms^-1
3. Newton
4. Nm^-1

Answer

Newton

Reason — S.I. unit of thrust is newton (N) and C.G.S. unit of thrust is dyne, where 1 N = 10⁵ dyne.

Question 4

The effect of a given thrust is:

1. less on large area, more on small area
2. more on large area, small on small area
3. does not depend on area
4. maximum when it is inclined at 45° with the area

Answer

less on large area, more on small area

Reason — The effect of thrust on a surface depends on the area of the surface on which it acts. The effect of a thrust is less on a large area, while it is more on a small area.

Question 5

The pressure exerted on a surface depends on :

1. the nature of the surface on which the thrust is applied
2. the area on which the thrust is applied
3. the magnitude of the thrust applied
4. both (b) and (c)

Answer

both (b) and (c)

Reason — The pressure exerted on a surface depends on two factors :

1. the area on which the thrust is applied and
2. magnitude of thrust.

Question 6

Pressure and thrust are :

1. vector quantities
2. scalar quantities
3. scalar and vector quantities respectively
4. vector and scalar quantities respectively

Answer

scalar and vector quantities respectively

Reason — Pressure is a scalar quantity whereas thrust is a vector quantity, because pressure is defined in terms of magnitude only, and thrust is defined in terms of both magnitude and direction.

Question 7

The S.I. unit of pressure is:

1. N cm^-2
2. Pa
3. N
4. N m²

Answer

Pa

Reason — The S.I. unit of thrust is newton and that of area is metre², so the S.I. unit of pressure is newton per metre² which is abbreviated as N m^-2. This unit is named pascal (Pa) after the name of the french scientist Blaise Pascal.

Question 8

The C.G.S. unit of pressure is :

1. Pa
2. Nm^-2
3. dyne cm^-2
4. dyne cm²

Answer

dyne cm^-2

Reason — C.G.S. unit of pressure is dyne cm^-2 where 1 dyne cm^-2 = 0.1 N m^-2 or 1 N m^-2 = 10 dyne cm^-2

Question 9

One bar is equal to :

1. 10³ Nm^-2
2. 10⁴ Nm^-2
3. 10⁵ Nm^-2
4. 10⁶ Nm²

Answer

10⁵ Nm^-2

Reason — 1 bar = 10⁵ Nm^-2.

Question 10

1 atm of pressure is equal to :

1. 0.076 m of Hg
2. 760 torr
3. 76 torr
4. 7.6 mm of Hg

Answer

760 torr

Reason — torr is a unit of atmospheric pressure after the name of the scientist Torricelli where, 1 torr = 1 mm of Hg and 1 atm = 760 mm of Hg = 760 torr.

Question 11

The pressure on a surface is reduced by :

1. using high thrust
2. increasing the area of surface
3. decreasing the area of surface
4. none of these

Answer

increasing the area of surface

Reason — Larger the area on which a given thrust acts, lesser is the pressure exerted by it, as pressure is inversely proportional to the area of surface.

$\text{Pressure} = \dfrac{\text{Thrust}}{\text{Area}} \\[0.5em] \text{or} \\[0.5em] P = \dfrac{\text{F}}{\text{A}}$

Question 12

Cutting tools have either sharp or pointed edges so that a ............... thrust may cause a ............... pressure at that edges and cutting can be done with less effort.

1. high, high
2. small, small
3. high, small
4. small, high

Answer

small, high

Reason — For a given thrust, the pressure on a surface is increased by reducing the area of surface on which it is acting, hence, cutting tools have either sharp or pointed edges so that a small thrust may cause a high pressure at that edges and cutting can be done with less effort.

Question 13

The pressure inside a liquid of density ρ at a depth h is:

1. hρg
2. h/ρg
3. hρ/g
4. hρ

Answer

hρg

Reason — The three factors on which the pressure at a point in a liquid depends are —

1. depth of the point below the free surface (h)

2. density of liquid (ρ) and

3. acceleration due to gravity (g)

Pressure = hρg

Question 14

Out of the following, which one is correct about the law of liquid pressure ?

1. Pressure is different in all directions about a point inside the liquid.
2. In a stationary liquid, pressure is different at all points on a horizontal plane.
3. Inside the liquid, pressure decreases with an increase in depth from its free surface.
4. It increases with an increase in the density of the liquid.

Answer

It increases with an increase in the density of the liquid.

Reason — As Pressure = hρg, so pressure is directly proportional to the density of the liquid. Hence, it increases with an increase in the density of the liquid.

Question 15

The pressure P₁ at a certain depth in river water and P₂ at the same depth in sea water are related as:

1. P₁ > P₂
2. P₁ = P₂
3. P₁ < P₂
4. P₁ - P₂ = atmospheric pressure

Answer

P₁ < P₂

Reason — As the density of sea water is more than the density of river water, hence, the pressure at a certain depth in sea water is more than that at the same depth in river water because pressure increases with the increase in density of liquid.

Question 16

The pressure P₁ at the top of a dam and P₂ at a depth h from the top inside water (density ρ) are related as:

1. P₁ > P₂
2. P₁ = P₂
3. P₁ - P₂ = hρg
4. P₂ - P₁ = hρg

Answer

P₂ - P₁ = hρg

Reason — The pressure at a point inside a liquid at a depth h is P₂

P₂ = pressure at the top of a dam (P₁) + pressure due to liquid column

= P₁ + hρg

So, P₂ = P₁ + hρg

Hence,

P₂ - P₁ = hρg

Question 17

The wall of a dam is made thicker at the bottom because :

1. the pressure exerted by a liquid remains the same with its depth
2. the pressure exerted by a liquid decreases with its depth
3. the pressure exerted by a liquid increases with its depth
4. of safety from outer forces.

Answer

the pressure exerted by a liquid increases with its depth

Reason — A dam has broader walls at the bottom than at the top as the pressure exerted by the liquid increases with it's depth. Thus, as depth increases, more and more pressure is exerted by water on the walls of the dam.

Question 18

Hydraulic machines work on the principle of :

1. Newton's first law
2. Newton's third law
3. Pascal's law
4. both (a) and (b)

Answer

Pascal's law

Reason — The principle of a hydraulic machine is that a small force applied on a smaller piston is transmitted to produce a large force on the bigger piston. This principle is based on Pascal's law.

Question 19

Hydraulic machines act like a :

1. force subtractor
2. force reducer
3. force multiplier
4. both (a) and (c)

Answer

force multiplier

Reason — The principle of a hydraulic machine is that a small force applied on a smaller piston is transmitted to produce a large force on the bigger piston. Hence, it acts as a force multiplier.

Exercise 4(A) — Very Short Answer Type

Question 1

Define the term thrust. State it's S.I. unit.

Answer

Thrust is the force acting normally on a surface.

The S.I. unit of thrust is newton (N).

Thrust is a vector quantity.

Question 2

(a) What physical quantity is measured in bar ?

(b) How is the unit bar related to the S.I. unit pascal ?

Answer

(a) The physical quantity that is measured in bar is Pressure.

(b) The relation between bar and pascal is 1 bar = 10⁵ pascal.

Question 3

Define one pascal (Pa), the S.I. unit of pressure.

Answer

One pascal is the pressure exerted on a surface of area 1 m² by a force of 1 N acting normally on it.

Question 4

State whether thrust is a scalar or vector?

Answer

Thrust is a vector quantity. Its direction of application is normal to the surface.

Question 5

State whether pressure is a scalar or vector?

Answer

Pressure is a scalar quantity.

Question 6

What is a fluid?

Answer

A substance which can flow is called a fluid. All liquids and gases are thus fluids.

Question 7

Pressure at free surface of a water lake is P₁, while at a point at depth h below it's free surface is P₂. (a) How are P₁ and P₂ related ? (b) Which is more P₁ or P₂ ?

Answer

(a) As we know,

Total pressure in a liquid at a depth h is P₂

= atmospheric pressure acting on the surface (P₁) + pressure due to liquid column (h ρ g)

= P₁ + h ρ g

Hence,

P₂ = P₁ + h ρ g

(b) From the above expression we observe that,

P₂ > P₁

Question 8

How does the liquid pressure on a diver change if —

(i) the diver moves to the greater depth, and

(ii) the diver moves horizontally ?

Answer

(i) When the diver moves to a greater depth the liquid pressure increases as liquid pressure at a point increases with the increase of depth from it's free surface.

(ii) When the diver moves horizontally, the liquid pressure remains unchanged as inside a liquid, pressure is same at all points on a horizontal plane.

Question 9

State Pascal's law of transmission of pressure.

Answer

Pascal's law states that the pressure exerted anywhere in a confined liquid is transmitted equally and undiminished in all directions throughout the liquid.

Question 10

Name two applications of Pascal's law.

Answer

Applications of Pascal's law are —

1. Hydraulic brakes
2. Hydraulic jack

Question 11

Complete the following sentences —

(a) Pressure at a depth h in a liquid of density ρ is ............... .

(b) Pressure is ............... in all directions about a point in a liquid.

(c) Pressure at all points at the same depth is ............... .

(d) Pressure at a point inside a liquid is ............... to it's depth.

(e) Pressure of a liquid at a given depth is ............... to the density of liquid.

Answer

(a) Pressure at a depth h in a liquid of density ρ is h ρ g.

(b) Pressure is same in all directions about a point in a liquid.

(c) Pressure at all points at the same depth is same.

(d) Pressure at a point inside a liquid is directly proportional to its depth.

(e) Pressure of a liquid at a given depth is directly proportional to the density of liquid.

Exercise 4(A) — Short Answer Type

Question 1

What is meant by pressure ? State its S.I. unit.

Answer

Pressure is the thrust per unit area of surface.

$Pressure = \dfrac{Thrust}{Area} \\[0.5em] \text{or} \\[0.5em] P = \dfrac{F}{A}$

Pressure is a scalar quantity.

The S.I. unit of pressure is newton per metre² . This unit is named as pascal (symbol Pa).

Question 2

Differentiate between thrust and pressure.

Answer

Question 3

How does the pressure exerted by a thrust depend on the area of surface on which it acts ? Explain with a suitable example.

Answer

The pressure exerted by a thrust is inversely proportional to the area of surface on which it acts. Larger the area on which a given thrust acts, lesser is the pressure exerted by it.

Example — A brick of weight 4 kgf having dimensions 20 cm x 10 cm x 5 cm, exerts maximum pressure on ground when it is placed with it's longest side (20 cm) vertical, as shown in fig below, while it exerts minimum pressure when it is placed with it's shortest side (5 cm) vertical, even though the thrust is same in each case.

Question 4

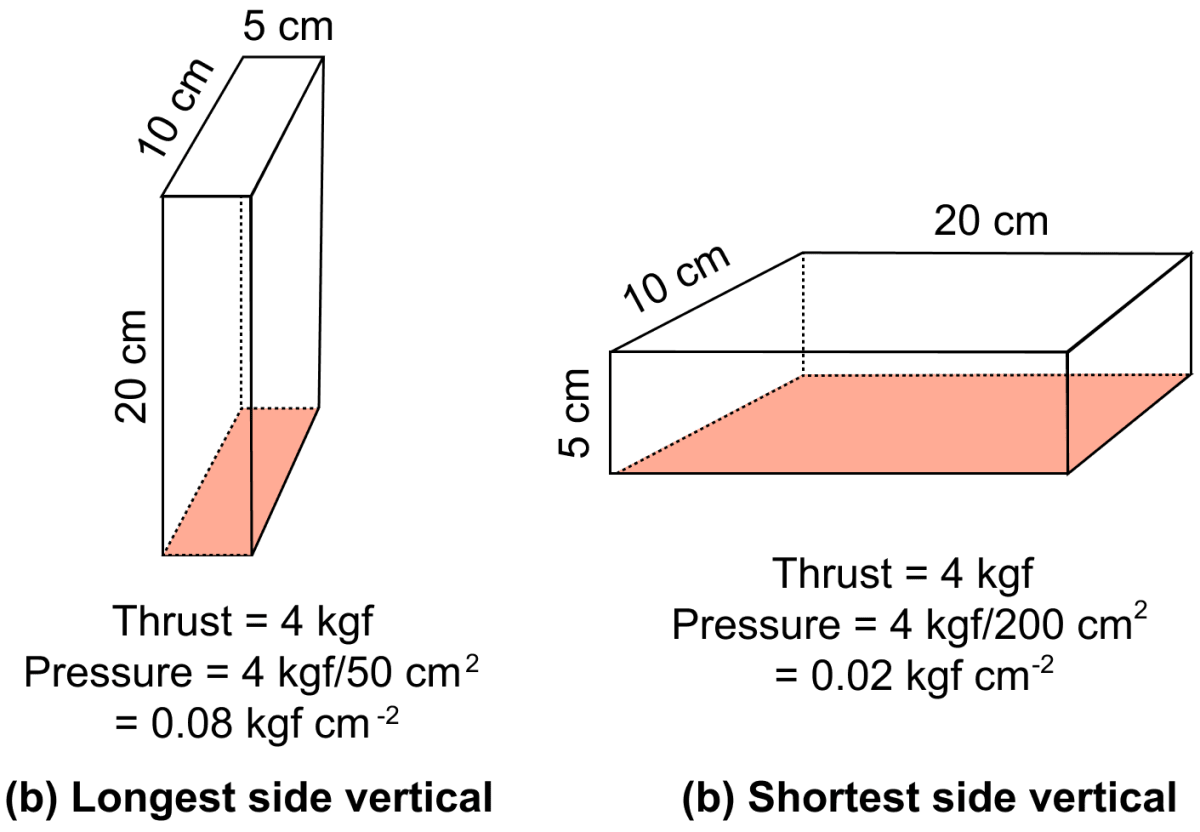
Why is the tip of an allpin made sharp?

Answer

The tip of an allpin is made sharp so that large pressure is exerted through the pointed end and that they can be driven into, with less effort.

Question 5

Explain the following —

(a) It is easier to cut with a sharp knife than with a blunt one.

(b) Sleepers are laid below the rails

Answer

(a) It is easier to cut with a sharp knife than with a blunt knife because in a sharp knife even a small thrust causes a great pressure at the edges and hence, cutting can be done with less effort.

(b) Sleepers are laid below the rails so that the pressure exerted by the iron nails on the ground becomes less.

Question 6

What do you mean by the term fluid pressure?

Answer

A fluid contained in a vessel exerts pressure at all points and in all directions due to it's weight and this pressure is called fluid pressure.

Question 7

How does the pressure exerted by a solid and a fluid differ ?

Answer

Both liquids and solids exert pressure due to it's weight, however, pressure exerted by a solid acts only on the surface on which it is placed i.e. at it's bottom, but pressure exerted by a fluid acts on the bottom as well as the walls of the container due to it's tendency to flow.

Question 8

State three factors on which the pressure at a point in a liquid depends.

Answer
The three factors on which the pressure at a point in a liquid depends are —

1. depth of the point below the free surface (h),

2. density of liquid (ρ), and

3. acceleration due to gravity (g).

Question 9

Write an expression for the pressure at a point inside a liquid. Explain the meaning of the symbols used.

Answer

The pressure at a point inside a liquid at a depth h

= Atmospheric pressure + pressure due to liquid column

= P₀ + hρg

where,

P₀ = atmospheric pressure acting on the free surface of liquid

h = depth of the point below the free surface

ρ = the density of the fluid

g = acceleration due to gravity.

Question 10

How does the pressure at a certain depth in sea water differ from that at the same depth in river water ? Explain your answer.

Answer

The pressure at a certain depth in sea water is more than the same depth in river water because the density of sea water is more than the density of river water.

According to the formula,

Pressure = depth x density of liquid x acceleration due to gravity = h ρ g

Therefore, when density of a liquid is more then the pressure exerted is also more as density and pressure are directly proportional.

Question 11

Explain why a gas bubble released at the bottom of a lake grows in size as it rises to the surface of lake.

Answer

It is noticed that as the gas bubble formed at the bottom of the lake rises, it grows in size. The reason is that when the bubble is at the bottom of the lake, total pressure exerted on it is the sum of the atmospheric pressure and the pressure due to the water column above it.

As the gas bubble rises, due to decrease in depth, the pressure due to water column decreases, so the total pressure on the bubble decreases.

According to Boyle's law, the volume of a gas is inversely proportional to the pressure on it. Therefore, the volume of bubble increases due to the decrease in pressure, i.e., the bubble grows in size.

When the bubble reaches the surface of liquid, total pressure exerted on it becomes minimum, just equal to the atmospheric pressure and so the size of bubble when touching the surface becomes maximum.

Question 12

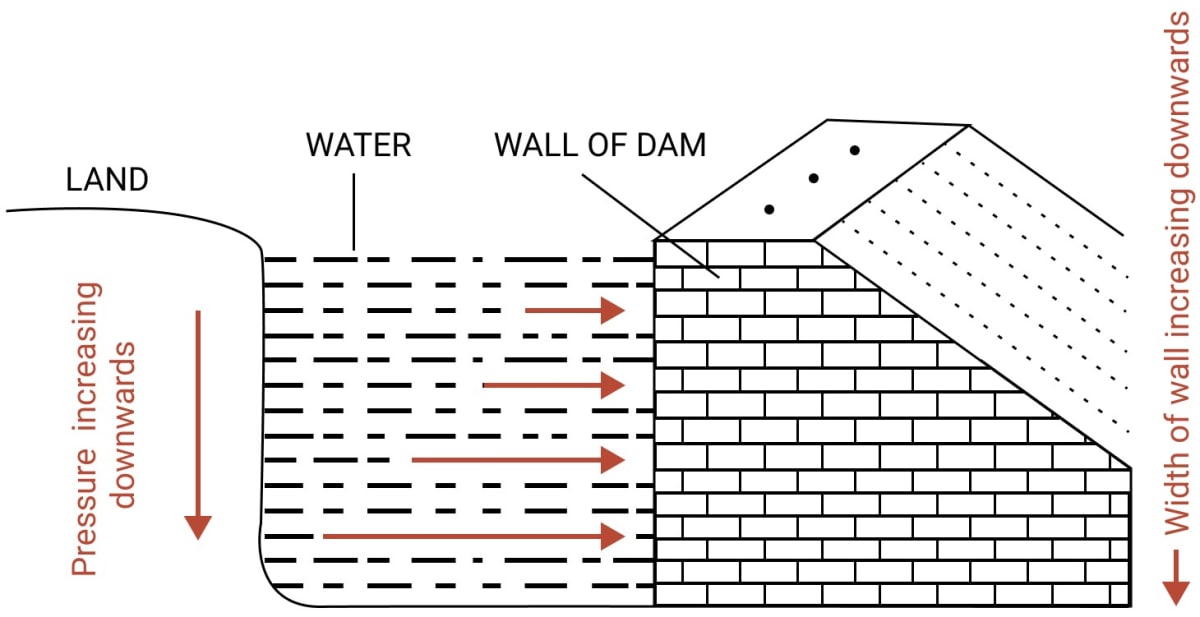
A dam has broader walls at the bottom than at the top. Explain.

Answer

A dam has broader walls at the bottom than at the top as the pressure exerted by the liquid increases with it's depth. Thus, as depth increases, more and more pressure is exerted by water on the walls of the dam.

A thicker wall is required to withstand a greater pressure, therefore, the wall of a dam is made with thickness increasing towards the base.

In the figure given below, the increasing length of arrows in water represents the increasing pressure on the wall of the dam towards the bottom.

Question 13

Why do sea divers need special protective suit ?

Answer

Sea divers need special protective suit to wear because in deep sea, the total pressure exerted on the diver's body is much more than his blood pressure. To withstand it, they need to wear a special protective suit, made from glass reinforced plastic or cast aluminium. The pressure inside the suit is maintained at one atmosphere.

Question 14

State the laws of liquid pressure.

Answer

The laws of liquid pressure are —

1. Inside the liquid, pressure increases with the increase in depth from it's free surface.

2. In a stationary liquid, pressure is same at all points on a horizontal plane.

3. Pressure is same in all directions about a point inside the liquid.

4. Pressure at same depth is different in different liquids. It increases with the increase in density of liquid.

5. A liquid seeks it's own level.

Question 15

A tall vertical cylinder filled with water is kept on a horizontal table top. Two small holes A and B are made on the wall of the cylinder, A near the middle and B just below the free surface of water. State and explain your observation.

Answer

We observe that the throw of the liquid from hole A is more than the B i.e., the liquid reaches to a greater distance on the horizontal surface from hole A than hole B. This shows that liquid pressure at a point increases with the increase of depth from it's free surface.

Question 16

Name and state the principle on which a hydraulic press works. Write one use of the hydraulic press.

Answer

A hydraulic press works on the principle of Pascal's law.

Principle — When a force F₁ is applied on the piston A, it exerts a pressure on liquid contained in the cylinder P. According to Pascal's law, this pressure is transmitted through liquid in tube R to the piston B of the other cylinder Q due to which the piston B tends to move upwards.

Since, the area of cross section of cylinder P is less than that of the cylinder Q, therefore by applying a small force on the piston A, we can lift a large weight kept on the piston B.

When no weight is placed on the piston B, it rises up against a fixed roof with a force F₂ (F₂ > F₁). If a bale of cotton is kept on the press plunger B, it gets compressed.

Use of hydraulic press — It is used for pressing cotton bales and goods such as books, quilts etc.

Exercise 4(A) — Long Answer Type

Question 1

Describe a simple experiment to demonstrate that a liquid enclosed in a vessel exerts pressure in all directions.

Answer

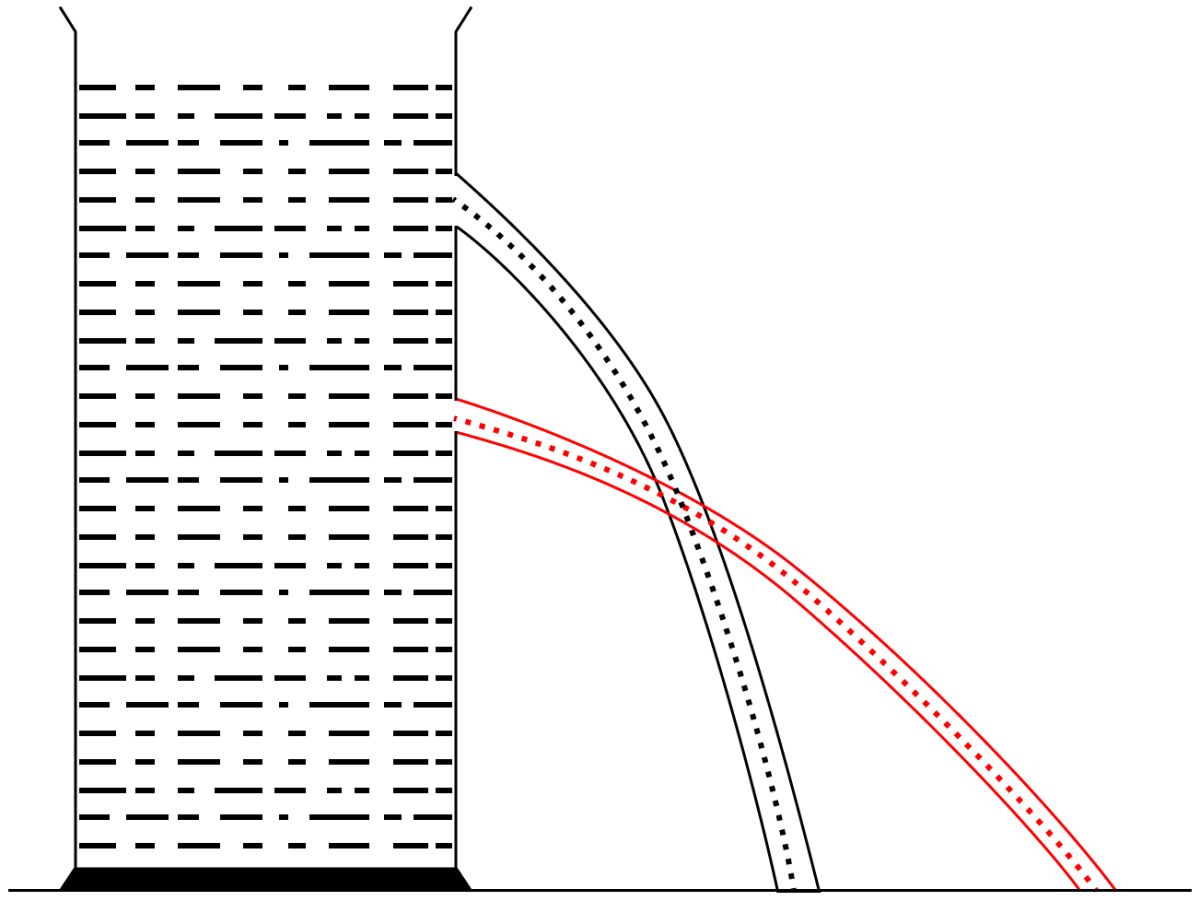
Take a vessel filled with a liquid (say, water). Place it on a horizontal surface. Make several small holes in the wall of the vessel anywhere below the free surface of liquid. It is observed that liquid spurts out through each hole. This shows that the liquid exerts pressure at each point on the wall of the vessel.

Question 2

Deduce an expression for the pressure at a depth inside a liquid.

Answer

Consider a vessel containing a liquid with density ρ. Let the liquid be stationary. In order to calculate pressure at a depth h, consider a horizontal circular surface PQ with area A at depth h below the free surface XY of the liquid as shown below.

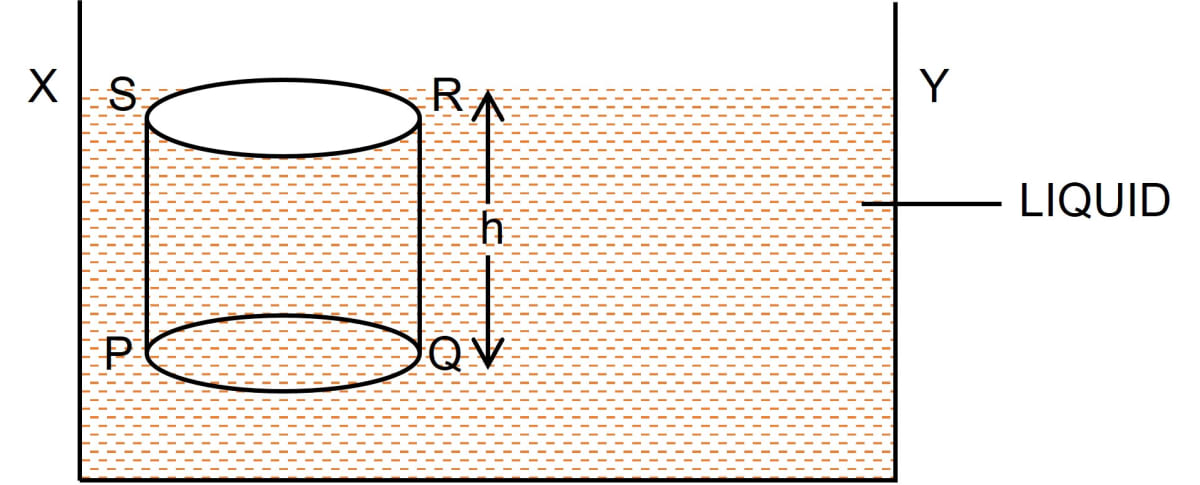
The pressure on surface PQ will be due to the weight of the liquid column above the surface PQ, (i.e., the liquid contained in cylinder PQRS of height h with PQ as it's base and top face RS lying on the free surface XY of the liquid).

Thrust exerted on the surface PQ

= Weight of the liquid column PQRS

= Volume of liquid column PQRS x density x g

= (Area of base PQ x height) x density x g

= (A x h) ρ x g = A h ρ g

This thrust is exerted on the surface PQ of area A. Therefore, pressure

P = $\dfrac{\text{Thrust on surface}}{\text{Area of surface}}$ = $\dfrac{\text{A h ρ g}}{\text{A}}$ = h ρ g

Hence, Pressure = depth x density of liquid x acceleration due to gravity = h ρ g

Question 3

Explain the principle of a hydraulic machine. Name two devices which work on this principle.

Answer

The principle of hydraulic machine is that a small force applied on a smaller piston is transmitted to produce a large force on the bigger piston.

Two devices that work on this principle are —

1. Hydraulic brakes
2. Hydraulic jack

Question 4

The diagram in figure shows a device which makes use of the principle of transmission of pressure.

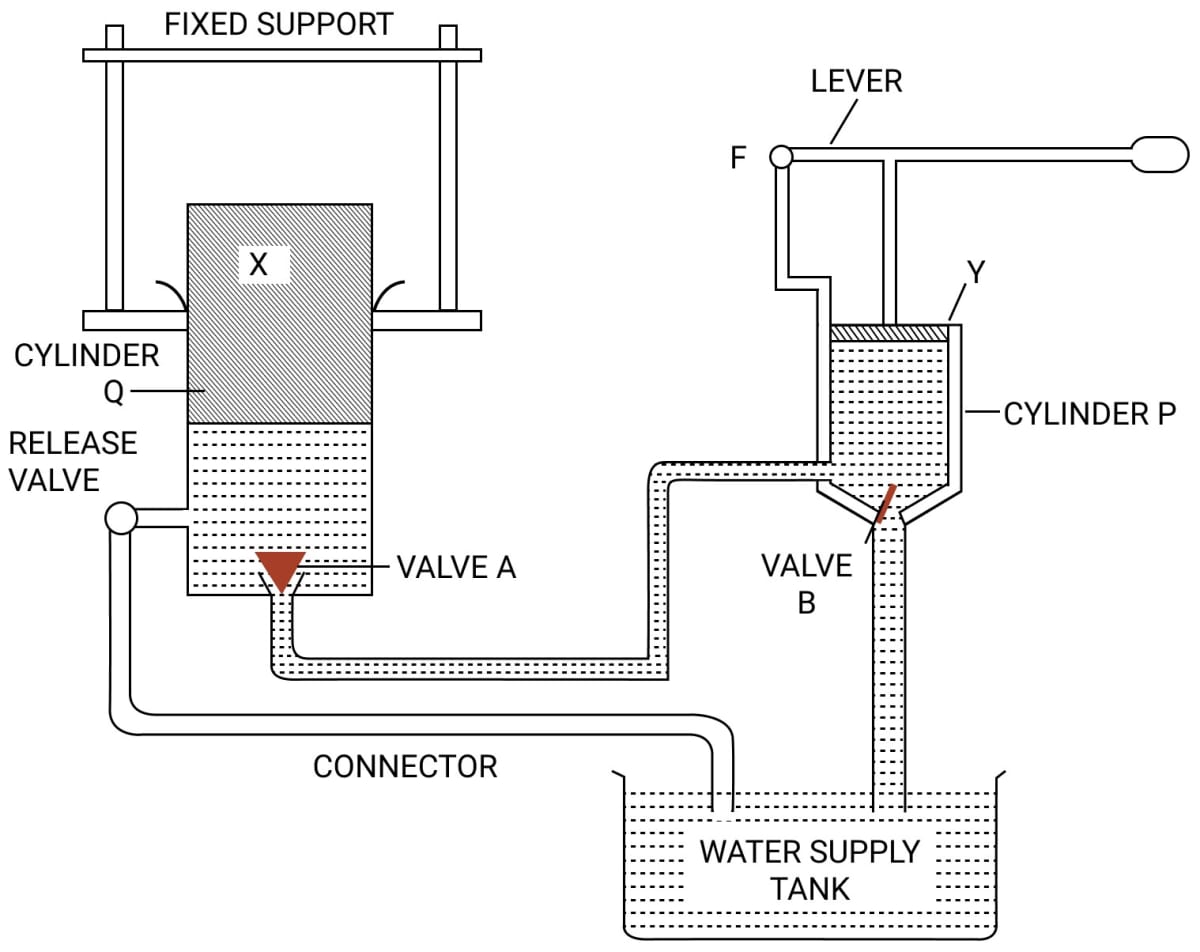
(i) Name the parts labelled by the letters X and Y.

(ii) Describe what happens to the valves A and B and to the quantity of water in the two cylinders when the lever arm is moved down.

(iii) Give reasons for what happens to the valves A and B in part (ii).

(iv) What happens when the release valve is opened ?

(v) What happens to the valve B in cylinder P when the lever arm is moved up ?

(vi) Give a reason for your answer in part (v)

(vii) State one use of the above device.

Answer

(i) The parts are —

X → Press plunger

Y → Pump plunger

(ii) When the lever arm is moved down, the valve B closes and the valve A opens, so water from cylinder P is forced into the cylinder Q.

(iii) When the lever arm is moved down, the valve B closes due to an increase in pressure in cylinder P. Now pressure from cylinder P is transmitted to the connecting pipe. As the pressure in connecting pipe becomes greater than the cylinder Q, the valve A opens, so water from cylinder P is forced into the cylinder Q.

(iv) When the release valve is opened the ram (or press) plunger Q gets lowered and water of the cylinder Q runs out into the reservoir.

(v) When the lever arm is moved up the valve B opens upwards.

(vi) When the lever arm is moved up the valve B opens upward because the pressure in cylinder P decreases.

(vii) An hydraulic press is used for pressing cotton bales and goods like quilts, books, etc.

Question 5

Draw a simple diagram of a hydraulic jack and explain it's working.

Answer

When handle H of lever is pressed down by applying an effort, the valve V opens because of increase in pressure in the cylinder P. The liquid runs out from the cylinder P to the cylinder Q.

As a result, the piston B rises up and it raises the car placed on the platform. When the car reaches the desired height, the handle H of lever is no longer pressed.

The valve V gets closed (since the pressure on either side of the valve becomes same) so that the liquid may not run back from the cylinder Q to the cylinder P.

Question 6

Explain the working of a hydraulic brake with a simple labelled diagram.

Answer

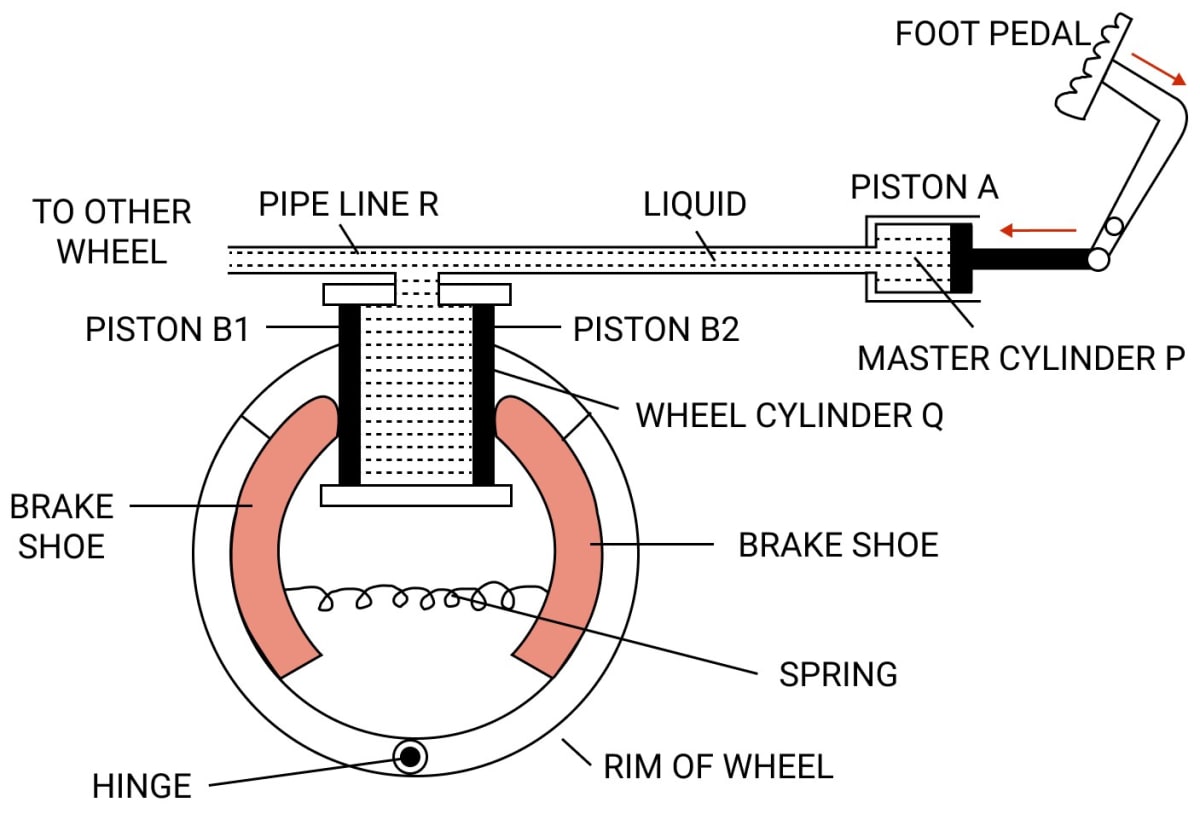
To apply brakes, the foot pedal is pressed due to which pressure is exerted on the liquid in the master cylinder P, so liquid runs out from the master cylinder P to the wheel cylinder Q.

As a result, the pressure is equally transmitted and undiminished through the liquid to the pistons B₁ and B₂ of the wheel cylinder Q. Therefore, the pistons B₁ and B₂ gets pushed outwards and brake shoes gets pressed against the rim of the wheel due to which the motion of the wheel retards.

Since, the area of cross section of piston A in the master cylinder P is less than that in the wheel cylinder Q, a small force applied at the foot pedal produces a large force on the pistons B₁ and B₂ of the wheel cylinder Q.

This is the force responsible for retarding the vehicle. It should be noted that due to transmission of pressure through liquid, equal pressure is exerted on all wheels of the vehicle connected to the pipe line R.

On releasing the pressure on the pedal, the spring pulls the brake shoes to it's original position and forces the piston's B₁ and B₂ to return back into the wheel cylinder Q. As a result the liquid runs back from the wheel cylinder Q to the master cylinder P and thus the brakes gets released.

Exercise 4(A) — Numericals

Question 1

A hammer exerts a force of 1.5 N on each of the two nails A and B. The area of cross section of tip of nail A is 2 mm² while that of nail B is 6 mm² . Calculate pressure on each nail in pascal.

Answer

As we know,

Pressure (P) = $\dfrac{\text {Thrust (F)}}{\text {Area (A)}}$

Given,

F = 1.5 N

A = 2 mm²

Converting 2 mm² in metre²

As 1 mm = $\dfrac{1}{1000}$ m

So, 1 mm² = (1) mm x (1) mm

= $(\dfrac{1}{1000}) m \times (\dfrac{1}{1000}) m$

= 1 x 10 ^-6 m²

Hence,

2 mm² = 2 x 10^-6 m²

A_A = 2 x 10 ^-6 m²

A_B = 6 x 10 ^-6 m²

Substituting the values in the formula above, we get,

Pressure on A

$P = \dfrac{1.5}{2 \times 10^{-6}} \\[0.5em] P = 0.75 \times 10^{6} \\[0.5em] \Rightarrow P = 7.5 \times 10^{5} Pa \\[0.5em]$

Hence, Pressure on A = 7.5 x 10⁵ Pa

Pressure on B

$P = \dfrac{1.5}{6 \times 10^{-6}} \\[0.5em] P = 0.25 \times 10^{6} \\[0.5em] \Rightarrow P = 2.5 \times 10^{5} Pa \\[0.5em]$

Hence, Pressure on B = 2.5 x 10⁵ Pa

Question 2

A block of iron of mass 7.5 kg and of dimensions 12 cm x 8 cm x 10 cm is kept on a table top on it's base of side 12 cm x 8 cm. Calculate (a) thrust and (b) pressure exerted on the table top. Take 1 kgf = 10 N.

Answer

As we know,

(a) Force (F) = mass (m) x acceleration due to gravity (g)

Given,

m = 7.5 kg

1 kgf = 10 N

Substituting the values in the formula above we get,

$F = 7.5 \times 10 \\[0.5em] \Rightarrow F = 75 N$

Hence, F = 75 N

(b) As we know,

Pressure (P) = $\dfrac{\text {Thrust (F)}}{\text {Area (A)}}$

Given,

Area of the base = 12 x 8 = 96 cm²

Converting cm² into m²

100 cm = 1 m

So, 100 cm x 100 cm = 1 m²

Hence, 96 cm² = $\dfrac{1 \times 96}{10000}$

Therefore, A = 0.0096 m ²

Substituting the values in the formula above, we get,

$P = \dfrac{75}{0.0096} \\[0.5em] \Rightarrow P = 7812.5.5 Pa \\[0.5em]$

Hence,

Pressure = 7812.5 Pa

Question 3

A vessel contains water up to a height of 1.5 m. Taking the density of water 10 ³ kg m ^-3, acceleration due to gravity 9.8 m s ^-2 and area of base vessel 100 cm ², calculate (a) the pressure and (b) the thrust, at the base of vessel.

Answer

(a) As we know,

Pressure due to water column of height h = h ρ g

Given,

h = 1.5 m

ρ = 1000 kg m ^-3

g = 9.8 m s ²

Substituting the values in the formula above, we get,

$P = 1.5 \times 1000 \times 9.8 \\[0.5em] P = 14.7 \times 10^{3} \text {N m}^{-2} \\[0.5em]$

Hence, pressure = 1.47 x 10⁴ N m^-2

(b) As we know,

Pressure (P) = $\dfrac{\text {Thrust (F)}}{\text {Area (A)}}$

Given,

A = 100 cm ²

Converting cm ² into m ²

100 cm = 1 m

So, 100 cm x 100 cm = 1 m ²

Hence, 100 cm ² = $\dfrac{1 \times 100}{10000}$

Therefore, A = 10^-2 m ²

Substituting the values in the formula above, we get,

$1.47 \times 10^{4} = \dfrac{\text {Thrust (F)}}{10^{-2}} \\[0.5em] \Rightarrow \text {Thrust (F)} = 1.47 \times 10^{2} \\[0.5em] \Rightarrow \text {Thrust (F)} = 147 N \\[0.5em]$

Hence, Thrust = 147 N

Question 4

The area of base of a cylindrical vessel is 300 cm ². Water (density = 1000 kg m ^-3) is poured into it up to a depth of 6 cm. Calculate (a) the pressure and (b) the thrust of water on the base. (g = 10 m s^-2).

Answer

(a) As we know,

Pressure due to water column of height h = hρg

Given,

ρ = 1000 kg m ^-3

g = 10 m s^-2

h = 6 cm

Converting cm to m

100 cm = 1 m

So, 6 cm = $\dfrac{1}{100}$ x 6 = 0.06 m

Hence, h = 0.06 m

Substituting the values in the formula above we get,

$P = 0.06 \times 1000 \times 10 \\[0.5em] P = 600 \text {Pa} \\[0.5em]$

Hence, Pressure = 600 Pa

(b) As we know,

Pressure (P) = $\dfrac{\text {Thrust (F)}}{\text {Area (A)}}$

A = 300 cm ²

Converting cm ² into m ²

100 cm = 1 m

So, 100 cm x 100 cm = 1 m ²

Hence, 300 cm ² = $\dfrac{1 \times 300}{10000}$

Therefore, A = 3 x 10^-2 m ²

Substituting the values in the formula we get,

$600 = \dfrac{\text {Thrust (F)}}{3 \times 10^{-2}} \\[0.5em] \Rightarrow \text {Thrust (F)} = 600 \times 3 \times 10^{-2}\\[0.5em] \Rightarrow \text {Thrust (F)} = 18 N \\[0.5em]$

Hence, thrust = 18 N

Question 5

(a) Calculate the height of a water column which will exert on it's base the same pressure as the 70 cm column of mercury. Density of mercury is 13.6 g cm^-3.

(b) Will the height of the water column in part (a) change if the cross section of the water column is made wider ?

Answer

(a) As we know,

Pressure due to water column of height h = hρg

and

Pascal's law, states that the pressure exerted anywhere in a confined liquid is transmitted equally and undiminished in all directions throughout the liquid.

Hence,

Pressure due to water column = Pressure due to mercury column

Hence,

h_w ρ_w g = h_m ρ_m g

Given,

h_m = 70 cm

ρ_m = 13.6 g cm^-3

ρ_w = 1 g cm^-3

From the above formula, we get,

h_w = $\dfrac{h_m ρ_m}{ρ_w}$

Substituting the values, we get,

$h_w = (\dfrac{13.6}{1}) \times 70 \\[0.5em] \Rightarrow h_w = 952 \text{cm} \\[0.5em] \Rightarrow h_w = 9.52 \text{m} \\[0.5em]$

Hence, height of a water column = 9.52 m

(b) No, if the cross section of the water column is made wider, the height of the water column will be unaffected.

Question 6

The pressure of water on the ground floor is 40,000 Pa and on the first floor is 10,000 Pa. Find the height of the first floor.
(Take : density of water = 1000 kg m^-3, g = 10 m s^-2)

Answer

(i) As we know,

Pressure due to water column of height h = h ρ g

Given,

density of water = 1000 kg m ^-3

g = 10 m s^-2

P_w on ground floor = 40,000 Pa

P_w on first floor Pwf = 10,000 Pa

In order to know the height of the first floor, let us calculate the difference in pressure

P = P_wg - P_wf = 40,000 – 10,000 = 30,000 Pa

Substituting the values in the formula,

$P = h ρ g \\[0.5em] 30,000 = 1000 \times 10 \times h \\[0.5em] h = 3 m \\[0.5em]$

Hence, the height of the first floor = 3 m.

Question 7

A simple U tube contains mercury to the same level in both of it's arms. If water is poured to a height of 13.6 cm in one arm, how much will be the rise in mercury level in the other arm ?

Given: density of mercury = 13.6 x 10³ kg m^-3 and density of water = 10³ kg m^-3

Answer

Given,

ρ_m = 13.6 x 10³ kg m ^-3

ρ_w = 10³ kg m ^-3

Height to which water is poured in one arm, h_w = 13.6 cm

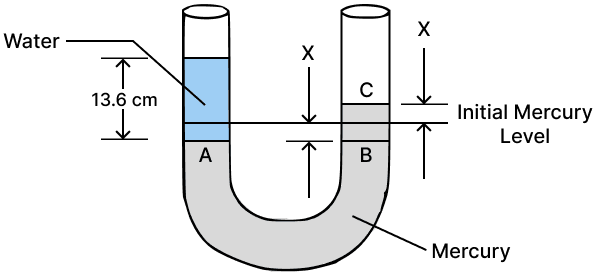
By pouring 13.6 cm of water, the mercury level in the left arm goes down to point A by x cm, while in the right arm, it rises to point C by x cm. Therefore, BC = h_m = 2x cm

By Pascal's law,

Pressure in the water column = pressure in the mercury column

Therefore, P_A = P_B

⇒ h_w ρ_w g = h_m ρ_m g

⇒ 13.6 x 10³ x g = 2𝑥 x 13.6 x 10³ x g

⇒ 1 = 2𝑥

⇒ 𝑥 = $\dfrac{1}{2}$ = 0.5 cm

Hence, the rise in mercury level = 0.5 cm

Question 8

In a hydraulic machine, a force of 2 N is applied on the piston of area of cross section 10 cm ². What force is obtained on it's piston of area of cross section 100 cm ²?

Answer

As we know,

Pressure (P) = $\dfrac{\text {Thrust (F)}}{\text {Area (A)}}$

Given,

A = 10 cm ²

Converting cm ² into m ²

100 cm = 1 m

So, 100 cm x 100 cm = 1 m ²

Hence, 10 cm ² = $\dfrac{1 \times 10}{10000}$

Therefore, A = 10^-3 m ²

F = 2 N at area of cross section 10 cm ²

Substituting the values in the formula we get,

P = $\dfrac{2}{10^{-3}}$     [Equation 1]

Now when, A = 100 cm ²

Converting cm ² into m ²

100 cm = 1 m

So, 100 cm x 100 cm = 1 m ²

Hence, 100 cm ² = $\dfrac{1 \times 100}{10000}$

Therefore, A = 10^-2 m ²

Substituting the value in the formula above we get,

Therefore, P = $\dfrac{F}{10^{-2}}$     [Equation 2]

Equating 1 and 2 we get,

$\dfrac{2}{10^{-3}} = \dfrac{F}{10^{-2}} \\[0.5em] \Rightarrow F = \dfrac{2 \times 10^{-2} }{10^{-3}} \\[0.5em] \Rightarrow F = 20 N$

Hence, force at 100 cm ² = 20 N

Question 9

What should be the ratio of area of cross section of the master cylinder and wheel cylinder of a hydraulic brake so that a force of 15 N can be obtained at each of it's brake shoe by exerting a force of 0.5 N on the pedal ?

Answer

As we know,

Pressure (P) = $\dfrac{\text {Thrust (F)}}{\text {Area (A)}}$

Let,

area of cross section of the master cylinder = A₁

area of cross section of the wheel cylinder = A₂

force applied on pedal be F₁ = 0.5 N

force applied on brake shoe F₂ = 15 N

By the principle of hydraulic brakes which works on Pascal's law

Pressure on narrow piston = pressure on broader piston

Hence,

$\dfrac{F_{1}}{A_{1}} = \dfrac{F_{2}}{A_{2}} \\[0.5em] \dfrac{0.5}{A_{1}} = \dfrac{15}{A_{2}} \\[0.5em] \dfrac{A_{1}}{A_{2}} = \dfrac{0.5}{15} \\[0.5em] \Rightarrow \dfrac{A_{1}}{A_{2}} = \dfrac{5}{150} \\[0.5em] \Rightarrow \dfrac{A_{1}}{A_{2}} = \dfrac{1}{30} \\[0.5em]$

Hence, the ratio of area of cross section = 1 : 30

Question 10

The areas of pistons in a hydraulic machine are 5 cm ² and 625 cm ². What force on the smaller piston will support a load of 1250 N on the larger piston ? State any assumption which you make in your calculation.

Answer

As we know,

Pressure (P) = $\dfrac{\text {Thrust (F)}}{\text {Area (A)}}$

and by the principle of hydraulic machine

Pressure on narrow piston = pressure on broader piston

Hence,
$\dfrac{F_{1}}{A_{1}} = \dfrac{F_{2}}{A_{2}} \\[0.5em]$

Given,

Area of narrow piston (A₁) = 5 cm ²

Area of wider piston (A₂) = 625 cm ²

force (F₂) = 1250 N

Substituting the values in the formula above we get,

$\dfrac{F_{1}}{5} = \dfrac{1250}{625} \\[0.5em] F_{1} = \dfrac{1250 \times 5 }{625} \\[0.5em] \Rightarrow F_{1} = 10 N \\[0.5em]$

Hence, force acting on the smaller piston = 10 N

Assumption — There is no friction and no leakage of liquid.

Question 11

(a) The diameter of neck and bottom of a bottle are 2 cm and 10 cm respectively. The bottle is completely filled with oil. If the cork in the neck is pressed in with a force of 1.2 kgf, what force is exerted on the bottom of the bottle ?

(b) Name the law/principle you have used to find the force in part (a)

Answer

(a) As we know,

Pressure (P) = $\dfrac{\text {Thrust (F)}}{\text {Area (A)}}$

and by the principle of hydraulic machine

Pressure on neck = pressure on bottom of bottle

Hence,

$\dfrac{F_{1}}{A_{1}} = \dfrac{F_{2}}{A_{2}} \\[0.5em]$

Given,

Diameter of neck (d₁) = 2 cm

Hence, A₁ = 𝜋 $(\dfrac{2}{2})^{2}$ = 𝜋

Diameter of bottom of bottle (d₂) = 10 cm

Hence, A₂ = 𝜋 $(\dfrac{10}{2})^{2}$ = 25 𝜋

Force applied on the cork in the neck (F₁) = 1.2 kgf

Substituting the values in the formula above we get,

$\dfrac{1.2}{\pi} = \dfrac{F_{2}}{25\pi} \\[0.5em] F_{2} = 1.2 \times 25 \\[0.5em] F_{2} = 30 \text{ kgf} \\[0.5em]$

Hence, force exerted at the bottom of the neck = 30 kgf.

(b) The Pascal's law is applied to solve the part (a) which states that the pressure exerted anywhere in a confined liquid is transmitted equally and undiminished in all directions throughout the liquid.

Hence,

$\dfrac{F_{1}}{A_{1}} = \dfrac{F_{2}}{A_{2}} \\[0.5em]$

Question 12

A force of 50 kgf is applied to the smaller piston of a hydraulic machine. Neglecting friction, find the force exerted on the large piston, if the diameters of the pistons are 5 cm and 25 cm respectively.

Answer

(a) As we know, by the principle of hydraulic machine

Pressure on the smaller piston = pressure on the larger piston

Hence,

$\dfrac{F_{1}}{A_{1}} = \dfrac{F_{2}}{A_{2}} \\[0.5em]$

Given,

Diameter of the smaller piston (d₁) = 5 cm

Hence, A₁ = 𝜋 $(\dfrac{5}{2})^{2}$ = 6.25 𝜋

Diameter of the larger piston (d₂) = 25 cm

Hence, A₂ = 𝜋 $(\dfrac{25}{2})^{2}$ = 156.25 𝜋

Force applied on the smaller piston (F₁) = 50 kgf

Substituting the values in the formula above we get,

$\dfrac{50}{6.25 \pi} = \dfrac{F_{2}}{156.25\pi} \\[0.5em] F_{2} = \dfrac{50 \times 156.25}{6.25} = \\[0.5em] F_{2} = 1250 kgf \\[0.5em]$

Hence, force exerted on the larger piston = 1250 kgf.

Question 13

Two cylindrical vessels fitted with pistons A and B of area of cross section 8 cm ² and 320 cm ² respectively, are joined at their bottom by a tube and they are completely filled with water. When a mass of 4 kg is placed on piston A, find : (i) the pressure on piston A, (ii) the pressure on piston B, and (iii) the thrust on piston B.

Answer

(i) As we know,

Pressure (P) = $\dfrac{\text {Thrust (F)}}{\text {Area (A)}}$

Given,

Force on the narrow piston A = 4 kg

A_A = 8 cm ²

A_B = 320 cm ²

Substituting the values in the formula above, we get,

$P_A = \dfrac{4}{8} \\[0.5em] \Rightarrow P = 0.5 \text { kg cm}^{-2} \\[0.5em]$

Hence, P_A = 0.5 kg cm^-2

(ii) As we know, by the principle of hydraulic machine

Pressure on piston A = pressure on piston B

Hence, P_B = 0.5 kg cm^-2

(iii) Thrust on piston B is acting in the upward direction, which is given by

Pressure (P) = $\dfrac{\text {Thrust (F)}}{\text {Area (A)}}$

Substituting the values, we get,

$0.5 = \dfrac{\text{thrust}}{320} \\[0.5em] \Rightarrow \text{thrust} = 0.5 \times 320 \\[0.5em] \Rightarrow \text{thrust} = 160 \text{kgf} \\[0.5em]$

Hence, thrust on piston B = 160 kgf

Question 14

What force is applied on a piston of area of cross section 2 cm ² to obtain a force 150 N on the piston of area of cross section 12 cm ² in a hydraulic machine ?

Answer

As we know, by the principle of hydraulic machine

Pressure on piston A = pressure on piston B

Hence,

$\dfrac{F_{1}}{A_{1}} = \dfrac{F_{2}}{A_{2}} \\[0.5em]$

Given,

A₁ = 2 cm ²

Converting cm ² into m ²

100 cm = 1 m

So, 100 cm x 100 cm = 1 m ²

Hence, 2 cm ² = $\dfrac{1 \times 2}{10000}$

Therefore, A₁ = 2 x 10^-4 m ²

A₂ = 12 cm ²

Hence, 12 cm ² = $\dfrac{1 \times 12}{10000}$

Therefore, A₂ = 12 x 10^-4 m ²

F₂ = 150 N

Substituting the values in the formula above we get,

$\dfrac{F_1}{2 \times 10^{-4}} = \dfrac{150}{12 \times 10^{-4}} \\[0.5em] \Rightarrow F_1 = \dfrac{150 \times 2 \times 10^{-4}}{12 \times 10^{-4}} \\[0.5em] \Rightarrow F_1 = 25 N \\[0.5em]$

Hence, force applied = 25 N

Exercise 4(B) — Multiple Choice Type

Question 1

The thrust exerted per unit area on the earth's surface due to a column of air is called :

1. pressure
2. atmospheric pressure
3. density
4. buoyancy

Answer

atmospheric pressure

Reason — The thrust exerted per unit area on the earth's surface due to column of air, is called atmospheric pressure on the surface of earth.

Question 2

The normal atmospheric pressure is :

1. 76 m of Hg
2. 76 cm of Hg
3. 76 Pa
4. 76 N m^-2

Answer

76 cm of Hg

Reason — As we know that, barometric height at normal temperature and pressure at sea level is 76 cm of Hg and barometric height is the measure of the atmospheric pressure. Hence, normal atmospheric pressure = 76 cm of Hg.

Question 3

The unit torr is related to the barometric height as:

1. 1 torr = 1 cm of Hg
2. 1 torr = 0.76 cm of Hg
3. 1 torr = 1 mm of Hg
4. 1 torr = 1 m of Hg

Answer

1 torr = 1 mm of Hg

Reason — torr is a unit of atmospheric pressure after the name of the scientist Torricelli where, 1 torr = 1 mm of Hg.

Question 4

The atmospheric pressure at earth surface is P₁ and inside mine is P₂. They are related as:

1. P₁ = P₂
2. P₁ > P₂
3. P₁ < P₂
4. P₂ = 0

Answer

P₁ < P₂

Reason — Atmospheric pressure increases with depth. Hence, P₁ < P₂.

Question 5

Nose bleeding occurs at high altitudes because :

1. the blood pressure becomes less than the atmospheric pressure
2. the blood pressure becomes equal to the atmospheric pressure
3. the blood pressure becomes more than the atmospheric pressure
4. not related with atmospheric pressure.

Answer

the blood pressure becomes more than the atmospheric pressure

Reason — At high altitude, the atmospheric pressure becomes less. Thus, the blood pressure becomes more than the atmospheric pressure and nose bleeding may occur.

Question 6

Simple barometer was first designed by :

1. Sir Issac Newton
2. Pascal
3. Torricelli
4. Thomas Alva Edison

Answer

Torricelli

Reason — In 1643, Torricelli first designed a simple barometer using mercury as the barometric liquid.

Question 7

A barometer is used :

1. to measure atmospheric pressure
2. for weather forecasting
3. as an altimeter to measure heights
4. all of the above

Answer

all of the above

Reason — Measuring atmospheric pressure, weather forecasting, measuring heights, all these are valid uses of a barometer.

Question 8

At the summit of Mount Everest, the atmospheric pressure is :

1. only 40% of the atmospheric pressure at sea level
2. only 60% of the atmospheric pressure at sea level
3. only 30% of the atmospheric pressure at sea level
4. only 50% of the atmospheric pressure at sea level

Answer

only 30% of the atmospheric pressure at sea level

Reason — At the summit of Mount Everest, the atmospheric pressure is only 30% of the atmospheric pressure at sea level.

Question 9

At high altitudes, the atmospheric pressure is :

1. less
2. high
3. high due to strong winds
4. low due to the cloud floating above.

Answer

less

Reason — Atmospheric pressure decreases with altitude due to (1) decrease in height of air column, (2) decrease in density of air.

Question 10

Mercury is preferred as a barometric liquid because :

1. its density is high
2. its vapour pressure is negligible
3. it neither wets nor sticks to the glass
4. all of the above

Answer

all of the above

Reason — Uses of mercury as a barometric liquid are —

1. The density of mercury is greater than that of any liquid, so only 0.76 m of height of mercury is needed to balance the normal atmospheric pressure. Use of other liquids will require a much longer tube.
2. The vapour pressure of mercury is negligible, so the vapours in the torricellian vacuum does not affect the barometric height.
3. Mercury neither wets nor sticks to the glass tube, therefore it gives accurate reading.

Question 11

Which of the following properties of water is incorrect regarding its non-usage as a barometric liquid?

1. It neither wets nor sticks to the glass tube
2. The vapour pressure of water is high
3. The surface of water cannot be easily seen while taking observations
4. The density of water is low.

Answer

It neither wets nor sticks to the glass tube

Reason — Water sticks to the glass tube and wets it, so the reading becomes inaccurate.

Question 12

If the barometric height gradually falls, it indicates :

1. a possibility of a storm or cyclone
2. extremely dry weather
3. weather will remain the same.
4. a possibility of rain.

Answer

a possibility of rain.

Reason — If the barometric height gradually falls, it indicates that the moisture is increasing i.e., there is a possibility of rain.

Question 13

The atmospheric pressure ............... with rising altitudes as the density of air ............... .

1. increases, decreases
2. decreases, increases
3. decreases, decreases
4. increases, increases

Answer

decreases, decreases

Reason — Atmospheric pressure decreases with altitude due to (1) decrease in height of air column, (2) decrease in density of air.

Question 14

Altimeter is used in an aircraft to measure :

1. atmospheric pressure
2. altitudes
3. speed
4. distance travelled

Answer

altitudes

Reason — An altimeter is an aneroid barometer, and it is used in aircraft to measure it's altitude.

Exercise 4(B) — Very Short Answer Type

Question 1

Write the numerical value of the atmospheric pressure on the surface of the earth in pascal.

Answer

The numerical value of the atmospheric pressure on the surface of the earth is 1.013 x 10⁵ pascal.

Question 2

What physical quantity is measured in torr? How is it related to the S.I. unit of the quantity?

Answer

The physical quantity measured in torr is atmospheric pressure.

1 torr = 133.28 Pa

Question 3

Name the physical quantity which is expressed in the unit 'atm'. State its value in pascal.

Answer

Pressure is expressed in the unit 'atm'.

Value of 1 atm in pascal is 1 x 10⁵.

Question 4

A partially inflated balloon is placed inside a bell jar connected to a vacuum pump. On creating vacuum inside the bell jar, balloon gets more inflated. How does the pressure change: increase, decrease or remains same, inside the (a) bell jar and (b) balloon ?

Answer

(a) On creating vacuum inside the bell jar, the pressure inside it decreases due to the absence of air.

(b) The pressure inside the balloon remains the same as the amount of air inside the balloon does not change. The reason balloon gets more inflated on creating vacuum inside the bell jar is that due to vacuum the air surrounding the balloon has been removed so the pressure surrounding the balloon has decreased. But the air inside the ballon keeps pushing at the same pressure causing the ballon to inflate further.

Question 5

What is the purpose of a barometer?

Answer

The barometer is used to measure atmospheric pressure.

Question 6

What is meant by the statement 'the atmospheric pressure at a place is 76 cm of Hg'? State it's value in Pa.

Answer

The statement 'the atmospheric pressure at a place is 76 cm of Hg' means that the atmospheric pressure at that place is equal to the pressure due to mercury column of height 76 cm .

The value of 76 cm of Hg = 1.013 x 10⁵ Pa.

Question 7(a)

How is the barometric height of a simple barometer affected if it's tube is pushed down into the trough of mercury?

Answer

If the tube is pushed down into the trough of mercury, the barometric height remains unaffected.

Question 7(b)

How is the barometric height of a simple barometer affected if it's tube is slightly tilted from vertical?

Answer

If the tube is slightly tilted from vertical, the barometric height remains unaffected.

Question 7(c)

How is the barometric height of a simple barometer affected if a drop of liquid is inserted inside the tube?

Answer

If a drop of liquid is inserted inside the tube, the barometric height decreases. Reason being, the drop of liquid will vapourize due to vacuum and exert pressure on the mercury column due to which the barometric height will decrease.

Question 8

State two uses of a barometer.

Answer

The uses of a barometer are—

1. It can be used to measure the atmospheric pressure at a place.
2. It can be used as an altimeter to measure height.

Question 9

How is the height of mercury in a barometer affected when it is taken to (i) a mine, and (ii) a hill?

Answer

(a) When a barometer is taken to a mine, it's reading increases because the atmospheric pressure increases with depth.

(b) When a barometer is taken to a hill, it's reading decreases because atmospheric pressure decreases with increase in altitude.

Question 10

What do the following indicate in a barometer regarding weather —

(a) gradual fall in the mercury level,

(b) sudden fall in the mercury level,

(c) gradual rise in the mercury level ?

Answer

(a) If the barometric height gradually falls, it indicates that the moisture is increasing i.e., there is a possibility of rain.

(b) If the barometric height at a height suddenly falls, it means that the pressure at that place has suddenly decreased which indicates the coming of a storm or cyclone.

(c) A gradual increase in the barometric height means that the moisture in air is decreasing. This indicates the coming of dry weather.

Exercise 4(B) — Short Answer Type

Question 1

What do you understand by the term atmospheric pressure ?

Answer

The thrust exerted per unit area on the earth's surface due to column of air, is called atmospheric pressure on the surface of earth.

Question 2

We do not feel uneasy even under the enormous pressure of atmosphere above as well as around us. Give a reason.

Answer

We do not feel uneasy even under the enormous pressure of atmosphere above as well as around us because the pressure of our blood balances it. The blood pressure is slightly above the atmospheric pressure.

However, at high altitude, the atmospheric pressure becomes less because the height of air column above that altitude is less than at the earth's surface. As a result, at high altitudes the blood pressure becomes much more than the atmospheric pressure and nose bleeding may occur due to excess blood pressure.

Question 3

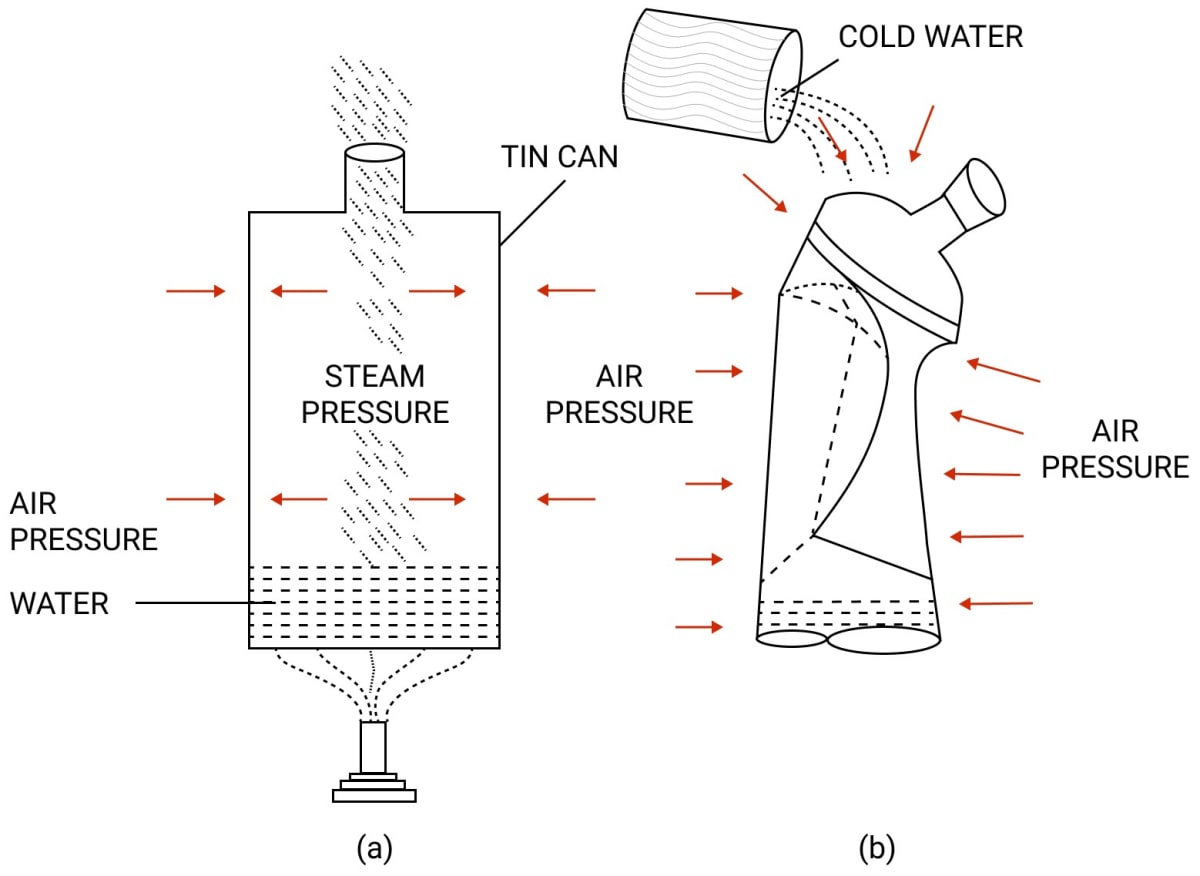
Describe an experiment to demonstrate that air exerts pressure.

Answer

We take a thin tin can fitted with an airtight stopper. The stopper is removed and a small quantity of water is boiled in the can.

Gradually, the steam occupies the entire space of can by expelling the air from it, as shown in figure below. The stopper is then tightly replaced and simultaneously the flame beneath the can is removed. Cold water is then poured over the can. It is observed that the can collapses inward, as shown below.

The reason is that, initially the pressure due to steam inside the heated can is same as the air pressure outside the can.

But, on pouring cold water over the can, fitted with a stopper the steam inside the can condenses, producing water and water vapour at a very low pressure. Now the air pressure outside the can exceeds the vapour pressure inside the closed can.

Consequently, the excess atmospheric pressure outside causes it to collapse it inwards. This demonstrates that the atmosphere outside the can exerts a pressure which is known as atmospheric pressure.

Question 4(i)

Explain the following:

A balloon collapses when air is removed from it.

Answer

A balloon collapses when air is removed from it because as the air is released from the balloon, the pressure inside the balloon is much less than the atmospheric pressure, hence, the balloon collapses.

Question 4(ii)

Explain the following:

Water does not run out of a dropper unless it's rubber bulb is pressed.

Answer

Water does not run out of a dropper unless it's rubber bulb is pressed because the pressure inside the dropper is same as the atmospheric pressure when the rubber bulb is not pressed. But, when we press the rubber bulb the pressure inside the dropper increases and hence the water flows out.

Question 4(iii)

Explain the following:

Two holes are made in a completely filled sealed tin can to take out oil from it.

Answer

Two holes are made in a completely filled sealed tin can to take out oil from it because there is no air inside a completely filled and sealed oil can. When the can is tilted, the pressure due to the column of oil (inside the can) at the hole is much less than the atmospheric pressure outside the can, so the oil does not flow out of the hole.

But if one more hole is made at the opposite end on the top cover of the can, air from outside the can will enter in through this hole and will exert atmospheric pressure on the oil from inside along with pressure due to oil column.

This results in the increase in the pressure on oil, and so it easily flows out through the hole of the can.

Question 5

Why does the liquid rise in a syringe when it's piston is pulled up ?

Answer

The syringe is kept with it's opening just inside a liquid and the plunger is lowered till it's base. Now when the plunger is pulled up in the barrel (as shown in figure), there is no air inside and thus the pressure inside the barrel below the plunger is much less than the atmospheric pressure acting on the liquid surface. As a result, the atmospheric pressure forces the liquid to rise up in the syringe.

Question 6

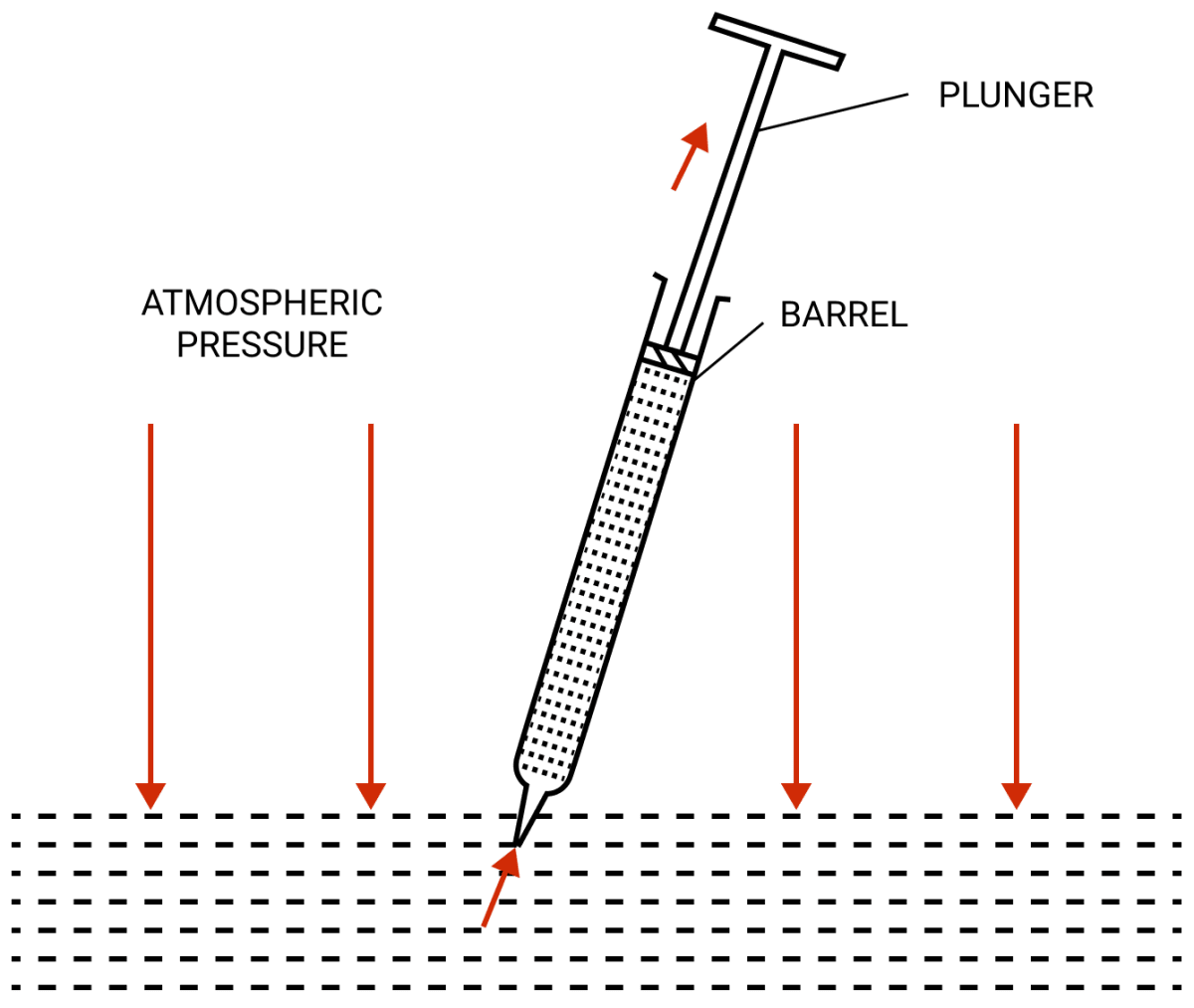
How is water drawn up from a well by a water pump?

Answer

In a water pump when the plunger is pulled up in the piston, there is no air inside and thus the pressure inside the siphon is much less than the atmospheric pressure acting on the liquid surface. As a result, the atmospheric pressure forces the water to rise up in the pump.

Question 7

Explain how is the height of mercury column in the tube of a simple barometer, a measure of the atmospheric pressure.

Answer

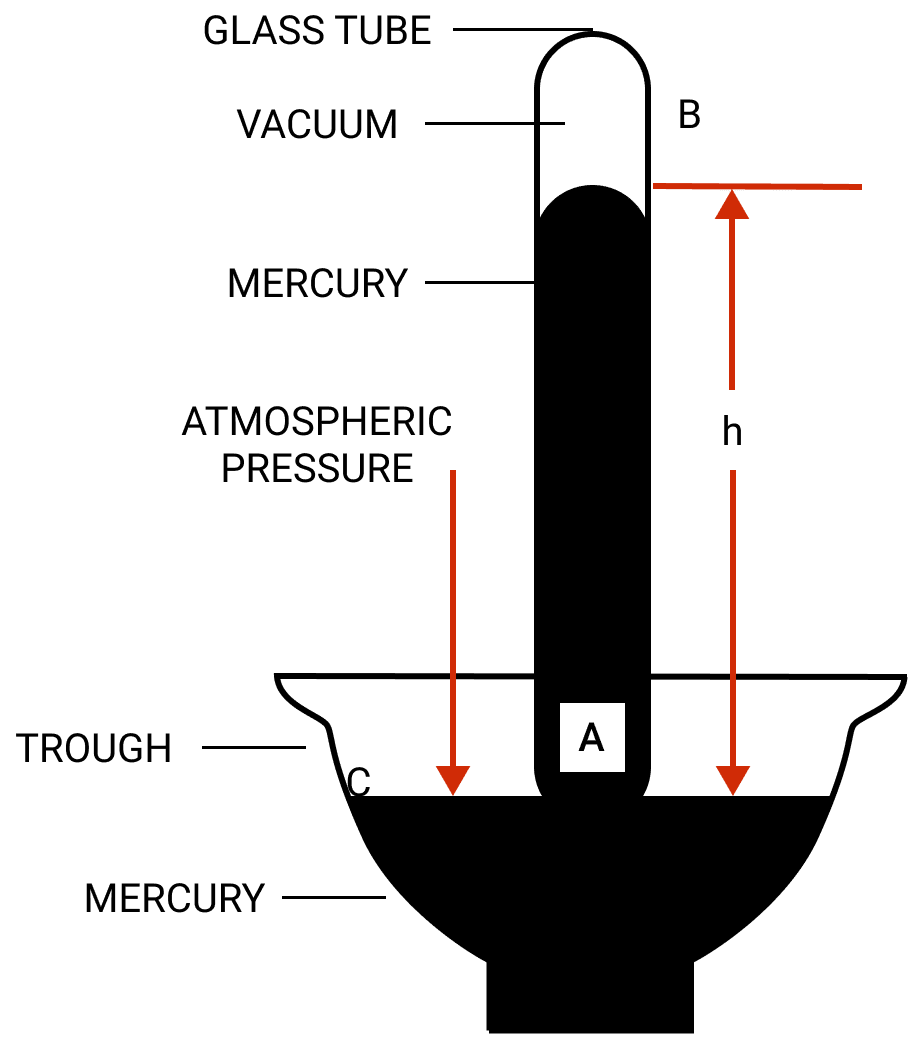
In figure, the atmospheric pressure acts at all points outside the tube (such as C) on the surface of mercury in the trough. The pressure at point A is due to the weight of the mercury column AB above it.

The mercury level in the tube becomes stationary when the pressure inside the tube at the point A which is at the level of the point C, becomes equal to that at the point C.

Thus, the vertical height of mercury column in it (i.e., AB = h) is a measure of atmospheric pressure and is called the barometric height.

The space left empty above the mercury column in the tube is called the torricellian vacuum. Ideally there should be no air in this space.

Question 8

Illustrate with the help of a labelled diagram of a simple barometer that the atmospheric pressure at a place is 76 cm of Hg.

Answer

Vertical height of the mercury column from the mercury surface in the trough to the level in tube, is a measure of the atmospheric pressure and the barometric height at normal temperature and pressure at sea level is 0.76 m ( or 76 cm or 760 mm) of mercury.

Question 9

Why is the barometric height used as a unit to express the atmospheric pressure ?

Answer

If the atmospheric pressure increases, the pressure at point C increases and mercury from trough flows into the tube thereby increasing the vertical height of mercury column in the tube so as to equalise pressures at points A and C.

On the other hand, when the atmospheric pressure decreases, the vertical height of the mercury column decreases to balance it.

Thus, the vertical height of the mercury column from the mercury surface in the trough to the level in the tube, is a measure of the atmospheric pressure.

Question 10

How will you show there is vacuum above the surface of mercury in a barometer? What name is given to this vacuum ?

Answer

In an accurate barometer, the empty space above the mercury in the tube is perfect vacuum. If somehow air enters the empty space or a drop of water (or liquid) gets into the tube, it will immediately change into vapour in the vacuum space and the air (or the vapours of liquid) will exert pressure on the mercury column due to which the barometric height will decrease.

Such a barometer is a faulty barometer and it's barometric height will be less than the actual atmospheric pressure.

The name given to this space is torricellian vacuum.

Question 11

Give two reasons for the use of mercury as a barometric liquid.

Answer

Uses of mercury as a barometric liquid are —

1. The vapour pressure of mercury is negligible, so the vapours in the torricellian vacuum does not affect the barometric height.
2. Mercury neither wets nor sticks to the glass tube, therefore it gives accurate reading.

Question 12

Give two reasons why water is not a suitable barometric liquid.

Answer

Water is not a suitable barometric liquid because —

1. The vapour pressure of water is high, so it's vapours in the vacuum space will make the reading inaccurate.
2. Water is transparent, so it's surface is not easily seen while taking the observation.

Question 13

State two advantages of an aneroid barometer over a simple barometer.

Answer

Advantages of an aneroid barometer over a simple barometer are —

(a) Aneroid barometer is calibrated directly to read the atmospheric pressure.

(b) It has no liquid and is portable.

Question 14

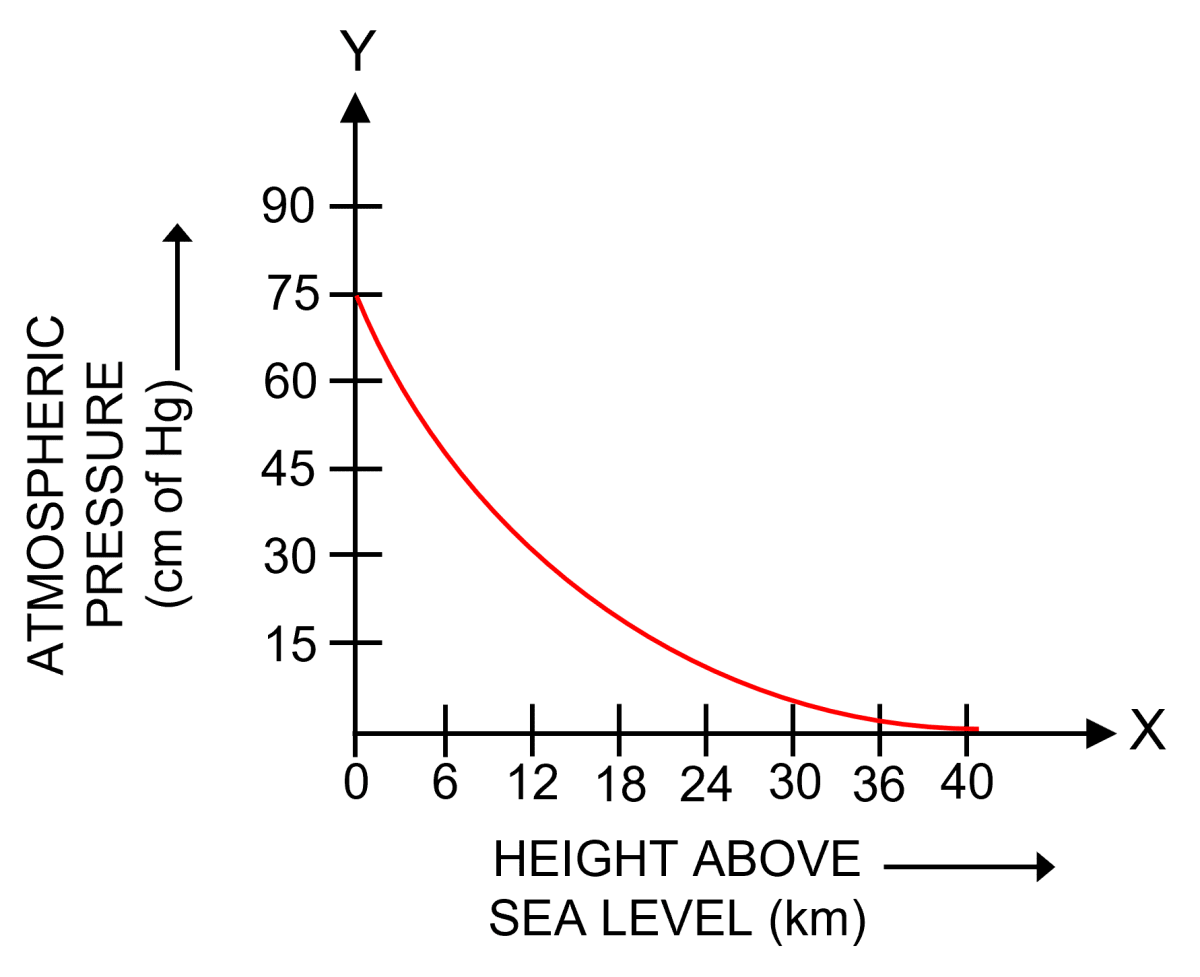
How does atmospheric pressure change with altitude ? Draw an approximate graph to show this variation.

Answer

The atmosphere consists of a number of parallel air layers. Each layer experiences a pressure on it due to the thrust or weight of the air column above it. Therefore, as we go up, the height of air column above us decreases and so thrust exerted by air column also decreases, which results in the decrease of atmospheric pressure with increases in altitude.

Since the lower air layers gets compressed due to the weight (or thrust) of the upper layers, therefore, the density of air layers is more near the earth's surface and it decreases as we go higher and higher.

The decrease in density with altitude is not linear. It is rapid at low altitude (near the sea level) and is slow at higher altitude. Due to decrease in density of air with altitude, the atmospheric pressure also decreases with altitude in a non linear way.

The figure below shows the variation of atmospheric pressure with height above the sea level.

Question 15

State two factors which affect the atmospheric pressure as we go up.

Answer

The atmospheric pressure decreases as we go up because —

1. Decrease in height of air colum which causes a linear decrease in the atmospheric pressure.
2. Decrease in density of air which causes a non-linear decrease in atmospheric pressure.

Question 16

Why does a fountain pen leak at a high altitude?

Answer

At high altitudes, a fountain pen leaks because normally a fountain pen filled with ink contains some air also which is at a pressure equal to the atmospheric pressure on the earths' surface. When the pen is taken at an altitude, the atmospheric pressure at this altitude is low so the excess pressure due to air inside the rubber tube forces the ink to leak out.

Question 17

Why does our nose start bleeding on high mountains?

Answer

Our blood pressure is slightly more than atmospheric pressure. However, at high altitude, the atmospheric pressure becomes less because the height of air column above that altitude is less than at the earth's surface. As a result, at high altitudes the blood pressure becomes much more than the atmospheric pressure and nose bleeding may occur due to excess blood pressure.

Exercise 4(B) — Long Answer Type

Question 1

What is a barometer? How is a simple barometer constructed?

Answer

A barometer is an instrument which is used to measure the atmospheric pressure.

A simple barometer uses mercury as the barometric liquid.

Construction — It uses a hard glass tube of about 1 m closed at one end. The tube is completely filled with pure mercury such that no air bubble remains inside the tube. The open end of tube is closed with thumb and the tube is then made upside down several times so as to force out any air bubble which might have entered in it.

The completely filled tube with it's open end closed by thumb is then inverted into a trough of mercury in such a way that the open end of tube is well immersed in mercury in a trough and the tube stands vertical as shown in figure. Now the thumb is removed. Care is taken that no air enters in the tube.

It is seen that the level of mercury in the tube falls till it's height above the level of mercury in the trough becomes h (nearly 76 cm) as shown in the diagram below.

Question 2

Mention two demerits of a simple barometer and state how they are removed in a Fortin barometer.

Answer

The demerits of a simple barometer are —

1. There is no protection for the glass tube.
2. A scale cannot be fixed with the tube to measure the atmospheric pressure.

Fortin barometer removes these demerits in the following ways:

1. The glass tube is protected by enclosing it in a brass case.
2. For accurate measurement, a main scale alongwith a vernier scale are provided.

Question 3

What is an altimeter? State it's principle. How is it's scale calibrated ?

Answer

An altimeter is an aneroid barometer, and it is used in aircraft to measure it's altitude.

It's principle is as follows —

As atmospheric pressure decreases with the increase in height above the sea level, therefore a barometer which measures the atmospheric pressure, can be used to determine the altitude of a place above the sea level.

It's scale is calibrated in terms of height of ascent with height increasing towards left because the atmospheric pressure decreases with increase of height above the sea level.

Question 4

Draw a simple labelled diagram of a Fortin barometer and state how it is used to measure the atmospheric pressure.

Answer

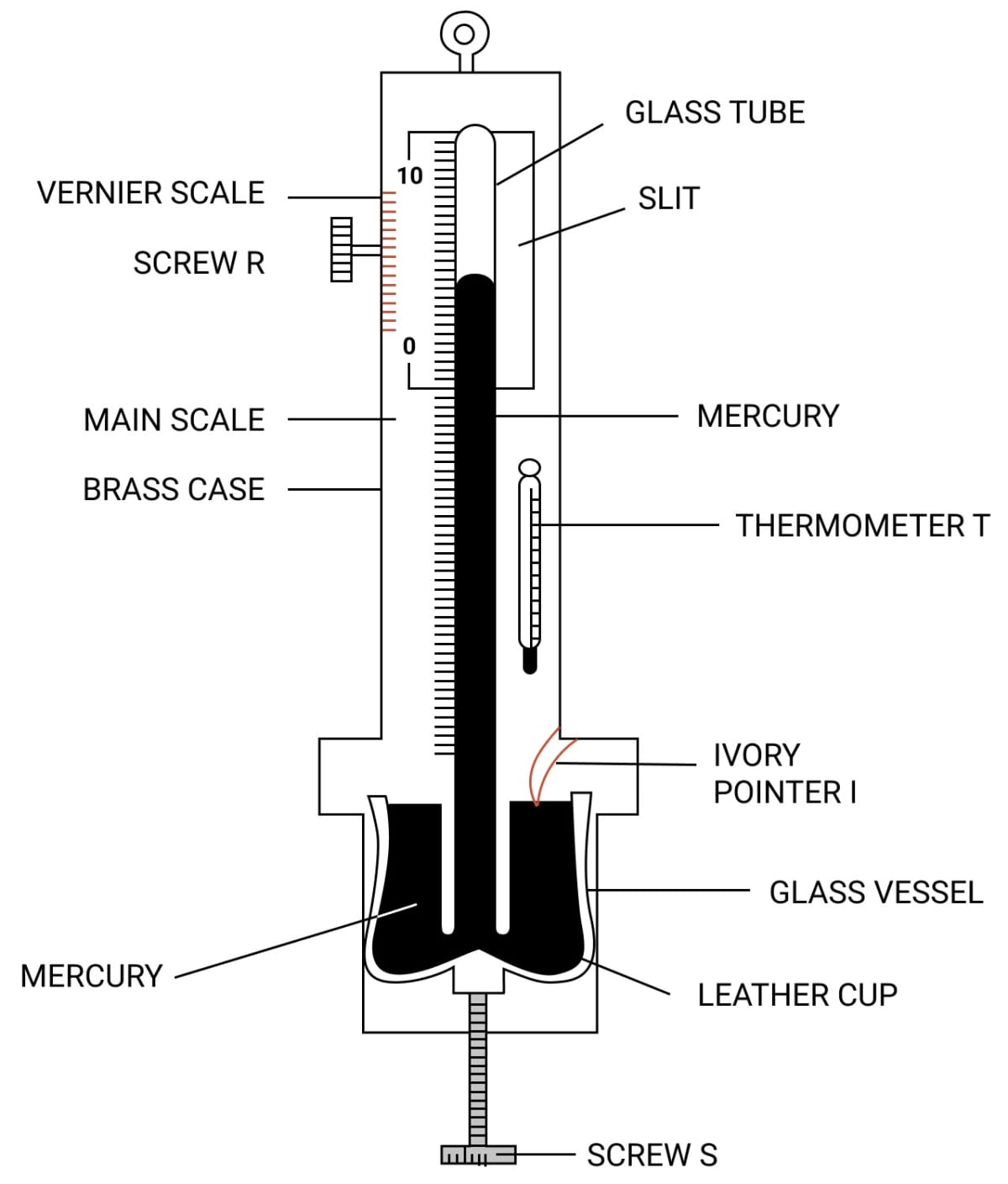
To measure the atmospheric pressure, first the mercury in the leather cup is raised up or lowered down with the help of the screw S so that the mercury level in the glass vessel just touches the ivory point I. The position of mercury level in the barometer tube is noted with the help of the main scale and the vernier scale. The sum of vernier scale reading and the main scale reading gives the barometric height. The barometric height shows the atmospheric pressure.

Question 5

What is an aneroid barometer? Draw a neat and labelled diagram to explain its construction and working.

Answer

Aneroid barometer has no liquid. It is light and portable. It is calibrated to read directly the atmospheric pressure.

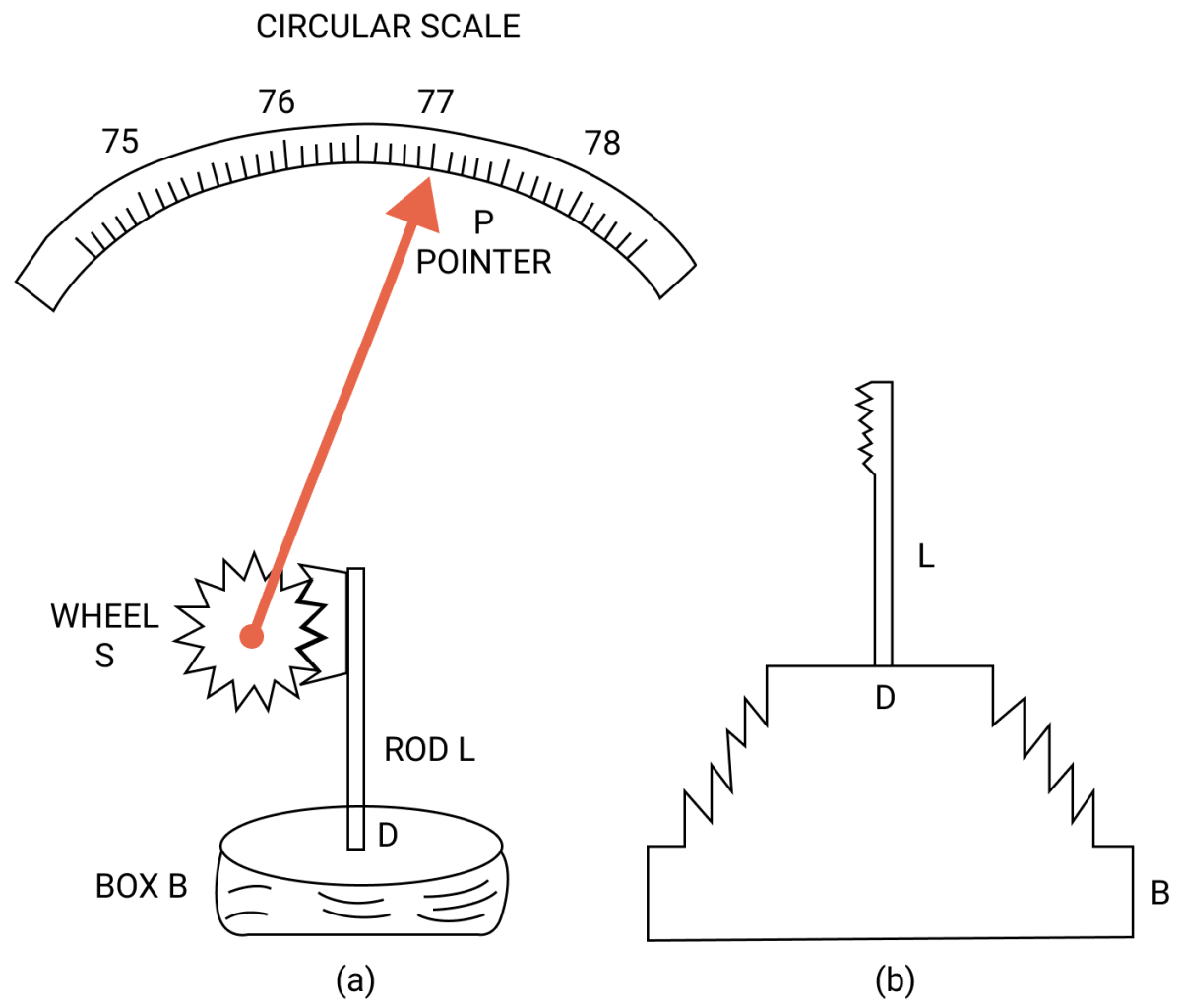
Construction —

The figure above shows the main parts of an aneroid barometer. It consists of a metallic box B which is partially evacuated. The top D of box is springy and is corrugated in form of a diaphragm as shown in fig (b).

At the middle of the diaphragm, there is a thin rod, toothed at it's upper end. The teeth of rod fit well into the teeth of a wheel S attached with a pointer P which can move over a circular scale.

The circular scale is graduated and is initially calibrated with a standard barometer so as to read the atmospheric pressure directly in terms of the barometric height.

Working —

When the atmospheric pressure increases, it presses the diaphragm D and the rod L gets depressed. The wheel S rotates clockwise and pointer P moves to the right on the circular scale.

On the other hand, when atmospheric pressure decreases, the diaphragm D bulges out due to which the rod L moves up and the wheel S rotates anticlockwise.

Consequently, the pointer shifts to the left and the pressure is read over the calibrated scale.

Exercise 4(B) — Numericals

Question 1

Convert 1 mm of Hg into pascal. Take density of Hg = 13.6 x 10³ kg m^-3 and g = 9.8 m s^-2

Answer

As we know,

Pressure = h ρ g

Given,

ρ = 13.6 10³ kg m^-3

g = 9.8 m s ^-2

h = 1 mm = 0.001 m (As 1 m = 1000 mm = 0.001 mm)

Substituting the values in the formula above we get,

$P = (0.001) \times (13.6 \times 10^{3}) \times (9.8) \\[0.5em] \Rightarrow P = 133.28 \text{ Pa} \\[0.5em]$

Hence, 1 mm of Hg = 133.28 Pa

Question 2

At a given place, a mercury barometer records a pressure of 0.70 m of Hg. What would be the height of water column if mercury in barometer is replaced by water ? Take density of mercury to be 13.6 x 10³ kg m^-3

Answer

We know that,

Pressure = h ρ g

Given,

ρ = 13.6 x 10³ kg m^-3

g = 9.8 m s ^-2

h = 0.70 m

Substituting the values in the formula above we get,

$P = (0.70) \times (13.6 \times 10^{3}) \times (9.8) \\[0.5em] \Rightarrow P = 93.3 \times 10^{3} \text { Pa} \\[0.5em]$

Hence, P = 93.3 x 10³Pa

Now, if we use a water barometer,

P = 93.3 x 10³ Pa

ρ = 1 x 10³ kg m^-3

g = 9.8 m s ^-2

Substituting the values in the formula above we get,

$93.3 \times 10^{3} = (h) \times (1 \times 10^{3}) \times (9.8) \\[0.5em] h = \dfrac{93.3 \times 10^{3}}{1 \times 10^{3} \times 9.8} \\[0.5em] h = 9.52 \text { m} \\[0.5em]$

Hence, height of water colum = 9.52 m

Question 3

At sea level, the atmospheric pressure is 76 cm of Hg. If air pressure falls by 10 mm of Hg per 120 m of ascent, what is the height of a hill where the barometer reads 70 cm of Hg. State the assumption made by you.

Answer

Given,

Atmospheric pressure = 76 cm of Hg

Change in pressure = 76 cm of Hg - 70 cm of Hg

= 6 cm of Hg

Pressure falls by 10 mm (= 1 cm) of Hg for every 120 m of ascent,

Therefore, for 6 cm of Hg we get,

$120 \times 6 = 720 m \\[0.5em]$

Hence, the height of the hill = 720 m

The assumption made is that the atmospheric pressure falls linearly with ascent.

Question 4

At sea level, the atmospheric pressure is 1.04 x 10⁵ Pa. Assuming g = 10 m s^-2 and density of air to be uniform and equal to 1.3 kg m^-3, find the height of the atmosphere.

Answer

We know that,

pressure = h ρ g

Given,

P = 1.04 x 10⁵ Pa

g = 10 m s^-2

density of air (ρ) = 1.3 kg m^-3

Substituting the values in the formula above, we get,

$1.04 \times 10^{5} = h \times 1.3 \times 10 \\[0.5em] h = \dfrac{1.04 \times 10^{5}}{1.3 \times 10} \\[0.5em] h = 8000 \text { m} \\[0.5em]$

Hence, height of the atmosphere = 8000 m

Question 5

Assuming the density of air to be 1.295 kg m^-3, find the fall in barometric height in mm of Hg at a height of 107 m above the sea level. Take density of mercury = 13.6 x 10³ kg m^-3

Answer

As we know,

decrease in pressure = h ρ g

Given,

density of air = 1.295 kg m^-3

h = 107 m

Therefore,

Decrease in pressure = (107) x (1.295) x (g)    [Equation 1]

Let, decrease in mercury height = H

Therefore, decrease in barometric height = (H) x (13.6 x 10³) x(g)   [Equation 2]

Equating 1 and 2 we get,

$107 \times 1.295 \times g = H \times 13.6 \times 10^{3} \times g \\[0.5em] \Rightarrow H = \dfrac{107 \times 1.295}{13.6 \times 10^{3}} \\[0.5em] \Rightarrow H = 0.0101 \text { m of Hg}$

Converting m into mm, we get

1 m = 1000 mm

Therefore, 0.0101 m = 0.0101 m x 1000 = 10.1 mm

Therefore, fall in barometric height = 10 mm of Hg.