Upthrust in Fluids, Archimedes' Principle and Floatation

Exercise 5(A) — Multiple Choice Type

Question 1

The property of a liquid to exert an upward force on a body immersed in it is called :

1. buoyancy
2. pressure
3. friction
4. viscosity

Answer

buoyancy

Reason — Buoyancy is defined as the property of a liquid to exert an upward force on a body immersed in it.

Question 2

If an empty can is pushed into water, we feel :

1. a downward force
2. an upward force
3. it is easy to push the can into water
4. both (a) and (c)

Answer

an upward force

Reason — The upward force exerted on the empty can by water opposing the push is called upthrust or buoyant force.

Question 3

The effect of upthrust is that the weight of a body immersed in a liquid appears to be :

1. more than its actual weight
2. the same as its weight outside the liquid
3. less than its actual weight
4. None of these

Answer

less than its actual weight

Reason — Due to the upthrust or the buoyant force acting on a body immersed in water, the weight of a body appears to be less than its actual weight.

Question 4

Which of the following are the correct characteristic properties of upthrust ?

(i) the smaller the volume of a body submerged in a liquid, the smaller is the upthrust

(ii) the upthrust acts on the body in an upward direction at the centre of buoyancy

(iii) for the same volume of a body inside a fluid, the less the density of the fluid, greater will be the upthrust

1. (i) & (ii)
2. (i) & (iii)
3. (ii) & (iii)
4. (i), (ii) & (iii)

Answer

(i) & (ii)

Reason — Characteristic properties of upthrust :

1. Larger the volume of a body submerged in a fluid, greater is the upthrust.
2. For the same volume of a body inside a fluid, more the density of fluid, greater is the upthrust.
3. The upthrust acts on the body in upward direction at the centre of buoyancy i.e., the centre of gravity of the displaced fluid.

Question 5

The S.I. unit of upthrust is:

1. Pa
2. N
3. kg
4. kg m²

Answer

N

Reason — Upthrust, being a force, has S.I. unit as newton (N).

Question 6

The correct relation for upthrust on a solid of volume V immersed in a liquid of density ρ is :

1. F_B = $\dfrac{\text{V}_{\text{s}}}{\text{g}}$

2. F_g = $\dfrac{\text{ρg}}{\text{V}}$

3. F_B = Vρg

4. F_g = $\dfrac{\text{V}_{\text{g}}}{\text{ρ}}$

Answer

F_B = Vρg

Reason —

Resultant upward thrust on the body

F_B = F₂ – F₂

= h₂ρgA - h₂ρgA

= A(h₂ - h₁)ρg

But, A(h₂ - h₁) = V, the volume of the body submerged in the liquid.

∴ Upthrust F_B = Vρg

Question 7

Archimedes' principle applies on :

1. solids and liquids
2. liquids and gases
3. solids and gases
4. solids, liquids and gases

Answer

liquids and gases

Reason — Archimedes' principle applies on both, liquids & gases.

Question 8

If a body is completely immersed in a liquid, the volume of the liquid displaced will be ............... its own volume and the upthrust will be ...............

1. less than, minimum
2. equal to, minimum
3. more than, maximum
4. equal to, maximum

Answer

equal to, maximum

Reason — If a body is completely immersed in a liquid, the volume of the liquid displaced will be equal to its own volume and the upthrust will be maximum.

Question 9

The apparent loss in weight is equal to the upthrust on the body verifies :

1. Pascal's law
2. Newton's third law
3. Archimedes' principle
4. Newton's second law

Answer

Archimedes' principle

Reason — Archimedes' principle states that when a body is immersed partially or completely in a liquid, it experiences an upthrust, which is equal to the weight of the liquid displaced by it.

Question 10

A body weighed 'W' in air by a sensitive spring balance, will weigh ............... in vacuum.

1. the same
2. slightly more
3. slightly less
4. zero

Answer

slightly more

Reason — A body weighed 'W' in air by a sensitive spring balance, will weigh slightly more in vacuum, because in vacuum no upthrust acts.

Question 11

Floating of a cork on the surface of water indicates that :

1. the density of water is more than the density of cork.
2. the density of water is less than the density of cork.
3. the density of water is equal to the density of cork.
4. the density of water plays no role in the floatation of cork.

Answer

the density of water is more than the density of cork.

Reason — Bodies of density greater than that of the liquid sink in it, while bodies of average density equal to or smaller than that of the liquid float on it.

Question 12

Sinking of an iron nail in water implies that :

1. the density of nail is more than the density of water
2. the density of nail is less than the density of water
3. the density of nail is equal to the density of water
4. the sinking of nail does not depend upon the density of water

Answer

the density of nail is more than the density of water

Reason — Bodies of density greater than that of the liquid sink in it, while bodies of average density equal to or smaller than that of the liquid float on it.

Question 13

Bodies of density ............... than that of the liquid sink in it, while bodies of average density equal to or ............... than that of the liquid float on it.

1. smaller, greater
2. greater, greater
3. greater, smaller
4. smaller, smaller

Answer

greater, smaller

Reason — Bodies of density greater than that of the liquid sink in it, while bodies of average density equal to or smaller than that of the liquid float on it.

Question 14

A body will experience minimum upthrust when it is completely immersed in:

1. Turpentine
2. Water
3. Glycerine
4. Mercury

Answer

Turpentine

Reason — One of the factors affecting the upthrust is the density of the liquid in which the body is submerged. Lesser the density of the liquid, lesser is the upthrust experienced by a body. As amongst the given options turpentine has the least density, hence minimum upthrust will be offered by turpentine.

Question 15

A body of density ρ sinks in a liquid of density ρ_L. The densities ρ and ρ_L are related as:

1. ρ = ρ_L
2. ρ < ρ_L
3. ρ > ρ_L
4. nothing can be said

Answer

ρ > ρ_L

Reason — Bodies of density greater than that of liquid, sink in it. Hence, ρ > ρ_L

Exercise 5(A) — Very Short Answer Type

Question 1

In what direction and at what point does the buoyant force on a body due to a liquid, act?

Answer

The buoyant force on a body due to a liquid acts in the upward direction at the center of buoyancy i.e. the centre of gravity of the displaced liquid.

Question 2

Define upthrust and state it's S.I. unit.

Answer

The upward force exerted on a body by the fluid in which it is submerged, is called the upthrust.

The S.I. unit of upthrust is Newton (N).

Question 3

Why is a force needed to keep a block of wood inside water?

Answer

A force is needed to keep a block of wood inside water because upthrust due to water on block when fully submerged is more than it's weight.

Question 4

A body experiences an upthrust F₁ in river water and F₂ in sea water when dipped up to the same level. Which is more F₁ or F₂ ? Give reason.

Answer

The upthrust in sea water (F₂) is more than the upthrust in river water (F₁). Hence, F₂ > F₁.

As we know that the sea water is denser than river water, and if the density of the liquid is more it exerts more buoyant force. Hence, the body in sea water will experience more upthrust than in river water.

Question 5

A body of volume V and density ρ is kept completely immersed in a liquid of density ρ_L . If g is the acceleration due to gravity, write expressions for the following —

(i) The weight of the body,

(ii) The upthrust on the body,

(iii) The apparent weight of the body in liquid,

(iv) The loss in weight of the body.

Answer

Given,

volume = V

density = ρ

density of liquid = ρ_L

acceleration due to gravity = g

(i) The weight of the body, acting downwards = V ρ g

(ii) The upthrust on the body, acting upwards = V ρ_L g

(iii) The apparent weight of the body in liquid = V(ρ - ρ_L)g

(iv) The loss in weight of the body = V ρ_L g

Question 6

Complete the following sentences —

(a) Two balls, one of iron and the other of aluminum experience the same upthrust when dipped completely in water if ............... .

(b) An empty tin container with it's mouth closed has an average density equal to that of a liquid. The container is taken 2m below the surface of that liquid and is left there. Then the container will ............... .

(c) A piece of wood is held under water. The upthrust on it will be ............... the weight of the wood piece.

Answer

(a) Two balls, one of iron and the other of aluminum experience the same upthrust when dipped completely in water if both have equal volumes.

(b) An empty tin container with it's mouth closed has an average density equal to that of a liquid. The container is taken 2m below the surface of that liquid and is left there. Then the container will remain at the same position.

(c) A piece of wood is held under water. The upthrust on it will be more than the weight of the wood piece.

Question 7

A sphere of iron and another of wood of the same radius are held under water. Compare the upthrust on the two spheres.

[Hint — Both have equal volume inside water.]

Answer

Let density of water be ρ_w

Since radius of both spheres are same hence their volume will be equal.
Let volume of iron sphere = volume of wood sphere = V

Upthrust on Iron sphere = Upthrust_iron = Vρ_wg

Upthrust on Wood sphere = Upthrust_wood = Vρ_wg

∵ Volume of iron sphere and volume of wood sphere is same hence, upthrust by water acting on both the spheres is same.

Comparing the upthrust on the two spheres:

$\dfrac{\text{Upthrust}_{\text{iron}}}{\text{Upthrust}_{\text{wood}}} = \dfrac{Vρ_wg}{Vρ_wg} \\[0.5em] \dfrac{\text{Upthrust}_{\text{iron}}}{\text{Upthrust}_{\text{wood}}} = \dfrac{1}{1}$

∴ Upthrust_iron : Upthrust_wood = 1 : 1

Question 8

A body of density ρ is immersed in a liquid of density ρ_L. State condition when the body will (i) float, (ii) sink, in liquid.

Answer

(i) When a body is immersed in a liquid such that density of the body is lower than or equal to the density of the liquid then it will float, (i.e.,when ρ ≤ ρ_L)

(ii) When a body is immersed in a liquid such that density of the body is greater than the density of the liquid then it will sink, (i.e., when ρ > ρL)

Question 9

State Archimedes' principle.

Answer

Archimedes' principle states that when a body is immersed partially or completely in a liquid, it experiences an upthrust, which is equal to the weight of the liquid displaced by it.

Exercise 5(A) — Short Answer Type

Question 1

What is meant by the term buoyancy?

Answer

The property of liquid to exert an upward force on a body immersed in it, is called buoyancy.

Question 2

What is the cause of upthrust? At which point it can be considered to act?

Answer

Upthrust or buoyant force arises due to the differences in pressure acting on the submerged object. The fluid exerts pressure on all sides of the object, and the pressure is greater at greater depths. The pressure difference between the top and bottom of an object creates an upward force (i.e., upthrust) that opposes the weight of the object.

Upthrust acts on the body in upward direction at the centre of buoyancy (i.e., the centre of gravity of the displaced liquid).

Question 3

State three characteristic properties of upthrust.

Answer

The upthrust has the following three characteristic properties:

1. Larger the volume of a body submerged in a fluid, greater is the upthrust.
2. For the same volume of a body inside a fluid, more the density of fluid, greater is the upthrust.
3. The upthrust acts on the body in upward direction at the centre of buoyancy i.e., the centre of gravity of the displaced fluid.

Question 4

A piece of wood if left under water, comes to the surface. Explain the reason.

Answer

When a piece of wood is left under water, two forces act on it, (i) it's weight (i.e., the force due to gravity) W which pulls it downwards, and (ii) the upthrust F_B due to water which pushes the wood upwards. The piece of wood comes to the surface because upthrust on the wood is more than the weight of the wood (i.e.,F_B > W ).

Question 5

Will a body weigh more in air or in vacuum when weighed with a spring balance? Give a reason for your answer.

Answer

A body weighs more in vacuum than in air when weighed with a spring balance because an upthrust acts on the body in air due to which it appears lighter than it's actual weight.

Question 6

A metal solid cylinder tied to a thread is hanging from the hook of a spring balance. The cylinder is gradually immersed into water contained in a jar. What changes do you expect in the readings of spring balance? Explain your answer.

Answer

When a metal solid cylinder tied to a thread, hanging from the hook of a spring balance is gradually immersed into water contained in a jar, then it is observed that the readings on the spring balance decrease.

This loss of weight is due to the upthrust (or buoyant force) of water on the cylinder, hence the reading decreases and the cylinder appears to be lighter.

Question 7

A body dipped into a liquid experiences an upthrust. State two factors on which upthrust on the body depends.

Answer

The factors on which upthrust on the body depends are —

1. Volume of the body immersed in the liquid (fluid), and
2. Density of the liquid (fluid) in which the body is submerged.

Question 8

How is the upthrust related to the volume of the body submerged in a liquid ?

Answer

Larger the volume of a body submerged in a fluid, greater is the upthrust.

Question 9

A bunch of feathers and a stone of the same mass are released simultaneously in air. Which will fall faster and why? How will your observation be different if they are released simultaneously in vacuum ?

Answer

When a bunch of feathers and a stone of same mass are allowed to fall in air, the stone falls faster than the bunch of feathers.

The reason is that upthrust due to air on stone is less than that on the bunch of feathers because the volume of stone is less than that of the bunch of feathers of same mass.

If they both are released simultaneously in vacuum, they will fall together because there will be no upthrust.

Question 10

A small block of wood is held completely immersed in (i) water, (ii) glycerine and then released. In each case, what do you observe ? Explain the difference in your observation in the two cases.

Answer

When we place a small block of wood in water and another identical block of wood in glycerine, we notice that both the blocks float but the volume of block immersed in glycerine is smaller as compared to the volume of block immersed in water.

The reason is that the density of glycerine is more than that of water and so it exerts more buoyant force and hence, less part of block is immersed.

Question 11

A sphere of iron and another of wood, both of same radius are placed on the surface of water. State which of the two will sink? Give reason to your answer.

Answer

When a sphere of iron and wood are placed in water then the sphere of iron will sink.

The reason is that ρ_iron > ρ_water, so the weight of iron sphere will be more than upthrust due to water on it. But ρ_wood < ρ_water, so sphere of wood will float will it's that much volume submerged inside water by which upthrust due to water on it balances it's weight.

Question 12

How does the density of material of a body determine whether it will float or sink in water?

Answer

The bodies of density greater than that of the liquid sink in it, while bodies of average density equal to or smaller than that of the liquid float on it.

Question 13

It is easier to lift a heavy stone under water than in air. Explain.

Answer

It is easier to lift a heavy stone under water than in air because due to the effect of upthrust, the stone experiences an upward buoyant force that balances the true weight of the stone which is acting in the opposite direction.

Hence, the weight of the stone immersed in water appears less than the actual weight.

Exercise 5(A) — Long Answer Type

Question 1

What do you understand by the term upthrust of a fluid? Describe an experiment to show its existence.

Answer

The upward force exerted on a body by the fluid in which it is submerged is called upthrust or buoyant force.

Experiment —

If a piece of cork is placed on a surface of water in a tub, it floats with nearly $\dfrac{2}{5}$ of it's volume inside the water. If the cork is pushed into the water and then released, it again comes to the surface of water and floats.

If the cork is kept immersed, our fingers experience some upward force. This upward force is the buoyant force.

Question 2

Describe an experiment to show that a body immersed in a liquid appears lighter than it really is.

Answer

The weight of body immersed in a liquid appears to be less than it's actual weight due to the effect of upthrust.

Experiment

Lifting of a bucket full of water from a well —

Take an empty bucket and tie a long rope to it. If the bucket is immersed in the water of a well keeping one end of rope in hand and the bucket is pulled when it is deep inside water, we notice that it is easy to pull the bucket as long as it is inside water.

But as soon it starts coming out of the water surface, it appears to become heavier and now more force is needed to lift it.

This experiment shows that the weight of body appears lighter when it is immersed in water than it's actual weight (in air).

Question 3

A body held completely immersed inside a liquid experiences two forces (i) F₁, the force due to gravity and (ii) F₂, the buoyant force. Draw a diagram showing the direction of these forces acting on the body and state the conditions when the body will float or sink.

Answer

Below diagram shows the direction of forces acting on a body completely immersed inside a liquid:

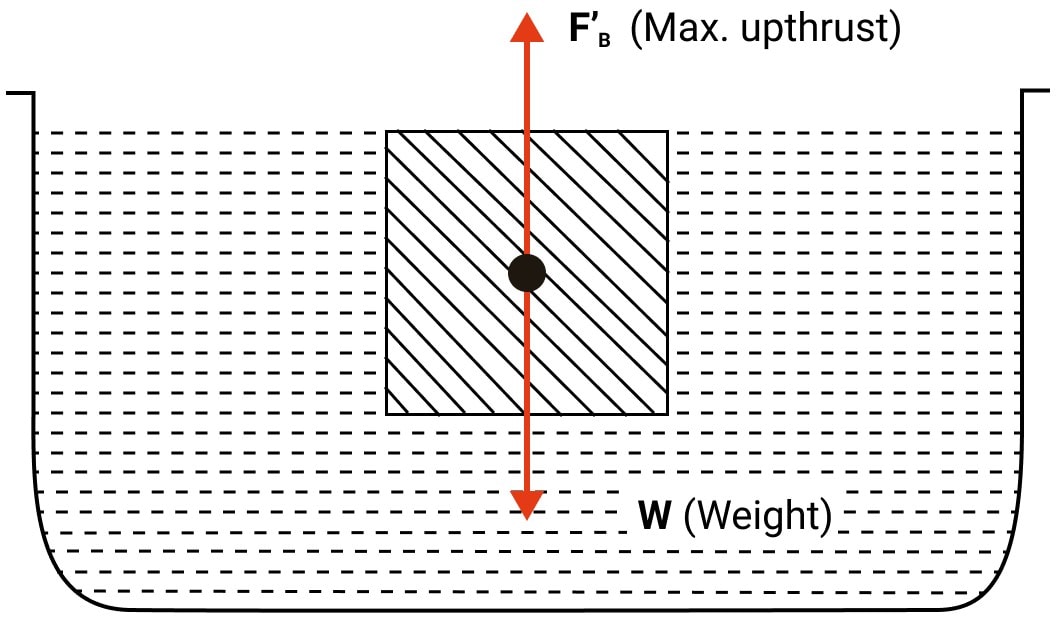
Whether the body will float or sink will depend on the relative values of F₁ and F₂.

(i) If F₁ <= F₂ then the body will float.

(ii) If F₁ > F₂ then the body will sink.

Question 4

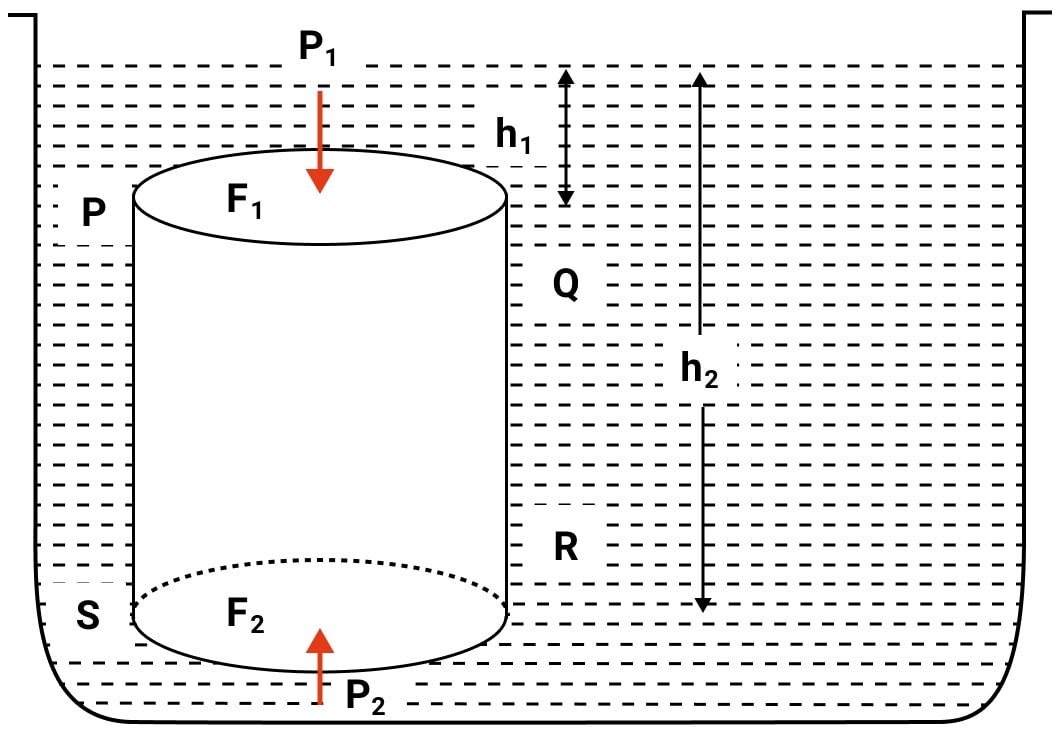
Prove that the loss in weight of a body when immersed wholly or partially in a liquid is equal to the buoyant force (or upthrust) and this loss is because of the difference in pressure exerted by liquid on the upper and lower surfaces of the submerged part of the body.

Answer

Consider a cylindrical body PQRS of cross-sectional area A immersed in a liquid of density ρ as shown in the figure. Let the upper surface PQ of body be at a depth h₁ while it's lower surface RS be at a depth h₂ below the free surface of liquid.

At depth h₁, the pressure on the upper surface PQ

P₁ = h₁ ρ g

∴ Downward thrust on the upper surface PQ

F₁ = pressure x area = h₁ ρ g A    [Equation 1]

At depth h₂, the pressure on the lower surface RS

P₂ = h₂ ρ g

∴ Upward thrust on the lower surface RS

F₂ = pressure x area = h₂ ρ g A    [Equation 2]

The horizontal thrust at various points on the vertical sides of the body get balanced because liquid pressure is same at all points at the same depth.

From above equations (1) and (2), it is clear that F₂ > F₁ as h₂ > h₁ and hence the body will experience a net upward force.

Resultant upward thrust on the body

F_B = F₂ – F₂

= h₂ρgA - h₂ρgA

= A(h₂ - h₁)ρg

But, A(h₂ - h₁) = V, the volume of the body submerged in the liquid.

∴ Upthrust F_B = Vρg

Vρg = Volume of solid immersed x density of liquid x acceleration due to gravity

Since a solid when immersed in a liquid, displaces liquid equal to the volume of its submerged part, therefore

Vρg = Volume of liquid displaced x density of liquid x acceleration due to gravity

= mass of liquid displaced x acceleration due to gravity

= weight of the liquid displaced by the submerged part of the body.

Hence,

Upthrust = weight of the liquid displaced by the submerged part of the body.

Now in another experiment, we suspend a solid by a thin thread attached to the hook of a spring balance to check its weight. Once the weight is noted, we fill a eureka can with water till its spout and place a measuring cylinder below the spout of the eureka can. The solid is then immersed in water and the displaced water is collected in the cylinder.

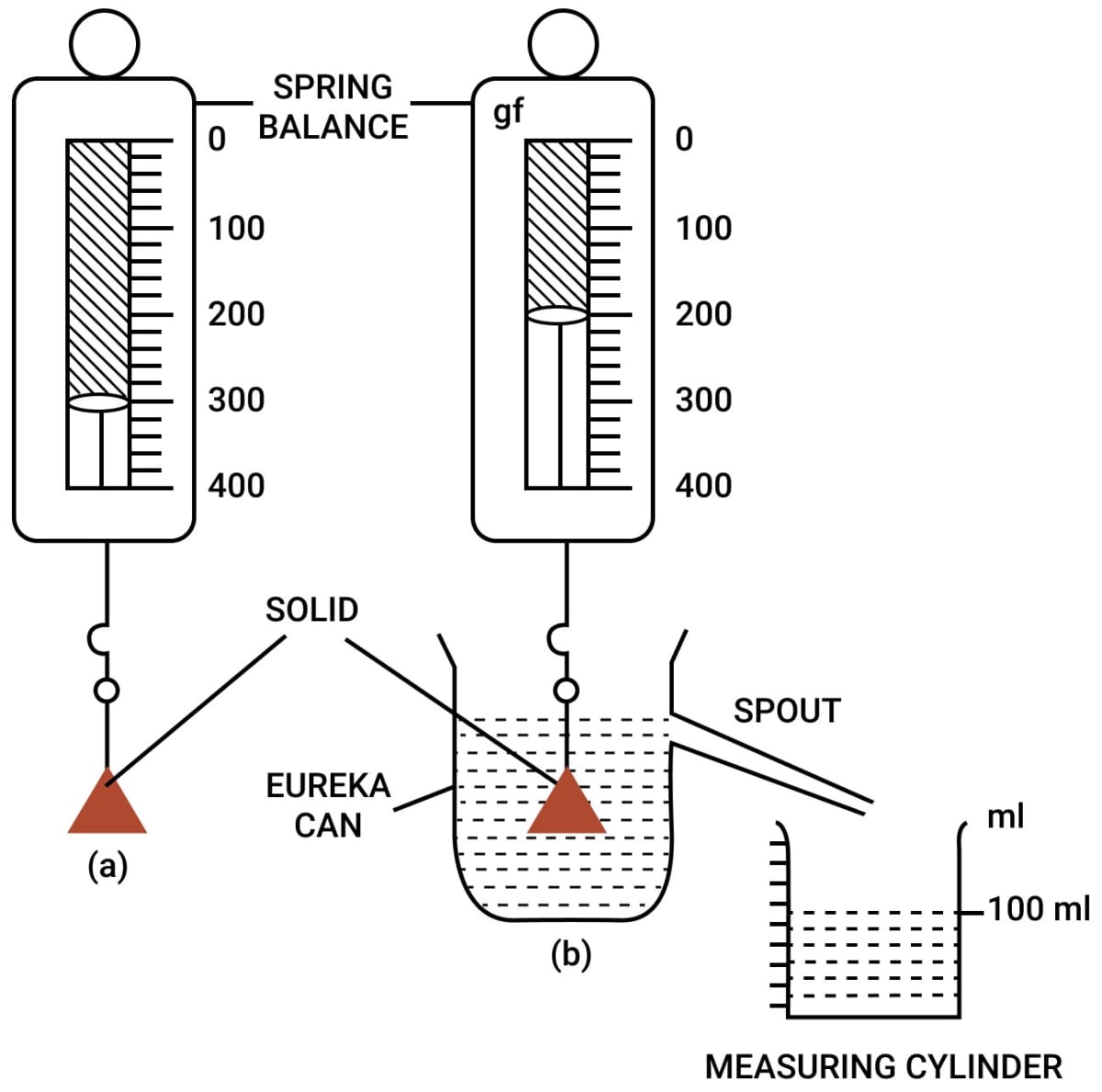
When the water stops dripping, the weight of the solid and the volume of water in the cylinder are noted.

In the above figure, the solid weighs 300 gf in air and 200 gf when it is completely immersed in water. The volume of water collected in the measuring cylinder is 100 ml i.e., 100 cm³

∴ Loss in weight = 300 gf - 200 gf = 100 gf   [Equation 1]

Volume of water displaced = Volume of solid = 100 cm³

∵ Density of water = 1 g cm^-3

∴ Weight of water displaced = 100 gf    [Equation 2]

From equations 1 and 2,

Weight of water displaced = Upthrust or loss in weight.

Thus, the weight of water displaced by a solid is equal to the loss in weight of solid.

Question 5

Describe an experiment to verify Archimedes' principle.

Answer

Experiment —

Take a solid (say a metallic piece). Suspend a solid by a thin thread from the hook of a spring balance. Note it's weight. Now take a eureka can and fill it with water to it's spout. Arrange a measuring cylinder below the spout of the eureka can.

Now, immerse the solid gently into water of the eureka can. The water displaced by it gets collected in the measuring cylinder, as shown in figure. When water stops dripping through the spout, note the weight of the solid and the volume of water collected in the measuring cylinder.

As shown in figure, the solid weighs 300 gf in air and 200 gf when it is completely immersed in water. The volume of water collected in the ,measuring cylinder is 100 ml i.e., 100 cm³.

Therefore, loss in weight = 300gf - 200gf = 100gf     [Equation 1]

Volume of water displaced = Volume of solid = 100 cm³

Since, density of water = 1 g cm^-3

Therefore, weight of water displaced = 100 gf    [Equation 2]

From eqns. (i) and (ii)

Weight of water displaced = Upthrust or loss in weight.

Thus, the weight of water displaced by a solid is equal to the loss in weight of the solid. This verifies Archimedes' principle.

Exercise 5(A) — Numericals

Question 1

A body of volume 100 cm³ weighs 5 kgf in air. It is completely immersed in a liquid of density 1.8 x 10³ kg m^-3. Find (i) the upthrust due to liquid and (ii) the weight of the body in liquid.

Answer

(i) As we know,

Upthrust due to liquid = volume of the solid x density of fluid x acceleration due to gravity

Given,

Volume of the body = 100 cm³

Converting cm³ into m³

100 cm = 1 m

So, 100 cm x 100 cm x 100 cm = 1 m³

Hence, 100 cm³ = $\dfrac{1 \times 100}{10,00,000}$

Therefore, V = 10^-4 m³

Weight of the body in air = 5 kgf

Density of the liquid = 1.8 x 10³ kg m^-3

Substituting the values in the formula above we get,

Upthrust = 10^-4 x 1.8 x 10³ x g = 0.18 kgf

Hence, the upthrust due to liquid = 0.18 kgf

(ii) weight of the body in liquid = weight of the body in air – upthrust

Substituting the values in the formula above, we get,

weight of the body in liquid = 5 kgf - 0.18 kgf = 4.82 kgf

Hence, weight of the body in liquid = 4.82 kgf

Question 2

A body weighs 450 gf in air and 310 gf when completely immersed in water.

Find —

(i) the volume of the body,

(ii) the loss in weight of the body, and

(iii) the upthrust on the body.

State the assumption made in part (i).

Answer

(i) Volume of the body = density of water x loss in weight

density of water = 1 g cm^-3

Given,

weight in air = 450 kgf

weight in water = 310 kgf

loss in weight = 450 – 310 = 140 gf

Substituting the values in the formula above, we get,

Volume of the body = 1 x 140 = 140 cm³

(ii) Loss in weight = 140 gf

(iii) Upthrust = loss in weight = 140 gf

Assumption in part (i) — density of water = 1.0 g cm^-3

Question 3

You are provided with a hollow iron ball A of volume 15 cm³ and mass 12 g and a solid iron ball B of mass 12 g. Both are placed on the surface of water contained in a large tub. (a) Find upthrust on each ball. (b) Which ball will sink ? Give reason for your answer. ( Density of iron = 8.0 g cm^-3)

Answer

(a) Upthrust due to liquid = volume of the solid x density of fluid x acceleration due to gravity   [Equation 1]

Volume = $\dfrac{\text {Mass}}{\text {density}}$   [Equation 2]

Given,

Mass of ball A = 12 g

Mass of ball B = 12 g

Volume of the hollow iron ball A = 15 cm³

Density of iron = 8 g cm³

Substituting the values in equation 2, to find volume of solid iron ball B,

Volume of solid iron ball B = $\dfrac{12}{8}$ = 1.5 cm³

Substituting the values in equation 1 to get upthrust on hollow ball A

Upthrust on hollow ball A = 15 x 1 x g = 15 gf

Hence, Upthrust on hollow ball A = 15 gf

Substituting the values in equation 1 to get upthrust on solid iron ball B

Upthrust on solid iron ball B = 1.5 x 1 x g = 1.5 gf

Hence, Upthrust on solid iron ball B = 1.5 gf

(b) Solid iron ball B will sink.
Ball B experiences an upthrust of 1.5 gf in water that is less than it's weight of 12 gf. Hence ball B will sink. Ball A experiences an upthrust of 15 gf that is greater than it's weight of 12 gf. Hence it will float with its that much part submerged for which upthrust becomes equal to its weight of 12 gf.

Question 4

A solid of density 5000 kg m^-3 weighs 0.5 kgf in air. It is completely immersed in water of density 1000 kg m^-3. Calculate the apparent weight of the solid in water.

Answer

(a) Upthrust = volume of the solid x density of fluid x acceleration due to gravity    [Equation 1]

and

Volume = $\dfrac{\text {Mass}}{\text {density}}$   [Equation 2]

Given,

Density of the solid = 5000 kg m^-3

Weight of the solid = 0.5 kgf

Density of water = 1000 kg m^-3

Substituting the values in equation 2 to get volume

Volume = $\dfrac{\text{0.5}}{\text{5000}}$ = 0.1 x 10^-3

Substituting the values in the formula above we get,

Upthrust = 0.1 x 10^-3 x 1000 x g = 0.1 kgf

apparent weight = true weight – upthrust

Substituting the values we get,

apparent weight = 0.5 - 0.1 = 0.4 kgf

Question 5

Two spheres A and B, each of volume 100 cm³ are placed on water (density = 1.0 g cm^-3). The sphere A is made of wood of density 0.3 g cm^-3 and the sphere B is made of iron of density 8.9 g cm^-3.

(a) Find (i) the weight of each sphere, and (ii) the upthrust on each sphere.

(b) Which sphere will float ? Give reason.

Answer

(a) Weight of sphere = volume of sphere x density of iron x g    [Equation 1]

Upthrust = volume of water displaced x density of water x g    [Equation 2]

Given,

Density of water = 1 g cm^-3

Density of sphere A = 0.3 g cm^-3

Density of sphere B = 8.9 g cm^-3

Volume of sphere A & B = 100 cm³

Substituting the values in the formula 1, we get weight of sphere A and B,

Weight of sphere A = 100 x 0.3 x g = 30 gf

Weight of sphere B = 100 x 8.9 x g = 890 gf

(ii) Substituting the values in the formula 2, we get upthrust on A and B,

Upthrust on sphere A = 100 x 1 x g = 100 gf

Upthrust on sphere B = 100 x 1 x g = 100 gf

(b) Sphere A will float.
The upthrust on sphere A is 100 gf which is more than its weight of 30 gf hence sphere A will float with its that much part submerged for which upthrust becomes equal to its weight of 30 gf. The upthrust on sphere B is also 100 gf but it is less than its weight of 890 gf hence sphere B will sink. In general, if the density of the body is less than the density of the liquid then it will float, and as the density of wood is lesser than the density of water hence sphere A floats.

Question 6

The mass of a block made of a certain material is 13.5 kg and it's volume is 15 x 10^-3 m³.

(a) Calculate upthrust on the block if it is held fully immersed in water.

(b) Will the block float or sink in water when released? Give reason for your answer.

(c) What will be the upthrust on block while floating? Take density of water = 1000 kg m^-3.

Answer

(a) Upthrust = volume of block x density of water x g

Given,

Mass of block = 13.5 kg

Volume of block = 15 x 10^-3 m³

Density of water = 1000 kg m^-3

Substituting the values in the formula above, we get, upthrust on block,

Upthrust on the block = 15 x 10^-3 x 1000 x g = 15 kgf

(b) The upthrust on the block when fully immersed is 15 kgf which is more than its weight of 13.5 kgf hence the block will float in water when released.

(c) The block will float with its that much part submerged for which upthrust becomes equal to its weight of 13.5 kgf. Hence while floating, upthrust on the block will be 13.5 kgf.

Question 7

A piece of brass weighs 175 gf in air and 150 gf when fully immersed in water. The density of water is 1.0 g cm^-3. (i) What is the volume of the brass piece? (ii) Why does the brass piece weigh less in water?

Answer

Given,

Weight of brass piece in air = 175 gf

Weight of the brass piece in water = 150 gf

Density of water = 1.0 g cm^-3

(i) Upthrust on brass piece = volume of brass piece x density of water x g

and

Upthrust on brass piece = Loss in weight = 175 gf - 150 gf = 25 gf

∴ 25 x g = volume of brass piece x density of water x g

⇒ 25 x g = volume of brass piece x 1 x g

⇒ volume of brass piece = 25 cm³

(ii) The brass piece weighs lesser in water due to the upthrust.

The brass piece experiences an upward buoyant force that balances the true weight of the piece which is acting in the opposite direction.

Hence, the weight of the brass piece immersed in water appears less than the actual weight.

Question 8

A metal cube of edge 5 cm and density 9.0 g cm^-3 is suspended by a thread so as to be completely immersed in a liquid of density 1.2 g cm^-3. Find the tension in thread. (Take g = 10 m s^-2)

[Hint: Tension in thread = apparent weight of the cube in liquid]

Answer

Given,

Edges of cube = 5 cm

∴ Volume = 5 x 5 x 5 = 125 cm³

Density of metal = 9.0 g cm^-3

Density of liquid = 1.2 g cm^-3

Mass of the cube = volume of the cube x density of the cube
= 125 x 9
= 1125 g

Upthrust on cube = volume of the cube x density of the liquid x g
= 125 x 1.2 x g
= 150 gf

Tension in thread = Apparent weight of the cube in liquid
= true weight – upthrust
= 1125 - 150
= 975 kgf
= 9.75 N    [∵ g = 10 ms^-2]

Hence, tension in thread = 9.75 N

Question 9

A block of wood is floating on water with it's dimensions 50 cm x 50 cm x 50 cm inside water. Calculate the buoyant force acting on the block. Take g = 9.8 N kg^-1.

Answer

Given,

g = 9.8 N kg^-1

density of water = 1000 kg m³

dimensions of wooden block = 50 cm x 50 cm x 50 cm
= 0.5 m x 0.5 m x 0.5 m    [converting to metres]

Volume of wooden block = 0.5 m x 0.5 m x 0.5 m = 0.125 m³

Buoyant force = volume of block x density of water x g
= 0.125 x 1000 x 9.8
= 1225 N

Question 10

A body of mass 3.5 kg displaces 1000 cm³ of water when fully immersed inside it. Calculate (i) the volume of body, (ii) the upthrust on body and (iii) the apparent weight of body in water.

Answer

Given,

Mass = 3.5 kg

Therefore, weight = 3.5 kgf

Volume of displaced water = 1000 cm³

(i) Volume of body = volume of the water displaced = 1000 cm³

Hence, the volume of body = 1000 cm³

(ii) Upthrust on body = volume of the body x density of water x g
= 1000 x 0.001 x g
= 1 kgf

(iii) The apparent weight of body in water = true weight – upthrust
= 3.5 - 1
= 2.5 kgf

Exercise 5(B) — Multiple Choice Type

Question 1

The effect of temperature on density is that it :

1. decreases with an increase in temperature
2. increases with an increase in temperature
3. first decreases then increases with a decrease in temperature
4. is not affected by temperature

Answer

decreases with an increase in temperature

Reason — Most of the substances expand on heating and contract on cooling, but their mass remains unchanged. Therefore, density of most of the substances decreases with the increase in temperature and increases with the decrease in temperature.

Question 2

The density of copper is :

1. 9.0 g cm^-3
2. 8.9 g cm^-3
3. 9.1 g cm^-3
4. 8.9 kg m^-3

Answer

8.9 g cm^-3

Reason — The density of copper is 8.9 g cm^-3. It means that the mass of 1 cm³ of copper is 8.9 g.

Question 3

The mass of 1 cm³ of iron is 7.8 g, its density in S.I. unit is :

1. 7.8 kg/cm³
2. 7.8 g cm^-3
3. 7800 g/cm³
4. 7800 kg/m³

Answer

7800 kg/m³

Reason —

Density = $\dfrac{\text{mass}}{\text{volume}}$ = $\dfrac{7.8}{1}$ g/cm³

Converting g cm^-3 into kg m^-3,

We know, 1 g = 10^-3 kg

1 cm = 10^-2 m

1 cm³ = 10^-6 m³

Therefore,

7.8 $\dfrac{\text {g}}{\text {cm}^3}$

= 7.8 $\dfrac{10^{-3}\text {kg}}{10^{-6} \text{m}^3}$

= 7.8 $\dfrac{10^{3}\text {kg}}{1 \text{m}^3}$

= 7.8 x 1000 kg m^-3

Hence,

7.8 g/cm³ = 7800 kg/m³

Question 4

The density of water is maximum at ............... °C and is ............... kg/m³

1. 0, 1
2. 0, 1000
3. 4, 1
4. 4, 1000

Answer

4, 1000

Reason — Due to anomalous expansion of water, when cooled it first contracts in volume but below 4°C, it starts expanding and continues to do so till the temperature reaches 0°C, the point at which it freezes into ice. Thus, The density of water is maximum at 4°C and is 1000 kg/m³.

Question 5

Relative density of a substance is expressed by comparing the density of that substance with the density of:

1. air
2. mercury
3. water
4. iron

Answer

Water

Reason — Relative density of a substance is also defined as the ratio of the mass of a certain volume of a substance to the mass of an equal volume of water at 4°C.

Question 6

The unit of relative density is:

1. g cm^-3
2. kg m^-3
3. m³ kg^-1
4. no unit

Answer

no unit

Reason — Since relative density is a pure ratio, it has no unit.

Question 7

The correct relation between density and relative density is :

1. R.D. = $\dfrac{\text{Density of substance in g cm}^{-3}}{1.0{\text{ g cm}^{-3}}}$

2. R.D. = $\dfrac{\text{Density of substance in g m}^{-3}}{1.0{\text{ g/cm}^{3}}}$

3. R.D. = $\dfrac{\text{Density of substance in kg cm}^{-3}}{1.0{\text{ g cm}^{3}}}$

4. None of these

Answer

R.D. = $\dfrac{\text{Density of substance in g cm}^{-3}}{1.0{\text{ g cm}^{-3}}}$

Reason — In C.G.S. system, density of water at 4°C is 1 g cm^-3, so the relative density of a substance is equal to the numerical value of density of that substance.

Thus, R.D. = $\dfrac{\text{Density of substance in g cm}^{-3}}{1.0{\text{ g cm}^{-3}}}$

Question 8

The relative density of silver is :

1. 11.7
2. 9.5
3. 12.8
4. 10.5

Answer

10.5

Reason — The relative density of silver is 10.5. It means that the mass of a certain volume of silver is 10.5 times the mass of an equal volume of water at 4°C.

Question 9

The correct expression for relative density when the weight of a body in air is W₁, and in water is W₂ is given by :

1. R.D. = $\dfrac{\text{W}_2}{\text{W}_1 - \text{W}_2}$

2. R.D. = $\dfrac{\text{W}_1}{\text{W}_1 + \text{W}_2}$

3. R.D. = $\dfrac{\text{W}_1 + \text{W}_2}{\text{W}_1}$

4. R.D. = $\dfrac{\text{W}_1}{\text{W}_1 - \text{W}_2}$

Answer

R.D. = $\dfrac{\text{W}_1}{\text{W}_1 - \text{W}_2}$

Reason — R.D. = $\dfrac{\text{Weight of body}}{\text{Weight of water displaced by the same body}}$

= $\dfrac{\text{Weight of body}}{\text{Loss of weight of body in water (or upthrust)}}$

$\dfrac{\text{Weight of body in air (W)}_1}{\text{Weight of body in air (W)}_1 - \text{Weight of body in water (W)}_2}$

Thus,

R.D. = $\dfrac{\text{W}_1}{\text{W}_1 - \text{W}_2}$

Question 10

If the weight of a body in air is W₁, in a liquid is W₂ and in water is W₃, then :

1. R.D. of liquid = $\dfrac{\text{W}_2 - \text{W}_3}{\text{W}_1 - \text{W}_3}$

2. R.D. of liquid = $\dfrac{\text{W}_1 - \text{W}_2}{\text{W}_1 - \text{W}_3}$

3. R.D. of liquid = $\dfrac{\text{W}_2 - \text{W}_3}{\text{W}_1 + \text{W}_3}$

4. R.D. of liquid = $\dfrac{\text{W}_1 - \text{W}_2}{\text{W}_1 + \text{W}_3}$

Answer

R.D. of liquid = $\dfrac{\text{W}_1 - \text{W}_2}{\text{W}_1 - \text{W}_3}$

Reason — R.D. of liquid = $\dfrac{\text{Weight of liquid displaced by a body}}{\text{Weight of water displaced by the same body}}$

R.D. of liquid = $\dfrac{\text{Weight of body in air (W)}_1 - \text{Weight of body in liquid (W)}_2}{\text{Weight of body in air (W)}_1 - \text{Weight of body in water (W)}_3}$

Thus,

R.D. of liquid = $\dfrac{\text{W}_1 - \text{W}_2}{\text{W}_1 - \text{W}_3}$

Exercise 5(B) — Very Short Answer Type

Question 1

Define the term density.

Answer

The density of a substance is it's mass per unit volume. i.e.,

$\text{Density} =\dfrac{\text {Mass of the substance}}{\text {Volume of the substance}}$

It is a scalar quantity and is represented by the letter ρ (rho) or d.

Question 2

What are the units of density in (i) C.G.S. and (ii) S.I. system.

Answer

(i) In C.G.S system, unit of density is g cm^-3.

(ii) In S.I. system, unit of density is kg m^-3.

Question 3

Express the relationship between the C.G.S. and S.I. units of density.

Answer

Relation between S.I. and C.G.S. units —

1 kg m^-3 = $\dfrac{1 \text {kg}}{1 \text {m}^{3}}$ = $\dfrac{1000 \text{g}}{(100 \text {cm})^{3}}$ = $\dfrac{{1}}{1000}$ g cm^-3

Thus,

1 kg m^-3 = 10^-3 g cm^-3 or

1 g cm^-3 = 1000 kg m^-3

Question 4

The density of iron is 7800 kg m^-3. What do you understand by this statement?

Answer

The statement tells that the mass of 1 m³ of iron is 7800 kg.

Question 5

Write the density of water at 4°C in S.I. unit.

Answer

The density of water at 4°C in S.I. unit is 1000 kg m^-3.

Question 6

How are the (i) mass, (ii) volume, and (iii) density of a metallic piece affected, if at all, with increase in temperature?

Answer

The parameters are affected in the following ways —

(i) Mass — It remains unchanged with increase in temperature.

(ii) Volume — It increases with an increase in the temperature.

(iii) Density — Most of the substances expand on heating and contract on cooling, but their mass remains unchanged. Therefore, density of most of the substances decreases with the increase in temperature.

Question 7

Complete the following sentences —

(i) Mass = .......... x density

(ii) S.I. unit of density is ..........

(iii) Density of water is .......... kg m^-3

(iv) Density in kg m^-3 = .......... x density in g cm^-3

Answer

(i) Mass = volume x density

(ii) S.I. unit of density is kg m^-3

(iii) Density of water is 1000 kg m^-3

(iv) Density in kg m^-3 = 1000 x density in g cm^-3

Question 8

What is the unit of relative density?

Answer

Relative density has no unit.

Question 9

A body weighs W gf in air and W₁ gf when it is completely immersed in water. Find (i) volume of the body, (ii) upthrust on the body, (iii) relative density of material of the body.

Answer

Given,

Weight of body in air = W

Weight of body in water = W₁

(i) Let V be the volume of the body.

Upthrust = loss in weight when immersed in water = (W - W₁) gf    ...[Eq 1]

Weight of water displaced = Volume of water displaced x density of water x g

Volume of water displaced = Volume of the body = V

Density of water = 1 g cm^-3

∴ Weight of water displaced = V x 1 x g = V gf     ...[Eq 2]

But weight of water displaced is equal to upthrust

∴ From eqns 1 & 2,

V = (W - W₁) cm³

∴ Volume of the body = V = (W - W₁) cm³

(ii) Upthrust = loss in weight when immersed in water = (W - W₁) gf

(iii) Relative density of the material of the body

= $\dfrac{\text {Weight of solid in air}}{\text {Weight in air - Weight in water}}$

= $\dfrac{W_1}{W_1 - W_2}$

Exercise 5(B) — Short Answer Type

Question 1

Water is heated from 0°C to 10°C. How does the density of water change with temperature?

Answer

On heating from 0°C, the density of water increases up to 4°C and then decreases beyond 4°C.

Question 2

What do you understand by the term relative density of a substance?

Answer

Relative density of a substance is defined as the ratio of the mass of a certain volume of a substance to the mass of an equal volume of water at 4°C.

Question 3

Define relative density as a ratio of mass?

Answer

Relative density is also defined as a ratio of mass of a certain volume of a substance to the mass of an equal volume of water at 4°C.

Question 4

Differentiate between density and relative density of a substance?

Answer

Exercise 5(B) — Long Answer Type

Question 1

With the use of Archimedes' principle, state how you will find relative density of a solid denser than water and insoluble in it. How will you modify your experiment if the solid is soluble in water?

Answer

Relative density of a solid denser than water and insoluble in it

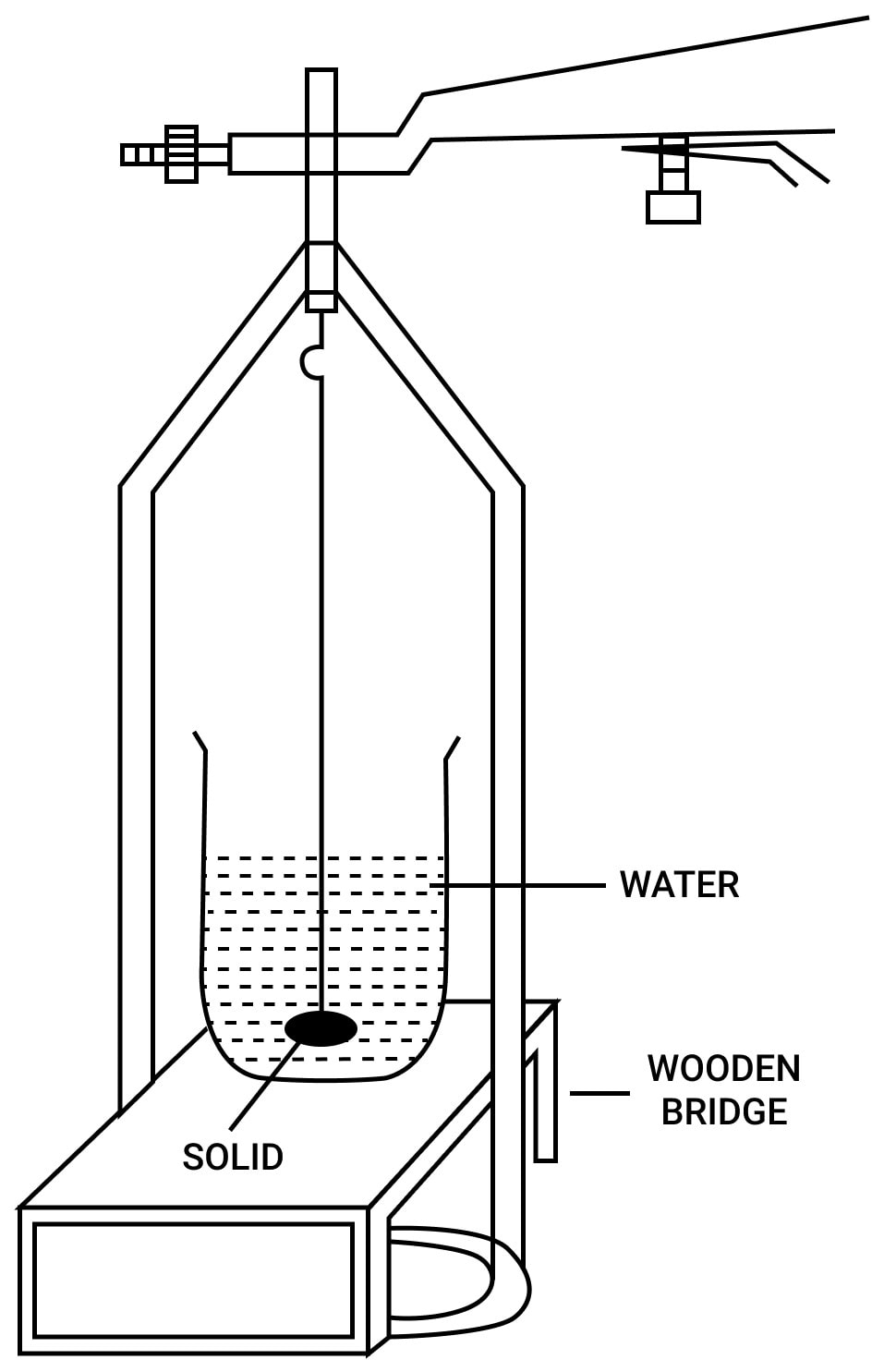
Procedure —

(i) Suspend a piece of the given solid with a thread from hook of the left pan of a physical balance and find it's weight W₁.

(ii) Now balance a wooden bridge over the left pan of balance and place a beaker nearly two-third filled with water on the bridge. Take care that the bridge and beaker do not touch the pan of balance,

(iii) Immerse the solid completely in water such that it does not touch the walls and bottom of beaker and find the weight W₂ of solid in water.

Observation —

Weight of solid in air = W₁ gf

Weight of solid in water= W₂ gf

Calculation —

Loss in weight of solid when immersed in water = (W₁ - W₂) gf

$\text{R.D.} = \dfrac{\text{ Weight of solid in air}}{\text{Loss in weight of solid in water}}$

or

$\text{R.D.} = \dfrac{W_{1}}{W_1 - W_2}$

Relative density of a solid denser than water and soluble in it —

Procedure —

If solid is soluble in water, instead of water, we take a liquid of known relative density in which solid in insoluble and it sinks in that liquid. Then the process described above is repeated. Now

$\text{R.D.} = \dfrac{\text{Wt of solid in air}}{\text{Loss in wt of solid in liq}} \times \text{R.D. of liq}$

Question 2

Describe an experiment, using Archimedes' principle, to find the relative density of a liquid.

Answer

By definition, relative density of a liquid is given as —

$\text{R.D.} = \dfrac{\text{Wt of given volume of liq}}{\text{Wt of same volume of water}}$

By Archimedes' Principle if a solid is immersed in a liquid or water, it displaces the liquid or water equal to it's volume. Therefore, above equation takes the form —

$\text{R.D.} = \dfrac{\text{Wt of liq displaced by body}}{\text{Wt of water displaced by body}} \\[0.5em] = \dfrac{(\text{Wt of body})_\text{air}-(\text{Wt of body})_\text{liq}}{(\text{Wt of body})_\text{air}-(\text{Wt of body})_\text{water}}$

Thus, to find the relative density of a liquid using Archimedes' Principle, we take a body which is heavier than both the given liquid and water and also insoluble in both. The body is first weighed in air, then in liquid and then after washing it with water and drying, it is weighed in water. If the weight of the body in air is W₁ gf, in liquid is W₂ gf and in water is W₃ gf, then from above we get,

$\text{R.D. of liquid} = \dfrac{W_1 - W_2}{W_1 - W_3}$

Question 3

A body weighs W₁ gf in air and when immersed in a liquid, it weighs W₂ gf, while it weighs W₃ gf on immersing it in water. Find: (i) volume of the body (ii) upthrust due to liquid (iii) relative density of the solid and (iv) relative density of the liquid.

Answer

Given,

Weight of the body in air = W₁ gf

Weight of the body in liquid = W₂ gf

Weight of the body in water = W₃ gf

(i) Let V be the volume of the body.

Upthrust due to water = loss in weight when immersed in water = (W₁ - W₃) gf    ...[Eq 1]

Weight of water displaced = Volume of water displaced x density of water x g

Volume of water displaced = Volume of the body = V

Density of water = 1 g cm^-3

∴ Weight of water displaced = V x 1 x g = V gf     ...[Eq 2]

But weight of water displaced is equal to upthrust due to water

∴ From eqns 1 & 2,

V = (W₁ - W₃) cm³

∴ Volume of the body = V = (W₁ - W₃) cm³

(ii) Upthrust due to liquid = loss in weight when immersed in liquid = (W₁ - W₂) gf

(iii) Relative density of the solid

$\text{R.D. of solid} \\[0.5em] = \dfrac{(\text{Wt of body})_\text{air}}{(\text{Wt of body})_\text{air}-(\text{Wt of body})_\text{water}} \\[0.5em] = \dfrac{W_1}{W_1 - W_3}$

(iv) Relative density of the liquid

$\text{R.D. of liquid} \\[0.5em] = \dfrac{(\text{Wt of body})_\text{air}-(\text{Wt of body})_\text{liquid}}{(\text{Wt of body})_\text{air}-(\text{Wt of body})_\text{water}} \\[0.5em] = \dfrac{W_1 - W_2}{W_1 - W_3}$

Exercise 5(B) — Numericals

Question 1

The density of copper is 8.83 g cm^-3. Express it in kg m^-3.

Answer

Converting g cm^-3 into kg m^-3,

We know, 1 g = 10^-3 kg

1 cm = 10^-2 m

1 cm³ = 10^-6 m³

Therefore,

8.83 $\dfrac{\text {g}}{\text {cm}^3}$

= 8.83 $\dfrac{10^{-3}\text {kg}}{10^{-6} \text{m}^3}$

= 8.83 $\dfrac{10^{3}\text {kg}}{1 \text{m}^3}$

= 8.83 x 1000 kg m^-3

Hence,

8.83 g cm^-3 = 8830 kg m^-3

Question 2

The relative density of mercury is 13.6. State it's density in (i) C.G.S. unit (ii) S.I. unit.

Answer

Given,

relative density of mercury = 13.6

(i) In C.G.S. unit,

R.D. = $\dfrac{\text {Density of substance in g cm}^{-3}}{\text{1.0 g cm}^{-3}}$

Substituting the values we get,

13.6 = $\dfrac{\text {Density of substance in g cm}^{-3}}{\text{1.0 g cm}^{-3}}$

Density of substance in g cm^-3 = (13.6) x (1.0) g cm^-3

Therefore,

Density of mercury in C.G.S. unit = 13.6 g cm^-3

(ii) In S.I. unit,

R.D. = $\dfrac{\text {Density of substance in kg m}^{-3}}{\text{1000 kg m}^{-3}}$

Substituting the values we get,

13.6 = $\dfrac{\text {Density of substance in kg m}^{-3}}{\text{1000 kg m}^{-3}}$

Density of substance in kg m^-3 = (13.6) x (1000) kg m^-3

Therefore,

Density of mercury in S.I. unit = 13.6 x 10³ kg m^-3

Question 3

The density of iron is 7.8 x 10³ kg m^-3. What is it's relative density ?

Answer

We know,

R.D. = $\dfrac{\text {Density of substance in kg m}^{-3}}{\text{1000 kg m}^{-3}}$

Given,

density of iron = 7.8 x 10³ kg m^-3

Substituting the values in the formula above we get,

R.D. = $\dfrac{7.8 \times 1000 \text { kg m}^{-3}}{\text{1000 kg m}^{-3}}$

Therefore,

Relative Density of iron = 7.8

Question 4

The relative density of silver is 10.8. Find its density.

Answer

We know,

R.D. = $\dfrac{\text {Density of substance in kg m}^{-3}}{\text{1000 kg m}^{-3}}$

Given,

relative density of silver = 10.8

Substituting the values in the formula above we get,

$10.8 = \dfrac{\text {Density of silver}}{\text{1000 kg m}^{-3}} \\[0.5em] \therefore \text {Density of silver} = (10.8 \times 1000) \text {kg m}^{-3}$

Question 5

Calculate the mass of a body whose volume is 2 m³ and relative density is 0.52.

Answer

As we know,

Mass = density x volume

Given,

volume = 2 m³

R.D. is 0.52

Now,

R.D. = $\dfrac{\text {Density of substance in kg m}^{-3}}{\text{1000 kg m}^{-3}}$

Substituting the values in the formula for R.D. we get,

0.52 = $\dfrac{\text {Density of body}}{\text{1000 kg m}^{-3}}$

Therefore,

Density of body = 0.52 x 10³ kg m^-3

Substituting the values in the formula for mass, we get,

$\text {Mass} = 0.52 \times 1000 \times 2 \\[0.5em] \Rightarrow \text {Mass} = 1040 \text {kg} \\[0.5em]$

Therefore, mass of body = 1040 kg

Question 6

Calculate the mass of air in a room of dimensions 4.5 m x 3.5 m x 2.5 m if the density of air at N.T.P. is 1.3 kg m^-3

Answer

Given,

Density of air = 1.3 kg m^-3

Dimensions of room = 4.5 m x 3.5 m x 2.5 m

∴ Volume of room = 4.5 x 3.5 x 2.5 = 39.375 m³

Mass = density x volume
= 1.3 x 39.375
= 51.1875 kg

Therefore, mass of body = 51.1875 kg ≈ 51.19 kg

Question 7

A piece of stone of mass 113 g sinks to the bottom in water contained in a measuring cylinder and water level in cylinder rises from 30 ml to 40 ml. Calculate R.D. of stone.

Answer

Given,

Mass of stone = 113 g

Rise in the level of water is equivalent to the volume occupied by the stone

Rise in water level = 40 ml – 30 ml = 10 ml

∴ Volume occupied by the stone = 10 cm³

$\text{Mass} = \text{Density} \times \text{Volume} \\[0.5em] \Rightarrow \text{Density} = \dfrac{\text{Mass}}{\text{Volume}} \\[0.5em] = \dfrac{113}{10} \\[0.5em] = 11.3 \text { g cm}^{-3}$

Therefore, density of stone = 11.3 g cm^-3

$\text{R.D. of stone} = \dfrac{\text {Density of stone in g cm}^{-3}}{\text{1.0 g cm}^{-3}} \\[0.5em] = \dfrac{11.3}{1} \\[0.5em] = 11.3$

Hence,

Relative density of stone = 11.3

Question 8

A body of volume 100 cm³ weighs 1 kgf in air. Find (i) it's weight in water and (ii) it's relative density.

Answer

Given,

Volume of body = 100 cm³

Weight of the body in air (W₁) = 1 kgf = 1000 gf

Let weight of the body in water be W₂

$\text{Density} = \dfrac{\text{Mass}}{\text{Volume}} \\[0.5em] = \dfrac{1000}{100} \\[0.5em] = 10 \text { g cm}^{-3}$

Hence,

Density of body = 10 g cm^-3

$\text{R.D. of body} = \dfrac{\text {Density of body in g cm}^{-3}}{\text{1.0 g cm}^{-3}} \\[0.5em] = \dfrac{10}{1} \\[0.5em] = 10$

Therefore,

Relative Density of body = 10

$\text{R.D. of body} = \dfrac{W_{1}}{W_{1} − W_{2}} \\[0.5em] \Rightarrow 10 = \dfrac{1000}{1000 − W_{2}} \\[0.5em] \Rightarrow 10 \times (1000 − W_{2}) = 1000 \\[0.5em] \Rightarrow 10000 - 10W_{2} = 1000 \\[0.5em] \Rightarrow 10W_{2} = 9000 \\[0.5em] \Rightarrow W_{2} = \dfrac{9000}{10} \\[0.5em] \Rightarrow W_{2} = 900 \text { gf}$

Hence,

(i) Weight in water = 900 gf

(ii) Relative density of body = 10

Question 9

A body of mass 70 kg, when completely immersed in water, displaces 20,000 cm³ of water. Find (i) the weight of body in water and (ii) the relative density of material of body.

Answer

Given,

Mass of body = 70 kg

Volume of water displaced = 20,000 cm³

Converting cm³ to m³, we get,

100 cm = 1m

100 cm x 100 cm x 100 cm = 1 m³

Therefore, 20,000 cm³ = $\dfrac{1}{10,00,000}$ x 20,000 = 0.02 m³

Hence, volume of water displaced = 0.02 m³

(i) Mass of body immersed in water = mass of the water displaced = volume of water displaced x density of water
= 0.02 x 1000
= 20 kg

Weight of the body = mg = 70 x g = 70 kgf

Weight of water displaced = mg = 20 x g = 20 kgf

Weight of body in water = weight of body in air - upthrust due to liquid
= 70 kgf - 20 kgf    [∵ upthrust is equal to weight of water displaced]
= 50 kgf

(ii) Formula for density is:

$\text{Density} = \dfrac{\text{Mass}}{\text{Volume}} \\[0.5em] = \dfrac{70}{0.02} \\[0.5em] = 3500 \text { Kg m}^{-3}$

$\text{R.D. of body} = \dfrac{\text {Density of body in kg m}^{-3}}{\text{1000 kg cm}^{-3}} \\[0.5em] = \dfrac{3500}{1000} \\[0.5em] = 3.5$

Therefore,

Relative density of body = 3.5

Question 10

A solid weighs 120 gf in air and 105 gf when it is completely immersed in water. Calculate the relative density of solid.

Answer

Given,

Weight of the solid in air (W₁) = 120 gf

Weight of the solid when completely immersed in water (W₂) = 105 gf

$\text{Relative density of solid} = \big(\dfrac{W_{1}}{W_{1} − W_{2}}\big) \\[0.5em] = \big(\dfrac{120}{120 - 105}\big) \\[0.5em] = 8$

∴ Relative density of solid = 8

Question 11

A solid weighs 32 gf in air and 28.8 gf in water. Find (i) the volume of solid, (ii) R.D. of solid, and (iii) the weight of solid in a liquid of density 0.9 g cm^-3.

Answer

Given,

Weight of the solid in air (W₁) = 32 gf

Weight of the solid immersed completely in water (W₂) = 28.8 gf

$\text{Relative density of solid} = \big(\dfrac{W_{1}}{W_{1} − W_{2}}\big) \\[0.5em] = \big(\dfrac{32}{32 - 28.8}\big) \\[0.5em] = \big(\dfrac{32}{3.2}\big) \\[0.5em] = 10 \\[1.5em] \text{But, R.D. of solid} = \dfrac{\text {Density of solid in g m}^{-3}}{\text{1 g cm}^{-3}} \\[0.5em] \Rightarrow 10 = \dfrac{\text {Density of solid in g m}^{-3}}{\text{1 g cm}^{-3}} \\[0.5em] \Rightarrow \text {Density of solid} = 10 \text{ g m}^{-3} \\[1.5em] \text{Density} = \dfrac{\text{Mass}}{\text{Volume}} \\[1em] \therefore \text{Volume} = \dfrac{\text{Mass}}{\text{Density}} \\[0.5em] = \dfrac{32}{10} \\[0.5em] = 3.2 \text { cm}^{3}$

Hence, volume of solid = 3.2 cm³

Let weight of solid in liquid of density 0.9 g cm^-3 be W.

$\text{R.D. of solid} = \Big(\dfrac{W_{1}}{W_{1} − W_{2}}\Big) \times \text{R.D. of liquid} \\[1em] \text{R.D. of liquid} = \dfrac{\text {Density of liquid in g cm}^{-3}}{\text{1.0 g cm}^{-3}} \\[0.5em] = \dfrac{0.9}{1} \\[0.5em] = 0.9$

Substituting the values in the formula for relative density of solid:

$10 = \Big(\dfrac{32}{32 − W}\Big) \times 0.9 \\[0.5em] 10 = \dfrac{28.8}{32 − W} \\[0.5em] 10 \times (32 - W) = 28.8 \\[0.5em] 320 - 10W = 28.8 \\[0.5em] 10W = 320 - 28.8 \\[0.5em] W = \dfrac{291.2}{10} \\[0.5em] W = 29.12 \text{ gf}$

Summarizing the answers:

(i) Volume of solid = 3.2 cm³

(ii) Relative density of solid = 10

(iii) Weight of solid in a liquid of density 0.9 g cm^-3 = 29.12 gf

Question 12

A body weighs 20 gf in air and 18 gf in water. Calculate relative density of the material of the body.

Answer

Given,

Weight of the solid in air (W₁) = 20 gf

Weight of the solid in water (W₂) = 18 gf

$\text{Relative density of body} = \big(\dfrac{W_{1}}{W_{1} − W_{2}}\big) \\[0.5em] = \big(\dfrac{20}{20 - 18}\big) \\[0.5em] = \big(\dfrac{20}{2}\big) \\[0.5em] = 10$

Question 13

A solid weighs 1.5 kgf in air and 0.9 kgf in a liquid of density 1.2 x 10³ kg m^-3. Calculate R.D. of solid.

Answer

Given,

Weight of the solid in air (W₁) = 1.5 kgf

Weight of the solid in liquid (W₂) = 0.9 kgf

Density of the liquid = 1.2 x 10³ kg m^-3

$\text{R.D. of liquid} = \dfrac{\text {Density of liquid in kg m}^{-3}}{\text{1000 kg cm}^{-3}} \\[0.5em] = \dfrac{1.2 \times 10^3}{1000} \\[0.5em] = 1.2$

$\text{R.D. of solid} = \Big(\dfrac{W_{1}}{W_{1} − W_{2}}\Big) \times \text{R.D. of liquid} \\[0.75em] = \Big(\dfrac{1.5}{1.5 - 0.9}\Big) \times 1.2 \\[0.75em] = \Big(\dfrac{1.5}{0.6}\Big) \times 1.2 \\[0.75em] = 3.0$

Question 14

A jeweller claims that he makes ornament of pure gold of relative density 19.3. He sells a bangle weighing 25.25 gf to a person. The clever customer weighs the bangle when immersed in water and finds that it weighs 23.075 gf in water. With the help of suitable calculations find out whether the ornament is made of pure gold or not.

[Hint — Calculate R.D of material of bangle which comes out to be 11.6]

Answer

Given,

Relative density of pure gold = 19.3

Weight of the bangle in air (W₁) = 25.25 gf

Weight of the bangle in water (W₂) = 23.075 gf

$\text{Relative density of bangle} = \big(\dfrac{W_{1}}{W_{1} − W_{2}}\big) \\[0.5em] = \big(\dfrac{25.25}{25.25 - 23.075}\big) \\[0.5em] = \big(\dfrac{25.25}{2.175}\big) \\[0.5em] = 11.6$

It is given that relative density of gold is 19.3 where as relative density of bangle is 11.6.

Hence, we can deduce that the bangle is not made of pure gold.

Question 15

A piece of iron weighs 44.5 gf in air. If the density of iron is 8.9 x 10³ kg m^-3, find the weight of the iron piece when immersed in water.

Answer

Given,

Weight of the solid in air (W₁) = 44.5 gf

Density of the iron = 8.9 x 10³ kg m^-3

$\text{R.D. of iron} = \dfrac{\text {Density of iron in kg m}^{-3}}{\text{1000 kg cm}^{-3}} \\[0.5em] = \dfrac{8.9 \times 10^3}{1000} \\[0.5em] = 8.9 \\[1.5em] \text{From relation, R.D.} = \dfrac{W_{1}}{W_{1} − W_{2}} \\[0.5em] \Rightarrow 8.9 = \dfrac{44.5}{44.5 - W_{2}} \\[0.5em] \Rightarrow 8.9 (44.5 - W_{2}) = 44.5 \\[0.5em] \Rightarrow (8.9 \times 44.5) - (8.9W_{2} ) = 44.5 \\[0.5em] \Rightarrow 396.05 - 8.9W_{2} = 44.5 \\[0.5em] \Rightarrow W_{2} = \dfrac{396.05 - 44.5}{8.9} \\[0.5em] \Rightarrow W_{2} = \dfrac{351.55}{8.9} \\[0.5em] \Rightarrow W_{2} = 39.5 \text{ gm} \\[0.5em]$

Hence,

Weight of iron piece when immersed in water = 39.5 gm

Question 16

A piece of stone of mass 15.1 g is first immersed in a liquid and it weighs 10.9 gf. Then on immersing the piece of stone in water, it weighs 9.7 gf. Calculate —

(a) the weight of the piece of stone in air,

(b) the volume of the piece of stone,

(c) the relative density of stone,

(d) the relative density of the liquid.

Answer

Given,

Mass of the stone = 15.1 g

(i) Weight = mass x acceleration due to gravity
= 15.1 x g
= 15.1 gf

Hence,

Weight of the piece of stone in air (W₁) = 15.1 gf

(ii) W₁ = 15.1 gf

Weight of the stone when immersed in water(W₃) = 9.7 gf

Upthrust on the stone = loss in weight when immersed in water

= Weight in air (W₁) - Weight in water (W₃)

= 15.1 – 9.7

= 5.4 gf

Let volume of the piece of stone be V.

From the relation, Upthrust on stone = volume of stone x density of water x acceleration due to gravity

5.4 x g = V x 1 x g
⇒ V = 5.4 cm³

∴ Volume of piece of stone = 5.4 cm³

(iii) From the relation,

$\text{Relative density of stone} = \big(\dfrac{W_{1}}{W_{1} − W_{3}}\big) \\[0.5em] = \big(\dfrac{15.1}{15.1 - 9.7}\big) \\[0.5em] = \big(\dfrac{15.1}{5.4}\big) \\[0.5em] = 2.79 \approx 2.8$

Hence,

Relative density of stone = 2.8

(iv) From the relation,

$\text{Relative density of liquid} = \dfrac{W_{1} - W_{2} }{W_{1} − W_{3}}$

where,

W₁ is the weight of piece of stone in air,
W₂ is the weight of piece of stone in liquid,
W₃ is the weight of piece of stone in water

Substituting the values in the formula above we get,

$\text{Relative density of liquid} = \dfrac{15.1 - 10.9}{15.1 - 9.7} \\[0.5em] = \dfrac{4.2}{5.4} \\[0.5em] = 0.777 \approx 0.78\\[0.5em]$

Hence,

the relative density of the liquid = 0.777 = 0.78

Exercise 5(C) — Multiple Choice Type

Question 1

For a floating body, its weight W and upthrust F_B on it are related as:

1. W > F_B
2. W < F_B
3. W = F_B
4. nothing can be said

Answer

W = F_B

Reason — When W = F_B i.e., the weight of the body is equal to the weight of the displaced liquid then the body will float.

Question 2

The upthrust is maximum (= F_B) when the body is:

1. floating in the liquid
2. completely immersed inside the liquid
3. partially immersed inside the liquid
4. None of these

Answer

completely immersed inside the liquid

Reason — As F_B = volume of submerged part of body x density of liquid x g

Hence, F_B will be maximum when the body is completely immersed inside the liquid.

Question 3

When the weight of a body is greater than the weight of the liquid displaced, the body will

1. float
2. sink
3. float partially outside
4. first go down then come up

Answer

sink

Reason — Two forces act on a body immersed in a liquid:

1. weight of the body acting vertically downwards and
2. upthrust acting vertically upwards.

Upthrust is equal in magnitude to the weight of the liquid displaced. When weight of a body is greater than the weight of the liquid displaced, implies downwards force is more than the upwards force, hence the body sinks.

Question 4

A body weighing W floats partially above and partially below the liquid when (F^'_B denotes maximum upthrust) :

1. W > F^'_B
2. W = F^'_B
3. W < F^'_B
4. none of these

Answer

W < F^'_B

Reason — When a body weighing W floats partially above and partially below the liquid, it implies that the weight of the body is less than the maximum upthrust experienced by it when fully immersed inside the liquid. Hence, W < F^'_B.

Question 5

A body of weight W is floating in a liquid. Its apparent weight will be:

1. equal to W
2. less than W
3. greater than W
4. zero

Answer

zero

Reason — When W = F_B i.e., the weight of the body is equal to the weight of the displaced liquid then the body will float and the apparent weight is equal to zero.

Question 6

For a floating body of volume V, the relation between the volume of its submerged part $v$, the densities of liquid (ρ_L) and the body (ρ_S) is :

1. $\dfrac{v}{V}$ = $\dfrac{ρ_s}{ρ_L}$

2. $\dfrac{V}{v}$ = $\dfrac{ρ_s}{ρ_L}$

3. $v \times ρ_s = V \times ρ_L$

4. none of these

Answer

$\dfrac{v}{V}$ = $\dfrac{ρ_s}{ρ_L}$

Reason —

Given,

Volume of body = V

Volume of body submerged in liquid = v

Density of body = ρ_s

Density of liquid = ρ_L

Let weight of the body be W. W = volume of the body x density of the body x g = V ρ_s g

Weight of liquid displaced by the body will be equal to upthrust. Let it be F_B.

F_B = volume of the liquid displaced x density of the liquid x g = v ρ_L g

From principle of floatation,

W = F_B

⇒ V ρ_s g = v ρ_L g

⇒ $\dfrac{v}{V}$ = $\dfrac{ρ_s}{ρ_L}$

Hence proved.

Question 7

A body floats in a liquid A of density ρ₁ with a part of it submerged inside liquid while in liquid B of density ρ₂ totally submerged inside liquid. The densities ρ₁ and ρ₂ are related as:

1. ρ₁ = ρ₂
2. ρ₁ < ρ₂
3. ρ₁ > ρ₂
4. nothing can be said

Answer

ρ₁ > ρ₂

Reason — Density of liquid A ( ρ₁) is greater than the density of liquid B ( ρ₂) as the body is partially immersed in liquid A whereas it is fully immersed in liquid B.

Question 8

Every ship has a white line painted on its side known as :

1. Plimsoll line
2. Border line
3. Harbour line
4. None of the above

Answer

Plimsoll line

Reason — Plimsoll line indicates the safe limit for loading the ship in water of density 10³ kg m^-3. A ship is not allowed to load further if its plimsoll line starts touching the water level, so that when it sails in sea water of density more than 10³ kg m^-3, only the part of it below the plimsoll line remains submerged in water.

Question 9

Which of the following statements is correct ?

(i) A loaded ship is submerged more while an unloaded ship is submerged less.

(ii) A ship begins to be less submerged as it sails from sea water to river water.

1. only (i)
2. only (ii)
3. both (i) and (ii)
4. both are incorrect

Answer

only (i)

Reason — A loaded ship is submerged more while an unloaded ship is submerged less because loaded ship has more weight and exerts more force vertically downwards.

A ship begins to be submerged more as it sails from sea water to river water. The water of a river is of low density than that of a sea. Therefore, a ship sails from sea water to river water, it sinks further. The reason is that according to the law of floatation, to balance the weight of ship, a greater volume of water is required to be displaced in water of lower density in river.

Question 10

An unloaded ship is filled with sand at its bottom to ............... its centre of gravity and make its equilibrium ...............

1. lower, unstable
2. higher, stable
3. lower, stable
4. higher, unstable

Answer

lower, stable

Reason — An unloaded ship floats with very small volume inside water. As a result, its centre of gravity is higher and its equilibrium is unstable. There is a danger that it may get blown over on its side by strong winds. Therefore, an unloaded ship is filled with sand (or stones), called ballast, at its bottom. This lowers its centre of gravity to make its equilibrium stable.

Question 11

It is easier for humans to swim in sea water than in river water as :

1. the density of sea water is less than that of the river water.
2. the density of sea water is more than that of river water.
3. the sea is big in comparison to the river.
4. None of the above

Answer

the density of sea water is more than that of river water

Reason — It is easier to swim in sea water because the density of sea water is more than that of the river water, so our weight is balanced in sea water with less part of the body submerged inside it.

Question 12

If a submarine is to dive, its ballast tanks are ..............., so that the average density of the submarine becomes ............... than the density of sea water.

1. filled with water, greater
2. filled with water, lower
3. emptied, greater
4. emptied, lower

Answer

filled with water, greater

Reason — If a submarine is to dive, its ballast tanks are, filled with water so that the average density of the submarine becomes greater than the density of sea water

Question 13

Ice bergs float on the surface of water with their ............... portion inside the water surface and ............... portion above the water surface.

1. smaller, larger
2. larger, equal
3. smaller, smaller
4. larger, smaller

Answer

larger, smaller

Reason — As ice bergs are lighter than water, they float on the surface of water with their larger portion inside the water surface and smaller portion above the water surface.

Question 14

A balloon does not rise indefinitely because :

1. the density of air increases with altitude
2. the density of air decreases with altitude
3. the weight of the displaced air increases.
4. None of the above

Answer

the density of air decreases with altitude

Reason — A balloon does not rise indefinitely because the density of air decreases with altitude. Therefore, as the balloon gradually goes up, the weight of the displaced air decreases. It keeps on rising as long as the upthrust on it exceeds its weight. When upthrust becomes equal to its weight, it stops rising further.

Question 15

When a fish has to rise up in water, it diffuses oxygen gas from its blood into the bladder, so its volume ............... and its average density ............... .

1. decreases, decreases
2. increases, decreases
3. decreases, increases
4. increases, increases

Answer

increases, decreases

Reason — When a fish has to rise up in water, it diffuses oxygen gas from its blood into the bladder, so its volume increases and its average density decreases

This increases the volume of water displaced by the fish and so the upthrust on the fish increases due to which it rises up.

Exercise 5(C) — Very Short Answer Type

Question 1

State the principle of floatation.

Answer

The principle of floatation states that the weight of a floating body is equal to the weight of the liquid displaced by it's submerged part.

Question 2

When a piece of wood is suspended from the hook of a spring balance, it reads 70 gf. The wood is now lowered into water. What reading do you expect on the scale of spring balance?

[Hint: The piece of wood will float on water and while floating, apparent weight = 0].

Answer

The piece of the wood will float on water and while floating, apparent weight is zero. Hence, the reading on the scale of spring balance will be zero.

Question 3

How does the density ρ_S of a substance determine whether a solid piece of that substance will float or sink in a given liquid of density ρ_L ?

Answer

The body will float if ρ_S ≤ ρ_L and it will sink if ρs > ρ_L

Question 4

A body floats in a liquid with a part of it submerged inside liquid. Is the weight of floating body greater than, equal to or less than upthrust?

Answer

When a body floats in a liquid then the weight of the floating body is equal to the upthrust.

Question 5

What can you say about the average density of a ship floating on water in relation to the density of water?

Answer

According to law of flotation, a body will float in a fluid if it has less density than the fluid. So, in order for the ship to float, its average density must be less than the density of water.

Question 6

Two identical pieces, one of ice (density = 900 kg m^-3) and other of wood (density = 300 kg m^-3) float on water.

(a) Which of the two will have more volume submerged inside water?

(b) Which of the two will experience more upthrust due to water?

Answer

(a) Ice will have more volume submerged inside water, because density of ice is more than the density of wood and we know that the body with higher density will have more volume submerged in water.

(b) Ice will have more volume submerged inside water and hence it will experience greater upthrust than the piece of wood. This is so because the upthrust is always equal to the volume of water displaced by the submerged part of the body and ice will displace more water than the piece of wood.

Question 7

A piece of ice floating in a glass of water melts, but the level of water in glass does not change. Give reason.

[Hint: Ice contracts on melting]

Answer

When a floating piece of ice melts into water, it contracts by the volume equal to the volume of ice piece above the water surface while floating on it. Hence, the level of water does not change when the ice floating on it melts.

Question 8

What can you say about the average density of a ship floating on water in relation to the density of water?

Answer

According to law of flotation, a body will float in a fluid if it has less density than the fluid. So, in order for the ship to float, its average density must be less than the density of water.

Question 9

A buoy is held inside water contained in a vessel by tying it with a thread to the base of the vessel. Name the three forces that keep the buoy in equilibrium and state the direction in which each force acts.

Answer

The three forces that keep the buoy in equilibrium are —

1. Weight of buoy acting in vertically downward direction.
2. Upthrust of water on buoy acting in vertically upward direction.
3. Tension in thread acting in vertically downward direction.

Question 10

A piece of ice floating in a glass of water melts, but the level of water in glass does not change. Give reason.

[Hint: Ice contracts on melting]

Answer

When a floating piece of ice melts into water, it contracts by the volume equal to the volume of ice piece above the water surface while floating on it. Hence, the level of water does not change when the ice floating on it melts.

Exercise 5(C) — Short Answer Type

Question 1

A solid iron ball of mass 500 g is dropped in mercury contained in a beaker. (a) Will the ball float or sink? Give reason. (b) What will be the apparent weight of ball? Give reason.

Answer

(a) When a solid iron ball of mass 500 g is dropped in mercury contained in a beaker, the ball will float because the density of iron ball is less than the density of mercury.

(b) The apparent weight of the ball is zero because while floating upthrust is equal to the weight of the body.

Question 2

Explain why an iron nail floats on mercury, but it sinks in water.

[Hint: Density of iron is less than that of mercury, but more than that of water]

Answer

Iron nail floats on mercury because the density of iron is less than that of mercury but it sinks in water because the density of iron is more than the density of water.

Question 3

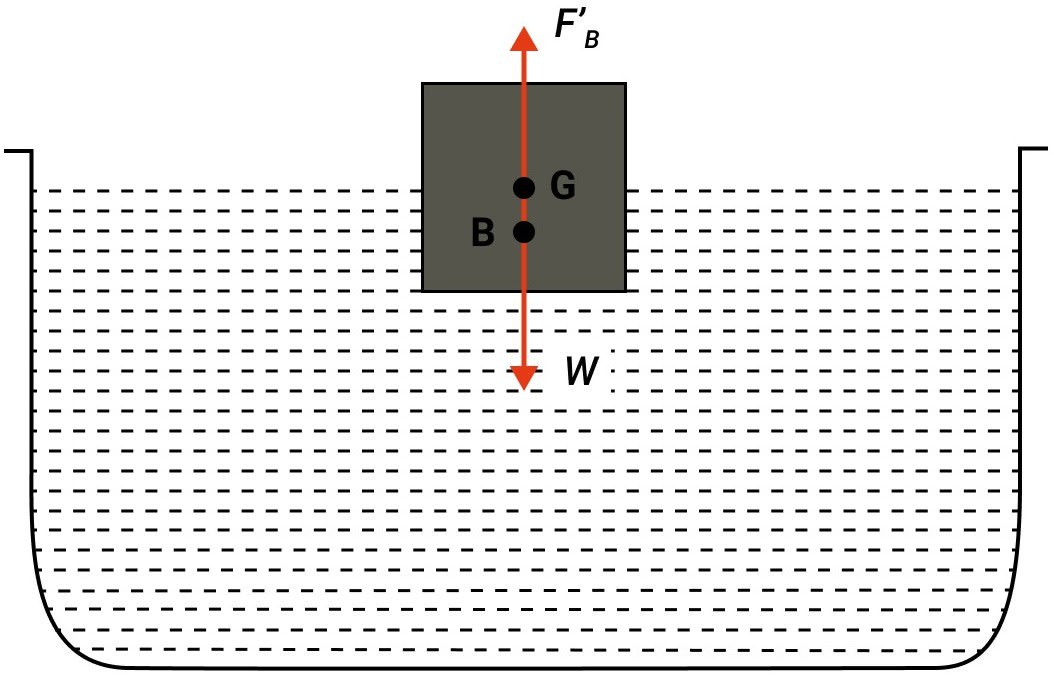
A homogenous block floats on water (a) partly immersed (b) completely immersed. In each case state the position of centre of buoyancy B with respect to the centre of gravity G of the block.

Answer

(a) When a homogenous block floats on water with it's body partly immersed then centre of buoyancy B will lie vertically below centre of gravity, G.

(b) When a homogenous block floats on water with it's body completely immersed then centre of buoyancy B will coincide with centre of gravity, G.

Question 4

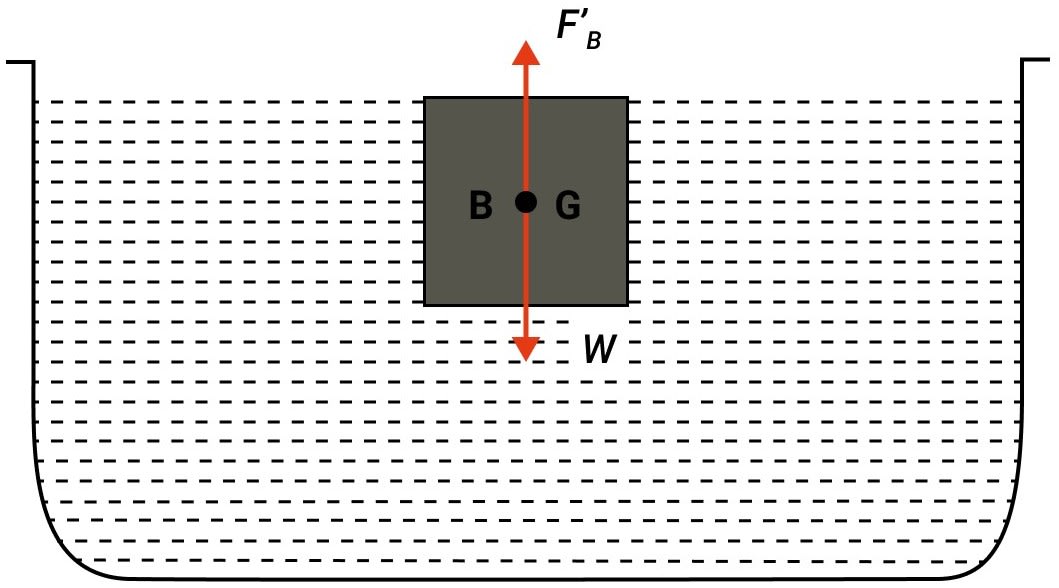
Figure shows the same block of wood floating in three different liquids A, B and C of densities ρ₁, ρ₂, and ρ₃ respectively. Which liquid has the highest density? Give reason for your answer.

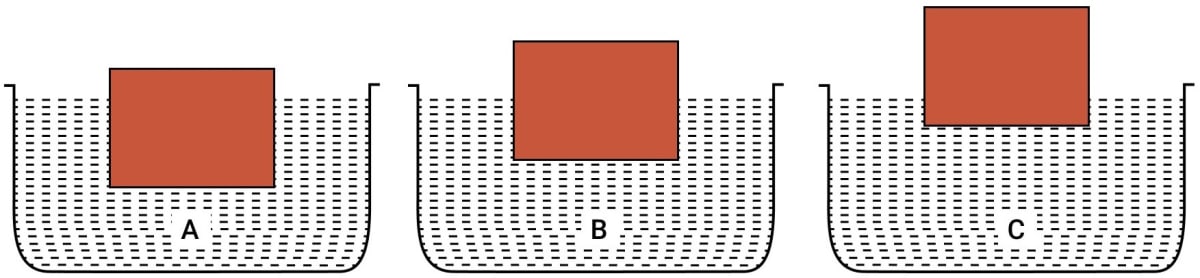
Answer

The liquid C has highest density.

The upthrust on the body by each liquid is the same and it is equal to the weight of body.

But. upthrust = volume submerged x ρ_L x g.

For liquid C, since volume submerged is least, so density ρ₃ must be maximum.

Question 5

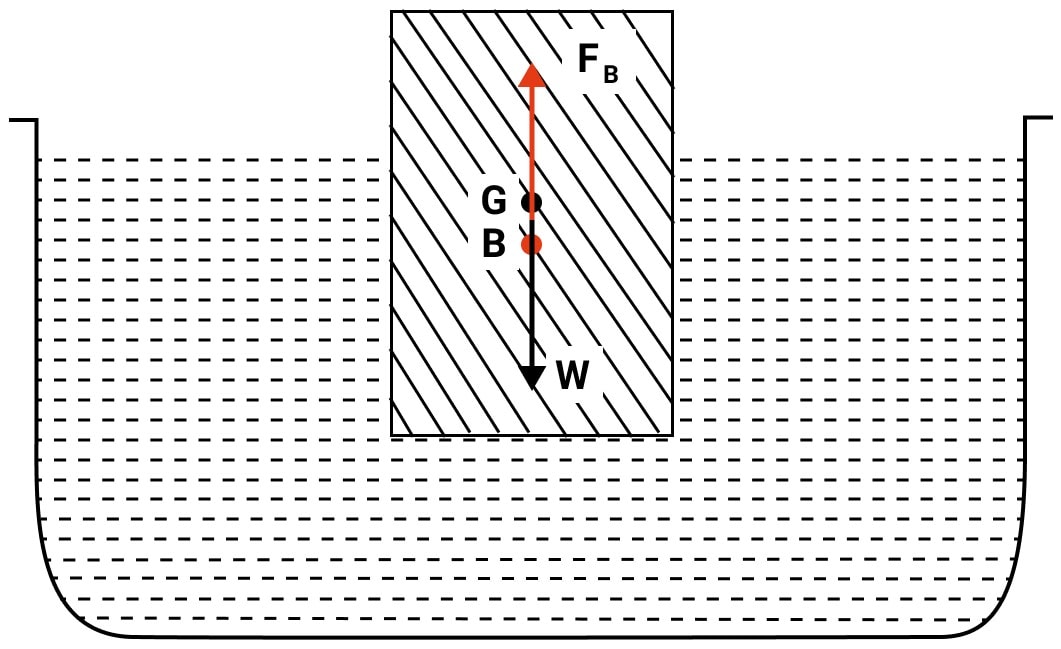
What is center of buoyancy? State it's position for a floating body with respect to the centre of gravity of body.

Answer

Centre of buoyancy B, is the centre of gravity of the displaced liquid.

The centre of buoyancy B, and centre of gravity G, will coincide if the body is fully immersed in the liquid.

In the case when the body is partially above and partially below the surface of liquid, the centre of buoyancy B is vertically below the centre of gravity G.

Question 6

A balloon filled with helium gas floats in a big closed jar which is connected to an evacuating pump. What will be your observation, if air from jar is pumped out? Explain your answer.

Answer

When air from jar is pumped out the balloon will sink.

As air from jar is pumped out, the density of air in jar decreases, so upthrust on balloon decreases, hence the weight of balloon exceeds the upthrust on it and the balloon sinks.

Question 7

A block of wood is so loaded that it just floats in water at room temperature. What change will occur in the state of floatation, if

(a) some salt is added to water,

(b) water is heated?

Answer

(a) The block floats with some part outside water when salt is added to the water.

On adding some salt to water, the density of water increases, so upthrust on block of wood increases and hence the block rises up till the weight of salty water displaced by the submerged part of the block becomes equal to the weight of block.

(b) When the water is heated, the block sinks.

On heating the water, the density of water decreases, so upthrust on block decreases and weight of block exceeds the upthrust due to which it sinks.

Question 8

Why is floating ice less submerged in brine than in water?

Answer

Floating ice is less submerged in brine than in water because the density of brine is more than the density of water.

Question 9

A man first swims in sea water and then in river water.

(i) Compare the weights of sea water and river water displaced by him.

(ii) Where does he find it easier to swim and why?

Answer

(i) In each case the weight of water displaced will be equal to the weight of the man.

Hence, the ratio weights of sea water and river water displaced by him will be 1:1.

(ii) The man finds it easier to swim in sea water because the density of sea water is more than that of the river water, so his weight is balanced in sea water with his less part submerged inside it.

Question 10

An iron nail sinks in water while an iron ship floats on water. Explain the reason.

Answer

An iron nail sinks in water because the density of iron is greater than the density of water, so the weight of the nail is more than the upthrust of water on it.

On the other hand, the ship is hollow and the empty space in it contains air which makes it volume large and average density less than that of water. Therefore, even with a small portion of ship submerged in water, the weight of water displaced by the submerged part of ship becomes equal to the total weight of ship and therefore, it floats.

Question 11

A loaded cargo ship sails from sea water to river water. State and explain your observation.

Answer

The ship begins to submerge more as it sails from sea water to river water.

The water of a river is of low density than that of a sea. Therefore, when a loaded cargo ship sails from sea water to river water, it sinks further. The reason is that according to the law of floatation, to balance the weight of ship, a greater volume of water is required to be displaced in water of lower density in river.

Exercise 5(C) — Long Answer Type

Question 1

A body is held immersed in a liquid. (i) Name the two forces acting on body and draw a diagram to show these forces. (ii) State how do the magnitudes of two forces mentioned in part (i) determine whether the body will float or sink in liquid when it is released. (iii) What is the net force on body if it (a) sinks, (b) floats?

Answer

(i) The two forces that act on the body immersed in liquid are —

1. The weight W of the body acting vertically downwards, through the centre of gravity G of the body. This force has a tendency to sink the body.

2. The upthrust F_B of the liquid acting vertically upwards, through the centre of buoyancy B i.e., the centre of gravity of the displaced liquid. This force has a tendency to make the body float.

(ii) Depending upon whether the maximum upthrust F'_B is less than, equal to or greater than the weight W, the body will either sink or float in liquid.

1. When W > F'_B i.e., the weight of the body is greater than the weight of the displaced liquid then the body will sink.
2. When W = F'_B i.e., the weight of the body is equal to the weight of the displaced liquid then the body will float just below the surface of liquid.
3. When W < F'_B i.e., the weight of the body is less than the weight of the displaced liquid the body will float partially submerged in the liquid. Only that much portion of the body gets submerged by which the weight of displaced liquid becomes equal to the weight of the body.

(iii) The net force on the body if it sinks/floats is as follows:

1. In the case when the body sinks, the net force acting on the body is the weight of the body itself.
2. In the case when the body floats, the net force acting on the body is the upthrust due to the liquid.

Question 2

Draw a diagram to show the forces acting on a body floating in water with it's some part submerged. Name the forces and show their points of application. How is the weight of water displaced by the floating body related to the weight of the body itself?

Answer

Below diagram shows the forces acting on a body floating in water with it's some part submerged:

The forces acting on the body are —

(i) The weight W of body acting vertically downwards, through the centre of gravity G of the body. This force has a tendency to sink the body.

(ii) The upthrust F_B of the liquid acting vertically upwards, through the centre of buoyancy B i.e., the centre of gravity of the displaced liquid. This force has a tendency to make the body float.

The weight of the water displaced by the floating body is equal to the weight of the floating body.

Question 3

A body of volume V and density ρ_s, floats with volume v inside a liquid of density ρ_L. Show that $\dfrac{v}{V}$ = $\dfrac{ρ_s}{ρ_L}$.

Answer

Given,

Volume of body = V

Volume of body submerged in liquid = v

Density of body = ρ_s

Density of liquid = ρ_L

Let weight of the body be W. W = volume of the body x density of the body x g = V ρ_s g

Weight of liquid displaced by the body will be equal to upthrust. Let it be F_B.

F_B = volume of the liquid displaced x density of the liquid x g = v ρ_L g

From principle of floatation,

W = F_B

⇒ V ρ_s g = v ρ_L g

⇒ $\dfrac{v}{V}$ = $\dfrac{ρ_s}{ρ_L}$

Hence proved.

Question 4(a)

Explain the following:

Icebergs floating in sea are dangerous for ships.

Answer

Icebergs being lighter than water, float on water with their major part (nearly 90%) inside water and only a small portion (say 10%) outside water. Since, the portion of iceberg inside water surface depends on the density of sea water, therefore, for the driver of ship, it becomes difficult to estimate the size of iceberg. Thus, an iceberg is very dangerous for a ship as it may collide with the ship and cause damage.

Question 4(b)

Explain the following:

An egg sinks in fresh water, but floats in a strong salt solution.

Answer

A strong salt solution is denser than fresh water (i.e. density of strong salt solution is more than that of fresh water), hence it will exert more upthrust on the egg that balances the weight of the egg. Therefore, the egg floats in strong salt solution and sinks in fresh water.

Question 4(c)

Explain the following:

A toy balloon filled with hydrogen rises to the ceiling, but if filled with carbon dioxide sinks to the floor.

Answer

When a light gas like hydrogen (density much less than that of air) is filled in a balloon, the weight of air displaced by the inflated balloon (i.e., upthrust) becomes more than weight of the gas filled and it rises up.

However, reverse happens when the balloon is filled with a heavier gas like carbon dioxide (i.e., the weight of air displaced by the inflated balloon (i.e., upthrust) becomes less than weight of the gas filled and hence, the balloon sinks to the bottom.)

Question 4(d)

Explain the following:

As a ship in harbor is being unloaded, it slowly rises higher in water.

Answer

As a ship in harbour is being unloaded, it slowly rises higher in water because the weight of the ship decreases and it displaces less water and therefore, the ship rises in water till the weight of water displaced balances the weight of unloaded ship.

Question 4(e)

Explain the following:

A balloon filled with hydrogen rises to a certain height and then stops rising further.

Answer

A balloon filled with hydrogen rises to a certain height and then stops rising further, because the density of air decreases with altitude. Therefore, as the balloon gradually goes up, the weight of the displaced air (i.e., upthrust) decreases. It keeps on rising as long as the upthrust on it exceeds it's weight. When upthrust becomes equal to its weight, it stops rising further.

Question 4(f)

Explain the following:

A ship submerges more as it sails from sea water to river water.

Answer

The ship begins to submerge more as it sails from sea water to river water. The water of river is of low density than that of a sea. Therefore, when a loaded cargo ship sails from sea water to river water, it sinks further. The reason is that according to the law of floatation, to balance the weight of ship, a greater volume of water is required to be displaced in water of lower density i.e., river.

Exercise 5(C) — Numericals

Question 1

A rubber ball floats on water with it's 1/3^rd volume outside water. What is the density of rubber ?

Answer

Let,

V = total volume of rubber ball

ρ = density of the rubber ball

Given,

$\dfrac{1}{3}$rd of V is outside water

Therefore, volume inside water

= V - $\dfrac{1}{3}$V

= $\dfrac{2}{3}$V

By the principle of flotation,

Weight of ball = Weight of water displaced by the immersed part of the ball.

and density of water = 1000 kg m^-3

i.e., V x ρ x g = $\dfrac{2}{3}$ V x 1000 x g

Hence,

ρ = $\dfrac{2000}{3}$ = 667 kg m^-3

Hence,

Density of rubber = 667 kg m^-3

Question 2

A block of wood of mass 24 kg floats on water. The volume of wood is 0.032 m³.

Find —

(a) the volume of block below the surface of water,

(b) the density of wood.

(Density of water = 1000 kg m^-3)

Answer

(a) Given,

Mass = 24 kg

Volume = 0.032 m³

Upthrust = Volume of block below the water x density of liquid x acceleration due to gravity

Hence,

$24 \text {kgf} = v \times 1000 \times g \\[0.5em] v = \dfrac{24}{1000} \\[0.5em] \Rightarrow v = 0.024 \text{ m}^{3} \\[0.5em]$

Hence, volume of block below the surface of water = 0.024 m³

(b) By the principle of floatation,

$\dfrac{\text {Volume of immersed part }}{\text{Total volume}} = \dfrac{\text {Density of wood}}{\text {Density of water}}$

and

Density of water = 1000 kg m^-3

Substituting the values in the formula we get,

$\dfrac{0.024}{0.032} = \dfrac{\text {Density of wood}}{1000} \\[0.5em] \Rightarrow \text{Density of wood} = \dfrac{0.024}{0.032} \times 1000 \\[0.5em] = 7.5 \times 10^{2} \text{ kg m}^{-3} \\[0.5em]$

Question 3

A wooden cube of side 10 cm has mass 700 g. What part of it remains above the water surface while floating vertically on the water surface?

Answer

Given,

Side of wooden cube = 10 cm

Hence,

Volume of wooden cube = 10 cm x 10 cm x 10 cm = 1000 cm³

Mass = 700 g

$\text{Density} = \dfrac{\text{mass}}{\text {volume}} \\[0.5em] \therefore \text{Density of wooden cube} = \dfrac{700}{1000} \\[0.5em] = 0.7 \text{ g cm}^{-3}$

By the principle of floatation,

$\dfrac{\text {Volume of immersed part}}{\text{Total volume}} = \dfrac{\text {Density of wood}}{\text {Density of water}}$

Density of water = 1 g cm^-3

Density of wooden cube = 0.7 g cm^-3

$\therefore \dfrac{\text {Volume of immersed part}}{\text{Total volume}} = \dfrac{0.7}{1}$

Hence, fraction submerged = 0.7

Height of wooden cube = 10 cm

Part of woden cube which is submerged = 10 x 0.7 = 7 cm

Therefore, part above water = 10 - 7 = 3 cm

Hence, 3 cm of height of wooden cube remains above water while floating.

Question 4

A piece of wax floats on brine. What fractions of it's volume is immersed?

Density of wax = 0.95 g cm^-3,

Density of brine = 1.1 g cm^-3

Answer

Given,

Density of wax = 0.95 g cm^-3

Density of brine = 1.1 g cm^-3

By the principle of floatation,

$\dfrac{\text {Volume of immersed part}}{\text{Total volume}} = \dfrac{\text {Density of wax}}{\text {Density of brine}} \\[1em] \therefore \dfrac{\text {Volume of immersed part}}{\text{Total volume}} = \dfrac{0.95}{1.1} \\[0.5em] = 0.86$

Hence, the piece of wax floats with 0.86^th part of it's volume immersed in brine surface.

Question 5

If the density of ice is 0.9 g cm^-3, what portion of an iceberg will remain below the surface of water in a sea? (Density of sea water = 1.1 g cm^-3)

Answer

Given,

Density of ice = 0.9 g cm^-3

Density of sea water = 1.1 g cm^-3

By the principle of floatation,

$\dfrac{\text {Volume of immersed part}}{\text{Total volume}} = \dfrac{\text {Density of ice}}{\text {Density of sea water}} \\[1em] \therefore \dfrac{\text {Volume of immersed part}}{\text{Total volume}} = \dfrac{0.9}{1.1} \\[0.5em] = \dfrac{9}{11} = 0.818$

Hence, the volume of iceberg that will remain below the surface of water in the sea = $\dfrac{9}{11}$th of total volume (or 0.818th) part.

Question 6

A piece of wood of uniform cross section and height 15 cm floats vertically with it's height 10 cm in water and 12 cm in spirit. Find the density of (i) wood and (ii) spirit.

Answer

Given,

Height of the wood = 15 cm

Height of the wood in water = 10 cm

Height of the wood in spirit = 12 cm

As the block of wood is of uniform cross-sectional area, the height of the block is proportional to the volume

By the principle of floatation,

$\dfrac{\text {Volume of immersed part}}{\text{Total volume}} = \dfrac{\text {Density of wood}}{\text {Density of water}} \\[1em] \therefore \dfrac{10}{15} = \dfrac{\text {Density of wood}}{1} \\[0.5em] \Rightarrow \text{Density of wood} = \dfrac{10}{15} = 0.667 \text {g cm}^{-3}$

In the case of spirit, substituting the values in the formula above, we get,

$\dfrac{\text {Volume of immersed part}}{\text{Total volume}} = \dfrac{\text {Density of wood}}{\text {Density of spirit}} \\[0.5em] \dfrac{12}{15} = \dfrac{0.667}{\text{Density of spirit}} \\[0.5em] \text{Density of spirit} = \dfrac{15}{12} \times 0.667 = 0.833 \text { g cm}^{-3} \\[0.5em]$

Question 7

A wooden block floats in water with two-third of it's volume submerged. (a) Calculate the density of wood. (b) When the same block is placed in oil, three-quarter of it's volume is immersed in oil. Calculate the density of oil.

Answer

(a) Let volume of wooden block be V.
Volume of block submerged in water = $\dfrac{2}{3}V$

Density of water = 1000 kg m^-3

By the principle of floatation,

$\dfrac{\text {Volume of immersed part}}{\text{Total volume}} = \dfrac{\text {Density of wood}}{\text {Density of water}} \\[1em] \therefore \dfrac{\dfrac{2}{3}V}{V} = \dfrac{\text {Density of wood}}{1000} \\[0.5em] \Rightarrow \text{Density of wood} = \dfrac{2}{3} \times 1000 = 666.6666 \text { kg m}^{-3} \approx 667 \text { kg m}^{-3}$

(b) Volume of block submerged in oil = $\dfrac{3}{4}V$

By the principle of floatation,

$\dfrac{\text {Volume of immersed part}}{\text{Total volume}} = \dfrac{\text {Density of wood}}{\text {Density of oil}} \\[1em] \therefore \dfrac{\dfrac{3}{4}V}{V} = \dfrac{\text {667}}{\text{Density of oil}} \\[0.5em] \Rightarrow \text{Density of oil} = \dfrac{4}{3} \times 667 = 889.33 \text { kg m}^{-3} \approx 889 \text { kg m}^{-3}$

Question 8

The density of ice is 0.92 g cm^-3 and that of sea water is 1.025 g cm^-3. Find the total volume of an iceberg which floats with it's volume 800 cm³ above water.

Answer

Given,

Density of ice = 0.92 g cm^-3

Density of sea water = 1.025 g cm^-3

Let total volume of iceberg be V cm³

Volume of iceberg above sea water = 800 cm³

Volume of iceberg immersed in sea water = (V - 800) cm³

By the principle of floatation,

$\dfrac{\text {Volume of immersed part}}{\text{Total volume}} = \dfrac{\text {Density of ice}}{\text {Density of water}} \\[1em] \therefore \dfrac{(V - 800)}{V} = \dfrac{0.92}{1.025} \\[0.5em] \Rightarrow 1.025V - 820 = 0.92V \\[0.5em] \Rightarrow 1.025V - 0.92V = 820 \\[0.5em] \Rightarrow 0.105V = 820 \\[0.5em] \Rightarrow V = \dfrac{820}{0.105} = 7809.52 \text{ cm}^3$

Hence,

Total volume of iceberg = 7809.52 cm³

Question 9

A weather forecasting plastic balloon of volume 15 m³ contains hydrogen of density 0.09 kg m^-3. The volume of an equipment carried by the balloon is negligible compared to it's own volume. The mass of empty balloon alone is 7.15 kg. The balloon is floating in air of density 1.3 kg m^-3. Calculate : (i) the mass of hydrogen in the balloon, (ii) the mass of hydrogen and balloon, (iii) the total mass of hydrogen, balloon and equipment if the mass of equipment is x kg, (iv) the mass of air displaced by balloon and (v) the mass of equipment using the law of floatation.

Answer

Given,

Volume of the plastic balloon = 15 m³

Density of hydrogen = 0.09 kg m^-3

Mass of the unfilled balloon = 7.15 kg

Density of air = 1.3 kg m^-3

(i) As we know,

Mass = volume of balloon x density of hydrogen

Substituting the value in the formula we get,

15 x 0.09 = 1.35 kg

Hence, mass of hydrogen in the balloon = 1.35 kg

(ii) Mass of hydrogen and balloon = mass of hydrogen in the balloon + mass of unfilled balloon = 7.15 + 1.35 = 8.5 kg

Hence, mass of hydrogen and balloon = 8.5 kg

(iii) Given,

mass of equipment = x kg

Hence,

Total mass of hydrogen, balloon and equipment = (8.5 + x) kg

(iv) Weight of the air displaced = upthrust = Volume of the balloon x density of the balloon x g

Hence,

Mass of the air displaced = volume of balloon x density of air = 15 x 1.3 = 19.5 kg

(v) By law of floatation,

Mass of the air displaced = total mass of hydrogen, balloon and equipment

Substituting the values in the formula we get,

$19.5 = 8.5 + x \\[0.5em] x = 19.5 - 8.5 \\[0.5em] x = 11 \text { kg} \\[0.5em]$

Hence, mass of the equipment = 11 kg