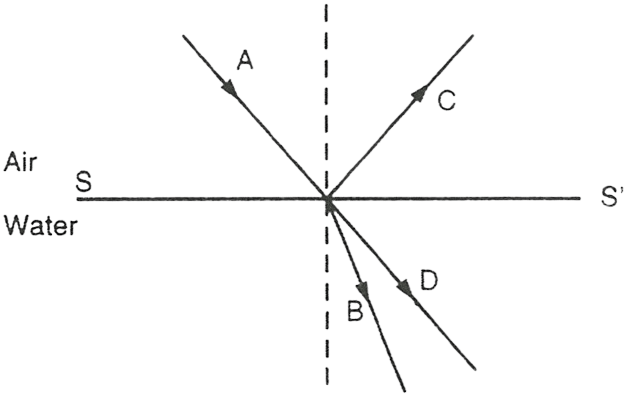
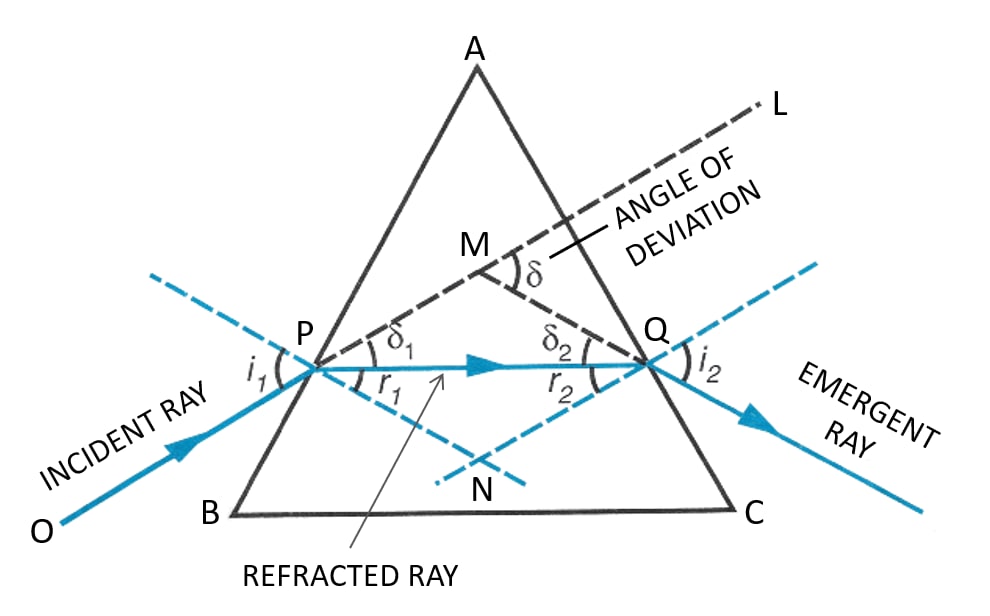
In the diagram shown below which one of the following statements is true?
- C is incident ray and A is reflected ray
- A is incident ray and D is refracted ray
- A incident ray and B is refracted ray
- B is incident ray and C is refracted ray
Answer
A incident ray and B is refracted ray.
Reason — As A is the incoming ray so it is the incident ray and C is the reflected ray. Ray B bends towards the normal and it is the refracted ray.
When a ray of light from air enters a denser medium, it:
- bends away from the normal
- bends towards the normal
- goes undeviated
- is reflected back
Answer
bends towards the normal
Reason — When a ray of light from air enters a denser medium, it bends towards the normal due to the change in speed. This phenomenon is known as refraction. This bending towards the normal occurs because the speed of light is slower in the denser medium. The change in speed causes the light wavefront to change direction, resulting in the bending of the light ray towards the normal.
A light ray does not bend at the boundary in passing from one medium to the other medium if the angle of incidence is:
- 0°
- 45°
- 60°
- 90°
Answer
0°
Reason — A ray of light incident normally on the surface separating the two media, passes undeviated (i.e., such a ray suffers no bending at the surface). Here, angle of incidence and angle of refraction = 0°
The diagram given below shows light travelling from air into glass. Four angles A, B, C and D are shown. Which of the following formulae is used to calculate the refractive index μ of the glass?

μ =
μ =
μ =
μ =
Answer
μ =
Reason — The refractive index of second medium with respect to the first medium is defined as the ratio of the sine of the angle of incidence in the first medium to the sine of the angle of refraction in the second medium.
∴ Refractive index of glass with respect to air (μ) =
where
B = angle of incidence in air
r = angle of refraction in glass
The incorrect statement among the following is:
- When a ray of light gets refracted from a denser to a rarer medium, the speed of light decreases.
- The frequency of light does not change on refraction.
- The speed of light V in a medium is related to its wavelength λ and frequency f as V = fλ
- The incident ray, the refracted ray and the normal at the point of incidence all lie in one plane.
Answer
When a ray of light gets refracted from a denser to a rarer medium, the speed of light decreases.
Reason — When a ray of light gets refracted from a denser to a rarer medium, the speed of light increases due to the change in the refractive index of the medium.
In refraction of light, the relation between incident angle i and refracted angle r is:
- i > r
- r > i
- i = r
- there is no fixed relation.
Answer
there is no fixed relation
Reason — There is no fixed relation between the incident angle i and refracted angle r because:
- when a ray of light travels from a rarer medium to a denser medium, it bends towards the normal hence ∠r < ∠i
- when a ray of light travels from a denser medium to a rarer medium, it bends away from the normal hence ∠r > ∠i
- when a ray of light is incident normally on the surface separating the two media, it passes undeviated hence ∠r = ∠i.
The intensity of the refracted light is always ............... the intensity of incident light:
- greater than
- equal to
- less than
- none of the above
Answer
less than
Reason — The intensity of the refracted light is always less than the intensity of incident light because a part of the incident light has suffered reflection.
The ray AO is shown in the figure given below. The path of refracted ray and emergent ray will be:
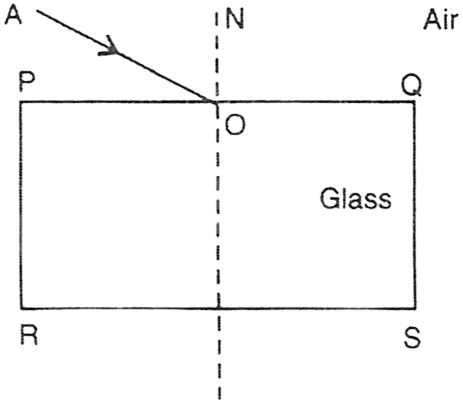
(1) the refracted ray will bend towards normal
(2) the refracted ray will bend away from normal
(3) the emergent ray will bend towards normal
(4) emergent ray will bend away from normal
- (1) and (3)
- (1) and (4)
- (2) and (3)
- (2) and (4)
Answer
(1) and (4)
Reason — As air is a rarer medium and glass is a denser medium hence, the light ray passes from a rarer to a denser medium hence, the refracted ray will bend in towards normal whereas emergent ray will bend away from normal.
What is the deviation of a ray of light which is incident normally on the surface of two separating media :
- 0°
- 45°
- 90°
- 180°
Answer
0°
Reason — A ray of light incident normally on the surface separating the two media, passes undeviated (i.e., such a ray suffers no bending at the surface). Here, angle of incidence and angle of refraction = 0°
If refractive indices of medium 1 and medium 2 are same, the speed of light will:
- increase
- decrease
- remain the same
- none
Answer
remain the same
Reason — If the refractive indices of two media are the same, it means that light travels at the same speed in both media.
When light passes from a denser medium to a rarer medium, its wavelength :
- decreases
- increases
- remains the same
- none
Answer
increases
Reason — The speed of light differs in different mediums due to their varying optical densities. In denser mediums, light travels slower, while in rarer mediums, it travels faster. According to the equation c = λ × f, where c is the speed of light, λ is the wavelength, and f is the frequency, if the speed of light decreases (as it does when entering a denser medium), and f remains constant, then λ must increase to compensate. Conversely, when light from a denser medium enters a rarer medium, its speed increases, and hence, its wavelength increases as well.
Which of the following is correct when a ray of light passes from a rarer medium to a denser medium:
(1) speed will decrease
(2) frequency remains unchanged
(3) wavelength will decrease
(4) intensity will decrease
- (1)
- (1) and (4)
- (1), (2) and (4)
- all of the above
Answer
all of the above
Reason — When a ray of light passes from a rarer medium to a denser medium, the speed decreases due to the change in the refractive index of the medium. Frequency remains constant due to the nature of light itself, whereas, wavelength decreases as a consequence of the change in speed. Intensity also decreases as part of the light ray suffers reflection.
The refractive index of water is 4/3 and that of glass is 3/2. The refractive index of glass with respect to water is:
- 9/8
- 2
- 8/9
- 1
Answer
9/8
Reason — Given,
aμw =
aμg =
wμg =
Substituting we get,
wμg = = =
The optical density of turpentine is higher than that of water, while its mass density is lower than water. The figure given below shows a layer of turpentine floating over water taken in a container. For which one of the four rays incident on turpentine in the path shown in the figure is correct?
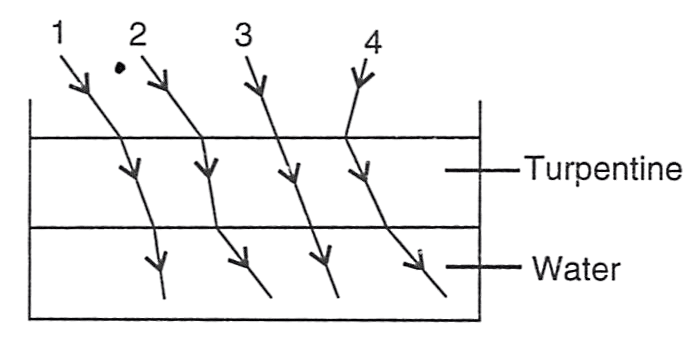
- Ray 1
- Ray 2
- Ray 3
- Ray 4
Answer
Ray 2
Reason — Here water is rarer medium and turpentine is denser medium and when light travels from denser to rarer medium it bends away from the normal and vice versa.
Ray 1 : As it enters from turpentine to water then it should bend away from the normal but here it is bending towards the normal.
Ray 2 : It follows laws of refraction perfectly since it is bending towards normal while entering turpentine and away from it while entering water.
Ray 3 : It shows no deflection while entering any medium which doesn't happen in refraction.
Ray 4 : It is bending away from the normal while entering turpentine whereas it should bend towards the normal.
With respect to light passing from air into water, which of the following statements is correct?
- Angle of incidence is equal to the angle of refraction.
- Angle of incidence is always greater than the angle of refraction
- Angle of incidence is always less than the angle of refraction
- Angle of incidence has no effect on the angle of refraction.
Answer
Angle of incidence is always greater than the angle of refraction
Reason — As light enters the denser medium, it bends towards the normal, resulting in a smaller angle of refraction compared to the angle of incidence.
A ray of light is incident normally on a plane glass slab. What will be (i) the angle of refraction and (ii) the angle of deviation for the ray?
Answer
(i) The ray of light incident normally on a plane glass slab passes undeviated, ( i.e. such a ray suffers no bending at the surface). Thus, if angle of incidence ∠i = 0°, then the angle of refraction ∠r = 0°.
(ii) In the case when ray of light is incident normally on a plane glass slab, it passes undeviated. Hence, the angle of deviation is 0°.
An obliquely incident light ray bends at the surface due to change in speed, when passing from one medium to other. The ray does not bend when it is incident normally. Will the ray have different speed in the other medium?
Answer
We observe that, when a ray of light passing from one medium to other is obliquely incident it bends at the surface due to change in speed in going from one medium to another.
However, for normal incidence from one medium to another, angle of incidence ∠i = 0° then the angle of refraction ∠r = 0°. Hence the speed of light changes but the direction of light does not change.
A ray of light passes from medium 1 to medium 2. Which of the following quantities of the refracted ray will differ from that of the incident ray: speed, intensity, frequency and wavelength?
Answer
Speed, intensity and wavelength are the quantities which will differ for a refracted ray in comparison to those of a incident ray.
The frequency of light depends on the source of light, so it does not change on refraction.
When a ray of light gets refracted from a rarer to a denser medium, the speed of light decreases; while if it is refracted from a denser to a rarer medium, the speed of light increases.
When light passes from a rarer to a denser medium, the wavelength decreases and when it passes from denser to rarer medium, its wavelength increases.
A light ray passes from water to (i) air, and (ii) glass. In each case, state how does the speed of light change?
Answer
As we know,
Refractive index of air, μa = 1.0003
Refractive index of water, μw = 1.33
Refractive index of ordinary glass, μg = 1.5
With the help of the above values, we can see that μg > μw > μa
When a ray of light gets refracted from a rarer to a denser medium, the speed of light decreases, while if it is refracted from a denser to a rarer medium, the speed of light increases.
So on the basis of above information, we can say that —
(i) When a ray of light passes from water to air, its speed increases as it is moving from a denser to a rarer medium.
(ii) When a ray of light passes from water to glass, its speed decreases as it is moving from a rarer to a denser medium.
(a) For which colour of white light, is the refractive index of a transparent medium
(i) the least
(ii) the most?
(b) Which colour of white light travels fastest in any medium except air?
Answer
(a) (i) The speed of red light is maximum. Therefore, the refractive index of a transparent medium is least for red colour.
(ii) The speed of violet light is least. Therefore, the refractive index of a transparent medium is most for violet colour.
(b) The wavelength of visible light increases from violet to red colour. It is highest for red colour. Hence, red colour travels fastest in any medium except air.
How does the refractive index of a medium depend on the wavelength of light used?
Answer
In a given medium, the speed of red light is maximum. Therefore, the refractive index of that medium is maximum for violet light and least for red light. (i.e. μviolet > μred).
The wavelength of visible light increases from violet to red end, so the refractive index of a medium decreases with increase in wavelength of light used.
Hence, the refractive index of a medium for violet light which has the least wavelength is greater than that for red light which has the greatest wavelength.
How does the refractive index of a medium depend on its temperature?
Answer
With increase in temperature, the speed of light in a medium increases, so the refractive index of the medium decreases.
The refractive index of water with respect to air is aμw and of glass with respect to air is aμg. Express the refractive index of glass with respect to water.
Answer
The refractive index of water with respect to air is aμw.
The refractive index of glass with respect to air is aμg.
So, the refractive index of glass with respect to water is given by
Fill in the blanks to complete the following sentences —
(a) When light travels from a rarer to a denser medium, its speed ...............
(b) When light travels from a denser to a rarer medium, its speed ...............
Answer
(a) When light travels from a rarer to a denser medium, its speed decreases
(b) When light travels from a denser to a rarer medium, its speed increases.
What do you understand by refraction of light?
Answer
The change in the direction of the path of light, when it passes from one transparent medium to another transparent medium, is called refraction of light. The refraction of light is essentially a surface phenomenon.
What is the cause of refraction of light when it passes from one medium to another?
Answer
When a ray of light passes from one medium to another medium, its direction (or path) changes because of the change in speed of light in going from one medium to another.
In passing from one medium to other, if light slows down, it bends towards the normal and if light speeds up, it bends away from the normal.
If the speed of light remains same in passing from one medium to another, the ray of light does not bend then it passes undeviated.
Hence, we can say that the cause of refraction of light is that its speed is different in different mediums.
State the Snell's laws of refraction of light.
Answer
The Snell’s laws of refraction of light are:
(i) The incident ray, the refracted ray and the normal at the point of incidence, all lie in the same plane.
(ii) The ratio of the sine of the angle of incidence i to the sine of the angle of refraction r is constant for the pair of given media.
The constant 1μ2 is called the refractive index of the second medium with respect to the first medium.
Define the term refractive index of a medium. Can it be less than 1?
Answer
The refractive index of the second medium with respect to the first medium is defined as the ratio of the sine of the angle of incidence in the first medium to the sine of the angle of refraction in the second medium.
The refractive index of a transparent medium is always greater than 1 (it cannot be less than 1) because the speed of light in any medium is always less than that in vacuum ( i.e. V < c ) and μ = 1 for air or vacuum.
(a) Compare the speeds of light of wavelength 4000Å (i.e. violet light) and 8000Å (i.e. red light) in vacuum.
(b) How is the refractive index of a medium related to the speed of light in it and in vacuum or air?
Answer
(a) As we know that light is an electromagnetic wave and it travels with same speed for all wavelength, which is equal to 3 x 108.
Hence, the ratio of speeds of light of wavelength 4000Å (i.e. violet light) and 8000Å (i.e. red light) in vacuum = 1:1.
(b) The refractive index of a medium is defined as the ratio of the speed of light in vacuum (or air) to the speed of light in that medium.
Denser medium has a higher refractive index. Hence, the speed of light in such medium is lower in comparison to the speed of light in a medium which has a lower refractive index.
A light ray in passing from water to a medium (a) speeds up (b) slows down. In each case, (i) give one example of the medium, (ii) state whether the refractive index of medium is equal to, less than or greater than the refractive index of water.
Answer
As we know that, when a ray of light gets refracted from a rarer to a denser medium, the speed of light decreases, while if it is refracted from a denser to a rarer medium, the speed of light increases.
(a) (i) When a ray of light passes from water to air, its speed increases as it is moving from a denser to a rarer medium.
(b) (i) When a ray of light passes from water to glass, its speed decreases as it is moving from a rarer to a denser medium.
(a) (ii) The refractive index of the medium (air) is less than that of water as the speed of refracted ray increases.
(b) (ii) The refractive index of the medium (glass) is more than that of water as the speed of refracted ray decreases.
What do you understand by the statement 'the refractive index of glass is 1.5 for white light'?
Answer
This statement indicates that white light travels in air 1.5 times faster than in glass or speed of light in glass is times the speed of light in air.
A monochromatic ray of light passes from air to glass. The wavelength of light in air is λ, the speed of light in air is c and in glass is V. If the refractive index of glass is 1.5, write down,
(a) the relationship between c and V,
(b) the wavelength of light in the glass.
Answer
(a) The relation between the speed of light in air c and in glass V is given by —
(b) Let wavelength of light in glass be λ1 so we get,
A boy uses blue colour of light to find the refractive index of glass. He then repeats the experiment using red colour of light. Will the refractive index be the same or different in the two cases? Give a reason to support your answer.
Answer
The speed of blue light in glass is less that of red light.
i.e. cb < cr
We know that,
Hence, the refractive index of blue light is greater than that of red light.
i.e. μb > μr.
Hence, the refractive index of red and blue light in glass will be different.
Name two factors on which the refractive index of a medium depends? State how does it depends on the factors stated by you.
Answer
The factors on which the refractive index of a medium depends are as follows —
(i) Nature of the medium (on the basis of speed of light) — Less the speed of light in the medium as compared to that in air, more is the refractive index of the medium.
We know that,
Vglass = 2 x 10 8 ms-1, μglass = 1.5
Vwater = 2.25 x 10 8 ms-1, μwater = 1.33
(ii) Physical condition such as temperature — With an increase in temperature, the speed of light in medium increases, so the refractive index of the medium decreases.
Light of a single colour is passed through a liquid having a piece of glass suspended in it. On changing the temperature of the liquid, at a particular temperature, the glass piece is not seen.
(i) When is the glass piece not seen?
(ii) Why is the light of a single colour used?
Answer
(i) The glass piece is not seen when the refractive index of the liquid becomes equal to the refractive index of glass.
(ii) The light of a single colour is used as the refractive index of a medium (glass or liquid) is different for the light of different colours.
When an illuminated object is held in front of a thick plane glass mirror, several images are seen, out of which the second image is the brightest. Give reason.
Answer
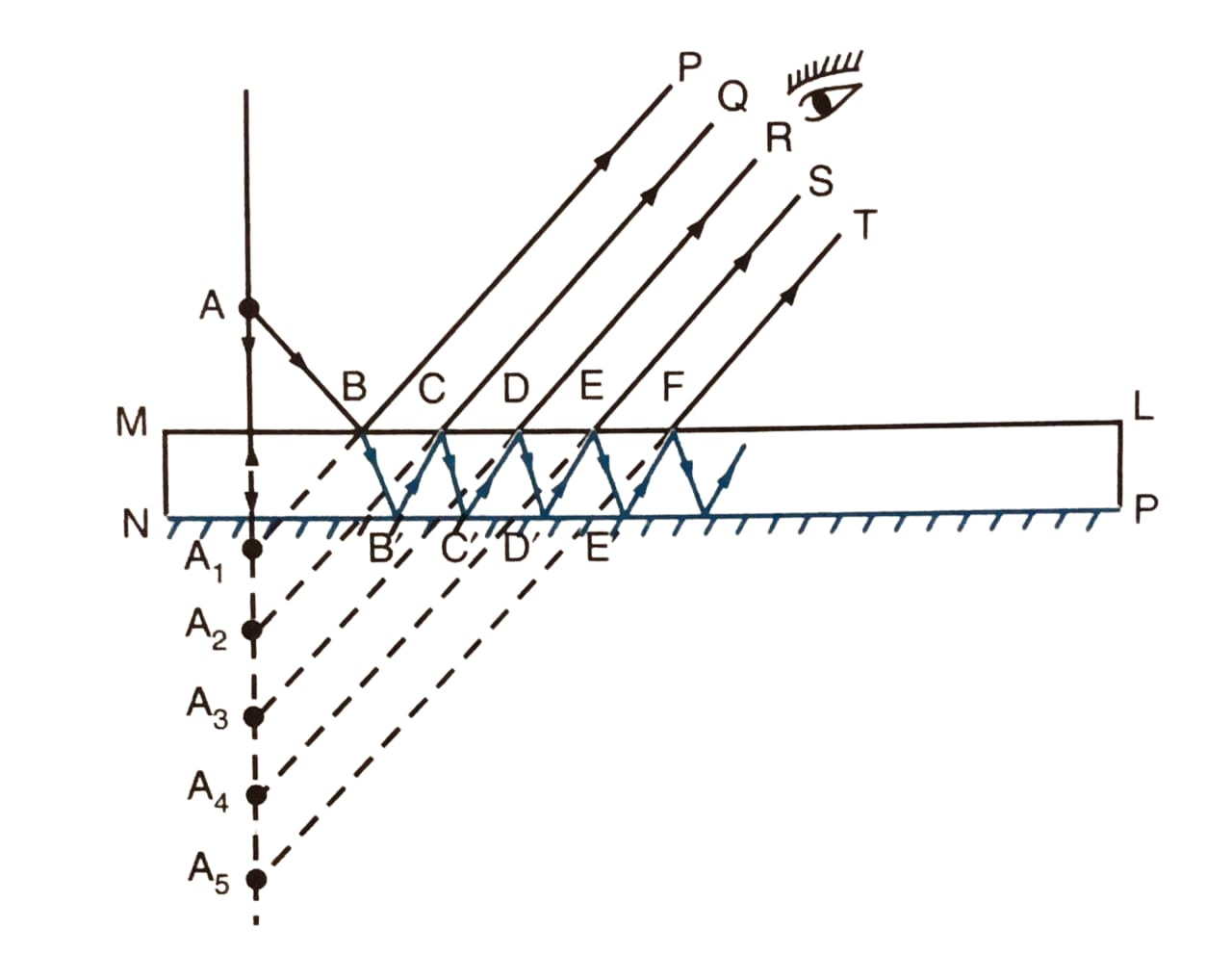
As shown in the figure, if an illuminated object is held in front of a thick plane glass mirror, and is viewed obliquely, a number of images are seen and out of these the second image is the brightest.
The reason for this is that when a ray of the light falls on the surface of the mirror from the source, a small part of light (nearly 4%) is reflected forming a faint virtual image, while a large part of light (nearly 96%) is refracted inside the glass.
Now, we can see that this ray is strongly reflected back by the silvered surface inside the glass. This ray is then partially refracted in air and this refracted ray forms another virtual image.
This image is the brightest image because it is due to the light suffering a strong first reflection at the silvered surface.
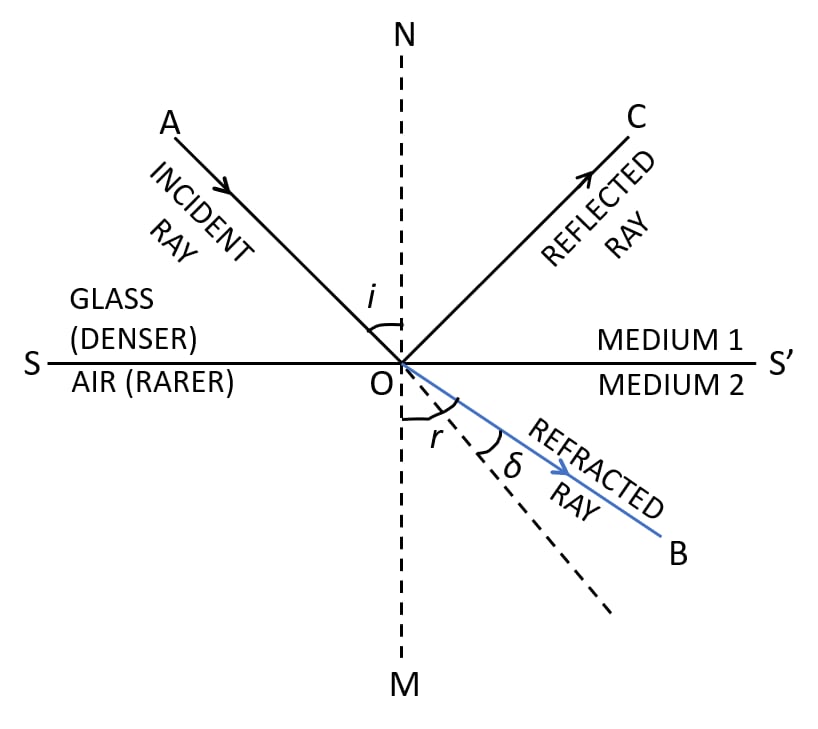
Draw diagrams to show the refraction of light from (i) air to glass, (ii) glass to air. In each diagram, label the incident ray, refracted ray, the angle of incidence (i) and the angle of refraction (r).
Answer
(i) The below ray diagram shows the refraction of light from air to glass:
(ii) The below ray diagram shows the refraction of light from glass to air:
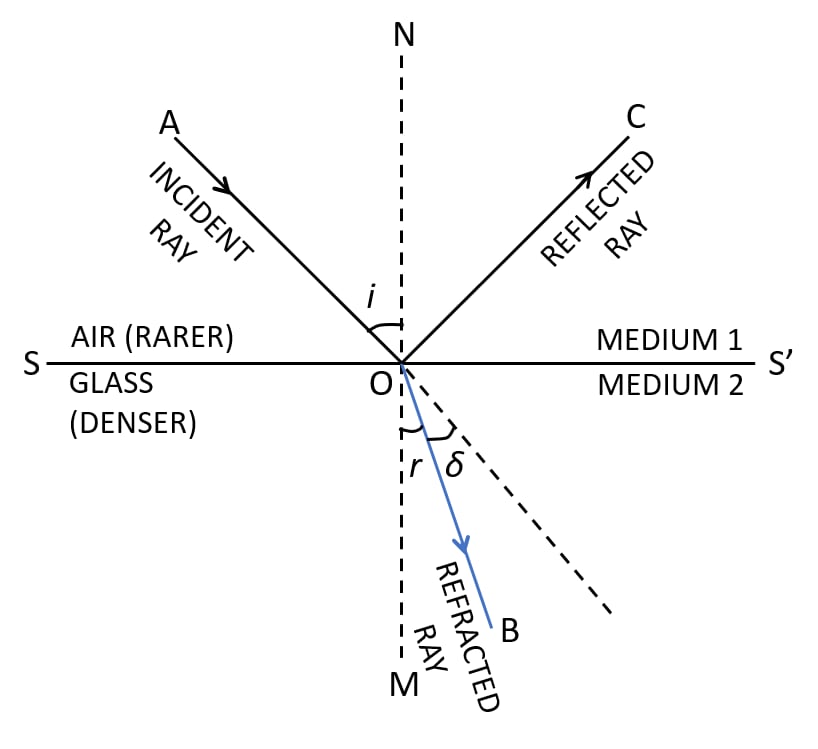
A light ray suffers reflection and refraction at the boundary in passing from air to water. Draw a neat labelled diagram to show it.
Answer
Air is a rarer medium while water is denser medium than air. Therefore, when a ray of light travels from air to water (i.e rarer to denser) it bends towards the normal. Below diagram shows reflection and refraction suffered by a light ray at the boundary in passing from air to water:
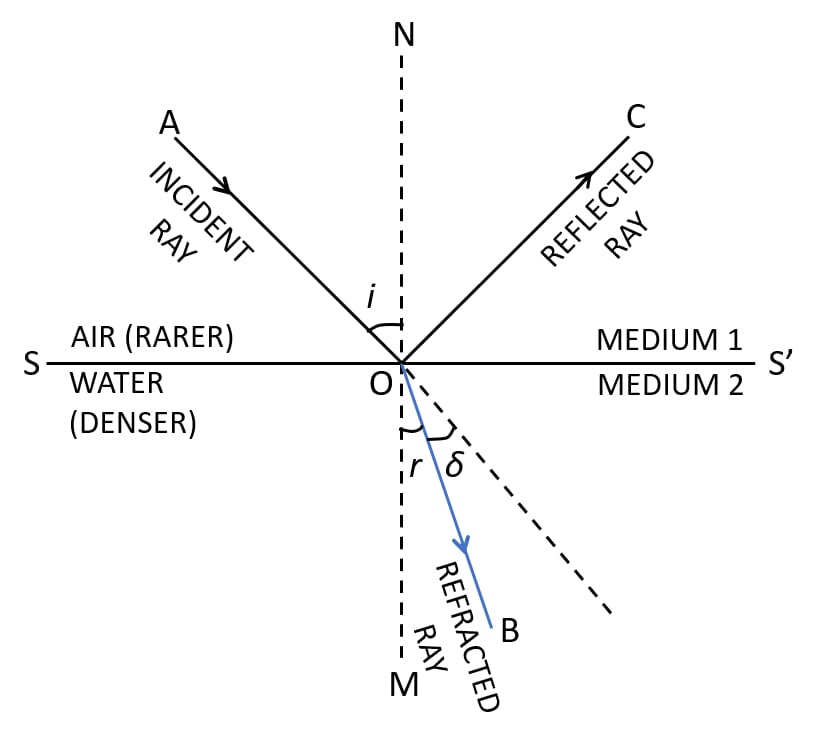
In the figure below, a ray of light A incident from air suffers partial reflection and refraction at the boundary of water.
(a) Complete the diagram showing (i) the reflected ray B and (ii) the refracted ray C.
(b) How are the angles of incidence i and refraction r related?
Answer
(a) Below is the completed diagram with the refracted ray B and the reflected ray C labelled:

(b) The relation between angle of incidence i and the angle of refraction r is given by Snell’s law as,
The ratio of the sine of the angle of incidence i to the sine of the angle of refraction r is constant for the pair of given media.
The constant 1μ2 is called the refractive index of the second medium with respect to the first medium
The diagram alongside shows the refraction of a ray of light from air to a liquid.
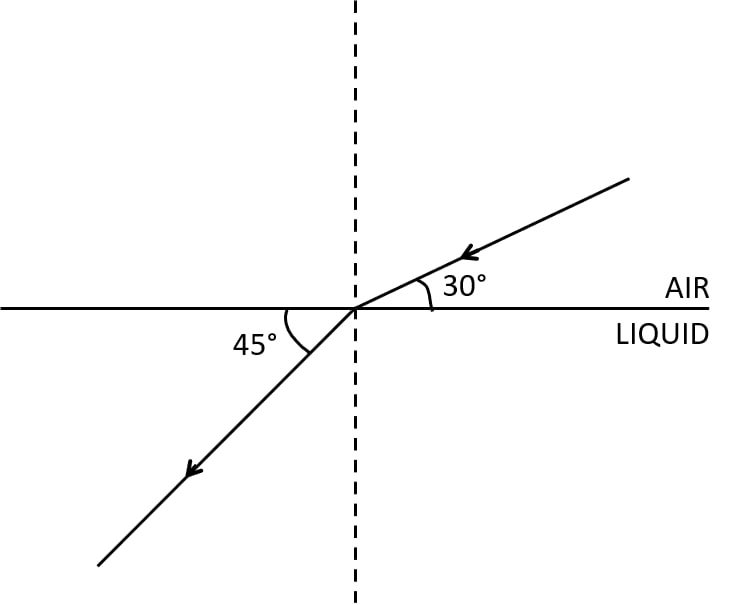
(a) Write the values of (i) angle of incidence, and (ii) angle of refraction.
(b) Use Snell's law to find the refractive index of liquid with respect to air.
Answer
(a) (i) The angle of incidence is the angle which the incident ray makes with the normal. Hence, ∠i = 90° – 30° = 60°.
(ii) Angle of refraction is the angle which the refracted ray makes with the normal Hence, ∠r = 90° – 45° = 45°.
(b) We know that according to Snell’s law,
Hence, the refractive index of liquid with respect to air is 1.22
What is lateral displacement? Draw a ray diagram showing the lateral displacement of a ray of light when it passes through a parallel-sided glass slab.
Answer
The perpendicular distance between the incident ray and the emergent ray is defined as lateral displacement. This shift depends upon the angle of incidence, the angle of refraction and the thickness of the medium.
Below diagram shows the lateral displacement of a ray of light when it passes through a parallel-sided glass slab:
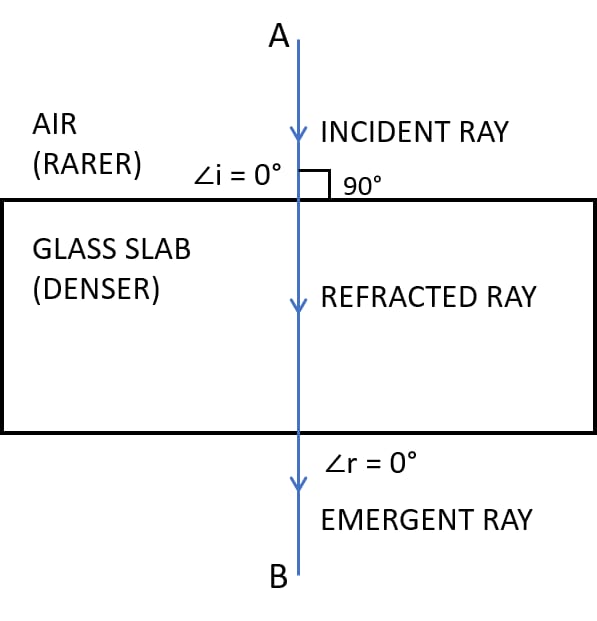
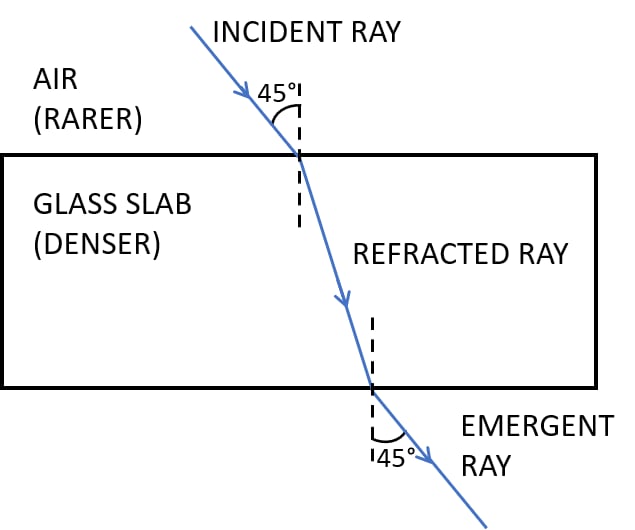
A ray of light strikes the surface at a rectangular glass slab such that the angle of incidence in air is (i) 0°, (ii) 45°. In each case, draw a diagram to show the path taken by the ray as it passes through the glass slab and emerges from it.
Answer
(i) Below is the labelled diagram for ray of light at angle of incidence 0°:
(ii) Below is the labelled diagram for ray of light at angle of incidence 45°:
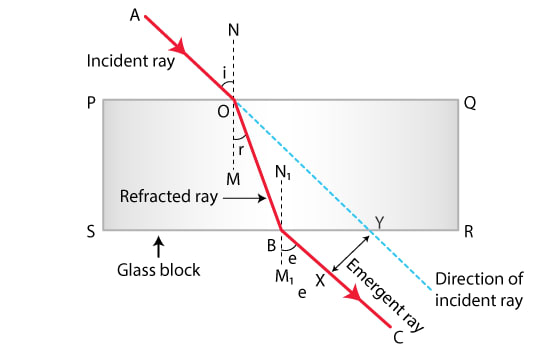
In the adjacent diagram, AO is a ray of light incident on a rectangular glass slab.
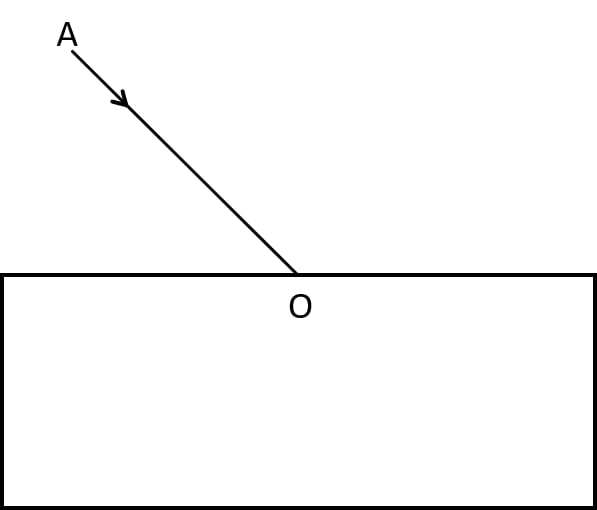
(a) Complete the path of the ray until it emerges out of the slab.
(b) In the diagram, mark the angle of incidence (i) and the angle of refraction (r) at the first interface. How is the refractive index of glass related to angles i and r?
(c) Mark angle of emergence by the letter e. How are the angles i and e related?
(d) Which two rays are parallel to each other? Name them.
(e) Indicate in the diagram the lateral displacement between the emergent ray and the incident ray. State one factor that affects the lateral displacement.
Answer
(a) The below diagram shows the path of the ray until it emerges out of the slab:

(b) In diagram, the angle of incidence (i) and the angle of refraction (r) are marked.
Refractive index of glass μ is related to the angle of incidence (i) and angle of reflection (r) by Snell's second law and is represented as —
The ratio of the sine of the angle of incidence i to the sine of the angle of refraction r is constant for the pair of given media
The constant 1μ2 is called the refractive index of the second medium with respect to the first medium.
(c) The angle of emergence (e) is marked in diagram.
As the refraction occurs at two parallel surfaces PQ and RS, therefore angle MOB = angle N1BO and by the principle of reversibility of the path of a light ray angle of emergence (e) is equal to the angle of incidence (i).
(d) As the refraction occurs at two parallel surfaces PQ and RS, therefore angle MOB = angle N1BO and by the principle of reversibility of the path of a light ray angle of emergence (e) is equal to the angle of incidence (i).
Hence, the emergent ray BC is parallel to the incident ray AO.
(e) The lateral displacement between the incident ray and the emergent ray is represented by XY.
One of the factors that affects lateral displacement is the the thickness of the medium. More the thickness of the medium more is the lateral displacement.
A ray of green light enters a liquid from air, as shown in the figure. The angle 1 is 45° and angle 2 is 30°.
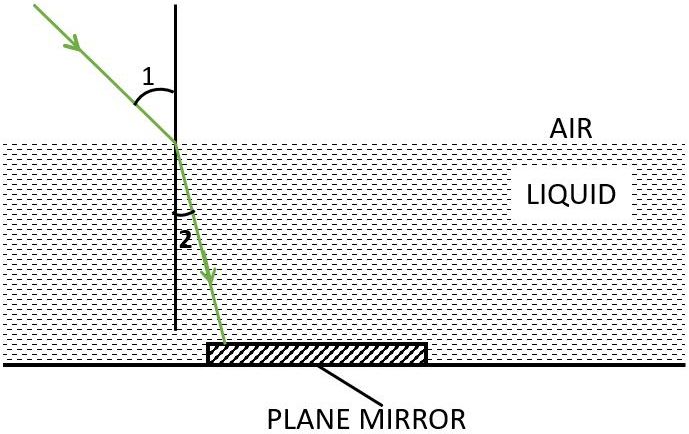
(a) Find the refractive index of liquid.
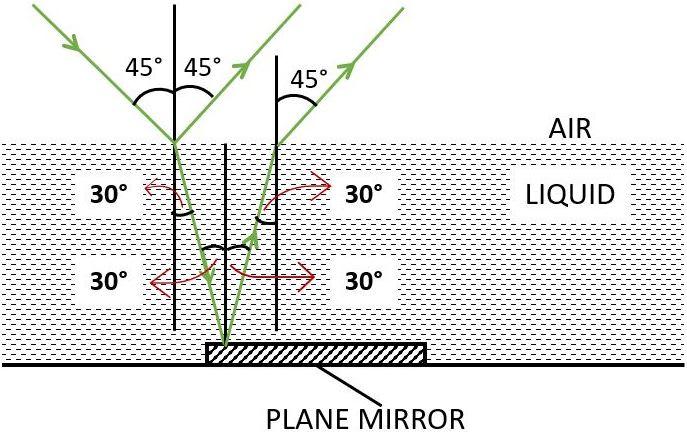
(b) Show in the diagram the path of the ray after it strikes the mirror and re-enters in air. Mark in the diagram the angles wherever necessary.
(c) Redraw the diagram if plane mirror becomes normal to the refracted ray inside the liquid. State the principle used.
Answer
(a) Refractive index of the liquid is given by Snell's law and is shown as below,
airμliquid =
airμliquid =
(b) Below labelled diagram shows the path of the ray after it strikes the mirror and re-enters in air:
(c) Below labelled diagram shows the path of the ray when it strikes the plane mirror normally inside the liquid:
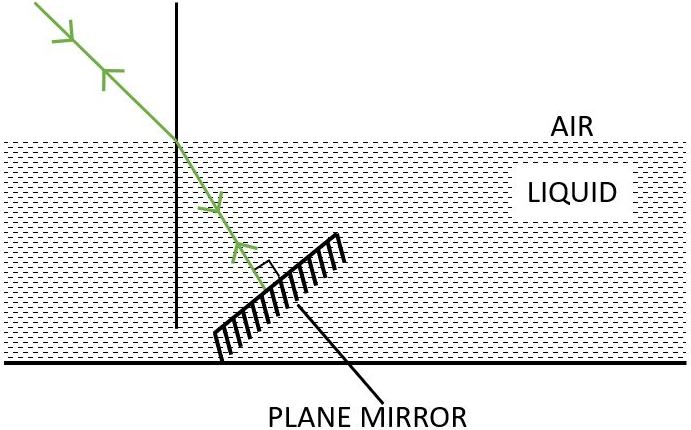
The principle of reversibility is used.
The speed of light in air is 3 x 108 m s-1. Calculate the speed of light in glass. The refractive index of glass is 1.5.
Answer
As we know,
Given,
Refractive index of glass, μ = 1.5
Speed of light in air, C = 3 × 108 m / s
Substituting the values in the formula above we get,
Hence, Speed of light in glass = 2 × 108 m s-1
The speed of light in diamond is 125,000 km s-1. What is the refractive index? (Speed of light in air = 3 x 108 m s-1).
Answer
As we know,
Given,
Speed of light in diamond = 125,000 km s-1 = 125 x 106 m/s
Speed of light in air, c = 3 × 108 ms-1
Substituting the values in the formula above we get,
Hence, refractive index = 2.4
The refractive index of water with respect to air is 4/3. What is the refractive index of air with respect to water?
Answer
As it is given that,
aμw =
And we know that —
wμa =
wμa =
wμa = 0.75
Hence, the refractive index of air with respect to water is 0.75
A ray of light of wavelength 6600 Å suffers refraction from air to glass. Taking aμg = 3/2, find the wavelength of light in glass.
Answer
As we know that,
Given,
Refractive index of glass with respect to air is given by aμg =
Wavelength of light in air = 6600 Å
Substituting the values in the formula above we get,
Hence, wavelength of light in glass = 4400 Å
In refraction of light through a prism, the light ray:
- suffers refraction only at one face of the prism
- emerges out from the prism in a direction parallel to the incident ray
- bends at both the surfaces of the prism towards its base
- bends at both the surfaces of prism opposite to its base.
Answer
bends at both the surfaces of the prism towards its base
Reason — This phenomenon occurs because light undergoes refraction twice as it enters and exits the prism. At each surface, the light bends towards the normal due to the change in medium, causing it to deviate from its original path. Since the prism is thicker at the base and thinner at the apex, the net effect of refraction at both surfaces is to bend the light towards the base of the prism.
A ray of light suffers refraction through an equilateral prism. The deviation produced by the prism does not depend on the:
- angle of incidence
- colour of light
- material of prism
- size of prism
Answer
size of prism
Reason — The deviation produced by the prism depends on :
- the angle of incidence
- the material of prism
- the angle of prism
- the colour or wavelength of light used.
It does not depend on the size of prism.
In the figure given ahead the correct statement is:
- ABED and ABC are the refracting surfaces.
- line AD is the refracting edge
- angle a is the angle of deviation
- AB is the base of the prism.
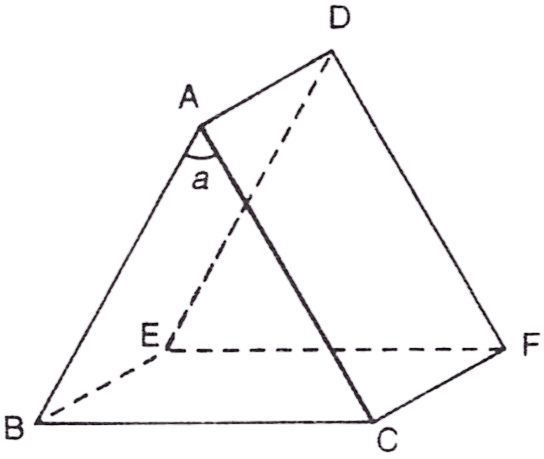
Answer
line AD is the refracting edge
Reason — ABED and ACFD are the refracting surfaces, angle a is the angle of prism and BCFE is the base of the prism.
The angle of prism A is given as:
- r1 - r2
- i1 + i2
- r1 + r2
- r1 / r2
Answer
r1 + r2
Reason — The angle of a prism is typically represented by the sum of its refracting angles, hence, r1 + r2.
The angle of deviation becomes minimum when:
- i1 = r1
- i1 = r2
- i1 = i2
- r2 = i2
Answer
i1 = i2
Reason — The angle of deviation becomes minimum when angle of incidence (i1) becomes equal to the angle of emergence (i2). This phenomenon occurs when the light ray inside the prism is incident at the minimum deviation angle and is known as the angle of minimum deviation.
In position of minimum deviation, the refracted ray inside the prism is ............... to its base:
- normal
- inclined at 45°
- parallel
- none of the above
Answer
parallel
Reason — In position of minimum deviation, the refracted ray inside the prism is parallel to its base.
Mention the incorrect statement:
- The angle of deviation produced by a prism depends on the colour or wavelength of the light used.
- The angle of incidence also affects the angle of deviation produced by the prism.
- In a prism as well as a parallel sided glass slab the emergent ray is parallel to the incident ray with a lateral displacement.
- The angle of deviation of prism is also affected by the material of the prism.
Answer
In a prism as well as a parallel sided glass slab the emergent ray is parallel to the incident ray with a lateral displacement .
Reason — In a parallel-sided glass slab, the emergent ray is parallel to the incident ray without any lateral displacement. However, in a prism, there is a lateral displacement of the emergent ray due to the angle of the prism.
A ray of light is incident normally on the face of an equilateral glass prism. The angle of refraction from the first face of prism is :
- 45°
- 90°
- 60°
- 0°
Answer
0°
Reason — When a ray of light is incident normally (perpendicularly) on a surface, it means the angle of incidence is 0°.
Assertion (A): If the angles of the base of a prism are equal, then in the position of minimum deviation, the refracted ray will pass parallely to the base of the prism.
Reason (R): For minimum deviation, angle of incidence is equal to the angle of emergence.
- Both A and R are true and R is the correct explanation of A
- Both A and R are true and R is not the correct explanation of A
- assertion is false but reason is true
- assertion is true but reason is false
Answer
Both A and R are true and R is the correct explanation of A.
Explanation
Assertion (A) is true. If the angles of the base of a prism are equal, then at minimum deviation condition for prism the angle of incidence is equal to the angle of emergence and the refracted ray inside the prism is parallel to the base of the prism
Reason (R) is true. For the minimum deviation to occur, the angle of incidence must be equal to the angle of emergence. This ensures that the deviation caused by the prism is minimized.
Complete the following sentence:
Angle of deviation is the angle which the ............... ray makes with the direction of ............... ray.
Answer
Angle of deviation is the angle which the emergent ray makes with the direction of incident ray.
State whether the following statement is 'true' or 'false'.
The deviation produced by a prism is independent of the angle of incidence and is same for all the colours of light.
Answer
The statement given above is False.
Reason — The deviation produced by a prism is not independent of the angle of incidence and the deviation is different for different colors of light due to the phenomenon of dispersion, where different wavelengths of light are refracted by different amounts, resulting in the separation of colors. So, the deviation produced by a prism is not the same for all colours of light
How does the angle of minimum deviation produced by a prism change with increase in (i) the wavelength of incident light and (ii) the refracting angle of the prism?
Answer
(i) The angle of minimum deviation produced by a prism decreases with increase in the wavelength of incident light.
(ii) The angle of minimum deviation produced by a prism increases with increase in the refracting angle of the prism.
Write a relation for the angle of deviation (𝛿) for a ray of light passing through an equilateral prism in terms of angle of incidence (i1), angle of emergence (i2) and angle of prism (A).
Answer
The relation between the angle of incident (i1), angle of emergence (i2), angle of prism (A) and angle of deviation (𝛿) for a ray of light passing through an equilateral prism is given by —
𝛿 = (i1 + i2) - A
Name the colour of white light which is deviated
(i) the most,
(ii) the least, on passing through a prism.
Answer
(i) On passing through a prism, violet colour will deviate the most.
(ii) On passing through a prism, red colour will deviate the least
Which of the two prisms, A made of crown glass and B made of flint glass, deviates a ray of light more?
Answer
For a given angle of incidence, the prism with a higher refractive index produces greater deviation than the prism which has a lower refractive index.
As refractive index of flint glass prism (B) is more than a crown glass prism (A) (i.e. μflint > μcrown)
Hence, a flint glass prism (B) produces more deviation than a crown glass prism (A).
Define the term angle of deviation.
Answer
Angle of deviation is the angle between the direction of incident ray and the emergent ray. It is represented by the greek alphabet δ (delta).
How does the deviation produced by a prism depend on
(i) the refractive index of its material, and
(ii) the wavelength of incident light
Answer
(i) For a given angle of incidence, the prism with a higher refractive index produces greater deviation than the prism which has a lower refractive index.
For example — A flint glass prism produces more deviation than a crown glass prism for same refracting angle since μflint > μcrown
(ii) The refractive index of a given transparent medium is different for the light of different colours. It decreases with the increase in the wavelength of light.
Thus, the refractive index of the material of a prism for visible light is maximum for the violet colour and minimum for the red colour.
Consequently, a given prism deviates violet light the most and red light the least.
(i.e. δ violet > δ red since μviolet > μred )
A ray of light incident at an angle of incidence i1 passes through an equilateral glass prism such that the refracted ray inside the prism is parallel to its base and emerges at an angle of emergence i2.
(i) How is the angle of emergence 'i2' related to the angle of incidence 'i1'.
(ii) What can you say about the angle of deviation in such a situation?
Answer
(i) When a ray of light incident at an angle of incidence i1 passes through an equilateral glass prism such that the refracted ray inside the prism is parallel to its base and emerges at an angle of emergence i2 then angle of incidence i1 is equal to the angle of emergence i2.
Hence,
i1 = i2
(ii) When a ray of light incident at an angle of incidence i1 passes through an equilateral glass prism such that the refracted ray inside the prism is parallel to its base and emerges at an angle of emergence i2 then angle of deviation is minimum.
A light ray of yellow colour is incident on an equilateral glass prism at an angle of incidence equal to 48° and suffers minimum deviation by an angle of 36°.
(i) What will be the angle of emergence?
(ii) If the angle of incidence is changed to (a) 30°, (b) 60°, state in each case whether the angle of deviation will be equal to less than or more than 36°?
Answer
(i) As we know that in an equilateral glass prism the ray suffers minimum deviation.
So, angle of incidence i1 is equal to angle of emergence i2
Given, angle of incidence i1 = 48°
Applying the rule given above, we get,
i1 = i2
⇒ i2 = 48°
Hence, angle of emergence i2 = 48°
(ii) (a) As the minimum angle of deviation is 36° for yellow light, at an incident angle of 48° so for any angle of incidence other than 48° the angle of deviation will be more than 36°.
Hence, when the angle of incidence is changed to 30°, the angle of deviation will be more than 36°.
(b) As the minimum angle of deviation is 36° for yellow light, at an incident angle of 48° so for any angle of incidence other than 48° the angle of deviation will be more than 36°.
Hence, when the angle of incidence is changed to 60°, the angle of deviation will be more than 36°.
How does the angle of deviation depend on refracting angle of the prism?
Answer
The angle of deviation (𝛿) increases with increase in the angle of prism (A).
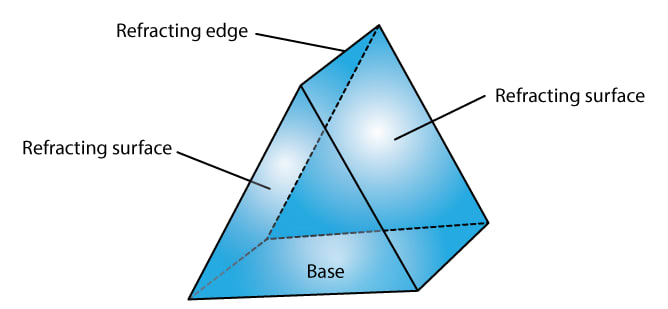
What is a prism? With the help of a diagram of the principal section of a prism, indicate its refracting surfaces, refracting angle and base.
Answer
A prism is defined as a transparent medium bounded by five plane surfaces with a triangular cross section. The below diagram shows the principal section of a prism with its refracting surfaces, refracting angle and base labelled:
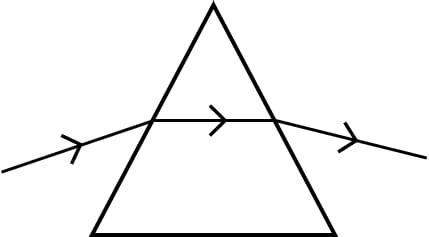
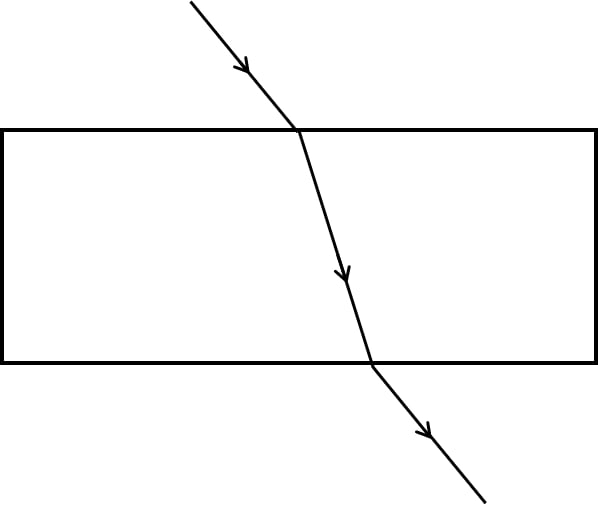
The diagrams (a) and (b) in figure below show the refraction of a ray of light of single colour through a prism and a parallel sided glass slab, respectively.
(a)
(b)
(i) In each diagram, label the incident, refracted, emergent rays and the angle of deviation.
(ii) In what way the direction of the emergent ray in the two cases differ with respect to the incident ray? Explain your answer.
Answer
(i) The below diagram shows the refraction of a ray of light of single colour through a prism with the incident, refracted, emergent rays and the angle of deviation properly labelled:
The below diagram shows the refraction of a ray of light of single colour through a parallel sided glass slab with the incident, refracted, emergent rays and the angle of deviation properly labelled:

(ii) In a prism, the refraction of light occurs at two inclined faces, so the emergent ray is not parallel to the incident ray but it is deviated towards the base of the prism. On the other hand, in a parallel sided glass slab, the refraction of light occurs at two parallel faces, so the emergent ray is parallel to the incident ray with a lateral displacement.
What do you understand by the deviation produced by a prism? Why is it caused? State three factors on which the angle of deviation depends.
Answer
In a prism, the ray of light suffers refraction at two inclined faces. In each refraction, the ray bends towards the base of the prism. The below diagram shows the refraction of a ray of light of single colour through a prism:

At the first face AB, the ray suffers a deviation equal to δ1. Then, at the second face AC, the ray PQ suffers a deviation δ2. Thus, the prism has produced a deviation which is the angle between the direction of incident ray and the emergent ray. This is called the angle of deviation produced by a prism.
The angle of deviation is caused as the ray passing through a prism suffers refraction at two inclined planes.
The three factors on which the angle of deviation depends are as follows:
- The angle of incidence (i)
- The material of prism (i.e on refractive index μ)
- The angle of prism (A)
(a) How does the angle of deviation produced by a prism change with increase in the angle of incidence. Draw a curve showing the variation in the angle of deviation with the angle of incidence at a prism surface.
(b) Using the curve in part (a) above, how would you infer that for a given prism, the angle of minimum deviation 𝛿min is unique for light of a given wavelength.
Answer
(a) It is experimentally observed that as the angle of incidence increases, the angle of deviation first decreases, reaches to a minimum value for a certain angle of incidence and then on further increasing the angle of incidence, the angle of deviation begins to increase. The below curve shows the variation in the angle of deviation with the angle of incidence at a prism surface:
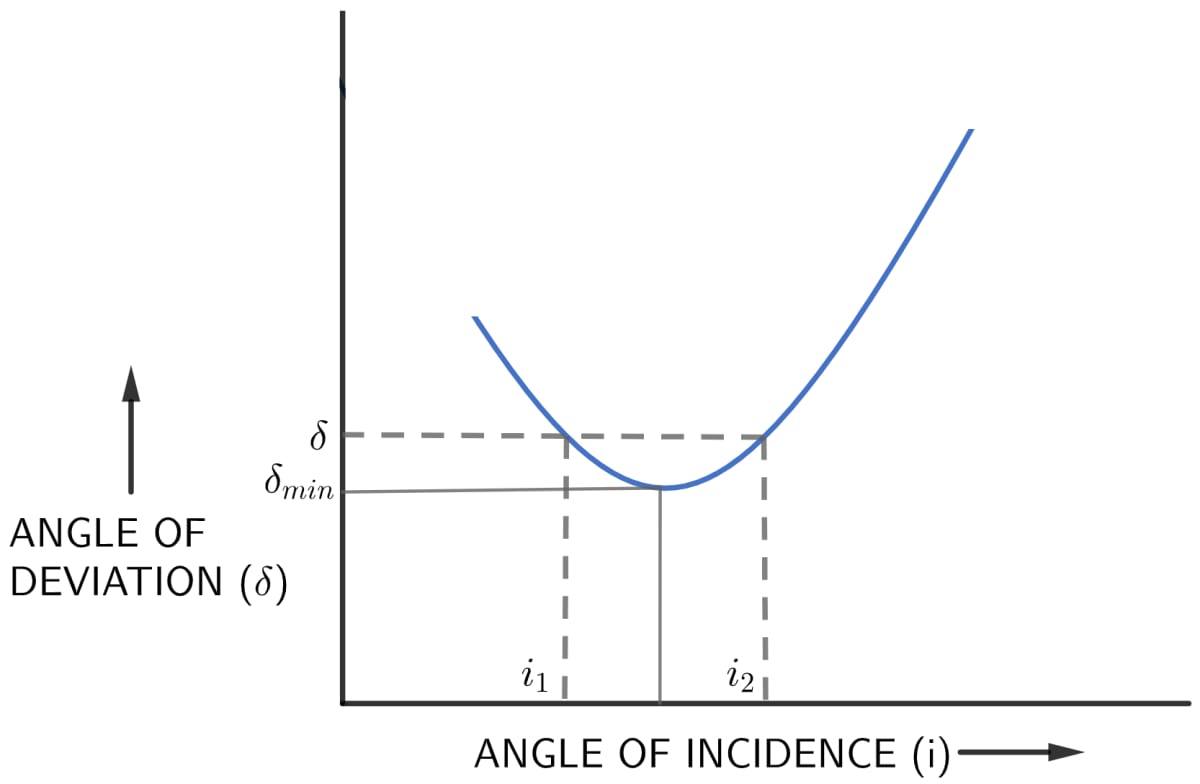
(b) For a given prism and given colour of light, 𝛿min (angle of minimum deviation) is unique since only one horizontal line can be drawn parallel to i – axis at the lowest point of i – 𝛿 curve i.e only for one value of angle of incidence i, the refracted ray inside the prism is parallel to its base.
Draw a ray diagram to show the refraction of a monochromatic ray through a prism when it suffers minimum deviation. How is the angle of emergence related to the angle of incidence in this position.
Answer
Below diagram shows the refraction of a monochromatic light ray through a prism when it suffers minimum deviation:
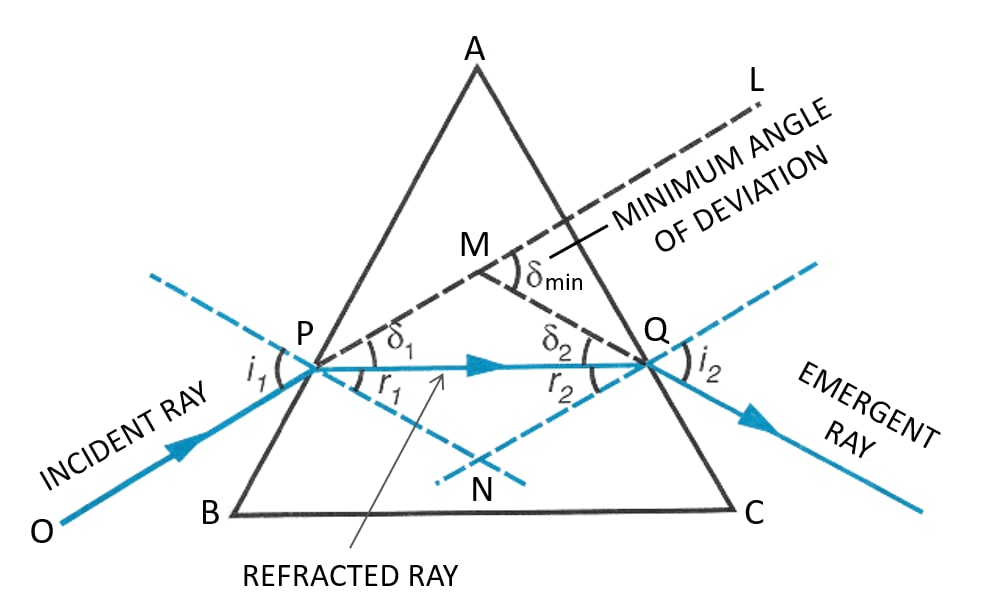
In an equilateral prism, when the prism is in minimum deviation, the angle of incidence i1 is equal to the angle of emergence i2.
Hence,
Angle of emergence (i2) = Angle of incidence (i1).
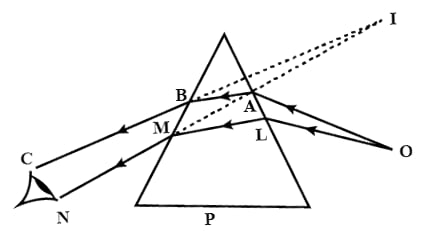
An object is viewed through a glass prism with its vertex pointing upwards. Draw a ray diagram to show the formation of its image as seen by the observer on the other side of the object.
Answer
Below ray diagram shows the formation of the image of an object when seen by an observer through a glass prism with its vertex pointing upwards:
A ray of light is normally incident on one face of an equilateral glass prism.
Answer the following —
(a) What is the angle of incidence on the first face of the prism?
(b) What is the angle of refraction from the first face of the prism?
(c) What will be the angle of incidence at the second face of the prism?
(d) Will the light ray suffer minimum deviation by the prism?
Answer
(a) The angle of incidence on the first face of the prism when a ray of light is normally incident is 0°.
(b) The angle of refraction from the first face of the prism r1 = 0° as the angle of refraction of a normally incident ray is always 0°.
(c) As the prism is equilateral therefore A = 60°.
Given, r1 = 0°.
Hence, taking into consideration the two conditions we get,
the angle of incidence at the second face of the prism, equal to 60°.
(d) No, the light ray will not suffer minimum deviation as the angle of incidence is 0°.
The diagram below shows two identical prisms A and B placed with their faces parallel to each other. A ray of light of single colour PQ is incident at the face of the prism A. Complete the diagram to show the path of the ray till it emerges out of the prism B.
[Hint: The emergent ray out of the prism B will be parallel to the incident ray PQ]
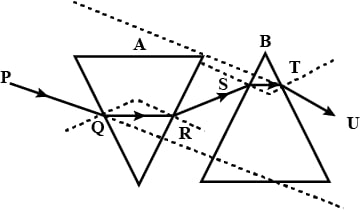
Answer
The below diagram shows the complete path of the ray as it enters prism A and emerges out of prism B:
A ray of light incident at an angle of incidence 48° on a prism of refracting angle 60° suffers minimum deviation. Calculate the angle of minimum deviation. [ Hint — δmin = 2i - A ]
Answer
As we know,
Given,
i = 48°
A = 60°
So, substituting the values in the formula above we get,
Hence, the angle of minimum deviation is equal to 36°
What should be the angle of incidence for a ray of light which suffers minimum deviation of 36° through an equilateral prism?[ Hint — A = 60° and i = ( A + δmin ) / 2 ]
Answer
As we know,
Given,
A = 60°
So, substituting the values in the formula above we get,
Hence, the angle of incidence is equal to 48°.
Refractive index of a liquid can be found using :
- μ = real depth x apparent depth
- μ = apparent depth/real depth
- μ = real depth/apparent depth
- none of the above
Answer
μ = real depth/apparent depth
Reason — Refractive index of a liquid can be found using μ = real depth/apparent depth
A small air bubble in a glass block when seen from above appears to be raised because of:
- refraction of light
- reflection of light
- reflection and refraction of light
- none of the above
Answer
refraction of light
Reason — When you look at a small air bubble in a glass block from above, the light rays coming from the air bubble bend as they pass from the denser medium (glass) to the less dense medium (air). This bending of light causes the apparent position of the air bubble to be shifted, making it appear raised or displaced from its actual position. Therefore, the apparent displacement of the air bubble is due to the refraction of light.
An object in a denser medium when viewed from a rarer medium appears to be raised. The shift is maximum for:
- red light
- violet light
- yellow light
- green light
Answer
violet light
Reason — When light travels from a rarer medium to a denser one, it bends towards the normal. The amount of bending (and consequently the apparent shift in the position of the object) is inversely proportional to the wavelength of light, which is characterized by its color.
This means that shorter wavelengths (such as violet light) will experience a greater degree of refraction compared to longer wavelengths (such as red light).
The shift by which an object appears to be raised depends on:
- the refractive index of the medium
- the thickness of denser medium
- the wavelength of incident light
- all of the above
Answer
all of the above
Reason — The shift by which an object appears raised depends on:
- The refractive index of the medium — higher the refractive index of the medium, more is the shift.
- The thickness of the denser medium — thicker the medium, more is the shift
- Colour of the incident light — the shift decreases with the increase in the wavelength of light used.
An object when placed in a rarer medium and is viewed from a denser medium appears to be at a ............... distance than its real distance.
- smaller
- greater
- same
- cannot say
Answer
greater
Reason — When an object is placed in a rarer medium (like air) and viewed from a denser medium (like water), the light rays coming from object when passing from air to water, bend towards the normal and appear to be coming from a new point such that the distance appears greater than the actual distance.
A glass slab is placed over a piece of paper on which VGYR is printed with letter V in violet, G in green, Y in yellow and R in red colour. The letter of colour ............... appears to be the most raised.
- red
- green
- yellow
- violet
Answer
violet
Reason — The shift increases with the decrease in the wavelength of light used. Since, wavelength of violet light is least, hence, the shift is maximum and it appears to be the most raised.
Assertion (A): The stars twinkle while the planets do not.
Reason (R): Stars are more distant than the planets.
- Both A and R are true and R is the correct explanation of A
- Both A and R are true and and R is not the correct explanation of A
- assertion is false but reason is true
- assertion is true but reason is false
Answer
Both A and R are true and R is the correct explanation of A.
Explanation
Assertion (A) is true. Planets do not twinkle because, unlike stars, they are seen as extended sources of light. When observing a planet, which appears as a disk rather than a point of light, the combined effect of a large number of point-sized sources averages out the total variation in the amount of light entering the observer's eye. This averaging effect nullifies the twinkling phenomenon, making planets appear steady in brightness.
Reason (R) is true. Planets are much closer to us than stars, so they are not point-sized objects to our eye. Hence, the fluctuations have a negligible effect and they don't seem to twinkle.
Assertion (A): An empty test tube placed in water in a beaker with its mouth outside the water surface appears silvery when viewed from a suitable direction.
Reason (R): The substance in water appears silvery due to refraction of light.
- Both A and R are true and R is the correct explanation of A
- Both A and R are true and and R is not the correct explanation of A
- assertion is false but reason is true
- assertion is true but reason is false
Answer
assertion is true but reason is false.
Explanation
Assertion (A) is true. An empty test tube placed in water in a beaker with its mouth outside the water surface appears silvery when viewed from a suitable direction because of the phenomenon of total internal reflection at the air-water interface, which can create a silvery appearance.
Reason (R) is false. Substance in water appears silvery due to the refraction of light, is incorrect. The silvery appearance typically arises due to total internal reflection, not refraction.
Assertion (A): A ray of light travelling from a rarer medium to a denser medium, slows down and bends away from the normal.
Reason (R): The speed of light is higher in a rarer medium than in a denser medium.
- Both A and R are true and R is the correct explanation of A
- Both A and R are true and and R is not the correct explanation of A
- assertion is false but reason is true
- assertion is true but reason is false
Answer
assertion is false but reason is true.
Explanation
Assertion (A) is false. When a ray of light travels from a rarer medium to a denser medium, it slows down and bends towards the normal. This is due to the change in speed and direction of light when it crosses the boundary between two different mediums, which is known as refraction.
Reason (R) is true. The speed of light is higher in a rarer medium (e.g., air) compared to a denser medium (e.g., glass or water). This difference in speed is what causes the refraction of light when it passes from one medium to another.
How is the refractive index of a medium related to the real and apparent depths of an object in that medium?
Answer
The relation of refractive index μ with real and apparent depth is given as below,
An object placed in one medium when seen from the other medium, appears to be vertically shifted. Name two factors on which the magnitude of the shift depends and state how does it depend on them.
Answer
The shift by which the object appears to be raised depends on —
(i) The refractive index of the medium — Higher the refractive index of the medium, more is the shift.
(ii) The thickness of the denser medium — Thicker the medium, more is the shift.
(iii) The colour or wavelength of incident light — the shift decreases with the increase in the wavelength of light used.
Prove that,
Answer
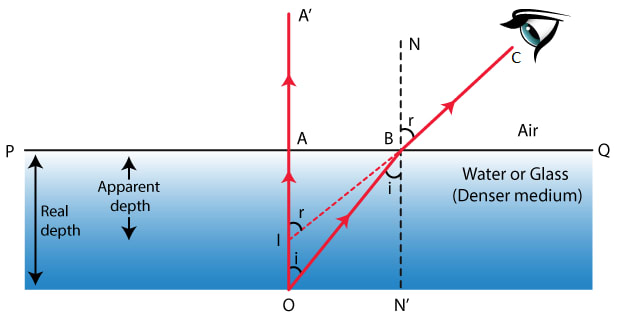
Consider a point object O kept at the bottom of a transparent medium ( such as water or glass ) separated from air by the surface PQ.
A ray of light OA, starting from the object O, is incident on the surface PQ normally, so it passes undeviated along the path AA'. Another ray OB, starting along the object O, strikes the boundary surface PQ at B and suffers refraction.
Since, the ray travels from denser to rarer medium so it bends away from normal N'BN drawn at the point of incidence B on the surface PQ and travels along BC in air.
When viewed by the eye , the ray BC appears to be coming from point I which is the virtual image of O, obtained on producing A'A and CB backwards.
Thus, any point seen from air will appear to be at I, which is lesser depth = AI than its actual depth AO.
Angle of incidence = ∠OBN'
Angle of refraction = ∠CBN.
Since, AO and BN’ are parallel and OB is transversal line, so
∠AOB = ∠OBN' = i
Similarly, IA’ and BN are parallel and IC is the transversal line, so
∠BIA’ = ∠CBN = r
In right-angle triangle BAO,
and,
In right-angle triangle IAB,
For refraction from medium to air, by Snell’s law
Hence, refractive index of medium with respect to air is,
The object is viewed from a point vertically above the object O, since point B is very close to the point A. ∴ IB = IA and OB = OA
Hence,
A tank of water is viewed normally from above.
(a) State how does the depth of tank appears to change.
(b) Draw a labelled ray diagram to explain your answer.
Answer
(a) When a tank is viewed normally from above from a rarer medium, the apparent depth of the tank is always less than its real depth.
As aμw = 4 / 3, therefore, the depth of the pond appears three fourth of its real depth on seeing it from air in a nearly vertical direction.
(b) Below is the labelled ray diagram of a tank of water viewed normally from above:

Water in a pond appears to be only three-quarters of its actual depth.
(a) What property of light is responsible for this observation? Illustrate your answer with the help of a ray diagram.
(b) How is the refractive index of water calculated from its real and apparent depths?
Answer
(a) Water in a pond appears to be only three-quarters of its actual depth due to the refraction of light while travelling from one medium to another.
The light rays suffer refraction while travelling from denser medium (water or glass) to rarer medium (air), so it bends away from the normal. Below is the ray diagram for this:
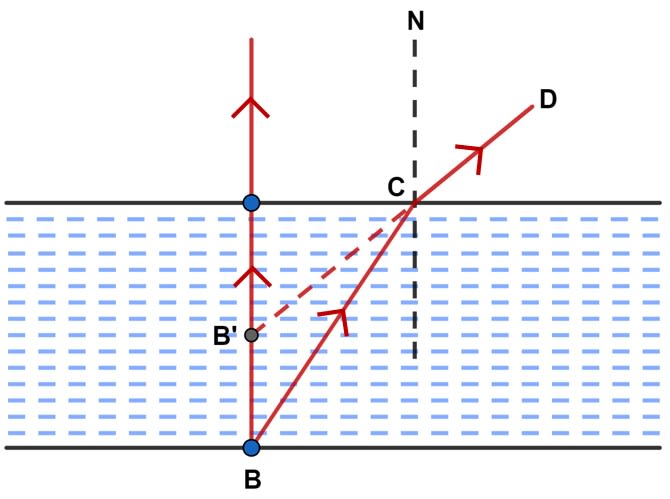
(b) Let us say an object (B) is at the bottom of a pond. Consider a ray of light BC from the object that moves from water to air.
The ray now moves away from the normal N along the path CD, after refraction from the water surface.
When we produce CD it appears from the point B’.
The virtual image of the object B appears at B’.
Hence, we get,
Draw a ray diagram to show the appearance of a stick partially immersed in water. Explain your answer.
Answer
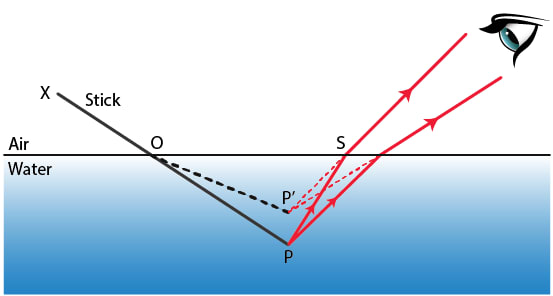
The above figure shows a stick placed obliquely in water. The portion OP of the stick under water when seen from air appears to be shortened and raised up as OP'. This is due to refraction of light from water to air.
The rays of light coming from tip P of the stick when pass from water to air, bend away from the normal and appear to be coming from point P' which is the virtual image of the point P.
Thus, the part PO of the stick appears to be P'O.
Hence, the immersed part of the stick appears to be raised and therefore, bent at the point O at the surface of water and the stick XOP appears as XOP'.
A fish is looking at a 1.0 m high plant at the edge of a pond. Will the plant appear to the fish shorter or taller than its actual height? Draw a ray diagram to support your answer.
Answer
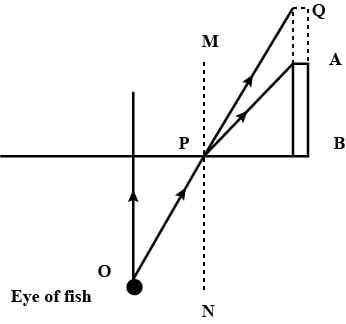
When a fish is looking at a 1.0 m high plant at the edge of the pond, it appears to be taller than its actual height due to the refraction of the light rays travelling from one medium to another.
When the fish is looking at the plant, as air is a rarer medium in comparison to water, the ray OP will bend away from the normal while emerging out from the water to air.
But, when we extend the ray it appears to be coming from a higher point.
Hence, the plant will look taller than its actual height.
A student puts his pencil into an empty trough and observes the pencil from the position as indicated in the figure.
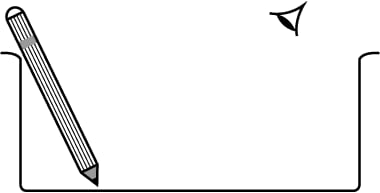
(i) What change will be observed in the appearance of the pencil when water is poured into the trough?
(ii) Name the phenomenon which accounts for the above-started observation.
(iii) Complete the diagram showing how the student’s eye sees the pencil through water.
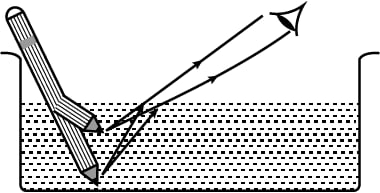
Answer
(i) When a student puts his pencil into an empty trough, and later pours water in the same trough, the part of the pencil which is immersed in water will look short and raised up.
(ii) The above observation is based on the phenomenon of refraction of light.
(iii) Below is the diagram showing how the student’s eye sees the pencil through water:
A water pond appears to be 3 m deep. If the refractive index of water is 4/3, find the actual depth of the pond.
Answer
We know that,
Real depth = Apparent depth x Refractive index of water
Given,
Apparent depth = 3 m
Refractive index of the water =
So, substituting the values in the formula we get,
Real depth =
Hence, actual depth = 4 m
A coin is placed at the bottom of a beaker containing water (refractive index = 4/3) at a depth of 16 cm. By what height the coin appears to be raised when seen from vertically above?
Answer
As we know,
Given,
and
Real depth = 16 cm
So, substituting the values in the formula we get,
Hence, the coin appears to be raised by a height of 4 cm when seen from vertically above.
A postage stamp kept below a rectangular glass slab of refractive index 1.5 when viewed from vertically above it, appears to be raised by 7.0 mm. Calculate the thickness of the glass slab.
Answer
As we know,
Given,
Shift in the image = 7 mm or 0.7 cm
Refractive index of the glass block = 1.5
So, substituting the values in the formula we get,
Hence, the thickness of glass slab = 2.1 cm.
(Thickness of glass slab is same as the real depth of the postage stamp).
At angle of incidence equal to the critical angle, the angle of refraction is:
- 0°
- 30°
- 90°
- 180°
Answer
90°
Reason — When light travels from a denser medium to a rarer medium and the angle of incidence is equal to the critical angle, the angle of refraction becomes 90° as shown in the below fig:
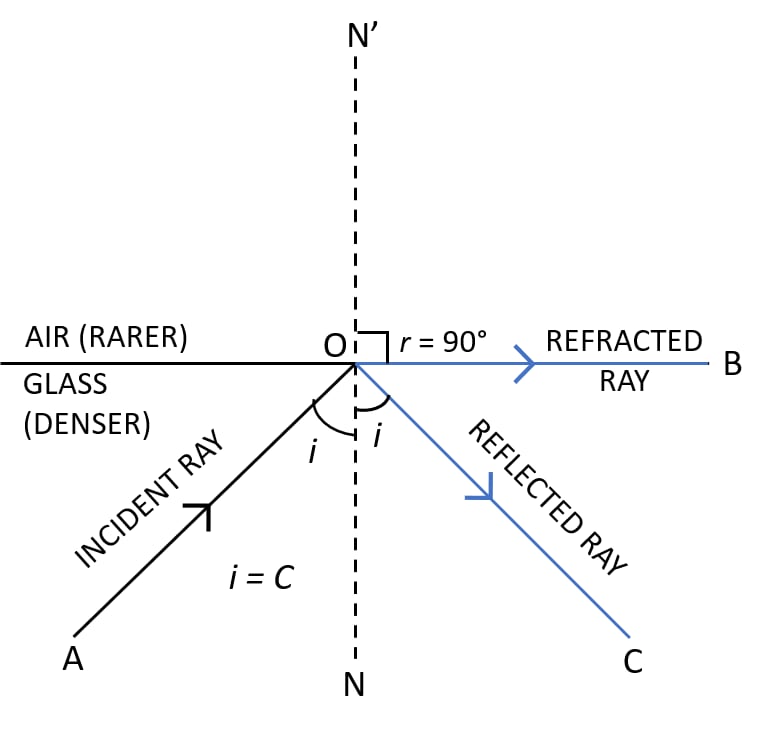
The condition required for total internal reflection to take place is:
- light ray passes from a rarer to denser medium
- light ray passes from a denser to rarer medium
- angle of incidence is less than critical angle
- none of the above
Answer
light ray passes from a denser to rarer medium
Reason — The two necessary conditions for total internal reflection are —
- The light must travel from a denser medium to a rarer medium.
- The angle of incidence must be greater than the critical angle for the pair of media.
A scientist while performing an experiment desires that no incident light escapes from the top of a glass block. He varies the angle X continuously and finally manages to achieve his objective. Which of the following options describes the correct answer?
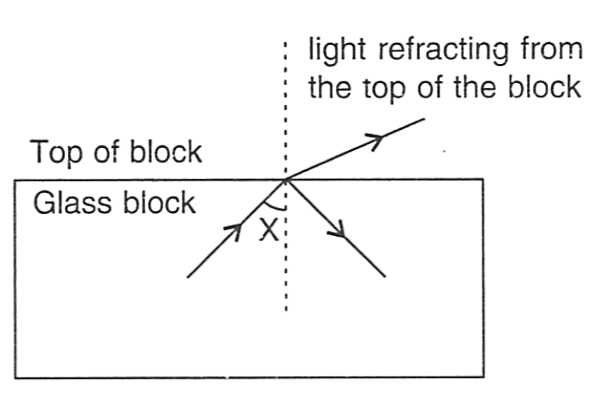
| Angle | Effect Produced | |
|---|---|---|
| (a) | Decreased | Total Internal Reflection |
| (b) | Decreased | Total Internal Refraction |
| (c) | Increased | Total Internal Refraction |
| (d) | Increased | Total Internal Reflection |
- Option (a)
- Option (b)
- Option (c)
- Option (d)
Answer
Option (d)
Reason — As a ray travels from denser medium to rarer medium and if it's angle of incidence is greater than the critical angle then total internal reflection occurs so scientist must increase angle X till it beocmes greater than the critical angle to achieve total internal reflection.
When a ray of light travels from substance A to substance B and reaches their boundary, it suffers total internal reflection. Out of the following possibilities, which one is correct?
| Angle i | Substance B | |
|---|---|---|
| (a) | i < C | Optical density of A is less than B |
| (b) | i = C | Optical density of A is more than B |
| (c) | i > C | Optical density of A is less than B |
| (d) | i > C | Optical density of A is more than B |
- Option (a)
- Option (b)
- Option (c)
- Option (d)
Answer
Option (d)
Reason — There are two necessary conditions for total internal reflection :
The light must travel from an optically denser to a rarer medium.
The angle of incidence must be greater than the critical angle for the pair of media.
An equilateral prism can be used to deviate a ray of light through:
- 30°
- 60°
- 75°
- 90°
Answer
60°
Reason — An equilateral prism can be used to deviate a ray of light through 60°.
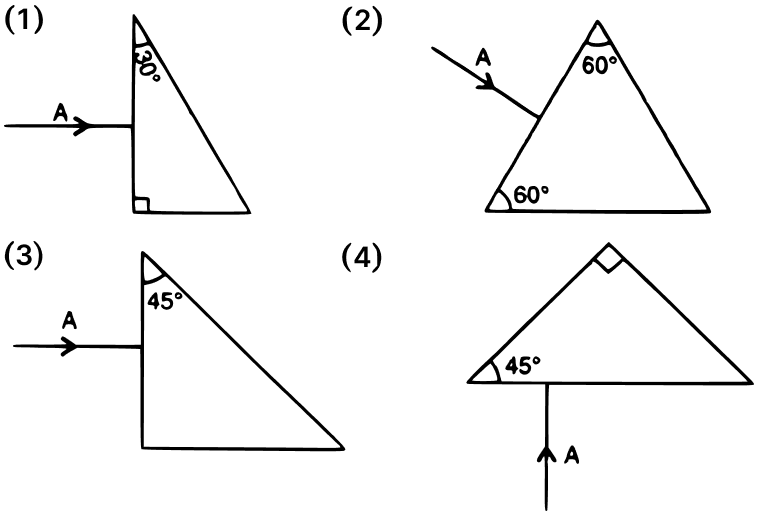
Which of the following figures will depict deviation of ray of light A through 180°
Answer
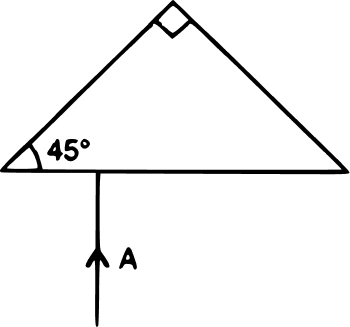
Reason — Below is the completed diagram showing the deviation of ray of light A through 180°:
The diagram below shows a light source P embedded in a rectangular glass block ABCD of critical angle 42°. The ray PQ would:
![The diagram below shows a light source P embedded in a rectangular glass block ABCD of critical angle 42°. Complete the path of the ray PQ till it emerges out of the block. [Write necessary angles.] ICSE 2019 Physics Solved Question Paper.](https://cdn1.knowledgeboat.com/img/abp10/5/icse-2019-physics-question-paper-solved-2e-1200x730.png)
- pass undeviated
- suffer refraction
- suffer reflection
- suffer total internal reflection
Answer
suffer total internal reflection
Reason — We can see from the below diagram that the ray is travelling from a denser to a rarer medium and the angle of incidence is greater than the critical angle. In such a case no refracted ray is obtained and the incident ray is reflected back into the same medium. This phenomenon is known as total internal reflection.
![The diagram below shows a light source P embedded in a rectangular glass block ABCD of critical angle 42°. Complete the path of the ray PQ till it emerges out of the block. [Write necessary angles]. ICSE 2019 Physics Solved Question Paper.](https://cdn1.knowledgeboat.com/img/abp10/5/icse-2019-physics-question-paper-solved-2e-completed-diagram-1200x821.png)
In the process of total internal reflection, ............... of energy (or intensity) of light is reflected back.
- 70%
- 80%
- 100%
- 50%
Answer
100%
Reason — In the process of total internal reflection, all of the light is reflected back into the original medium, and none of the energy (or intensity) of the light is lost. Therefore, 100% of the energy of the light is reflected back.
Out of violet, blue, yellow and red, the critical angle would be the least for ............... light for a pair of media.
- violet
- blue
- blue
- yellow
Answer
violet
Reason — Critical angle is inversely proportional to the refractive index, μViolet > μRed, hence critical angle would be least for violet light for a pair of media.
How is the critical angle related to the refractive index of a medium?
Answer
Knowing the refractive index of the denser medium with respect to the rarer medium, we can calculate the critical angle C for that pair of medium with the help of the relation
State the approximate value of the critical angle for
(a) glass-air surface
(b) water-air surface.
Answer
(a) As we know,
Refractive index is
Substituting the values in the formula we get,
As,
Hence, critical angle for glass air surface is 42°.
(b) As we know,
Refractive index is
Substituting the values in the formula we get,
Hence, critical angle for water air surface is 49°.
A light ray is incident from a denser medium on the boundary separating it from a rarer medium at an angle of incidence equal to the critical angle. What is the angle of refraction for the ray?
Answer
The angle of refraction becomes equal to 90° when a light ray is incident from a denser medium on the boundary separating it from a rarer medium at an angle of incidence equal to the critical angle. Below diagram shows the path of the ray when angle of incidence is equal to the critical angle:

The critical angle for glass-air is 45° for the light of yellow colour. State whether it will be less than, equal to, or more than 45° for
(i) red light,
(ii) blue light ?
Answer
As the wavelength of light decreases (or increases) refractive index becomes more (or less) and critical angle becomes less (or more).
(i) As the wavelength for red light is more than that for yellow colour, the refractive index becomes less and the critical angle will be more than 45°.
(ii) As the wavelength for blue light is less than that for yellow colour, the refractive index becomes more and the critical angle will be less than 45°.
Which colour of light has higher critical angle ? Red light or green light.
Answer
As we know, the relation between critical angle and refractive index is
where, c is critical angle and μ is refractive index.
As μ for red light is less as compared to that for green light and μ and c are inversely related.
Hence, the critical angle of red light is higher than that of green light.
Fill in the blanks to complete the following sentences —
(a) Total internal reflection occurs only when a ray of light passes from a ............... medium to a ............... medium.
(b) Critical angle is the angle of ............... in denser medium for which the angle of ............... in rarer medium is ...............
Answer
(a) Total internal reflection occurs only when a ray of light passes from a denser medium to a rarer medium.
(b) Critical angle is the angle of incidence in denser medium for which the angle of refraction in rarer medium is 90°.
State whether the following statement is true or false —
If the angle of incidence is greater than the critical angle, light is not refracted at all, when it falls on the surface from a denser medium to a rarer medium.
Answer
True
Reason — When the angle of incidence is greater than the critical angle, light undergoes total internal reflection and effectively remain within the denser medium. Hence, no refracted ray is obtained.
What is meant by the statement 'the critical angle for diamond is 24°'?
Answer
The statement 'the critical angle for diamond is 24°' implies that at an incident angle of 24°, the angle of refraction in the air will be 90° within the diamond.
If the incident angle is more than the critical angle then the ray will suffer total internal reflection without any refraction.
Name two factors which affect the critical angle for a given pair of media. State how do the factors affect it.
Answer
The critical angle depends on two factors:
(a) The colour or wavelength of light — The refractive index of a transparent medium decreases with the increase of wavelength of light. (It is most for violet light and least for red light), therefore the critical angle for a pair of media is least for the violet light and most for the red light, i.e. the critical angle increases with the increase in wavelength of light.
(b) The temperature — On increasing the temperature of medium, its refractive index decreases. So, the critical angle for the pair of medium increases with increase in temperature.
The refractive index of air with respect to glass is expressed as
(a) Write down a similar expression for aμg in terms of the angles i and r.
(b) If angle r = 90°, what is the corresponding angle i called?
(c) What is the physical significance of the angle i in part (b)?
Answer
(a) The expression for aμg =
(b) When refractive angle r = 90° then, the corresponding angle of incidence i will be equal to critical angle.
(c) The phenomenon of total internal reflection occurs when the angle of incidence exceeds the value of i obtained in part (b).
The table below gives refractive inidices of some substances with respect to air.
| Substance | Refractive Index (μ) |
|---|---|
| Water | 1.33 |
| Turpentine | 1.47 |
| Glass | 1.58 |
| Diamond | 2.41 |
(a) Which medium will have the lowest critical angle and which will have highest critical angle with respect to air.
(b) If the temperature of all the substances is raised by 30o C, what will happen to their critical angle?
Answer
(a) Diamond has lowest critical angle and water has highest critical angle.
(b) If the temperature of all the substance is raised by 30o C then the critical angle of the all the media will increase.
Reason :
(a) As the relation between critical angle and refractive index of a medium is given by,
where is the refractive index of the given medium with respect to air
From above relation it is clear that critical angle (C) has inverse relation with refractive index () so lowest C is the one with highest value of and similarly highest C value corresponds to lowest .
(b) On increasing the temperature of a medium, it's refractive index decreases, therefore the critical angle increases with the increase in temperature.
Mention one difference between the reflection of light from a plane mirror and total internal reflection of light from a prism.
Answer
| Plane mirror | Prism |
|---|---|
| In reflection of light from a plane mirror, only a part of the light is reflected while rest is refracted and absorbed. So, the reflection is partial. | In total internal reflection of light from a prism, the entire incident light is reflected back into the denser medium. So there is no loss of light energy. |
State one advantage of using a total reflecting prism as a reflector in place of a plane mirror.
Answer
The advantage of using a total reflecting prism as a reflector in place of a plane mirror, is that the image is much brighter and the brightness remains unchanged even after the long use of the total reflecting device.
In the case of a plane mirror, the image is less bright and the brightness gradually decreases as the silvering on mirror becomes old and rough.
Explain the term critical angle with the aid of a labelled diagram.
Answer

When a ray of light passes from a denser to a rarer medium, at a certain angle of incidence i = C, the angle of refraction becomes 90°.
This angle C is called the critical angle.
Thus, critical angle is defined as the angle of incidence in the denser medium corresponding to which the angle of refraction in the rarer medium is 90°.
(a) What is total internal reflection?
(b) State two conditions necessary for total internal reflection to occur.
(c) Draw diagram to illustrate total internal reflection.
Answer
(a) When a ray of light travelling in a denser medium, is incident at the surface of a rarer medium at the angle of incidence greater than the critical angle for the pair of media, the ray is totally reflected back into the denser medium. This phenomenon is known as total internal reflection.
(b) The two necessary conditions for total internal reflection are —
- The light must travel from a denser medium to a rarer medium.
- The angle of incidence must be greater than the critical angle for the pair of media.
(c) Below diagram illustrate total internal reflection:
Total Internal Reflection Diagram:
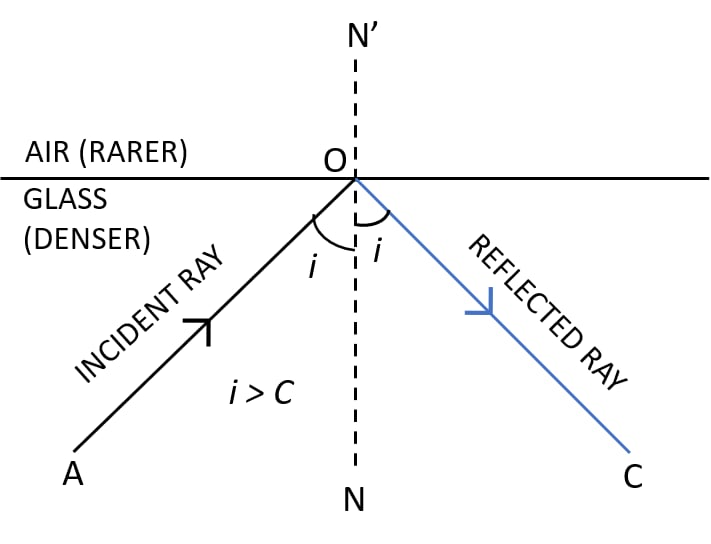
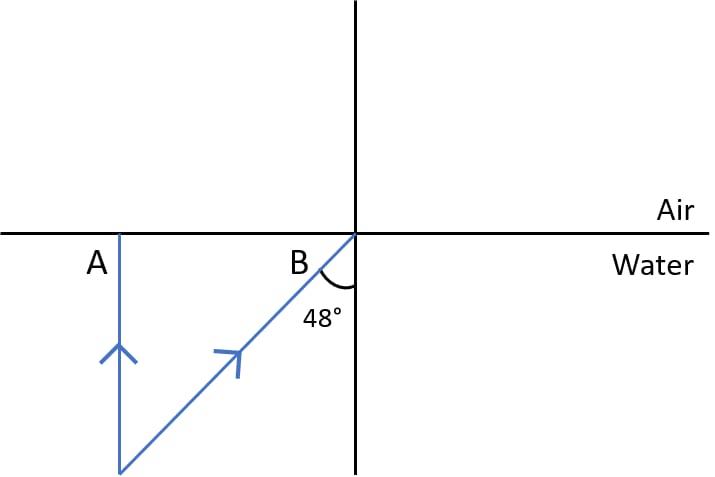
Figure below shows two rays A and B travelling from water to air. If the critical angle for water-air surface is 48°, complete the ray diagram showing the refracted rays for each. State conditions when the ray will suffer total internal reflection.
Answer
Completed ray diagram with refracted rays labelled is shown below:
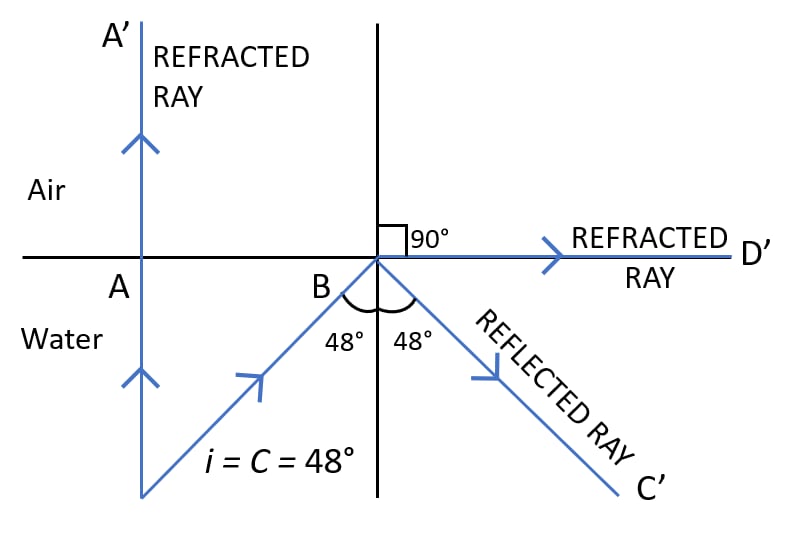
Ray A is incident normally at water air boundary so its angle of incidence is 0°. Hence, the refracted ray shown as AA' in the diagram passes undeviated.
For Ray B, the angle of incidence is equal to the critical angle for water air boundary so it is partly reflected as BC' and partly refracted as BD'.
Two necessary conditions for the total internal reflection are —
- The light must travel from a denser to a rarer medium.
- The angle of incidence must be greater than the critical angle for the pair of medium.
Figure shows a point source P inside a water container. Three rays A, B and C starting from the source P are shown up to the water surface.
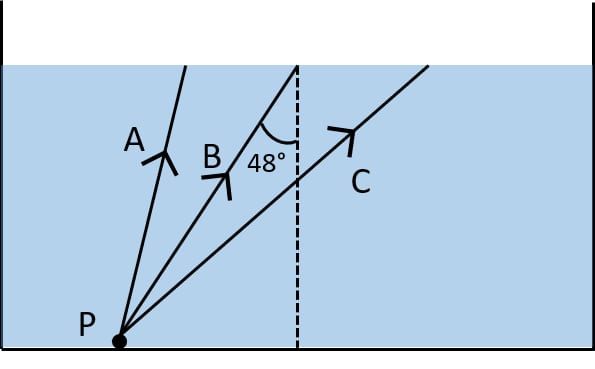
(a) Show in the diagram, the path of these rays after striking the water surface. The critical angle for water-air surface is 48°.
(b) Name the phenomenon which the rays A, B and C exhibit.
Answer
(a) Below diagram shows the path of the rays after striking the water surface:
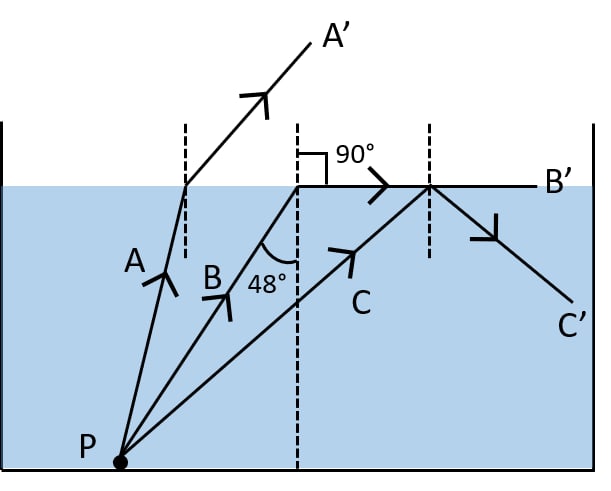
(b) Rays A and B show the phenomenon of ‘refraction of light’ and ray C shows the phenomenon of ‘total internal reflection’.
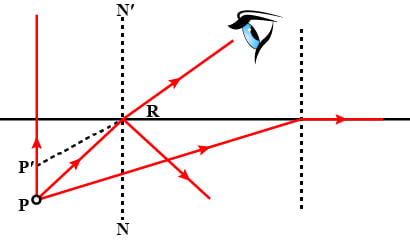
In the figure, PQ and PR are the two light rays emerging from an object P. The ray PQ is refracted as QS.
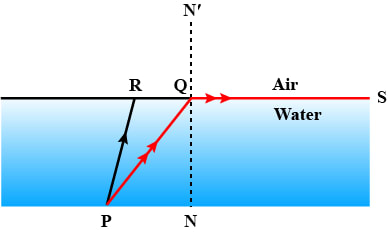
(a) State the special name given to the angle of incidence ∠PQN of the ray PQ.
(b) What is the angle of refraction for the refracted ray QS?
(c) Name the phenomenon that occurs if the angle of incidence ∠PQN is increased.
(d) The ray PR suffers partial reflection and refraction on the water-air surface. Give reason.
(e) Draw in the diagram the refracted ray for the incident ray PR and hence show the position of image of the object P by the letter P' when seen vertically from above.
Answer
(a) The angle of incidence ∠PQN is known as the critical angle.
(b) For the refracted ray QS, the angle of refraction is 90°.
(c) When the angle of incidence ∠PQN is increased, then the phenomenon that occurs is total internal reflection.
(d) For the ray PR, the angle of incidence is less than ∠PQN ( i.e the critical angle ). So according to the laws of reflection, ray PR suffers partial reflection and refraction.
(e) Below diagram shows the refracted ray and the position of image of the object P when seen vertically from above:
The refractive index of glass is 1.5. From a point P inside a glass slab, draw rays PA, PB and PC incident on the glass-air surface at an angle of incidence 30°, 42° and 60° respectively.
(a) In the diagram show the approximate direction of these rays as they emerge out of the slab.
(b) What is the angle of refraction for the ray PB?
(Take sin 42° = 2 / 3)
Answer
(a) Diagram with rays PA, PB and PC is shown below:
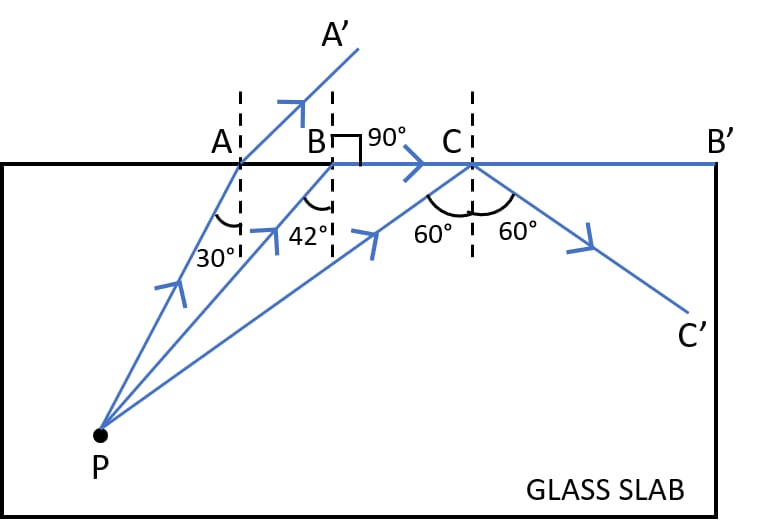
(b) Given,
μg = 1.5
As we know,
Substituting the values in the formula we get,
Hence, we can round off ic = 42°
Applying,
Given,
and
Substituting the values in the formula we get,
As sin r = 1 , so angle of refraction = 90°.
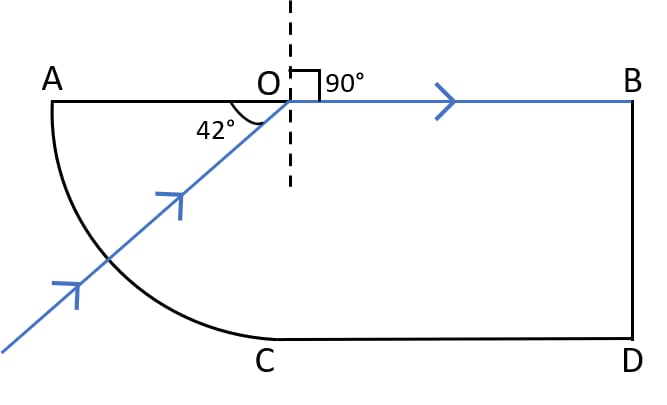
A ray of light enters a glass slab ABDC as shown in figure and strikes at the centre O of the circular part AC of the slab. The critical angle of glass is 42°. Complete the path of the ray till it emerges out from the slab. Mark the angles in the diagram wherever necessary.
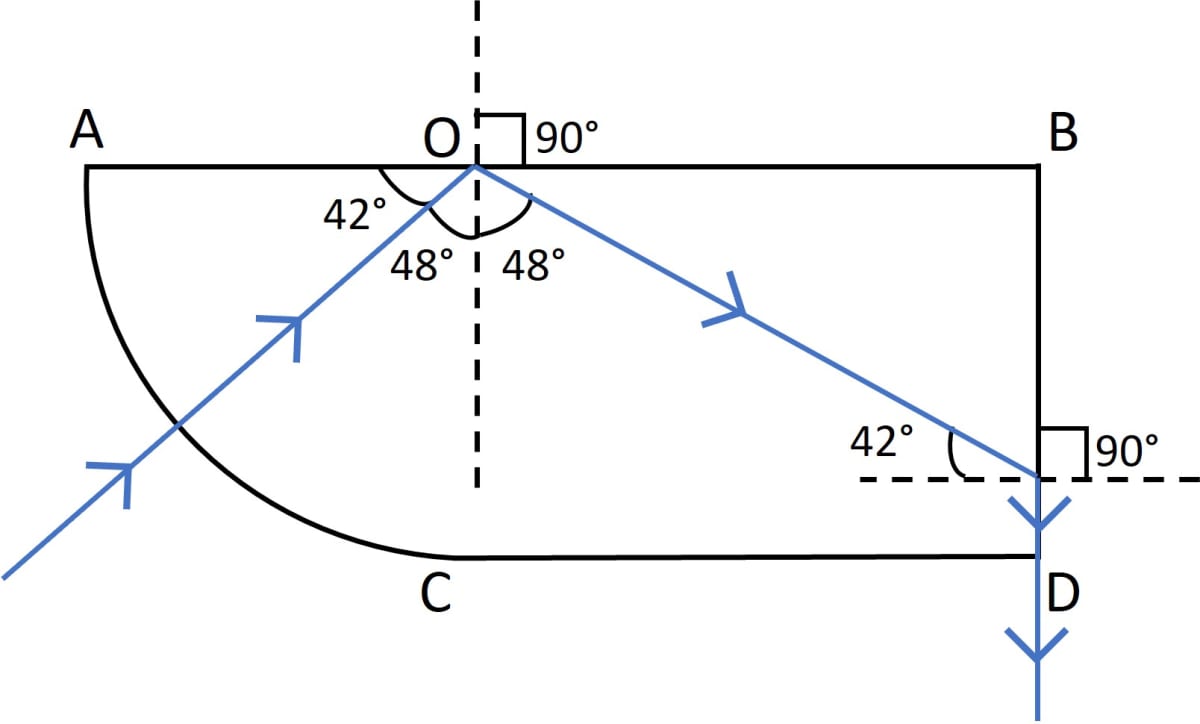
Answer
Completed diagram showing the path of the ray till it emerges out from the slab is shown below:
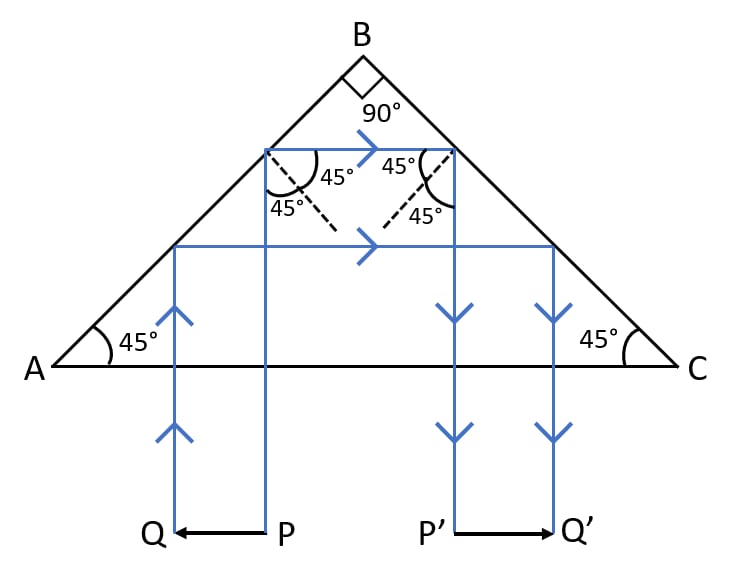
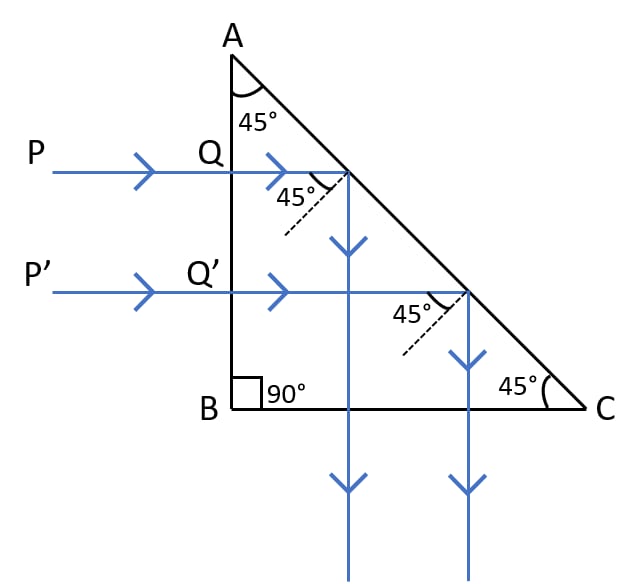
What is a total reflecting prism? State three actions that it can produce. Draw a diagram to show one such action of the total reflecting prism.
Answer
A prism having an angle of 90° between its two refracting surfaces and the other two angles each equal to 45° is called a total reflecting prism. In such a prism, the light incident normally on any of its faces suffers total internal reflection inside the prism.
Due to this property, a total reflecting prism is used for the following three purposes —
- To deviate a ray of light through 90°.
- To deviate a ray of light through 180°.
- To erect the inverted image without producing deviation in its path.
Below diagram shows the deviation of a ray of light through 90° by a total reflecting prism:
Show with the help of a diagram how a total reflecting prism can be used to turn a ray of light through 90°. Name one instrument in which such a prism is used.
Answer
Below diagram shows the deviation of a ray of light through 90° by a total reflecting prism:

ABC is a total reflecting prism. A beam of light is incident normally at the face AB. It passes undeviated into the prism and strikes at the face AC making an angle of incidence equal to 45°.
For glass air interface, the critical angle is equal to 42°, therefore the beam of light suffers total internal reflection at the face AC because the angle of incidence is greater than the critical angle.
The reflected beam inside the prism then strikes the face BC, where it is incident normally and therefore passes undeviated. Hence, the incident beam gets deviated through 90°.
This action of prism is used in a periscope where a total reflecting prism is preferred over a plane mirror.
A ray of light XY passes through a right-angled isosceles prism as shown in the adjacent diagram.
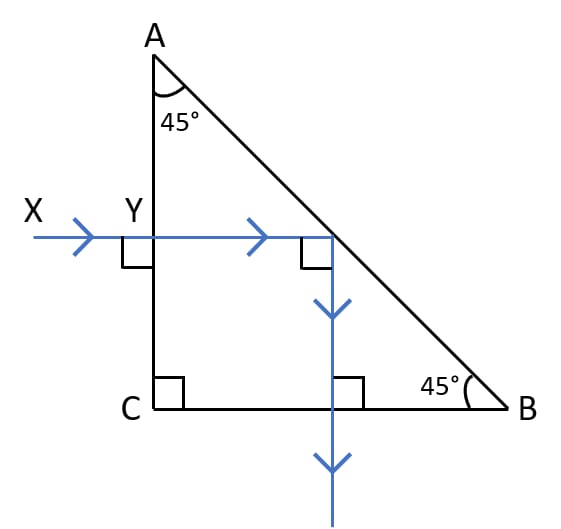
(a) What is the angle through which the incident ray deviates and emerges out of the prism?
(b) Name the instrument where this action of prism is put into use.
(c) Which prism surface will behave as a mirror?
Answer
(a) The angle through which the incident ray deviates and emerges out of the prism is the angle of deviation.
The angle of deviation = the angle which the emergent ray makes with the incident ray XY = 90°.
(b) The instrument where this action of prism is put into use is the periscope.
(c) The surface AB of the prism behaves as a mirror.
Draw a diagram of a right angled isosceles prism which is used to make an inverted image erect.
Answer
Below diagram shows the usage of a right angled isosceles prism which is used to make an inverted image erect:
This action of prism is used in a slide.
In the figure, a ray of light PQ is incident normally on the hypotenuse of an isosceles right angled prism ABC.
(a) Complete the path of the ray PQ till it emerges from the prism. Mark in the diagram the angle wherever necessary.
(b) What is the angle of deviation of the ray PQ?
(c) Name a device in which this action is used.
Answer
(a) Below diagram shows the path of the ray PQ till it emerges from the prism with all the angles labelled:

(b) The angle of deviation of the ray PQ is 180°.
(c) This action of the prism is used in Binoculars.
In the figure given below, a ray of light PQ is incident normally on the face AB of an equilateral glass prism. Complete the ray diagram showing its emergence into air after passing through the prism. Take critical angle for glass = 42°.
(a) Write the angles of incidence at the faces AB and AC of the prism.
(b) Name the phenomenon which the ray of light suffers at the face AB, AC and BC of the prism.
Answer
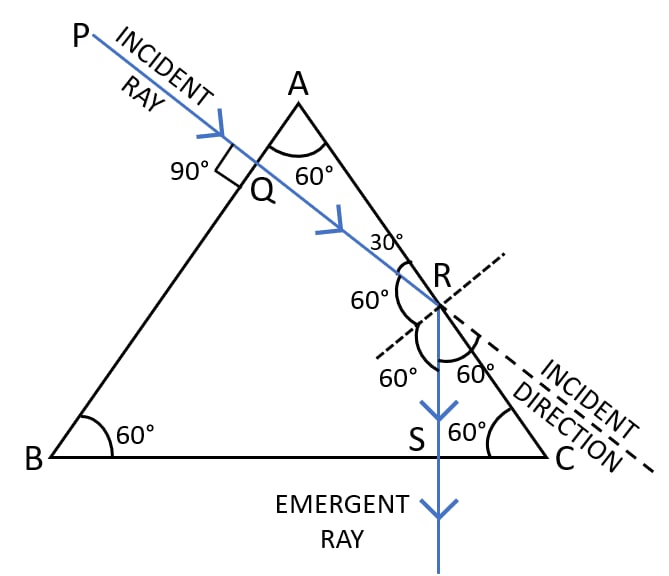
(a) The angle of incidence at the faces AB, i = 0°.
The angle of incidence at the faces AC, i = 60°.
(b) The phenomenon which the ray of light suffers at:
face AB — refraction
face AC — total internal reflection
face BC — refraction
Draw a neat labelled ray diagram to show total internal reflection of a ray of light incident normally on one face of a 30°, 90°, 60° prism.
Answer
Below is the labelled ray diagram showing total internal reflection of a ray of light incident normally on one face of a 30°, 90°, 60° prism
Copy the diagram given below and complete the path of the light ray till it emerges out of the prism. The critical angle of glass is 42°. In your diagram mark the angles wherever necessary.
Answer
Below is the completed diagram showing the path of the light ray till it emerges out of the prism with all angles marked:
What device other than a plane mirror, can be used to turn a ray of light through 180°? Draw a diagram in support of your answer. Name an instrument in which this device is used.
Answer
A total reflecting prism is used to turn a ray of light through 180°.

This device is used in a binocular and camera to invert the image without the loss of intensity.
Two isosceles right-angled glass prisms P and Q are placed near each other as shown in figure. Complete the path of the light ray entering the prism P till it emerges out of the prism Q.
Answer
Below diagram shows the path of the light ray entering the prism P till it emerges out of the prism Q:

Complete the path of ray PQ through the glass prism ABC as shown in figure till it emerges out of the prism. Given the critical angle of glass is 42°.
Answer
Below diagram shows the path of ray PQ through the glass prism ABC till it emerges out of the prism:
The diagram below shows a light source P embedded in a rectangular glass block ABCD of critical angle 42°. Complete the path of ray PQ till it emerges out of the block. [Write necessary angles]
![The diagram below shows a light source P embedded in a rectangular glass block ABCD of critical angle 42°. Complete the path of the ray PQ till it emerges out of the block. [Write necessary angles.] ICSE 2019 Physics Solved Question Paper.](https://cdn1.knowledgeboat.com/img/abp10/5/icse-2019-physics-question-paper-solved-2e-1200x730.png)
Answer
Completed diagram showing the path of the ray PQ till it emerges out of the block is shown below:
![The diagram below shows a light source P embedded in a rectangular glass block ABCD of critical angle 42°. Complete the path of the ray PQ till it emerges out of the block. [Write necessary angles]. ICSE 2019 Physics Solved Question Paper.](https://cdn1.knowledgeboat.com/img/abp10/5/icse-2019-physics-question-paper-solved-2e-completed-diagram-1200x821.png)