State whether the following statements are always true, always false or ambiguous. Justify your answers.
(i) All mathematics textbooks are interesting.
(ii) The distance from the Earth to the Sun is approximately 1.5 × 108 km.
(iii) All human beings grow old.
(iv) The journey from Uttarkashi to Harsil is tiring.
(v) The woman saw an elephant through a pair of binoculars.
Answer
(i) This statement is ambiguous, because we cannot decide if it is always true or always false. One book can be interesting for a person and another book for another person.
(ii) This statement is always true as astronomers have established that the distance from the Earth to the Sun is approximately 1.5 × 108 km.
(iii) This statement is always true since every human being grows old as time passes.
(iv) This statement is ambiguous, because whether the journey is tiring or not depends on how the journey was completed and will vary from person to person.
(v) This statement is ambiguous, because we don't know which woman the statement is referring to.
State whether the following statements are true or false. Justify your answers.
(i) All hexagons are polygons.
(ii) Some polygons are pentagons.
(iii) Not all even numbers are divisible by 2.
(iv) Some real numbers are irrational.
(v) Not all real numbers are rational.
Answer
(i) This statement is true as in geometry a hexagon can be defined as a closed two-dimensional polygon with six sides.
(ii) This statement is true as not all polygons are pentagons.
(iii) This statement is false because every even number is divisible by 2.
(iv) This statement is true because not all real numbers are irrational.
(v) This statement is true because this statement is the same as saying "there is a real number that is irrational". As we know, real numbers can be irrational as well. Hence, the statement is true.
Let a and b be real numbers such that ab ≠ 0. Then which of the following statements are true? Justify your answers.
(i) Both a and b must be zero.
(ii) Both a and b must be non-zero.
(iii) Either a or b must be non-zero.
Answer
The true statement is:
Both a and b must be non-zero.
Reason — If the product of two numbers is non-zero, then both the numbers must be non-zero.
Restate the following statements with appropriate conditions, so that they become true.
(i) If a2 > b2, then a > b.
(ii) If x2 = y2, then x = y.
(iii) If (x + y)2 = x2 + y2, then x = 0.
(iv) The diagonals of a quadrilateral bisect each other.
Answer
(i) If a > 0 and a2 > b2, then a > b.
(ii) If xy ≥ 0 and x2 = y2, then x = y.
(iii) If (x + y)2 = x2 + y2 and y ≠ 0, then x = 0.
(iv) The diagonals of a parallelogram bisect each other.
Given that all women are mortal, and suppose that A is a woman, what can we conclude about A?
Answer
Since, all women are mortal and A is also a women.
∴ We can conclude that,
A is mortal.
Given that the product of two rational numbers is rational, and suppose a and b are rationals, what can you conclude about ab?
Answer
Since, product of two rational numbers is rational and a and b are rational.
∴ We can conclude that,
ab is rational.
Given that the decimal expansion of irrational numbers is non-terminating, non-recurring, and is irrational, what can we conclude about the decimal expansion of ?
Answer
Since, decimal expansion of irrational numbers is non-terminating, non-recurring, and is irrational.
∴ We can conclude that,
Decimal expansion of is non-terminating and non-recurring.
Given that y = x2 + 6 and x = -1, what can we conclude about the value of y?
Answer
Given,
x = -1
Substituting value of x in equation, y = x2 + 6, we get :
⇒ y = x2 + 6
⇒ y = (-1)2 + 6
⇒ y = 1 + 6 = 7.
Hence, y = 7.
Given that ABCD is a parallelogram and ∠B = 80°. What can you conclude about the other angles of the parallelogram?
Answer
We know that,
Opposite angles in a parallelogram are equal.
∴ ∠D = ∠B = 80°
Since, ∠A = ∠C = x (let)
We know that,
Sum of angles in a parallelogram is equal to 360°.
⇒ ∠A + ∠B + ∠C + ∠D = 360°
⇒ x + 80° + x + 80° = 360°
⇒ 2x + 160° = 360°
⇒ 2x = 200°
⇒ x = 100°
Hence, ∠A = ∠C = 100° and ∠D = 80°.
Given that PQRS is a cyclic quadrilateral and also its diagonals bisect each other. What can you conclude about the quadrilateral?
Answer
Let PQRS be a cyclic quadrilateral.
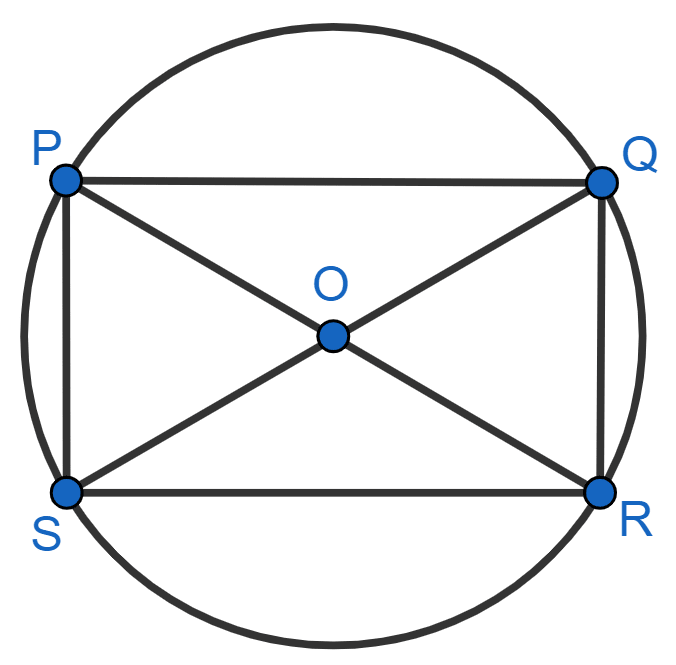
Given,
Diagonals bisect each other.
∴ PO = OR and SO = OQ.
From figure,
⇒ PO + OR = PR
⇒ PO + PO = PR
⇒ 2PO = PR
Since, PR is the diameter of the circle.
So, we can say that PO is the radius of the circle and OR is also the radius.
From figure,
⇒ SO + OQ = SQ
⇒ SO + SO = SQ
⇒ 2SO = SQ
Since, SQ is the diameter of the circle.
So, we can say that SO is the radius of the circle and OQ is also the radius.
∴ PO = OR = SO = OQ
∴ PO + OR = SO + OQ
∴ PR = SQ
Since, diagonals are equal.
Hence, we can conclude that PQRS is a rectangle.
Given that is irrational for all primes p and also suppose that 3721 is a prime. Can you conclude that is an irrational number? Is your conclusion correct? Why or why not?
Answer
Assuming 3721 to be a prime number.
Given,
is irrational for all primes p, hence is a prime number.
But,
= 61
61 is a rational number.
∴ The assumption that 3721 is a prime number is incorrect.
Hence, the conclusion is false.
Prove that the sum of two consecutive odd numbers is divisible by 4.
Answer
Let two consecutive odd numbers be (2n + 1) and (2n + 3) for some integer n.
Sum = (2n + 1) + (2n + 3)
= 4n + 4
= 4(n + 1).
On dividing the sum by 4, we get :
= n + 1.
Hence, proved that sum of two consecutive odd numbers is divisible by 4.
Take two consecutive odd numbers. Find the sum of their squares, and then add 6 to the result. Prove that the new number is always divisible by 8.
Answer
Let two consecutive odd numbers be (2n + 1) and (2n + 3) for some integer n.
Sum of squares = (2n + 1)2 + (2n + 3)2
= 4n2 + 1 + 4n + 4n2 + 9 + 12n
= 8n2 + 16n + 10
Adding 6 to the sum of squares we get
= 8n2 + 16n + 10 + 6
= 8n2 + 16n + 16
= 8(n2 + 2n + 2)
On dividing resultant sum by 8, we get :
= n2 + 2n + 2.
Hence, proved that the new number is divisible by 8.
If p ≥ 5 is a prime number, show that p2 + 2 is divisible by 3.
Answer
Given,
p ≥ 5
We know that,
Every prime number greater than 3 is of the form 6k + 1 or 6k + 5.
Let p be of form (6k + 1)
p2 + 2 = (6k + 1)2 + 2
= 36k2 + 1 + 12k + 2
= 36k2 + 3 + 12k
= 3(12k2 + 1 + 4k); which is clearly divisible by 3.
Let p be of the form (6k + 5)
p2 + 2 = (6k + 5)2 + 2
= 36k2 + 25 + 60k + 2
= 36k2 + 60k + 27
= 3(12k2 + 20k + 9); which is clearly divisible by 3.
Hence, proved that for p being prime number and p ≥ 5, p2 + 2 is divisible by 3.
Let x and y be rational numbers. Show that xy is a rational number.
Answer
Let x = , n ≠ 0 and y = , q ≠ 0, where m, n, p and q are integers. [By definition of rationals]
So,
Using properties of integers,
mp and nq are integers and since n, q are not equal to zero.
∴ nq ≠ 0.
∴ is a rational number.
Hence, proved that xy is also a rational number.
If a and b are positive integers, then you know that a = bq + r, 0 ≤ r < b, where q is a whole number. Prove that HCF (a, b) = HCF (b, r).
Answer
Given,
a, b are positive integer
a = bq + r and q is a whole number.
Let H.C.F. of a and b be c and let H.C.F. of b and r be d.
Since,
H.C.F. of a and b is c .......(1)
∴ a is divisible by c
∴ b is divisible by c or bq is divisible by c.
Given,
a = bq + r
r = a - bq
Since, c divides a and bq.
∴ a - bq is divisible by c.
∴ r is divisible by c.
∴ c is common divisor of b and r ....(2)
Since,
H.C.F. of b and r is d ........(3)
∴ r is divisible by d
∴ b is divisible by d or bq is divisible by d.
Since, d divides r and bq.
∴ r + bq is divisible by d.
∴ a is divisible by d.
∴ d is common divisor of a and b ....(4)
From statements (1), (2), (3) and (4), we get :
c = d
∴ H.C.F. (a, b) = H.C.F. (b, r).
Hence, proved that H.C.F. (a, b) = H.C.F. (b, r).
A line parallel to side BC of a triangle ABC, intersects AB and AC at D and E respectively. Prove that .
Answer
ΔABC with DE parallel to BC and intersecting AB and AC at D and E respectively is shown in the figure below:
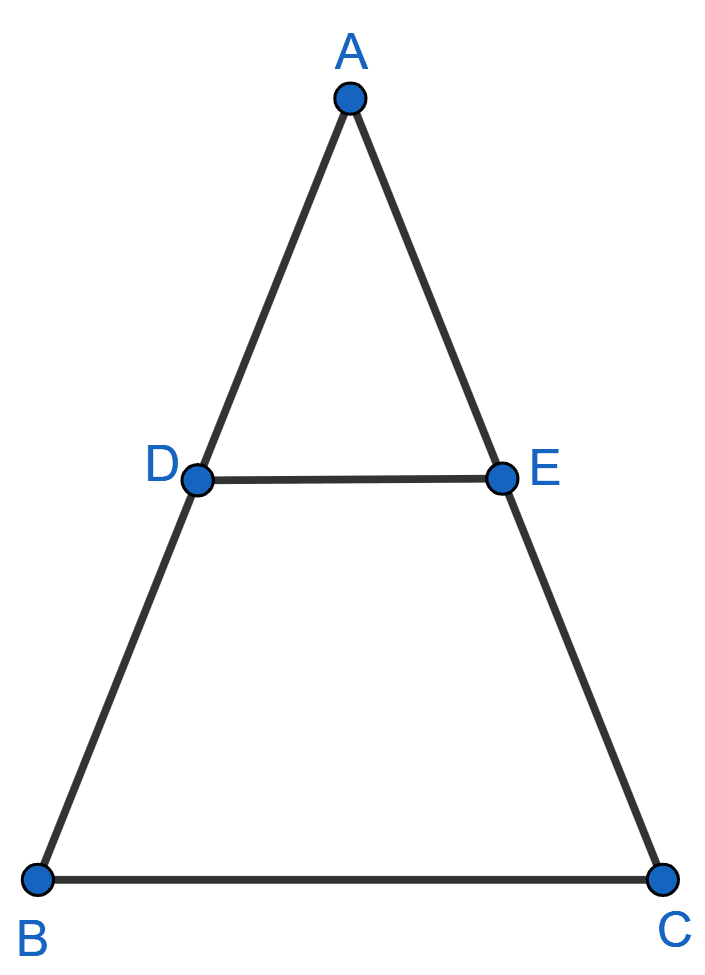
Join the vertex B of Δ ABC to E and the vertex C to D to form the lines BE and CD and then drop a perpendicular EN to the side AB and also draw DM ⊥ AC.
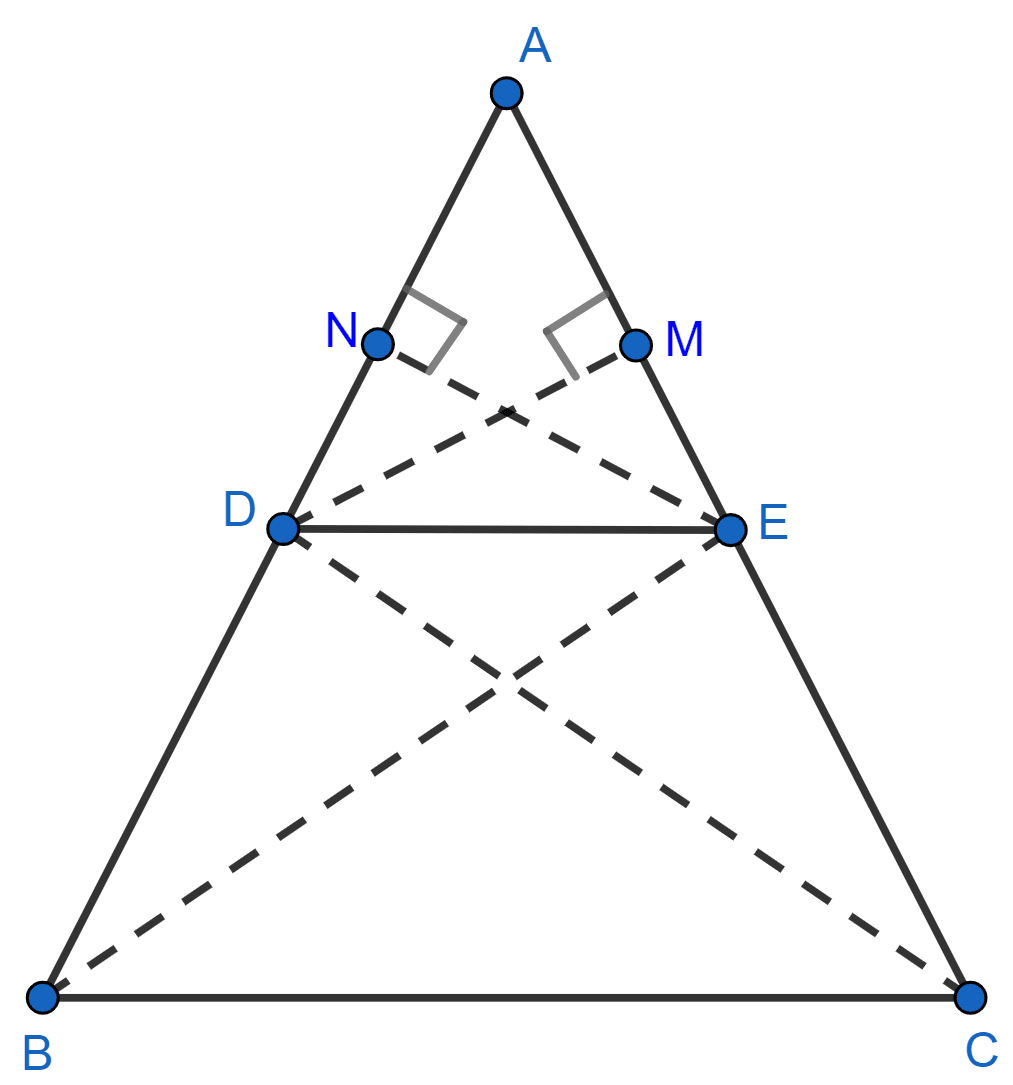
Area of Δ = Base × Height
Area of Δ ADE = ..........(1)
Area of Δ BDE = ..........(2)
Area of Δ ADE = ..........(3)
Area of Δ DEC = ...........(4)
Dividing equations (1) and (2), we get :
Dividing equations (3) and (4), we get :
From figure,
Δ BDE and Δ DEC are on the same base DE and between the same parallel lines BC and DE.
∴ Area of △ BDE = Area of △ DEC
..........[From (5) and (6)]
Hence, proved that .
State the negations for the following statements :
(i) Man is mortal.
(ii) Line l is parallel to line m.
(iii) This chapter has many exercises.
(iv) All integers are rational numbers.
(v) Some prime numbers are odd.
(vi) No student is lazy.
(vii) Some cats are not black.
(viii) There is no real number x, such that = -1.
(ix) 2 divides the positive integer a.
(x) Integers a and b are coprime.
Answer
(i) It is false that Man is mortal i.e., Man is not mortal.
(ii) It is false that line l is parallel to line m i.e., Line l is not parallel to line m.
(iii) It is false that this chapter has many exercises i.e., This chapter does not have many exercises.
(iv) It is false that all integers are rational numbers i.e., not all integers are rational numbers.
(v) It is false that some prime numbers are odd i.e., all prime numbers are not odd.
(vi) It is false that no student is lazy i.e., some students are lazy.
(vii) It is false that some cats are not black i.e., all cats are black.
(viii) It is false that there is no real number x, such that = -1 i.e., there is at least one real number x, such that = -1 .
(ix) It is false that 2 divides the positive integer a i.e., 2 does not divide the positive integer a.
(x) It is false that Integers a and b are coprime. i.e., Integers a and b are not coprime.
In each of the following questions, there are two statements. State if the second is the negation of the first or not.
(i) Mumtaz is hungry ; Mumtaz is not hungry.
(ii) Some cats are black ; Some cats are brown.
(iii) All elephants are huge ; One elephant is not huge.
(iv) All fire engines are red ; All fire engines are not red.
(v) No man is a cow ; Some men are cows.
Answer
| No. | Statement | Negation |
|---|---|---|
| (i) | Mumtaz is hungry | Mumtaz is not hungry |
| (ii) | Some cats are black | Some cats are not black |
| (iii) | All elephants are huge | All elephants are not huge |
| (iv) | All fire engines are red | Some fire engines are red |
| (v) | No man is a cow | Some men are cows |
(i) Yes (Since, the second statement matches with the negation.)
(ii) No (Since, the second statement does not matches with the negation.)
(iii) No (Since, the second statement does not matches with the negation.)
(iv) No (Since, the second statement does not matches with the negation.)
(v) Yes (Since, the second statement matches with the negation.)
Write the converses of the following statements.
(i) If it is hot in Tokyo, then Sharan sweats a lot.
(ii) If Shalini is hungry, then her stomach grumbles.
(iii) If Jaswant has a scholarship, then she can get a degree.
(iv) If a plant has flowers, then it is alive.
(v) If an animal is a cat, then it has a tail.
Answer
(i) If Sharan sweats a lot, then it is hot in Tokyo.
(ii) If Shalini’s stomach grumbles, then she is hungry.
(iii) If Jaswant can get a degree, then she has a scholarship.
(iv) If a plant is alive, then it has flowers.
(v) If an animal has a tail, then it is a cat.
Write the converses of the following statements. Also, decide in each case whether the converse is true or false.
(i) If triangle ABC is isosceles, then its base angles are equal.
(ii) If an integer is odd, then its square is an odd integer.
(iii) If x2 = 1, then x = 1.
(iv) If ABCD is a parallelogram, then AC and BD bisect each other.
(v) If a, b and c, are whole numbers, then a + (b + c) = (a + b) + c.
(vi) If x and y are two odd numbers, then x + y is an even number.
(vii) If vertices of a parallelogram lie on a circle, then it is a rectangle.
Answer
(i) If the base angles of triangle ABC are equal, then it is isosceles. This is a true statement.
(ii) If the square of an integer is odd, then the integer is odd. This is a true statement.
(iii) If x = 1, then x2 = 1. This is a true statement.
(iv) If AC and BD bisect each other, then ABCD is a parallelogram. This is a true statement.
(v) If a + (b + c) = (a + b) + c, then a, b and c are whole numbers. This is a false statement.
(vi) If x + y is an even number, then x and y are odd. This is a false statement.
(vii) If a parallelogram is a rectangle, its vertices lie on a circle. This is a true statement.
Suppose a + b = c + d, and a < c. Use proof by contradiction to show b > d.
Answer
Suppose b ≤ d,
Given,
⇒ a + b = c + d
⇒ c - a = b - d ...........(1)
Since, a < c so, c - a will be positive.
According to equation (1),
b - d = c - a
∴ b - d will also be positive.
It is not possible as we have assumed b ≤ d.
So, our assumption is wrong.
Hence, proved that b > d.
Let r be a rational number and x be an irrational number. Use proof by contradiction to show that r + x is an irrational number.
Answer
By seeking contradiction,
Let r + x is a rational number.
We know that,
Rational number can be expressed in the form of , where p, q ∈ I and q ≠ 0.
So,
From above we see,
That x is a rational number.
This is not possible as in question it is given that x is an irrational number.
Our assumption of r + x being a rational number is wrong.
Hence, proved that r + x is an irrational number.
Use proof by contradiction to prove that if for an integer a, a2 is even, then so is a.
Answer
By seeking contradiction,
Let a2 be even and a be odd.
So, a will be of form,
a = (2n + 1) for any integer n.
⇒ a2 = (2n + 1)2
⇒ a2 = 4n2 + 4n + 1
⇒ a2 = 4(n2 + n) + 1
Let (n2 + n) = k
⇒ a2 = 4k + 1
For any integer k, on multiplying by 4 makes it even and adding 1 to an even no. makes it odd.
So, a2 will be an odd number, which is not possible.
So, our assumption is wrong i.e. a is not odd.
Hence, proved that for an integer a if a2 is even, then so is a.
Use proof by contradiction to prove that if for an integer a, a2 is divisible by 3, then a is divisible by 3.
Answer
By seeking contradiction,
Let a2 is divisible by 3 and a is not divisible by 3.
So, a can be of the form :
⇒ a = 3k + 1 and a = 3k + 2
⇒ a2 = (3k + 1)2 or a2 = (3k + 2)2
⇒ a2 = 9k2 + 6k + 1 or a2 = 9k2 + 12k + 4
⇒ a2 = 3(3k2 + 2k) + 1 or a2 = 3(3k2 + 4k) + 4
Let 3k2 + 2k = c and 3k2 + 4k = d.
a2 = 3c + 1 or a2 = 3d + 4
We know for any integer c and d 3c + 1 and 3d + 4 is not divisible by 3.
So, a2 will not be divisible by 3.
So, our assumption is wrong
∴ a will be divisible by 3.
Hence, proved that if for an integer a, a2 is divisible by 3, then a is divisible by 3.
Use proof by contradiction to show that there is no value of n for which 6n ends with the digit zero.
Answer
By seeking contradiction,
Let 6n ends with 0.
6n = (2 × 3)n
= 2n × 3n
No value of 2n × 3n can end with zero.
Hence, our assumption is wrong.
Hence, proved that for no value of n, 6n ends with the digit zero.
Prove by contradiction that two distinct lines in a plane cannot intersect in more than one point.
Answer
Suppose two distinct lines l and m intersect at a point P.
Let us suppose they will intersect at another point, say Q (different from P).
It means two lines l and m passing through two distinct point P and Q.
We know that,
Given two distinct points, there exists one and only one line passing through them.
So our assumption is wrong.
Hence, proved that two distinct lines cannot have more than one point in common.