Circles

How many tangents can a circle have?

Answer

A circle can have infinitely many tangents.

Fill in the blanks :

(i) A tangent to a circle intersects it in ............... point (s).

(ii) A line intersecting a circle in two points is called a ...............

(iii) A circle can have ............... parallel tangents at the most.

(iv) The common point of a tangent to a circle and the circle is called ...............

Answer

(i) One

(ii) Secant

(iii) Two

(iv) Point of contact

A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is :

1. 12 cm

2. 13 cm

3. 8.5 cm

4. $\sqrt{119}$ cm.

Answer

We know that,

The tangent at any point of a circle is perpendicular to the radius through the point of contact.

From figure,

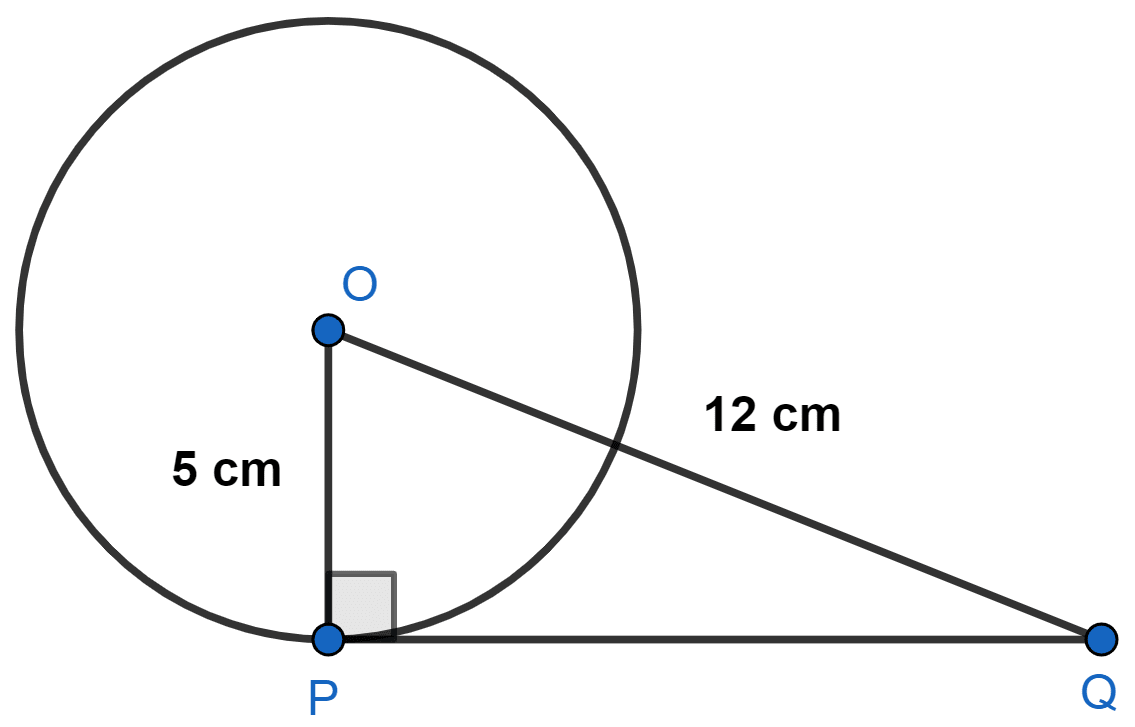
PQ is the tangent.

So,

OP ⊥ PQ

In △OPQ,

By pythagoras theorem,

⇒ OQ² = OP² + PQ²

⇒ 12² = 5² + PQ²

⇒ 144 = 25 + PQ²

⇒ PQ² = 144 - 25

⇒ PQ² = 119

⇒ PQ = $\sqrt{119}$ cm.

Hence, Option 4 is the correct option.

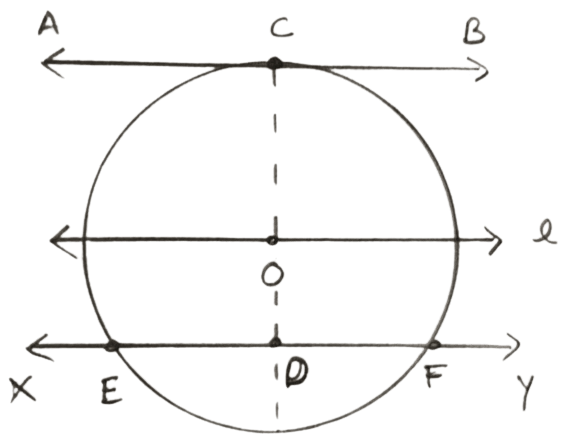
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.

Answer

Steps of construction :

1. Draw a line l and mark a point O on it. With O as center draw a circle of any convenient radius.

2. Mark a point C on the circumference of the circle such that O, C lie in the same imaginary line.

3. Draw a line AB parallel to line l passing through point C. AB is the required tangent.

4. Mark a point D inside the circle such that the points C, O, D are on the same imaginary line.

5. Draw XY, a line parallel to l touching the circle at point E and F. EF is the required secant.

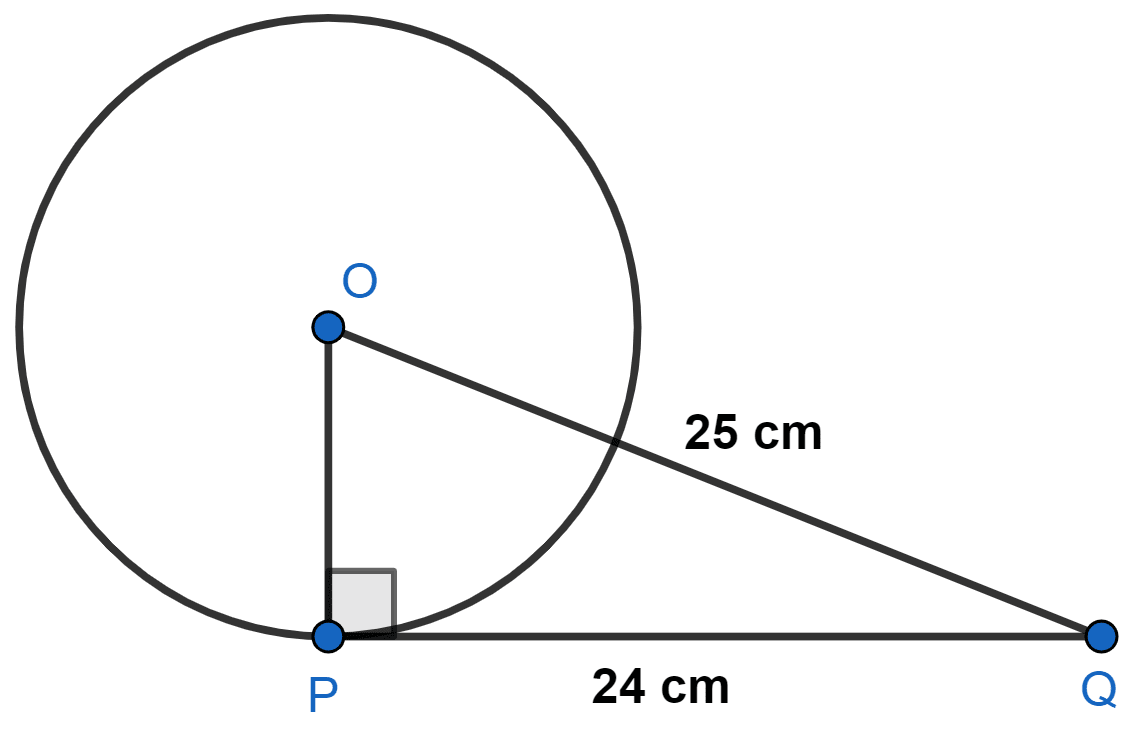
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is

1. 7 cm

2. 12 cm

3. 15 cm

4. 24.5 cm

Answer

Let P be the point of contact of tangent with the circle and O be the center of the circle.

We know that,

The tangent at any point of a circle is perpendicular to the radius through the point of contact.

So,

OP ⊥ PQ

In △OPQ,

By pythagoras theorem,

⇒ OQ² = OP² + PQ²

⇒ 25² = OP² + 24²

⇒ 625 = OP² + 576

⇒ OP² = 625 - 576

⇒ OP² = 49

⇒ OP = $\sqrt{49}$ = 7 cm.

Hence, Option 1 is the correct option.

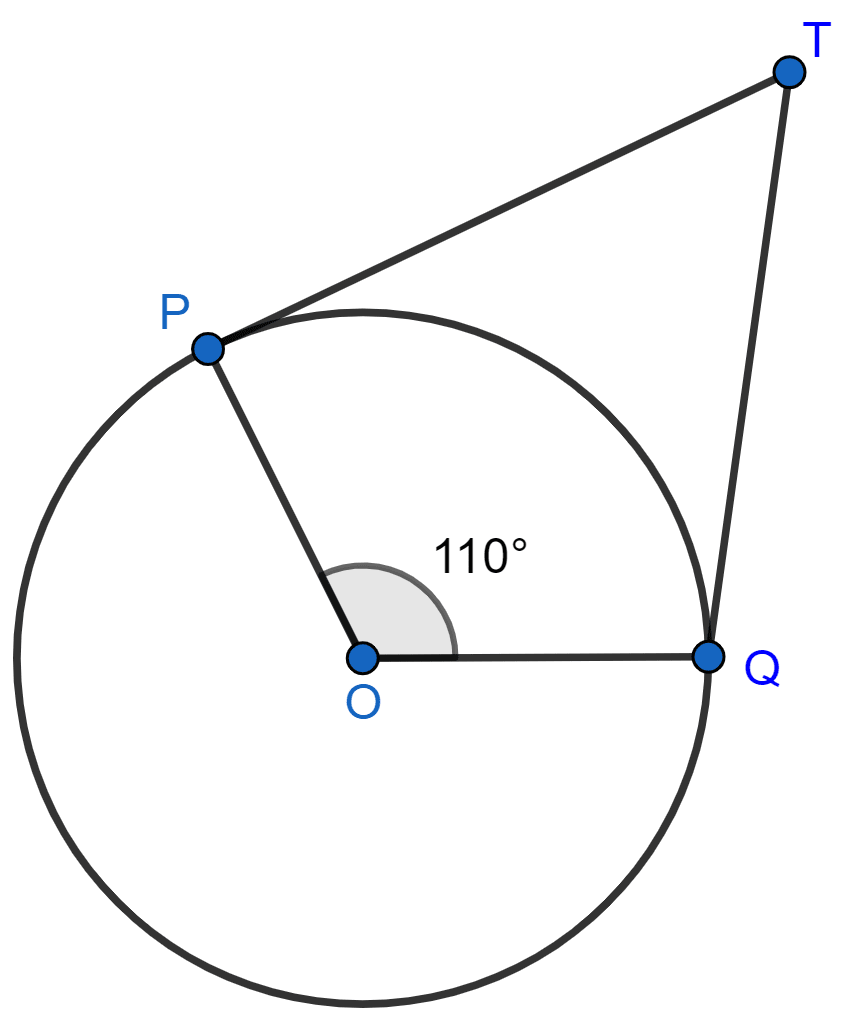
In the given figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to

1. 60°

2. 70°

3. 80°

4. 90°

Answer

We know that,

The tangent at any point of a circle is perpendicular to the radius through the point of contact.

So,

OP ⊥ PT and OQ ⊥ QT

∠OPT = 90° and ∠OQT = 90°

In quadrilateral OPTQ,

⇒ ∠OPT + ∠PTQ + ∠OQT + ∠POQ = 360°

⇒ 90° + ∠PTQ + 90° + 110° = 360°

⇒ ∠PTQ + 290° = 360°

⇒ ∠PTQ = 360° - 290° = 70°.

Hence, Option 2 is the correct option.

If tangents PA and PB from a point P to a circle with center O are inclined to each other at angle of 80°, then ∠POA is equal to

1. 50°

2. 60°

3. 70°

4. 80°

Answer

We know that,

The lengths of tangents drawn from an external point to a circle are equal.

A tangent at any point of a circle is perpendicular to the radius at the point of contact.

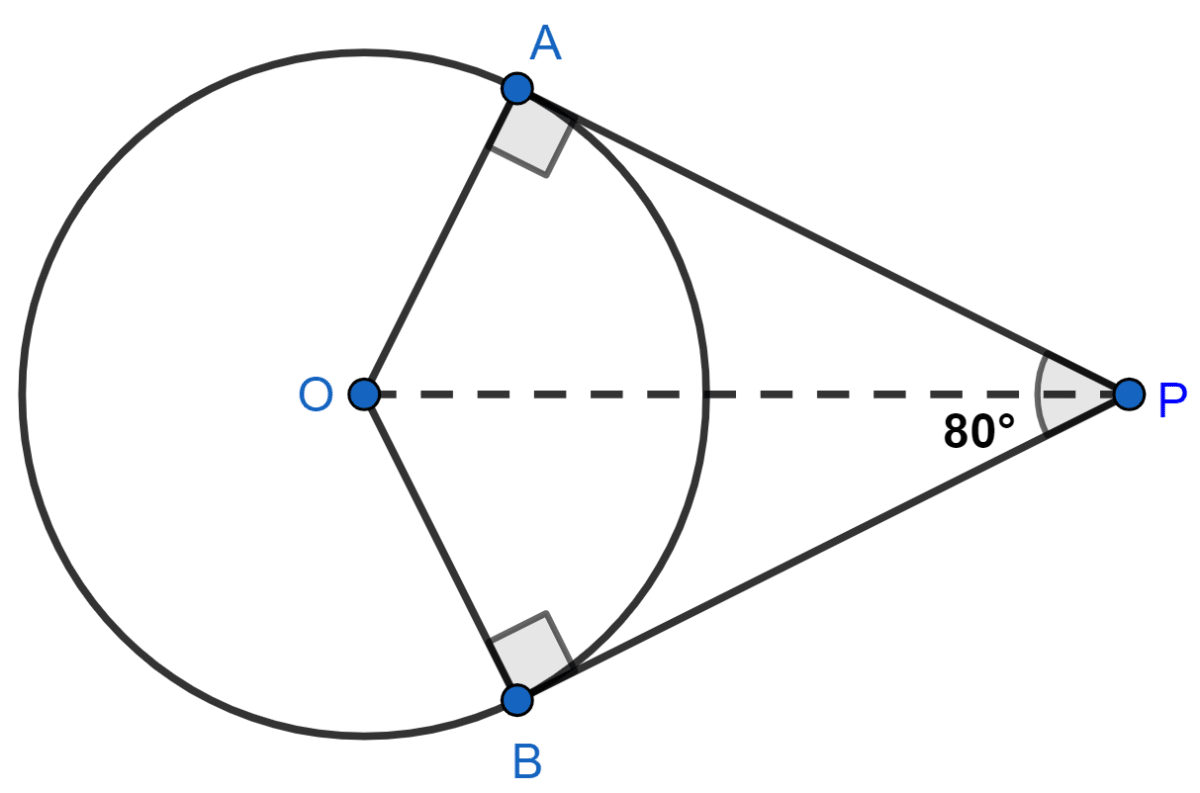
In Δ OAP and Δ OBP,

⇒ OA = OB (radii of the circle are always equal)

⇒ AP = BP (length of the tangents)

⇒ OP = OP (common)

Therefore, by SSS congruency Δ OAP ≅ Δ OBP

Also,

By C.P.C.T.,

⇒ ∠POA = ∠POB

⇒ ∠OPA = ∠OPB

Therefore, OP is the angle bisector of ∠APB and ∠AOB.

Hence, ∠OPA = ∠OPB = $\dfrac{1}{2} \times$ ∠APB

= $\dfrac{1}{2}$ × 80°

= 40°.

In Δ OAP

We know that,

OA ⊥ AP ( The tangent at any point of a circle is perpendicular to the radius through the point of contact.)

∴ ∠OAP = 90°.

By angle sum property of a triangle,

⇒ ∠OAP + ∠POA + ∠OPA = 180°

⇒ 90° + ∠POA + 40° = 180°

⇒ 130° + ∠POA = 180°

⇒ ∠POA = 180° - 130°

⇒ ∠POA = 50°.

Hence, Option 1 is the correct option.

Prove that the tangents drawn at the ends of a diameter of a circle are parallel.

Answer

Let PQ and RS be tangents to the circle at the ends of the diameter AB.

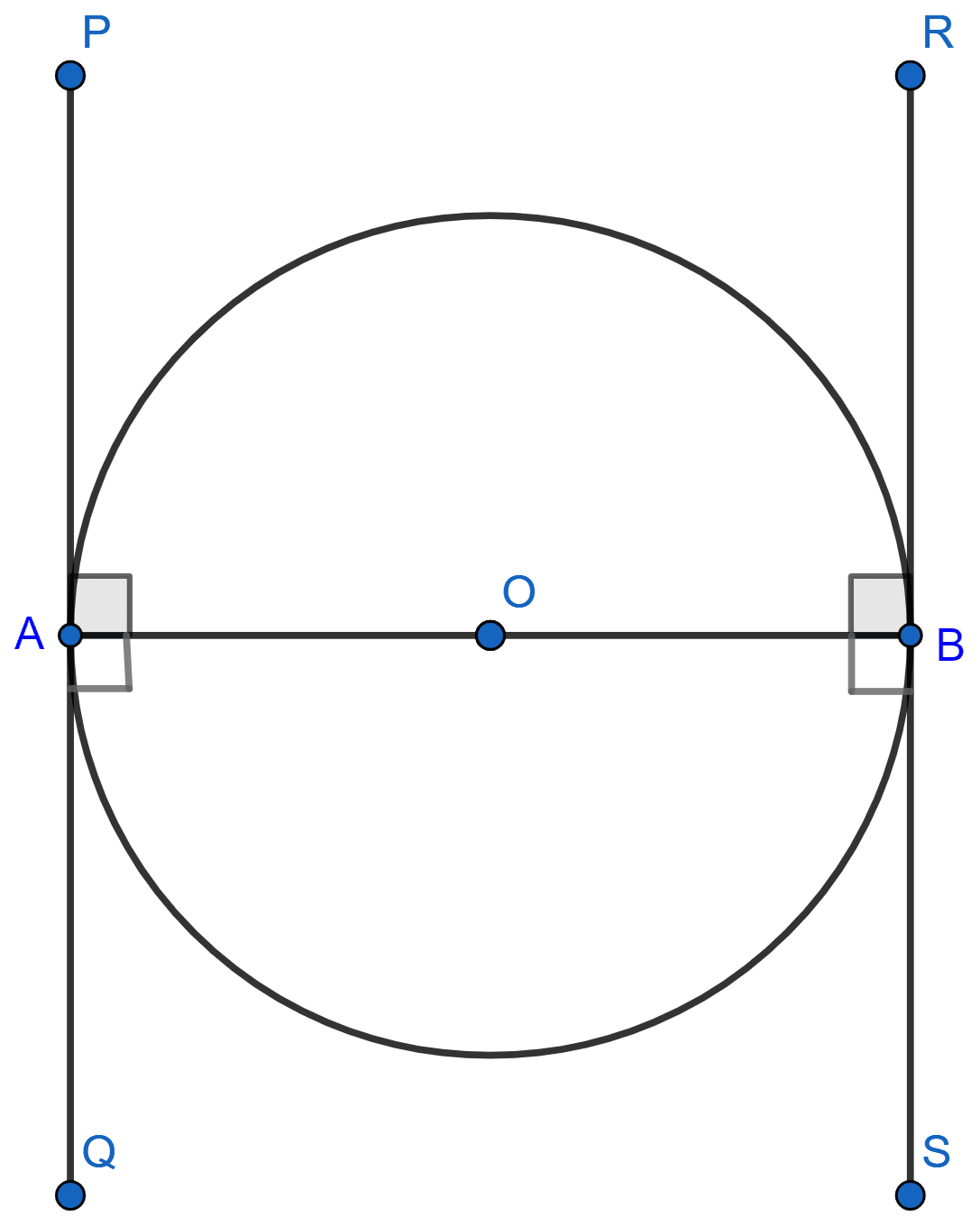
We know that,

The tangent at any point of a circle is perpendicular to the radius through the point of contact.

Thus, OA ⊥ PQ and OB ⊥ RS

∴ ∠PAO = 90°, ∠RBO = 90°, ∠OAQ = 90° and ∠OBS = 90°

Here, ∠OAQ is equal to ∠OBR and ∠PAO is equal to ∠OBS, which are two pairs of alternate interior angles.

If the alternate interior angles are equal, then lines PQ and RS should be parallel.

Hence, proved that tangents drawn at the ends of a diameter of a circle are parallel.

Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.

Answer

Let PQ be tangent to circle with center O.

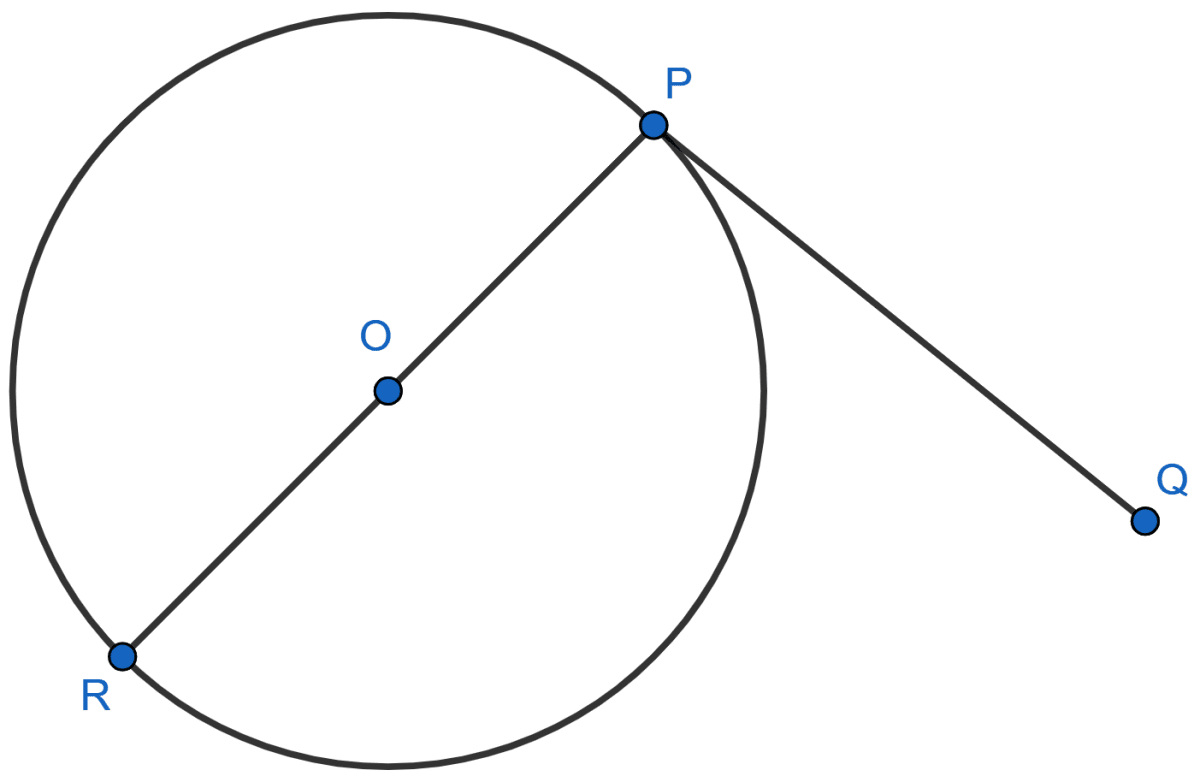
We know that,

Tangent at any point of a circle is perpendicular to the radius through the point of contact.

At the point of contact P, RP is perpendicular to the tangent PQ.

We know that,

Radius or diameter will always pass through the centre of the circle.

∴ PR passes through the centre O.

Hence it is proved that perpendicular PR of tangent PQ passes through centre O.

The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.

Answer

Let P be the point of contact of tangent to the circle with center O.

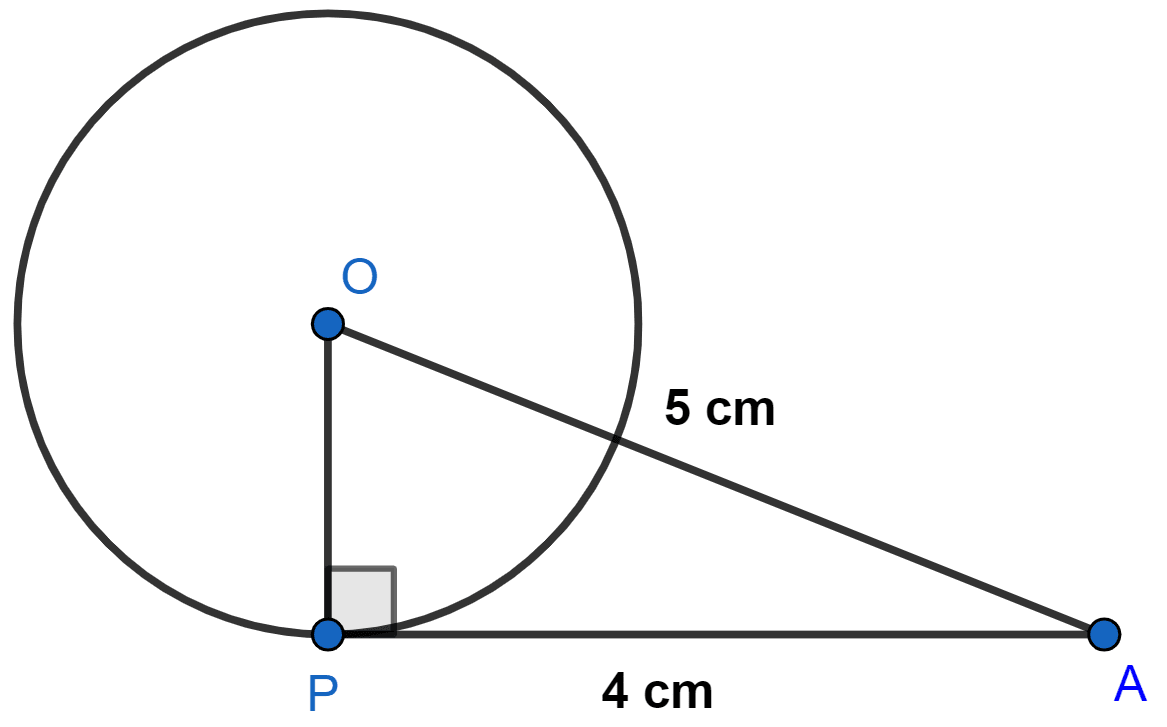
We know that,

Tangent at any point of a circle is perpendicular to the radius through the point of contact.

In right angle triangle OPA,

By pythagoras theorem,

⇒ OA² = OP² + AP²

⇒ 5² = OP² + 4²

⇒ OP² = 25 - 16

⇒ OP² = 9

⇒ OP = $\sqrt{9}$ = 3 cm.

Hence, radius of circle = 3 cm.

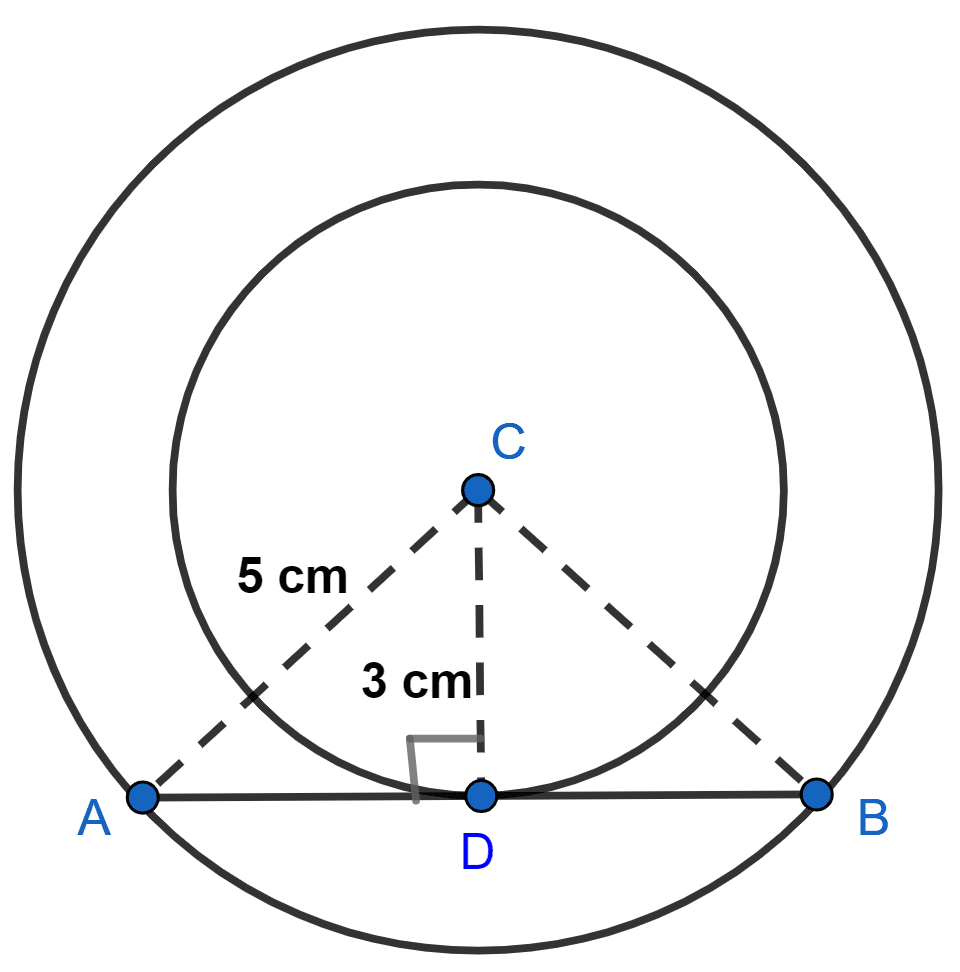
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.

Answer

Let C be the center of concentric circles and AB be the chord of larger circle touching smaller circle at point D.

So, AB can be the tangent to smaller circle.

We know that,

The tangent at any point of a circle is perpendicular to the radius through the point of contact.

∴ CD ⊥ AB.

In right angle triangle ACD,

By pythagoras theorem,

⇒ AC² = AD² + CD²

⇒ 5² = AD² + 3²

⇒ AD² = 25 - 9

⇒ AD² = 16

⇒ AD = $\sqrt{16}$ = 4 cm.

In △DAC and △DBC,

⇒ ∠CDA = ∠CDB (Both equal to 90°)

⇒ AC = BC = 5 cm

⇒ CD = CD (Common)

∴ △DAC ≅ △DBC (By SAS axiom)

∴ AD = BD (By C.P.C.T.)

∴ BD = 4 cm.

AB = AD + BD = 4 + 4 = 8 cm.

Hence, length of required chord = 8 cm.

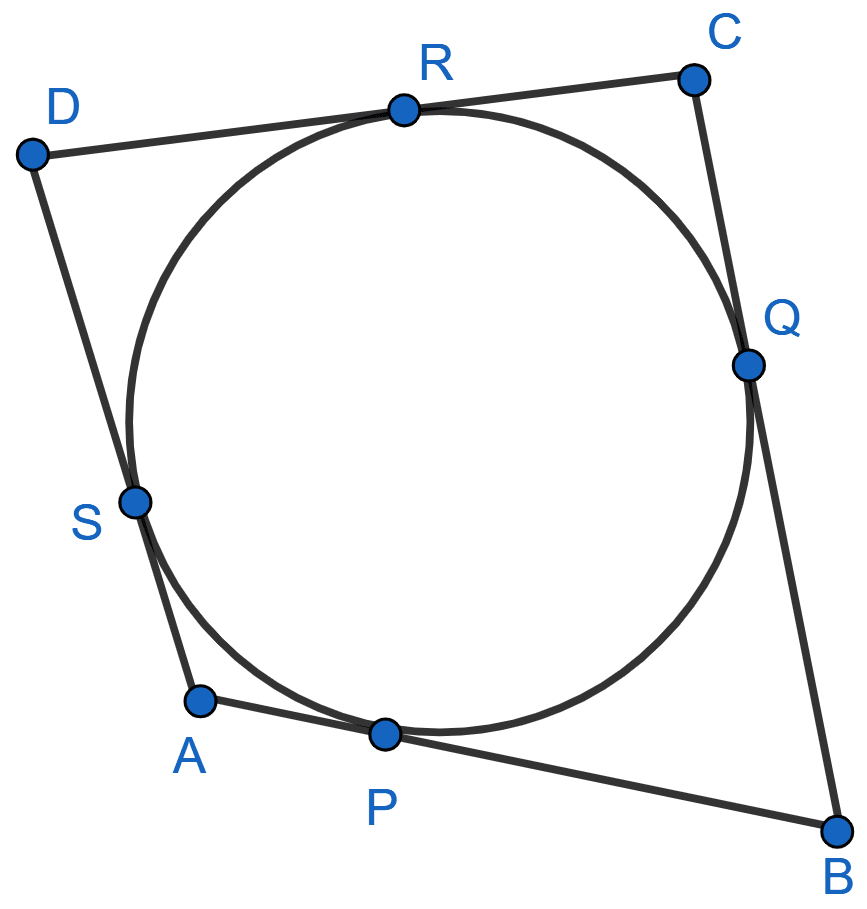
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that :

AB + CD = AD + BC

Answer

We know that,

Tangents drawn from a point to a circle are equal in length.

Therefore,

AS = AP = p (let)

BP = BQ = q (let)

CR = CQ = r (let)

DR = DS = s (let)

To prove :

AB + CD = AD + BC

Solving L.H.S. of above equation :

⇒ AB + CD

⇒ (AP + PB) + (CR + DR)

⇒ p + q + r + s.

Solving L.H.S. of above equation :

⇒ AD + BC

⇒ (AS + DS) + (BQ + CQ)

⇒ (p + s) + (q + r)

⇒ p + q + r + s.

Since, L.H.S. = R.H.S.

Hence, proved that AB + CD = AD + BC.

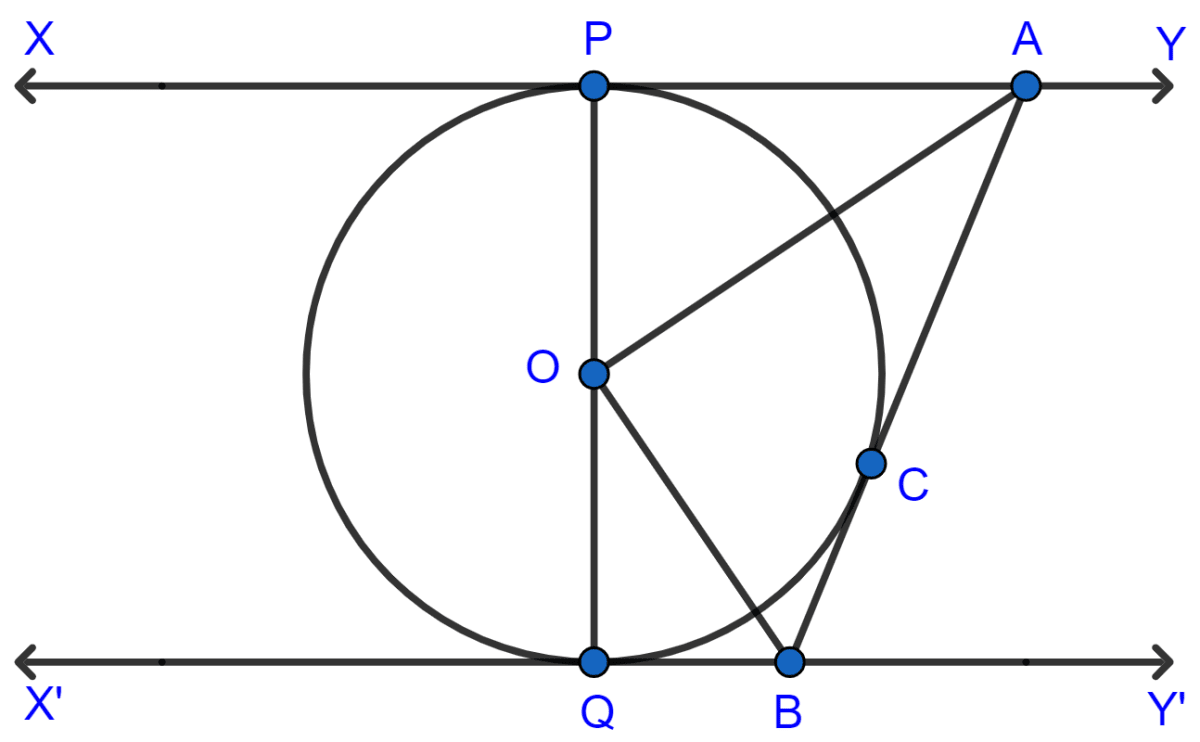
In the given figure, XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X'Y' at B. Prove that ∠AOB = 90°.

Answer

Draw a line between points O and C.

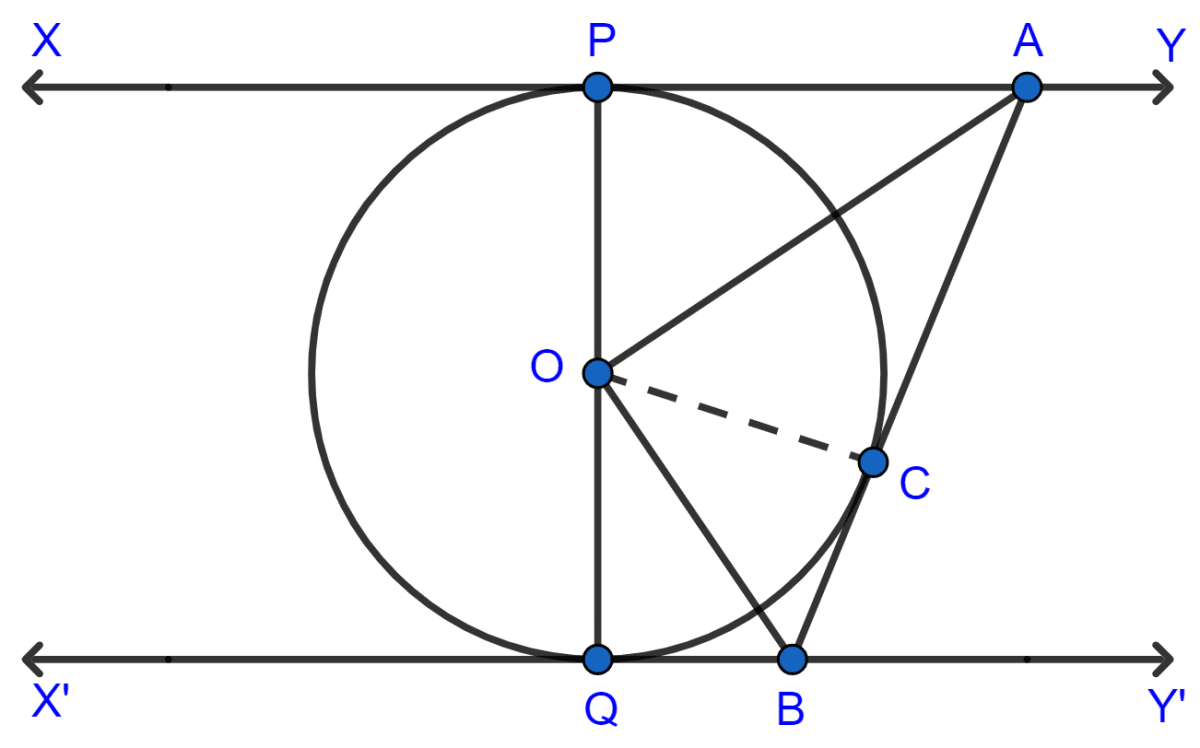
In Δ OPA and Δ OCA,

⇒ OP = OC (Radii of the circle)

⇒ AP = AC (The lengths of tangents drawn from an external point to a circle are always equal.)

⇒ AO = AO (Common)

∴ Δ OPA ≅ Δ OCA (By SSS axiom)

By C.P.C.T.,

∠POA = ∠AOC ........... (1)

In Δ COB and Δ BOQ,

⇒ OQ = OC (Radii of the circle)

⇒ BC = BQ (The lengths of tangents drawn from an external point to a circle are always equal.)

⇒ OB = OB (Common)

∴ Δ COB ≅ Δ BOQ (By SSS axiom)

By C.P.C.T.

∴ ∠COB = ∠BOQ ........... (2)

PQ is a diameter, hence a straight line and ∠POQ = 180°

From figure,

⇒ ∠POQ = ∠POA + ∠AOC + ∠COB + ∠BOQ

⇒ ∠POA + ∠AOC + ∠COB + ∠BOQ = 180°

⇒ ∠AOC + ∠AOC + ∠COB + ∠COB = 180° [From equation (1) and (2)]

⇒ 2∠AOC + 2∠COB = 180°

⇒ 2(∠AOC + ∠COB) = 180°

⇒ ∠AOC + ∠COB = 90°

From the figure,

⇒∠AOC + ∠COB = ∠AOB

∴ ∠AOB = 90°

Hence proved that ∠AOB = 90°.

Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.

Answer

Let us consider O as the centre point of the circle. Let P be a point outside the circle from which two tangents PA and PB are drawn to the circle which touches the circle at point A and B respectively.

Draw a line segment between points A and B such that it subtends ∠AOB at centre O of the circle.

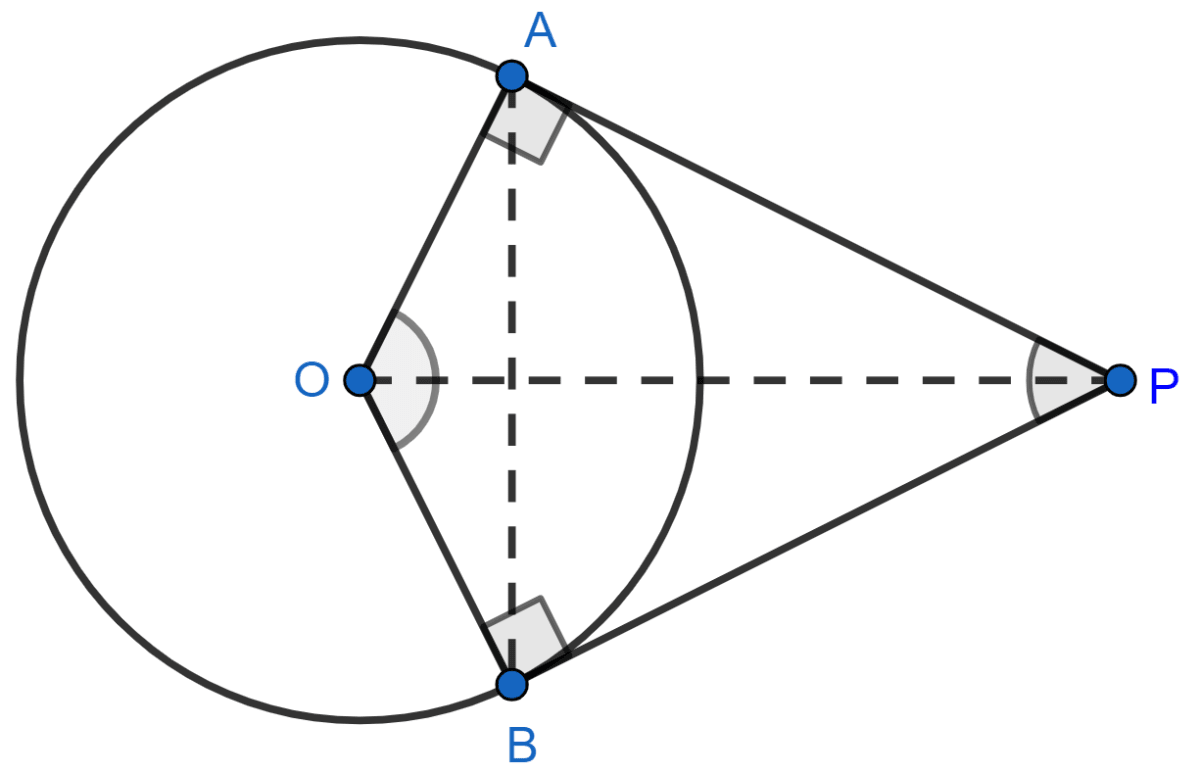
We know that,

The tangent at any point of a circle is always perpendicular to the radius through the point of contact.

∴ ∠OAP = ∠OBP = 90° ............(1)

In a quadrilateral, the sum of interior angles is 360°.

In quadrilateral OAPB,

⇒ ∠OAP + ∠APB + ∠PBO + ∠BOA = 360°

Using Equation (1), we can write the above equation as

⇒ 90° + ∠APB + 90° + ∠BOA = 360°

⇒ ∠APB + ∠BOA = 360° - 180°

⇒ ∠APB + ∠BOA = 180°

Where,

∠APB = Angle between the two tangents PA and PB from external point P.

∠BOA = Angle subtended by the line segment AB joining the point of contacts at the centre.

Hence, proved the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.

Prove that the parallelogram circumscribing a circle is a rhombus.

Answer

ABCD is a parallelogram. Therefore, opposite sides are parallel and equal.

∴ AB || CD and BC || AD.

∴ AB = CD and BC = AD

The lengths of tangents drawn from an external point to a circle are equal.

Therefore,

⇒ BP = BQ ........... (1)

⇒ CR = CQ ........... (2)

⇒ DR = DS ........... (3)

⇒ AP = AS ........... (4)

Adding (1) + (2) + (3) + (4), we get :

⇒ BP + CR + DR + AP = BQ + CQ + DS + AS

⇒ (BP + AP) + (CR + DR) = (BQ + CQ) + (DS + AS)

⇒ AB + CD = BC + AD

Substitute CD = AB and AD = BC since ABCD is a parallelogram, then

⇒ AB + AB = BC + BC

⇒ 2AB = 2BC

⇒ AB = BC

∴ AB = BC = CD = DA

This implies that all the four sides are equal.

Hence, proved that the parallelogram circumscribing a circle is a rhombus.

A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively in figure. Find the sides AB and AC.

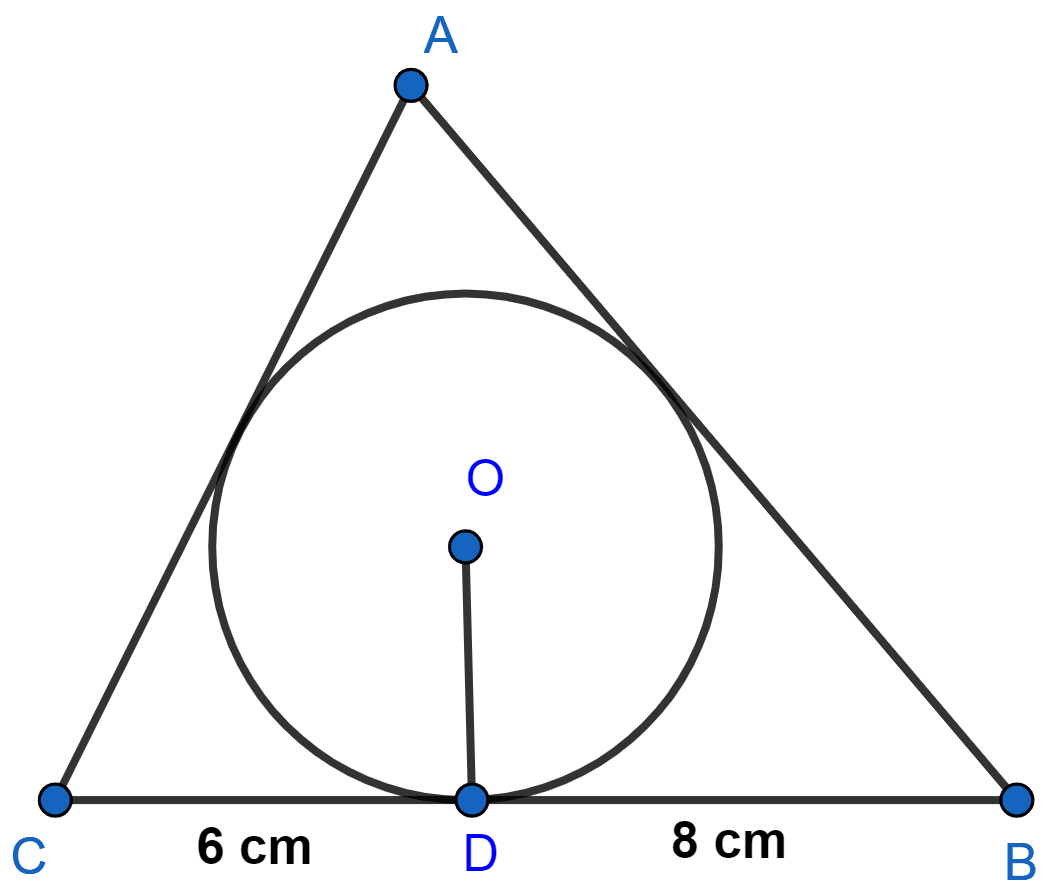
Answer

Draw OE perpendicular to AC and OF perpendicular to AB.

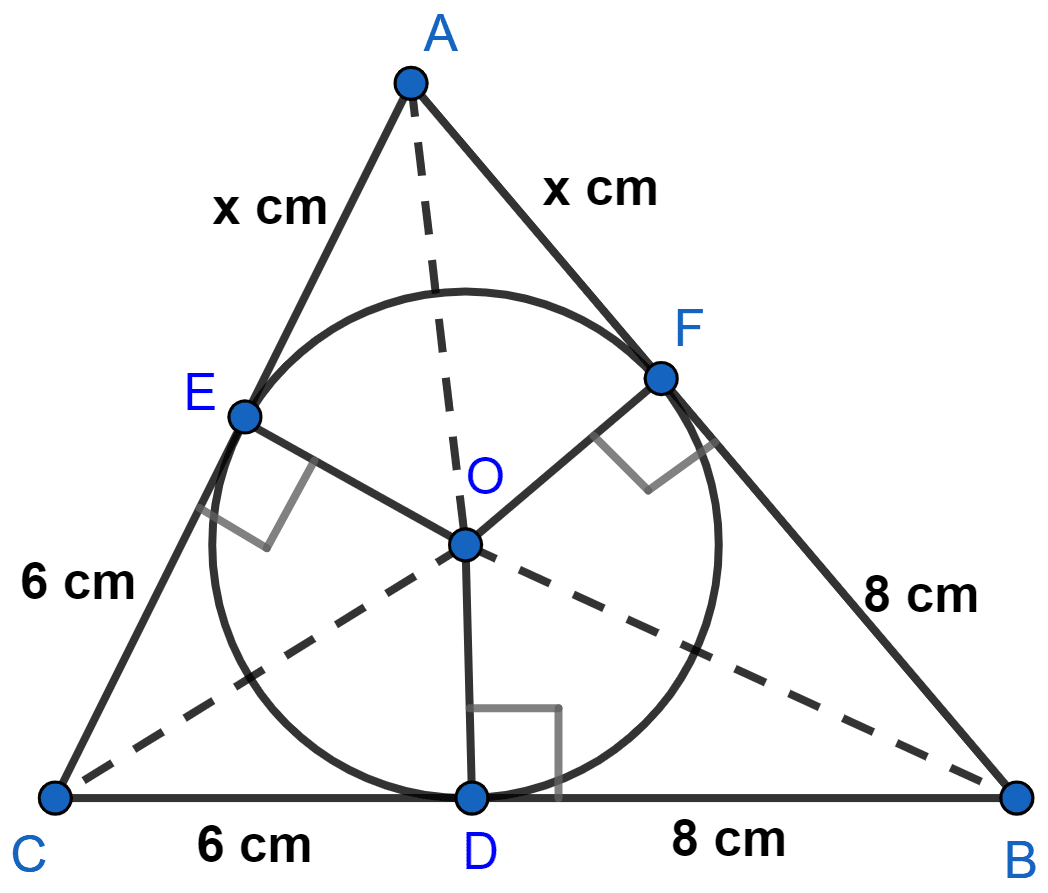
We know that,

The lengths of tangents drawn from an external point to a circle are equal.

CE = CD = 6 cm, BF = BD = 8 cm.

AE = AF = x cm (let)

By heron's formula,

Area = $\sqrt{s(s - a)(s - b)(s - c)}$, where a, b and c are sides of triangle and s = $\dfrac{1}{2}$ (AB + BC + AC).

Substituting values we get :

$s = \dfrac{1}{2}[(AF + BF) + (BD + CD) + (AE + CE)] \\[1em] = \dfrac{1}{2}[(x + 8) + (8 + 6) + (x + 6)] \\[1em] = \dfrac{1}{2}[2x + 28] \\[1em] = \dfrac{1}{2} \times 2[x + 14] \\[1em] = x + 14.$

Substituting value of s in Heron's formula,

$\text{Area } = \sqrt{(x + 14)(x + 14 - AB)(x + 14 - BC)(x + 14 - AC)} \\[1em] = \sqrt{(x + 14)[x + 14 - (x + 8)][x + 14 - 14][x + 14 - (x + 6)]} \\[1em] = \sqrt{(x + 14)\times 6 \times x \times 8} \\[1em] = \sqrt{48(x^2 + 14x)} \text{ cm}^2.$

From figure,

Area of △ABC = Area of △AOB + Area of △BOC + Area of △AOC ............(1)

We know that,

Area of triangle = $\dfrac{1}{2} \times \text{ base } \times \text{height}$

Substituting values we get :

$\text{Area of △AOB } = \dfrac{1}{2} \times AB \times OF \\[1em] = \dfrac{1}{2} \times (x + 8) \times 4 \\[1em] = 2(x + 8) \\[1em] = (2x + 16) \text{ cm}^2. \\[1em] \text{Area of △BOC } = \dfrac{1}{2} \times BC \times OD \\[1em] = \dfrac{1}{2} \times 14 \times 4 \\[1em] = 28 \text{ cm}^2. \\[1em] \text{Area of △AOC } = \dfrac{1}{2} \times AC \times OE \\[1em] = \dfrac{1}{2} \times (x + 6) \times 4 \\[1em] = 2(x + 6) \\[1em] = (2x + 12) \text{ cm}^2. \\[1em]$

Substituting values in equation (1), we get :

$\Rightarrow \sqrt{48(x^2 + 14x)} = (2x + 16) + 28 + (2x + 12) \\[1em] \Rightarrow \sqrt{48(x^2 + 14x)} = 4x + 56 \\[1em] \Rightarrow \sqrt{48(x^2 + 14x)} = 4(x + 14)$

Squaring both sides we get :

$\Rightarrow 48(x^2 + 14x) = 4^2 \times (x + 14)^2 \\[1em] \Rightarrow 48(x^2 + 14x) = 16(x^2 + 196 + 28x) \\[1em] \Rightarrow \dfrac{48}{16}(x^2 + 14x) = x^2 + 196 + 28x \\[1em] \Rightarrow 3x^2 + 42x = x^2 + 196 + 28x \\[1em] \Rightarrow 3x^2 - x^2 + 42x - 28x - 196 = 0 \\[1em] \Rightarrow 2x^2 + 14x - 196 = 0 \\[1em] \Rightarrow 2(x^2 + 7x - 98) = 0 \\[1em] \Rightarrow x^2 + 7x - 98 = 0 \\[1em] \Rightarrow x^2 + 14x - 7x - 98 = 0 \\[1em] \Rightarrow x(x + 14) - 7(x + 14) = 0 \\[1em] \Rightarrow (x - 7)(x + 14) = 0 \\[1em] \Rightarrow x - 7 = 0 \text{ or } x + 14 = 0 \\[1em] \Rightarrow x = 7 \text{ or } x = -14.$

Since, side cannot be negative.

∴ x = 7 cm.

From figure,

AB = AF + BF = x + 8 = 7 + 8 = 15 cm

AC = AE + CE = x + 6 = 7 + 6 = 13 cm.

Hence, AB = 15 cm and AC = 13 cm.

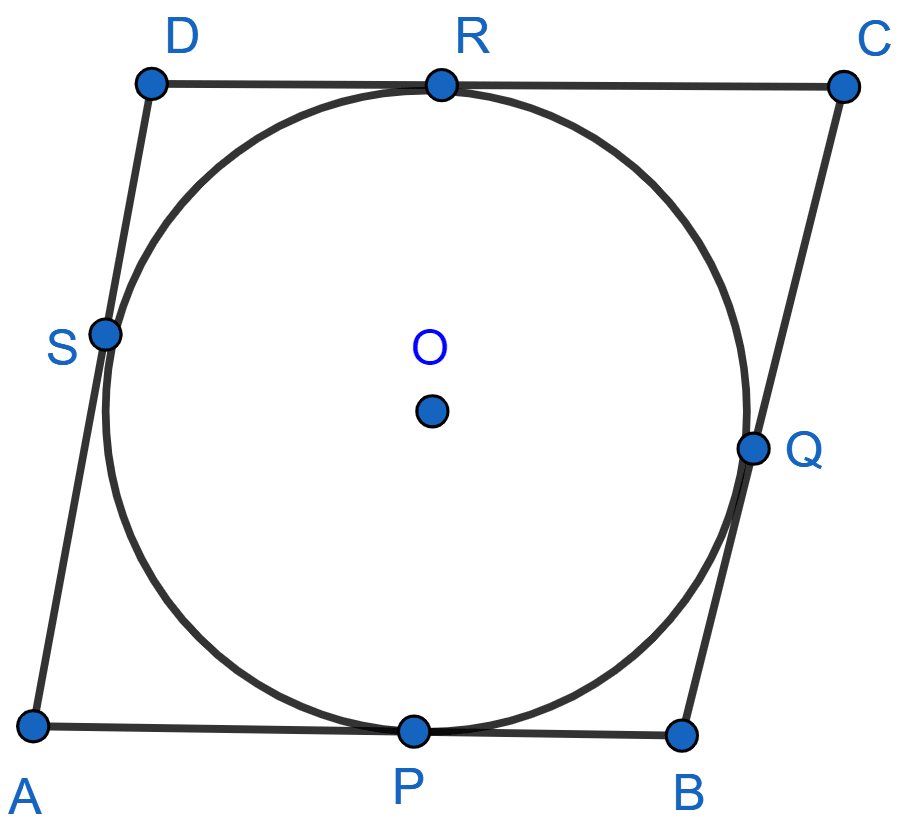
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.

Answer

In the below figure, P, Q, R, S are points of contact

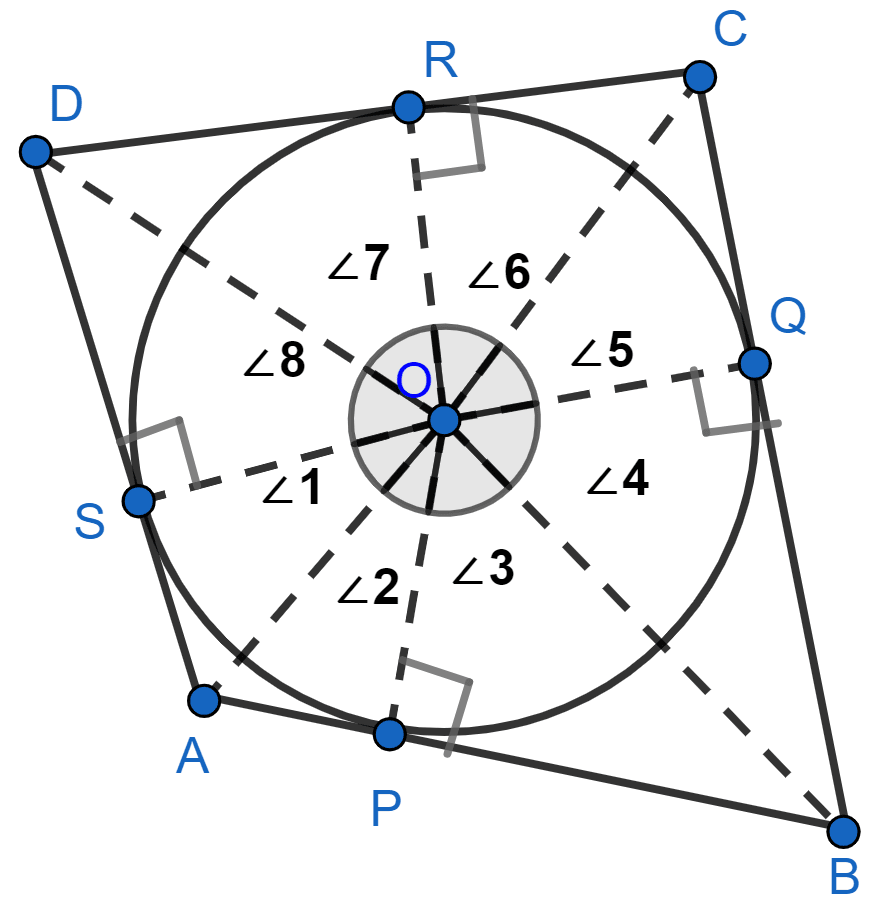
We know that,

The tangents drawn from an external point to a circle are equal.

AS = AP

We know that,

Tangents drawn from a point outside the circle, subtend equal angles at the centre.

∠1 = ∠2, ∠3 = ∠4, ∠5 = ∠6, ∠7 = ∠8.

Since complete angle is 360° at the centre,

We have,

⇒ ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°

⇒ ∠1 + ∠1 + ∠4 + ∠4 + ∠5 + ∠5 + ∠8 + ∠8 = 360° or ∠2 + ∠2 + ∠3 + ∠3 + ∠6 + ∠6 + ∠7 + ∠7 = 360°

⇒ 2(∠1 + ∠8 + ∠4 + ∠5) = 360° or 2 (∠2 + ∠3 + ∠6 + ∠7) = 360°

⇒ ∠1 + ∠8 + ∠4 + ∠5 = 180° or ∠2 + ∠3 + ∠6 + ∠7 = 180° ............(1)

From above figure,

∠1 + ∠8 = ∠AOD, ∠4 + ∠5 = ∠BOC and ∠2 + ∠3 = ∠AOB, ∠6 + ∠7 = ∠COD

Substituting above values in equation (1), we get :

⇒ ∠AOD + ∠BOC = 180° or ∠AOB + ∠COD = 180°

∠AOD and ∠BOC are angles subtended by opposite sides of quadrilateral circumscribing a circle and the sum of the two is 180°.

Hence, proved that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.