Multiple-Choice Questions

A retailer buys an article at its listed price from a wholesaler and sells it to a consumer in the same state after marking up the price by 20%. The list price of the article is ₹ 2500, and the rate of GST is 12%. What is the tax liability of the retailer to the central government?

1. ₹ 0

2. ₹ 15

3. ₹ 30

4. ₹ 60

Answer

For retailer,

C.P. = ₹ 2500

G.S.T. = 12%

C.G.S.T. = $\dfrac{12}{2}$ % = 6%.

C.G.S.T. paid = $\dfrac{6}{100} \times 2500$ = ₹ 150.

Given,

Retailer sells the article to the consumer in the same state after marking up the price by 20%.

S.P. = ₹ 2500 + 20%

= ₹ 2500 + $\dfrac{20}{100} \times 2500$

= ₹ 2500 + ₹ 500

= ₹ 3000.

C.G.S.T. = 6%

C.G.S.T. charged = $\dfrac{6}{100} \times 3000$ = ₹ 180.

Tax liability = C.G.S.T. charged - C.G.S.T. given

= ₹ 180 - ₹ 150

= ₹ 30.

Hence, Option 3 is the correct option.

Dev brought an electrical fan which has a marked price of ₹ 800. If the GST on the goods is 7%, then the SGST is :

1. ₹ 24

2. ₹ 28

3. ₹ 56

4. ₹ 80

Answer

Since, GST rate is 7%, then SGST = $\dfrac{7}{2}$ = 3.5%.

M.P. of electrical fan = ₹ 800.

SGST = 3.5% of ₹ 800

= $\dfrac{3.5}{100} \times 800$

= ₹ 28.

Hence, Option 2 is the correct option.

₹ P is deposited for n number of months in a recurring deposit account which pays interest at the rate of r% per annum. The nature and time of interest calculated is :

1. compound interest for n number of months

2. simple interest for n number of months

3. compound interest for one month

4. simple interest for one month

Answer

In a recurring deposit account,

By formula,

Interest = $P \times \dfrac{n(n + 1)}{2 \times 12} \times \dfrac{r}{100}$

∴ The nature and time of interest calculated is simple interest for one month.

Hence, Option 4 is the correct option.

Anwesha intended to open a Recurring Deposit account of ₹ 1000 per month for 1 year in a Bank, paying a 5% per annum rate of simple interest. The bank reduced the rate to 4% per annum. How much must Anwesha deposit monthly for 1 year so that her interest remains the same?

1. ₹ 12325

2. ₹ 1250

3. ₹ 1200

4. ₹ 1000

Answer

In first case :

P = ₹ 1000

r = 5%

n = 12 months

Interest = $P \times \dfrac{n(n + 1)}{2 \times 12} \times \dfrac{r}{100}$

$= 1000 \times \dfrac{12 \times (12 + 1)}{2 \times 12} \times \dfrac{5}{100} \\[1em] = 1000 \times \dfrac{12 \times 13}{2 \times 12} \times \dfrac{1}{20} \\[1em] = 25 \times 13 \\[1em] = ₹ 325.$

In second case :

P = ₹ x (Let)

r = 4%

n = 12 months

Interest = ₹ 325

$\therefore 325 = x \times \dfrac{12 \times 13}{2 \times 12} \times \dfrac{4}{100} \\[1em] \Rightarrow 325 = x \times \dfrac{13}{2} \times \dfrac{1}{25}\\[1em] \Rightarrow x = \dfrac{325 \times 25 \times 2}{13} \\[1em] \Rightarrow x = \dfrac{16250}{13} = \text{₹ 1250.}$

Hence, Option 2 is the correct option.

Mr. Das invests in ₹ 100, 12% shares of Company A available at ₹ 60 each. Mr. Singh invests in ₹ 50, 16% shares of Company B available at ₹ 40 each. Use this information to state which of the following statements is true.

1. The rate of return for Mr. Das is 12%

2. The rate of return for Mr. Singh is 10%

3. Both Mr. Das and Mr. Singh have the same rate of return of 10%

4. Both Mr. Das and Mr. Singh have the same rate of return of 20%

Answer

For Mr. Das,

Face value of each share = ₹ 100

Market value of each share = ₹ 60

Dividend per share = 12% of ₹ 100 = ₹ 12.

Rate of return = $\dfrac{\text{Dividend per share}}{\text{M.V. of each share}} \times 100 = \dfrac{12}{60} \times 100$ = 20%.

For Mr. Singh,

Face value of each share = ₹ 50

Market value of each share = ₹ 40

Dividend per share = 16% of ₹ 50 = ₹ 8.

Rate of return = $\dfrac{\text{Dividend per share}}{\text{M.V. of each share}} \times 100 = \dfrac{8}{40} \times 100$ = 20%.

∴ Both Mr. Das and Mr. Singh have the same rate of return of 20%.

Hence, Option 4 is the correct option.

Amit invested a certain sum of money in ₹ 100 shares, paying a 7.5% dividend. The rate of return on his investment is 10%. The money invested by Amit to purchase 10 shares is :

1. ₹ 250

2. ₹ 750

3. ₹ 900

4. ₹ 1100

Answer

Let ₹ P be the price per share.

Amit brought 10 shares, so total investment = ₹ 10P

Dividend = 7.5%

Dividend per share = $\dfrac{7.5}{100} \times 100$ = ₹ 7.5

Total dividend = ₹ 7.5 × 10 = ₹ 75.

Rate of return = 10%

By formula,

Rate of return × Investment = Dividend

$\Rightarrow 10$

Total investment = 10P = 10 × ₹75 = ₹750.

Hence, Option 2 is the correct option.

If -3 ≤ -4x + 5 and x ∈ W, then the solution set is :

1. {.......-3, -2, -1, 0, 1, 2, 3, .......}

2. {1, 2}

3. {0, 1, 2}

4. {2, 3, 4, 5}

Answer

Solving,

⇒ -3 ≤ -4x + 5

⇒ 4x ≤ 5 + 3

⇒ 4x ≤ 8

⇒ x ≤ $\dfrac{8}{4}$

⇒ x ≤ 2.

Since, x ≤ 2 and x ∈ W.

∴ Solution set = {0, 1, 2}.

Hence, Option 3 is the correct option.

If -4x > 8y; then

1. x > 2y

2. x > -2y

3. x < -2y

4. x < 2y

Answer

Solving,

⇒ -4x > 8y

⇒ 4x < -8y

⇒ x < $-\dfrac{8y}{4}$

⇒ x < -2y.

Hence, Option 3 is the correct option.

The value/s of 'k' for which the quadratic equation 2x² - kx + k = 0 has equal roots is (are) :

1. 0 only

2. 4, 0

3. 8 only

4. 0, 8

Answer

Given,

Equation : 2x² - kx + k = 0

a = 2, b = -k and c = k.

For equal roots,

⇒ Discriminant (D) = 0

⇒ b² - 4ac = 0

⇒ (-k)² - 4 × 2 × k = 0

⇒ k² - 8k = 0

⇒ k(k - 8) = 0

⇒ k = 0 or k - 8 = 0

⇒ k = 0 or k = 8.

Hence, Option 4 is the correct option.

If x = -2 is one of the solutions of the quadratic equation x² + 3a - x = 0, then the value of 'a' is :

1. -8

2. -2

3. $-\dfrac{1}{3}$

4. $\dfrac{1}{3}$

Answer

Given,

x = -2 is one of the solutions of the quadratic equation x² + 3a - x = 0.

∴ (-2)² + 3a - (-2) = 0

⇒ 4 + 3a + 2 = 0

⇒ 3a + 6 = 0

⇒ 3a = -6

⇒ a = $-\dfrac{6}{3}$ = -2.

Hence, Option 2 is the correct option.

In solving a quadratic equation, one of the values of the variables x is 233.356. The solution rounded to two significant figures is :

1. 233.36

2. 233.35

3. 233.3

4. 230

Answer

x = 233.356

On rounding off to two significant figures

x = 230.

Hence, Option 4 is the correct option.

In the adjoining diagram, AB = x cm, BC = y cm and x - y = 7 cm. Area of △ ABC = 30 cm². The length of AC is :

1. 10 cm

2. 12 cm

3. 13 cm

4. 15 cm

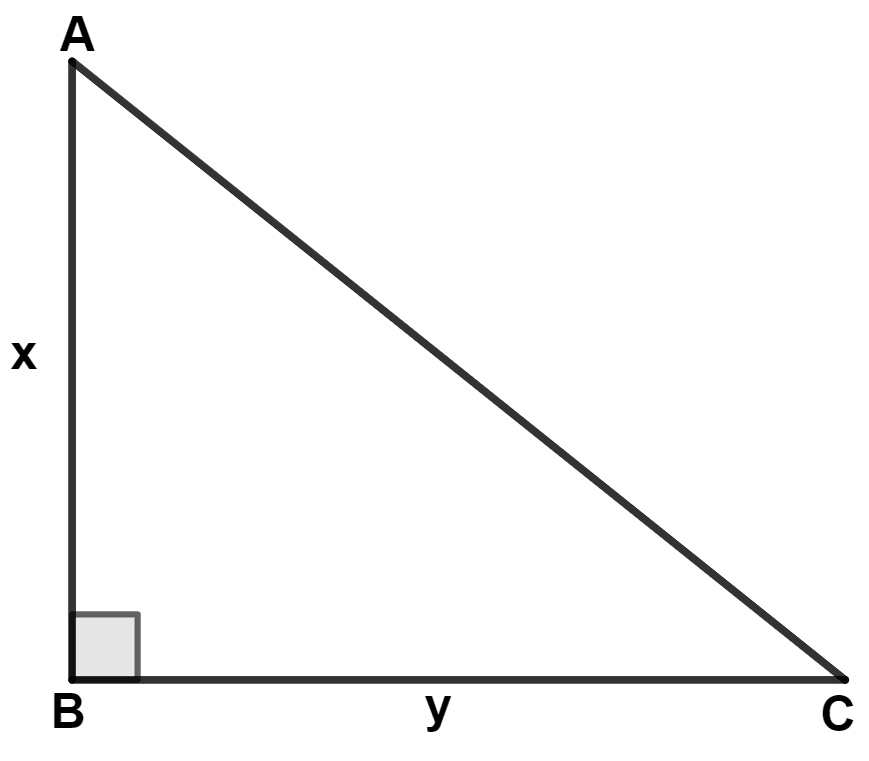
Answer

By formula,

Area of triangle = $\dfrac{1}{2} \times \text{ base} \times \text{height}$

⇒ 30 = $\dfrac{1}{2} \times BC \times AB$

⇒ 30 = $\dfrac{1}{2} \times y \times x$

⇒ 30 = $\dfrac{xy}{2}$

⇒ xy = 60 ........(1)

Given,

⇒ x - y = 7

⇒ x = 7 + y ........(2)

Substituting value of x from equation (2) in (1), we get :

⇒ (7 + y)y = 60

⇒ 7y + y² = 60

⇒ y² + 7y - 60 = 0

⇒ y² + 12y - 5y - 60 = 0

⇒ y(y + 12) - 5(y + 12) = 0

⇒ (y - 5)(y + 12) = 0

⇒ y - 5 = 0 or y + 12 = 0

⇒ y = 5 or y = -12.

Since, side cannot be negative,

∴ y = 5 cm.

Substituting value of y in equation (2), we get :

⇒ x = 7 + y = 7 + 5 = 12 cm.

In right angle triangle ABC,

By pythagoras theorem,

⇒ AC² = AB² + BC²

⇒ AC² = x² + y²

⇒ AC² = 12² + 5²

⇒ AC² = 144 + 25

⇒ AC² = 169

⇒ AC = $\sqrt{169}$ = 13 cm.

Hence, Option 3 is the correct option.

If p, q, and r are in continued proportion, then :

1. p : q = p : r

2. q : r = p² : q²

3. p : q² = r : p²

4. p : r = p² : q²

Answer

Since, p, q, and r are in continued proportion.

$\therefore \dfrac{p}{q} = \dfrac{q}{r} \\[1em] \Rightarrow q^2 = pr \text{ ........(1)}$

Solving,

p : r = p² : q²

$\Rightarrow \dfrac{p}{r} = \dfrac{p^2}{q^2} \\[1em] \Rightarrow q^2 = \dfrac{p^2 \times r}{p} \\[1em] \Rightarrow q^2 = pr \text{ .........(2)}$

Since, equation (1) and (2) are equal.

Hence, Option 4 is the correct option.

The ratio of diameter to height of a Borosil cylindrical glass is 3 : 5. If the actual diameter of the glass is 6 cm, then the curved surface area of the glass is :

1. 120π

2. 60π

3. 30π

4. 18π

Answer

Given,

Ratio of diameter to height of a Borosil cylindrical glass is 3 : 5.

$\Rightarrow \dfrac{d}{h} = \dfrac{3}{5} \\[1em] \Rightarrow \dfrac{6}{h} = \dfrac{3}{5} \\[1em] \Rightarrow h = \dfrac{6 \times 5}{3} \\[1em] \Rightarrow h = 10 \text{ cm}.$

Radius = $\dfrac{\text{Diameter}}{2} = \dfrac{6}{2}$ = 3 cm.

By formula,

Curved surface area of glass = 2πrh

= 2π × 3 × 10

= 60π cm².

Hence, Option 2 is the correct option.

If the polynomial 2x³ + 3x² - 2x - 3 is completely divisible by (2x + a), and the quotient is equal to (x² - 1), then one of the values of a is :

1. -3

2. -1

3. 1

4. 3

Answer

Given,

The polynomial 2x³ + 3x² - 2x - 3 is completely divisible by (2x + a) and quotient is equal to (x² - 1).

∴ 2x³ + 3x² - 2x - 3 = (2x + a)(x² - 1)

⇒ 2x³ + 3x² - 2x - 3 = 2x³ - 2x + ax² - a

⇒ 2x³ - 2x³ + 3x² - 2x + 2x - 3 = ax² - a

⇒ 3x² - 3 = ax² - a

From above equation,

a = 3.

Hence, Option 4 is the correct option.

A polynomial in x is x³ + 5x² - kx - 24. Which of the following is a factor of the given polynomial so that the value of k is 2?

1. (x + 2)

2. (x - 3)

3. (x + 4)

4. (x - 4)

Answer

By factor theorem,

(x - a) is a factor of f(x), if f(a) = 0.

Given,

Polynomial = x³ + 5x² - kx - 24

If k = 2, then :

Polynomial = x³ + 5x² - 2x - 24.

Dividing polynomial by (x + 4) or substituting -4 in polynomial, we get :

⇒ (-4)³ + 5(-4)² - 2(-4) - 24

⇒ -64 + 5(16) + 8 - 24

⇒ -64 + 80 + 8 - 24

⇒ 88 - 88

⇒ 0.

Since, on substituting -4 in polynomial, we get remainder = 0.

∴ (x + 4) is the factor of x³ + 5x² - kx - 24, when k = 2.

Hence, Option 3 is the correct option.

If A = $\begin{bmatrix*}[r] a & b \end{bmatrix*} \text{ and } \begin{bmatrix*}[r] c \\ d \end{bmatrix*}$, then :

1. only matrix AB is possible

2. only matrix BA is possible

3. both matrices AB and BA are possible

4. both matrices AB and BA are possible, AB = BA

Answer

Order of matrix A = 1 × 2

Order of matrix B = 2 × 1

Since, no. of columns in A is equal to the no. of rows in B and no. of columns in B is equal to the no. of rows in A.

∴ AB and BA are possible.

$AB = \begin{bmatrix*}[r] a \times c + b \times d \end{bmatrix*} \\[1em] = \begin{bmatrix*}[r] ac + bd \end{bmatrix*}. \\[1em] BA = \begin{bmatrix*}[r] c \times a & c \times b \\ d \times a & d \times b \end{bmatrix*} \\[1em] = \begin{bmatrix*}[r] ca & cb \\ da & db \end{bmatrix*}.$

∴ AB ≠ BA.

Hence, Option 3 is the correct option.

Matrix A = $\begin{bmatrix*}[r] 6 & 9 \\ -4 & k \end{bmatrix*} \text{ such that } A^2 = \begin{bmatrix*}[r] 0 & 0 \\ 0 & 0 \end{bmatrix*}$. Then k is :

1. 6

2. -6

3. 36

4. ±6

Answer

Given, $A^2 = \begin{bmatrix*}[r] 0 & 0 \\ 0 & 0 \end{bmatrix*}$.

$\therefore \begin{bmatrix*}[r] 6 & 9 \\ -4 & k \end{bmatrix*}\begin{bmatrix*}[r] 6 & 9 \\ -4 & k \end{bmatrix*} = \begin{bmatrix*}[r] 0 & 0 \\ 0 & 0 \end{bmatrix*} \\[1em] \Rightarrow \begin{bmatrix*}[r] 6 \times 6 + 9 \times (-4) & 6 \times 9 + 9 \times k \\ -4 \times 6 + k \times (-4) & (-4) \times 9 + k \times k \end{bmatrix*} = \begin{bmatrix*}[r] 0 & 0 \\ 0 & 0 \end{bmatrix*} \\[1em] \Rightarrow \begin{bmatrix*}[r] 36 + (-36) & 54 + 9k \\ -24 - 4k & -36 + k^2 \end{bmatrix*} = \begin{bmatrix*}[r] 0 & 0 \\ 0 & 0 \end{bmatrix*} \\[1em] \Rightarrow \begin{bmatrix*}[r] 0 & 54 + 9k \\ -24 - 4k & -36 + k^2 \end{bmatrix*} = \begin{bmatrix*}[r] 0 & 0 \\ 0 & 0 \end{bmatrix*} \\[1em] \Rightarrow 54 + 9k = 0 \\[1em] \Rightarrow 9k = -54 \\[1em] \Rightarrow k = -\dfrac{54}{9} = -6.$

Hence, Option 2 is the correct option.

If the sum of n terms of an arithmetic progression S_n = n² - n, then the third term of the series is :

1. 2

2. 4

3. 6

4. 9

Answer

Given,

Sum of n terms of an arithmetic progression S_n = n² - n.

S₁ = 1² - 1 = 0,

S₂ = 2² - 2 = 4 - 2 = 2,

S₃ = 3² - 3 = 9 - 3 = 6.

Sum upto first term = First term = 0.

Given, sum upto 2 terms = 2 and first term = 0, second term = 2.

Sum upto third term = 6

∴ First term + Second term + Third term = 6

⇒ 0 + 2 + Third term = 6

⇒ Third term = 6 - 2 = 4.

Hence, Option 2 is the correct option.

Which of the following is not a geometric progression ?

1. $\dfrac{1}{3}, 1, 3, 9$

2. $\dfrac{1}{5}, \dfrac{1}{5}, \dfrac{1}{5}, \dfrac{1}{5}$

3. -2, 4, -8, 16

4. 2, 0, 4, 0, 8, 0

Answer

In the series,

2, 0, 4, 0, 8, 0

$\dfrac{0}{2} \ne \dfrac{4}{0}$

∴ 2, 0, 4, 0, 8, 0 is not a G.P.

Hence, Option 4 is the correct option.

In the adjoining diagram, G is the centroid of △ ABC. A(3, -3), B(2, -6), C(x, y) and G(5, -5). The coordinates of point D are :

1. (2, -6)

2. (3, -6)

3. (6, -6)

4. (10, -6)

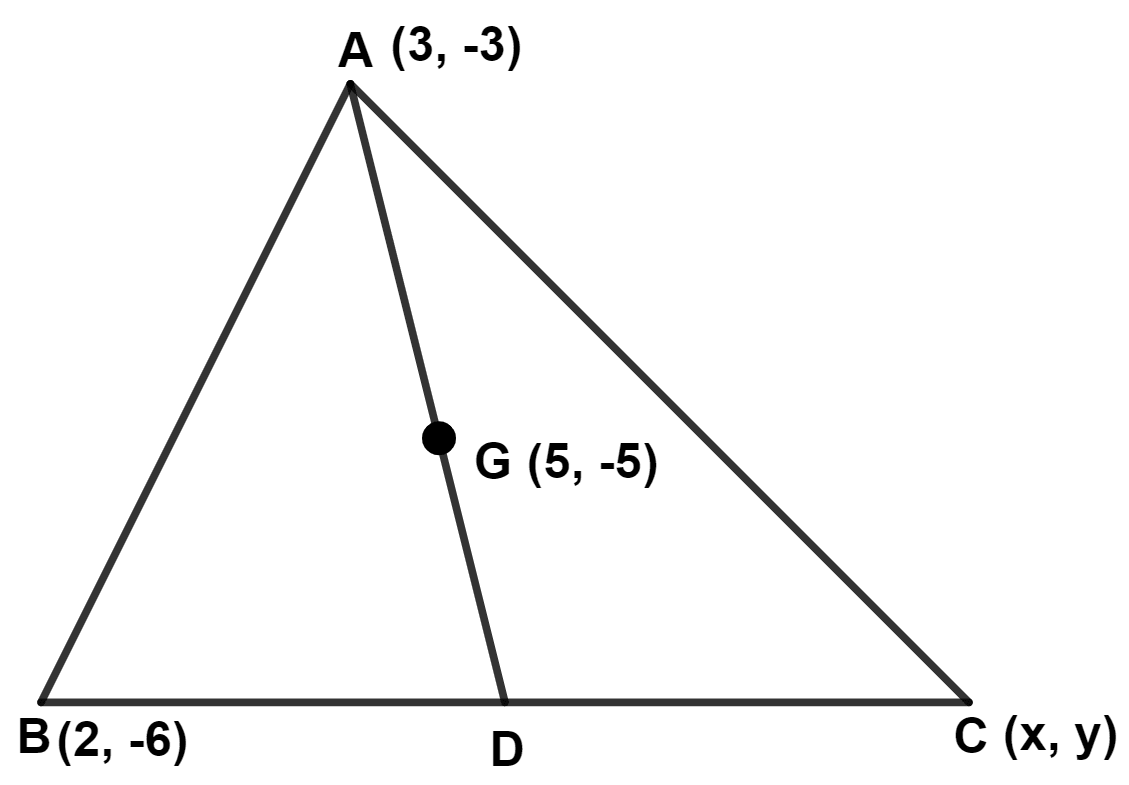
Answer

By formula,

Centroid of triangle = $\Big(\dfrac{x_1 + x_2 + x_3}{3}, \dfrac{y_1 + y_2 + y_3}{3}\Big)$

$\therefore (5, -5) = \Big(\dfrac{3 + 2 + x}{3}, \dfrac{(-3) + (-6) + y}{3}\Big) \\[1em] \Rightarrow (5, -5) = \Big(\dfrac{x + 5}{3}, \dfrac{y - 9}{3}\Big) \\[1em] \Rightarrow \dfrac{x + 5}{3} = 5 \text{ and } \dfrac{y - 9}{3} = -5 \\[1em] \Rightarrow x + 5 = 15 \text{ and } y - 9 = -15 \\[1em] \Rightarrow x = 15 - 5 = 10 \text{ and } y = -15 + 9 = -6.$

C(x, y) = (10, -6).

Since, centroid is the point of intersection of all the three medians of a triangle.

∴ AD is the median.

∴ D is mid-point of BC.

$D = \Big(\dfrac{2 + 10}{2}, \dfrac{(-6) + (-6)}{2}\Big) \\[1em] = \Big(\dfrac{12}{2}, \dfrac{-12}{2}\Big) \\[1em] = (6, -6).$

Hence, Option 3 is the correct option.

In the given diagram, O is the origin and P is the mid-point of AB. The equation of OP is :

1. y = x

2. 2y = x

3. y = 2x

4. y = -x

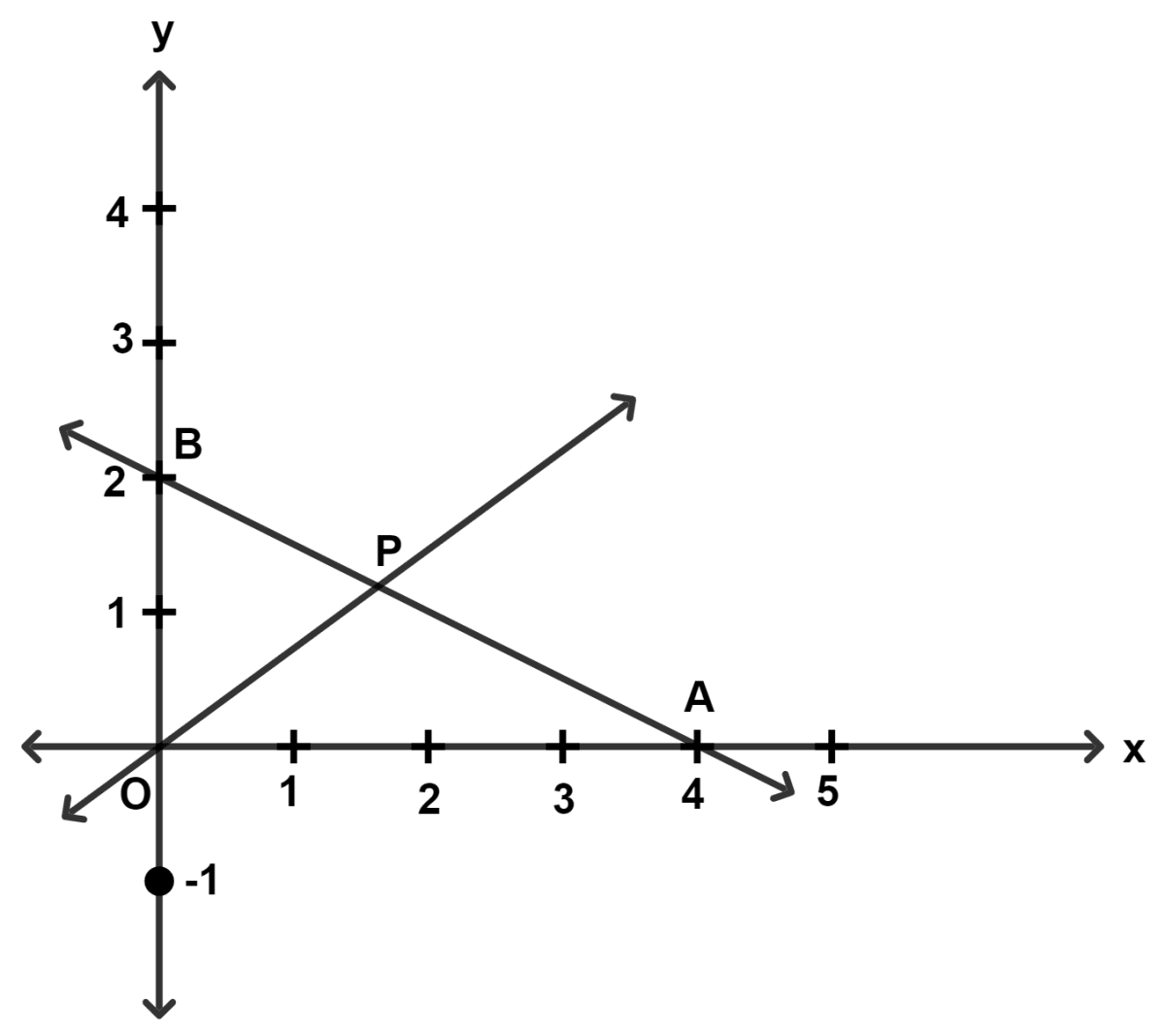
Answer

From graph,

A = (4, 0) and B = (0, 2).

Given,

P is the mid-point of AB.

P = $\Big(\dfrac{4 + 0}{2}, \dfrac{0 + 2}{2}\Big) = \Big(\dfrac{4}{2}, \dfrac{2}{2}\Big)$ = (2, 1).

By two-point form,

⇒ y - y₁ = $\dfrac{y_2 - y_1}{x_2 - x_1}(x - x_1)$

⇒ y - 1 = $\dfrac{1 - 0}{2 - 0}(x - 2)$

⇒ y - 1 = $\dfrac{1}{2}(x - 2)$

⇒ 2(y - 1) = x - 2

⇒ 2y - 2 = x - 2

⇒ 2y = x - 2 + 2

⇒ 2y = x.

Hence, Option 2 is the correct option.

In the given figure line l₁ is a parallel to line l₂. If line l₃ is perpendicular to line l₁, then the slopes of lines l₂ and l₃ respectively are :

1. 1, 1

2. -1, -1

3. 1, -1

4. -1, 1

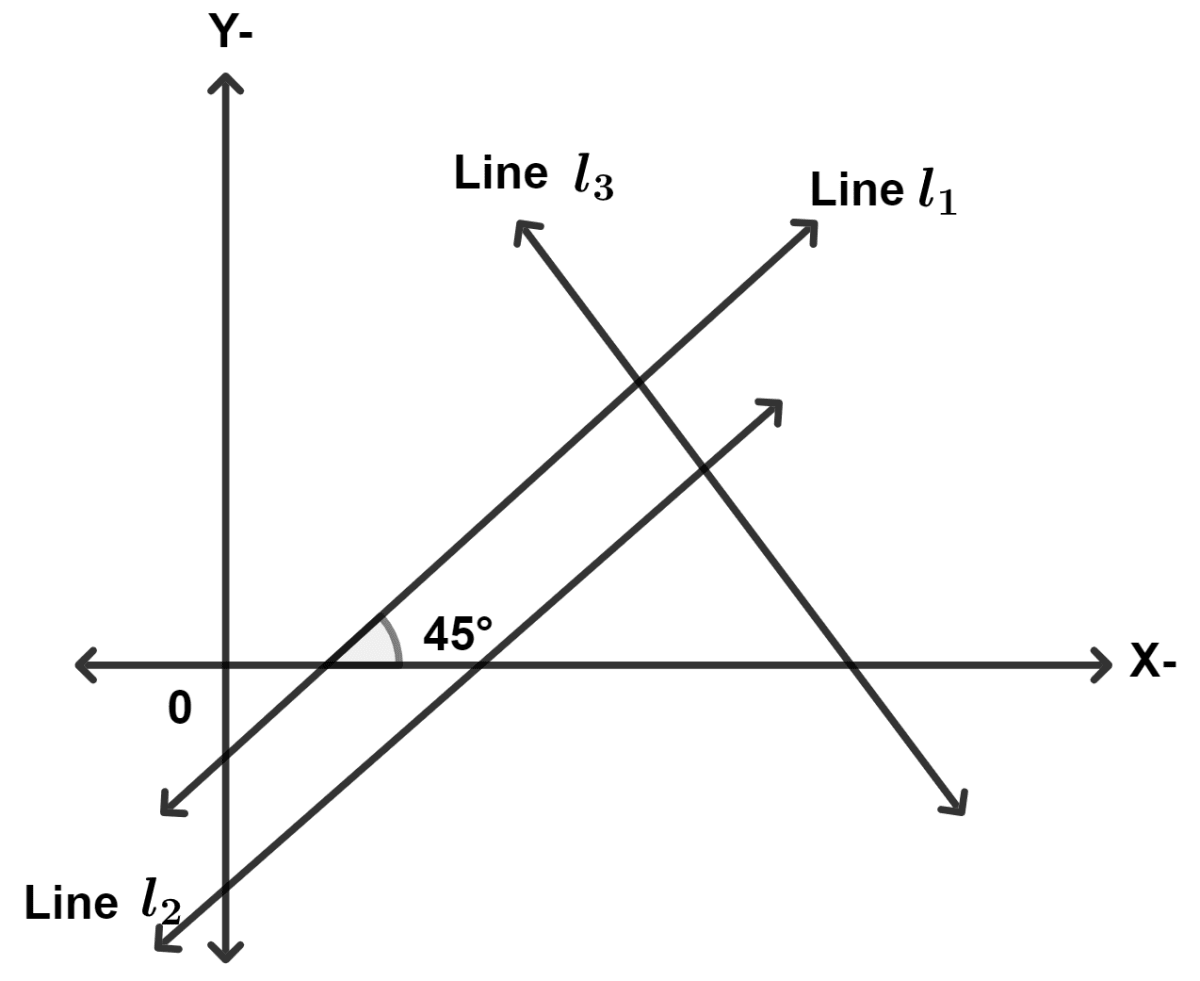
Answer

Slope of line l₁ = tan 45° = 1.

We know that,

Slope of parallel lines are equal.

Slope of line l₂ = Slope of line l₁ = 1.

We know that,

Product of slope of perpendicular lines is equal to -1.

⇒ Slope of line l₂ × Slope of line l₃ = -1

⇒ 1 × Slope of line l₃ = -1

⇒ Slope of line l₃ = -1.

Hence, Option 3 is the correct option.

Which of the following lines cut the positive x-axis and positive y-axis at equal distances form the origin?

1. 3x + 3y = 6

2. 5x + 10y = 10

3. -x + y = 1

4. 10x + 5y = 5

Answer

Substituting x = 0 in first equation,

⇒ 3(0) + 3y = 6

⇒ 3y = 6

⇒ y = $\dfrac{6}{3}$

⇒ y = 2.

The line touches y-axis at point (0, 2).

Substituting y = 0 in first equation,

⇒ 3x + 3(0) = 6

⇒ 3x = 6

⇒ x = $\dfrac{6}{3}$

⇒ x = 2.

The line touches y-axis at point (2, 0).

∴ Line 3x + 3y = 6 cuts positive x-axis and positive y-axis at equal distance i.e. 2 units form the origin.

Hence, Option 1 is the correct option.

In the given diagram (not draw to scale), railway stations A, B, C, P and Q are connected by straight tracks. Track PQ is parallel to BC. The time taken by a train travelling at 90 km/hr to reach B from A by the shortest route is :

1. 8 minutes

2. 12 minutes

3. 16.8 minutes

4. 20 minutes

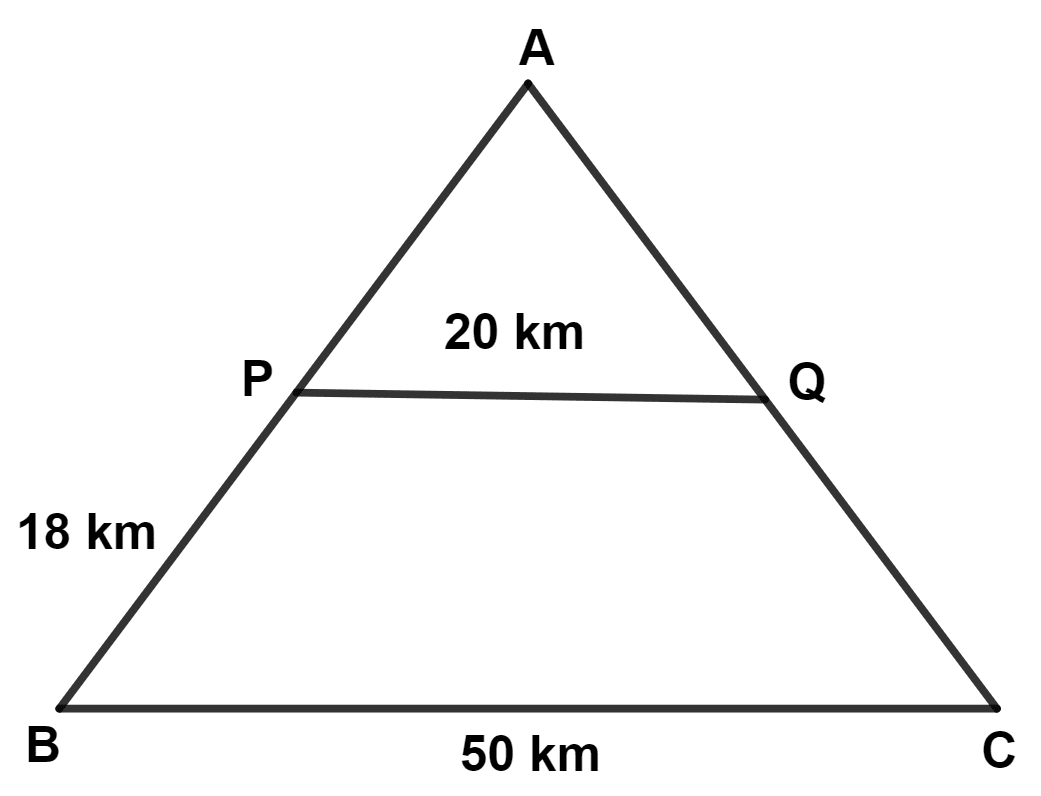
Answer

In △ APQ and △ ABC,

⇒ ∠PAQ = ∠BAC (Common angle)

⇒ ∠APQ = ∠ABC (Corresponding angles are equal)

∴ △ APQ ~ △ ABC (By A.A. axiom)

From figure,

Let AP = x km.

We know that,

Corresponding sides of similar triangle are proportional.

$\Rightarrow \dfrac{AP}{AB} = \dfrac{PQ}{BC} \\[1em] \Rightarrow \dfrac{x}{AP + PB} = \dfrac{20}{50} \\[1em] \Rightarrow \dfrac{x}{x + 18} = \dfrac{2}{5} \\[1em] \Rightarrow 5x = 2(x + 18) \\[1em] \Rightarrow 5x = 2x + 36 \\[1em] \Rightarrow 5x - 2x = 36 \\[1em] \Rightarrow 3x = 36 \\[1em] \Rightarrow x = \dfrac{36}{3} \\[1em] \Rightarrow x = 12.$

AB = AP + BP = 12 + 18 = 30 km.

Time = $\dfrac{\text{Distance}}{\text{Speed}} = \dfrac{AB}{90} = \dfrac{30}{90} = \dfrac{1}{3} \text{ hr} = \dfrac{1}{3} \times 60$ = 20 minutes.

Hence, Option 4 is the correct option.

In the given diagram, △ ABC and △ DEF (not drawn to scale) are such that ∠C = ∠F and $\dfrac{AB}{DE} = \dfrac{BC}{EF}$, then

1. △ ABC ~ △ DEF

2. △ BCA ~ △ DEF

3. △ CAB ~ △ DEF

4. the similarity of given triangles cannot be determined.

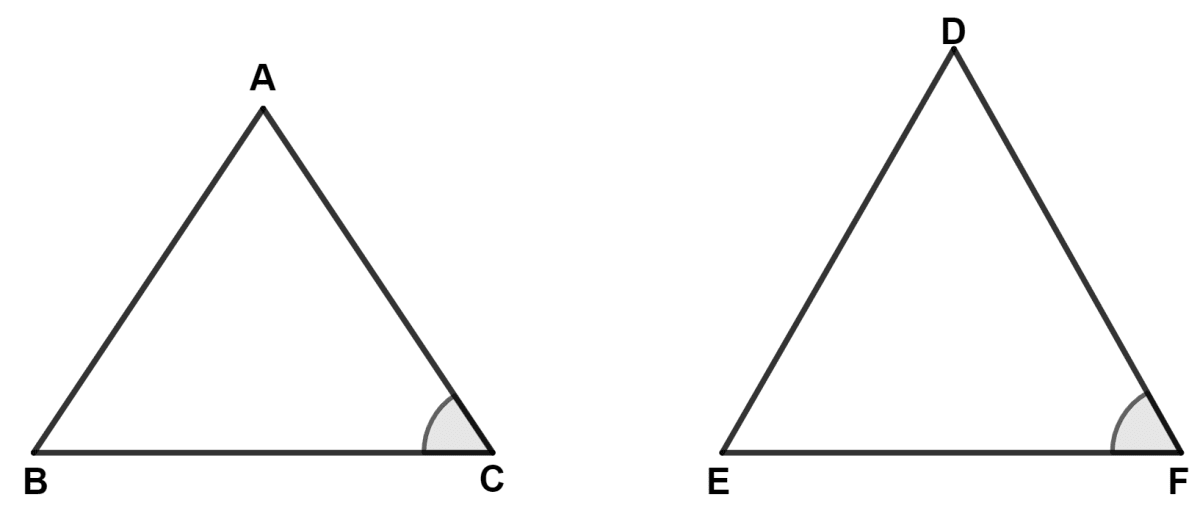
Answer

Given,

⇒ ∠C = ∠F

Since, the sides containing the angle may or may not be proportional,

i.e., we don't know if $\dfrac{AC}{DF}$ and $\dfrac{BC}{EF}$ are equal or not equal.

∴ Similarity of given triangles cannot be determined.

Hence, Option 4 is the correct option.

In the adjoining diagram, ST is not parallel to PQ. The necessary and sufficient conditions for △ PQR ~ △ TSR is :

1. ∠PQR = ∠STR

2. ∠QPR = ∠TSR

3. ∠PQR = ∠TSR

4. ∠PRQ = ∠RST

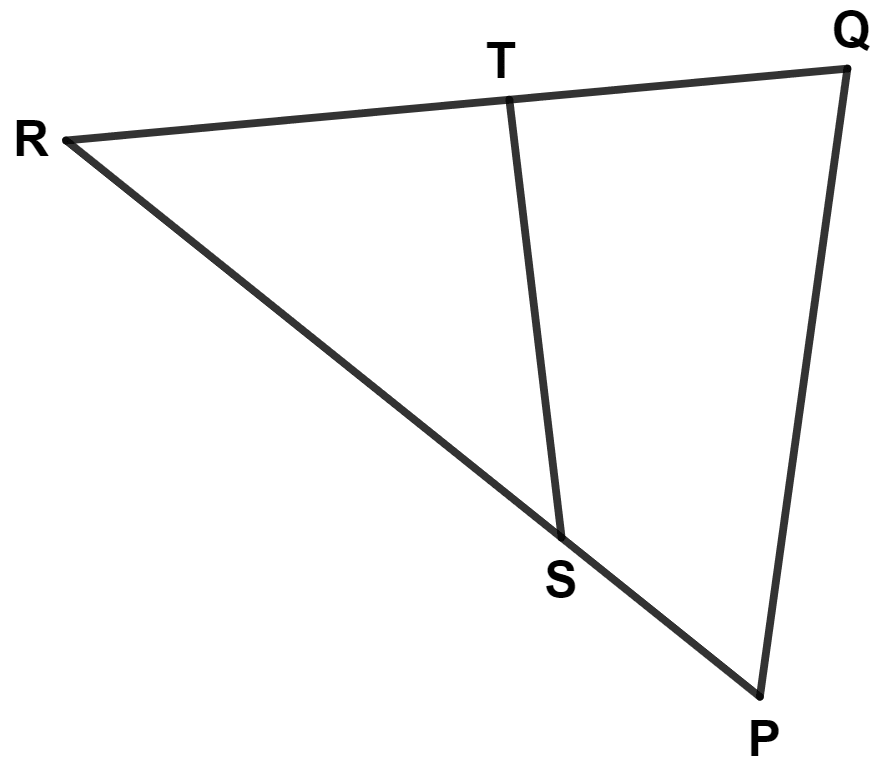
Answer

Given,

△ PQR ~ △ TSR.

From figure,

⇒ ∠PRQ = ∠SRT (Common angle)

The order of vertices of two similar triangles are written in such a way that the corresponding vertices occupy the same position.

∴ ∠PQR = ∠TSR

∴ △ PQR ~ △ TSR (By A.A. axiom)

Hence, Option 3 is the correct option.

The scale factor of a picture and the actual height of Sonia is 20 cm : 1.6 m. If her height in the picture is 18 cm, then her actual height is :

1. 14.4 m

2. 2.25 m

3. 1.78 m

4. 1.44 m

Answer

Scale factor of a picture and the actual height = 20 cm : 1.6 m = 20 cm : 160 cm

$\therefore \dfrac{\text{Height in picture}}{\text{Actual height}} = \dfrac{\text{20 cm}}{\text{160 cm}} \\[1em] \Rightarrow \dfrac{18}{\text{Actual height}} = \dfrac{\text{20 cm}}{\text{160 cm}} \\[1em] \Rightarrow \text{Actual height} = \dfrac{18 \times 160}{20} = \text{144 cm} = 1.44 \text{ m}.$

Hence, Option 4 is the correct option.

In the adjoining figure, O is the center of the circle, and a semicircle is drawn on OA as the diameter. ∠APQ = 20°. The degree measure of ∠OAQ is :

1. 25°

2. 40°

3. 50°

4. 65°

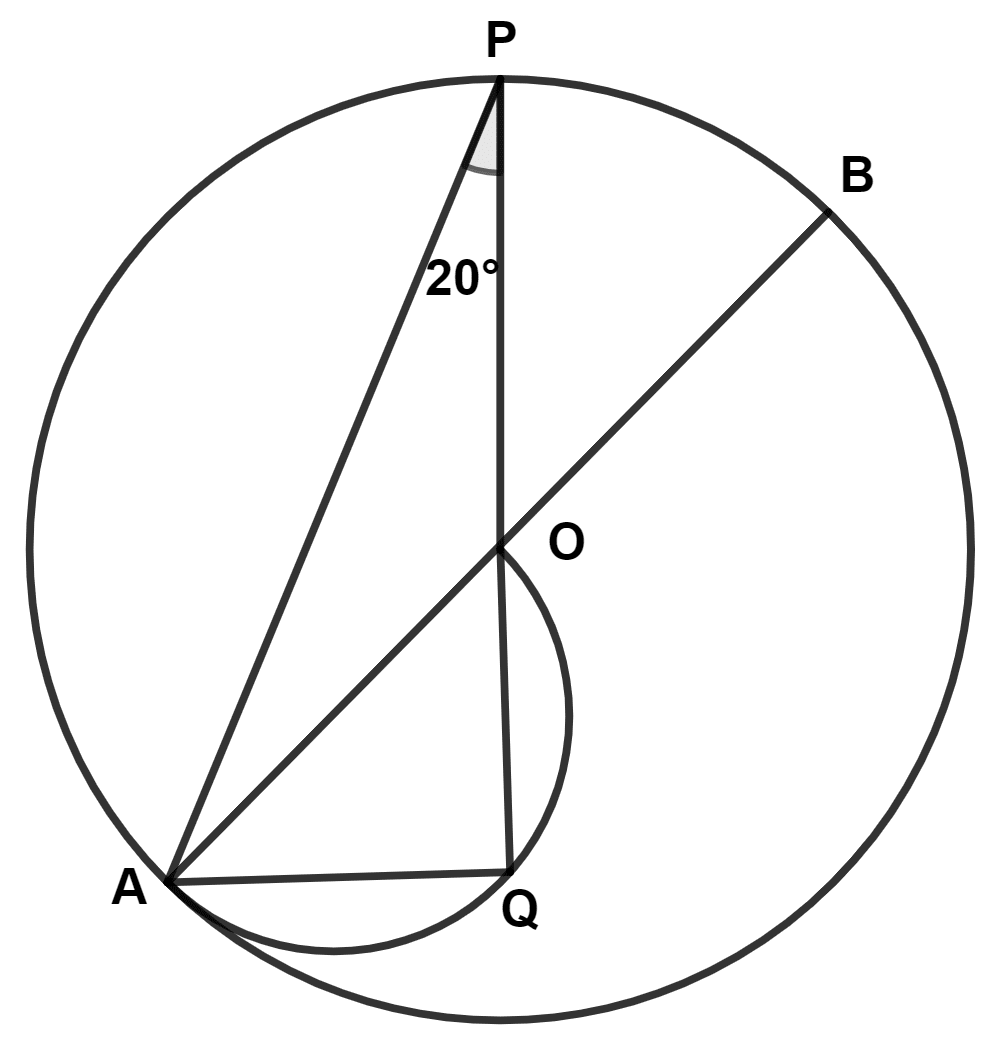
Answer

We know that,

Angle in a semi-circle is a right angle.

∴ ∠OQA = 90°

In △QAP,

⇒ ∠PQA + ∠QAP + ∠APQ = 180°

⇒ 90° + ∠QAP + 20° = 180°

⇒ ∠QAP = 180° - 90° - 20° = 70°.

In △OPA,

⇒ OA = OP (Radii of same circle)

⇒ ∠OAP = ∠OPA (Angle opposite to equal sides are equal)

⇒ ∠OAP = 20°.

From figure,

⇒ ∠OAQ = ∠QAP - ∠OAP = 70° - 20° = 50°.

Hence, Option 3 is the correct option.

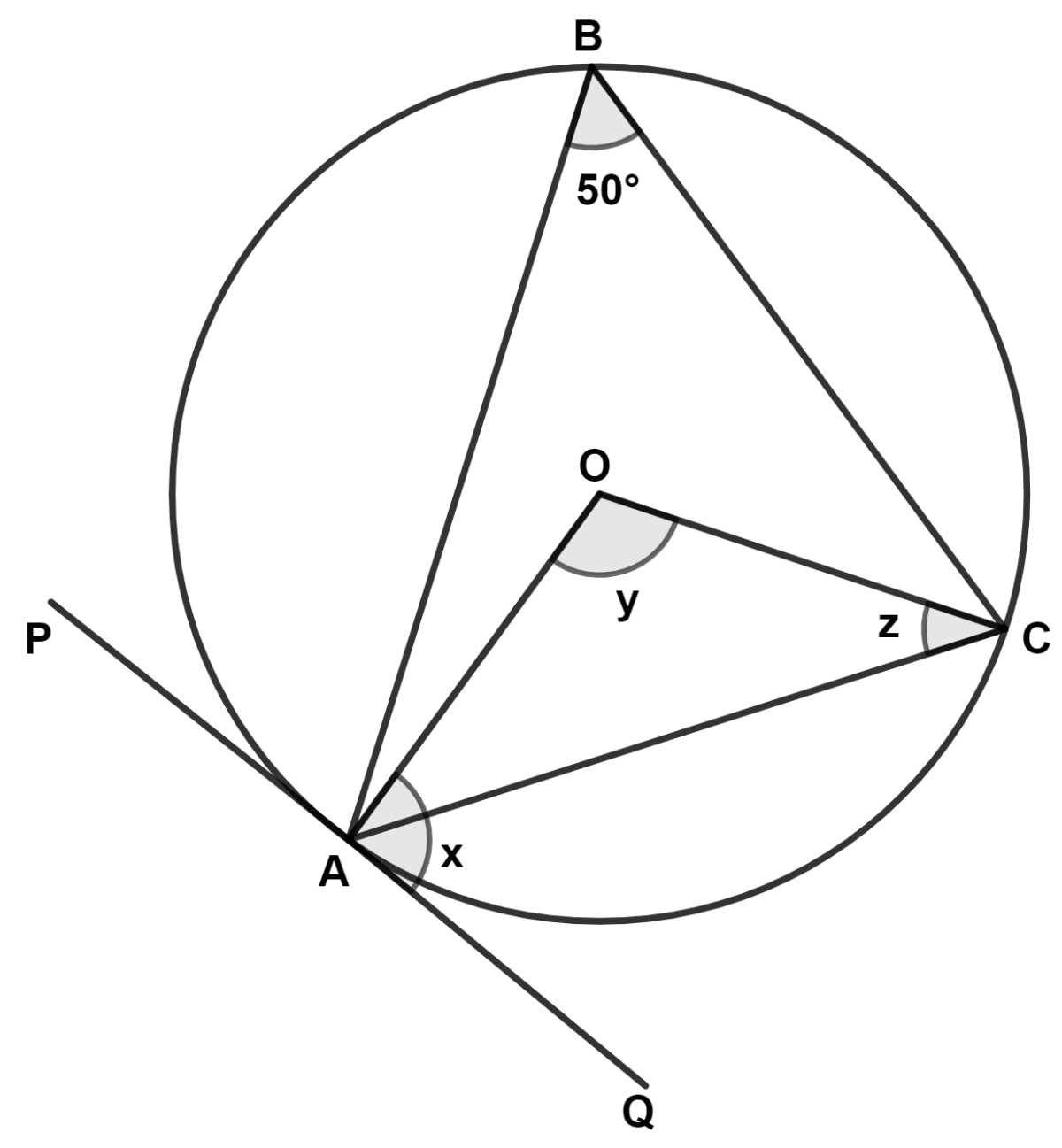
In the given diagram, O is the center of the circle, and PQ is a tangent at A. If ∠ABC = 50°, then values of x, y and z respectively are :

1. 50°, 100°, 40°

2. 50°, 50°, 65°

3. 40°, 80°, 50°

4. 50°, 25°, 78°

Answer

We know that,

The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.

∴ ∠AOC (y) = 2∠ABC = 2 × 50° = 100°.

In △ AOC,

⇒ OA = OC (Radii of same circle)

⇒ ∠OAC = ∠OCA = z (Angle opposite to equal sides are equal)

By angle sum property of triangle,

⇒ ∠OAC + ∠OCA + ∠AOC = 180°

⇒ z + z + 100° = 180°

⇒ 2z = 180° - 100°

⇒ 2z = 80°

⇒ z = $\dfrac{80°}{2}$ = 40°.

We know that,

The tangent at any point of a circle is perpendicular to the radius through the point of contact.

⇒ ∠CAQ (x) = ∠OAQ - ∠OAC = 90° - 40° = 50°.

Hence, Option 1 is the correct option.

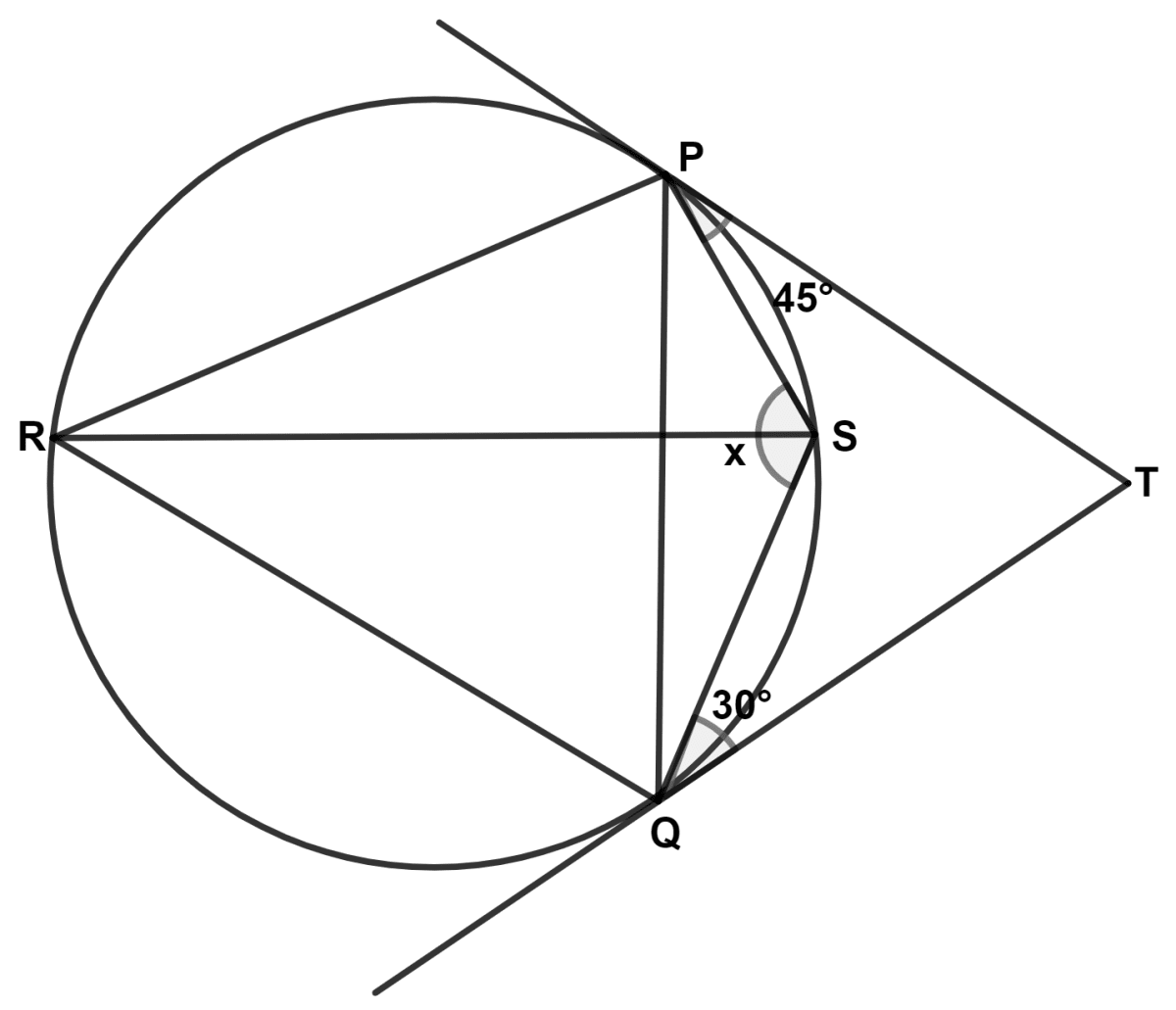
In the given figure, PT and QT are tangents to a circle such that ∠TPS = 45° and ∠TQS = 30°. Then, the value of x is :

1. 30°

2. 45°

3. 75°

4. 105°

Answer

We know that,

The angle between a tangent and a chord through point of contact is equal to an angle in the alternate segment.

∴ ∠SQP = ∠SPT = 45° and ∠SPQ = ∠SQT = 30°.

In △ SQP,

⇒ ∠SQP + ∠SPQ + ∠QSP = 180°

⇒ 45° + 30° + ∠QSP = 180°

⇒ 75° + ∠QSP = 180°

⇒ ∠QSP (x) = 180° - 75° = 105°.

Hence, Option 4 is the correct option.

A cylindrical metallic wire is stretched to double its length. Which of the following will NOT change for the wire after stretching?

1. Its curved surface area

2. Its total surface area

3. Its volume

4. Its radius

Answer

On changing the shape of a container, its volume remains same.

Hence, Option 3 is the correct option.

A right circular cone has the radius of the base equal to the height of the cone. If the volume of the cone is 9702 cu. cm, then the diameter of the base of the cone is :

1. 21 cm

2. 42 cm

3. $21\sqrt{7}$ cm

4. $2\sqrt{7}$ cm

$\Big[\text{Use } \pi = \dfrac{22}{7}\Big]$

Answer

Given,

Height of cone (h) = Radius of cone (r) = a cm (let)

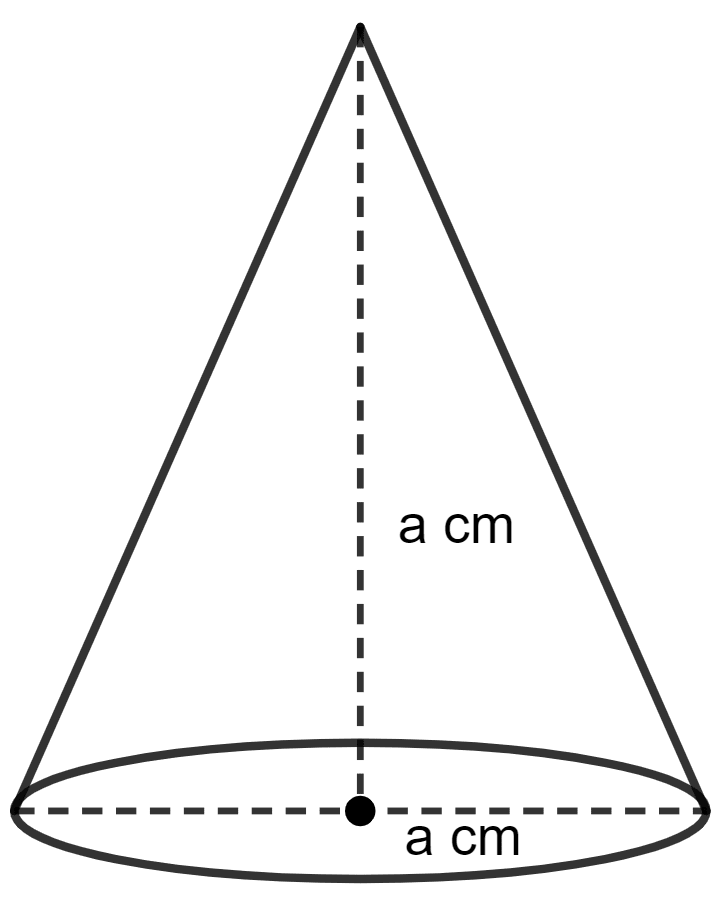
Given,

Volume = 9702 cm³

$\therefore \dfrac{1}{3}πr^2h = 9702 \\[1em] \Rightarrow \dfrac{1}{3} \times \dfrac{22}{7} \times a^2 \times a = 9702 \\[1em] \Rightarrow a^3 = \dfrac{9702 \times 7 \times 3}{22} \\[1em] \Rightarrow a^3 = 441 \times 21 \\[1em] \Rightarrow a^3 = 9261 \\[1em] \Rightarrow a = \sqrt[3]{9261} = 21 \text{ cm}.$

Diameter = 2 × radius = 2 × 21 = 42 cm.

Hence, Option 2 is the correct option.

A solid sphere with a radius of 4 cm is cut into 4 identical pieces by two mutually perpendicular planes passing through its center. Find the total surface area of one-quarter piece.

1. 24π

2. 32π

3. 48π

4. 64π

Answer

Total surface area of semi-hemisphere = 2πr²

= 2π × 4²

= 2π × 16

= 32π.

Hence, Option 2 is the correct option.

Two identical solid hemispheres are kept in contact to form a sphere. The ratio of the total surface areas of two hemispheres to the surface area of the sphere formed is :

1. 1 : 1

2. 3 : 2

3. 2 : 3

4. 2 : 1

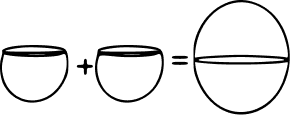
Answer

Let radius of hemisphere be r.

Total surface area of hemisphere = 3πr²

Total surface area of two hemisphere = 2 × 3πr² = 6πr².

Total surface area of sphere = 4πr²

Total surface area of two hemisphere : Total surface area of sphere = 6πr² : 4πr²

= 6 : 4

= 3 : 2.

Hence, Option 2 is the correct option.

cosec² θ + sec² θ is equal to :

1. tan² θ + cot² θ

2. cot θ + tan θ

3. (cot θ + tan θ)²

4. 1

Answer

Solving,

    cosec² θ + sec² θ

= 1 + cot² θ + 1 + tan² θ

= cot² θ + tan² θ + 2

= (cot θ + tan θ)²

Hence, Option 3 is the correct option.

Given a = 3 sec² θ and b = 3 tan² θ - 2. The value of (a - b) is :

1. 1

2. 2

3. 3

4. 5

Answer

    a - b = 3 sec² θ - (3 tan² θ - 2)

= 3 sec² θ - 3 tan² θ + 2

= 3(sec² θ - tan² θ) + 2

= 3(1) + 2

= 3 + 2

= 5.

Hence, Option 4 is the correct option.

At a certain time of day, the ratio of the height of the pole to the length of its shadow is 1 : $\sqrt{3}$, then the angle of elevation of the sun at that time of the day is :

1. 30°

2. 45°

3. 60°

4. 90°

Answer

Let AB be the pole and BC be the shadow and angle of elevation of Sun be θ.

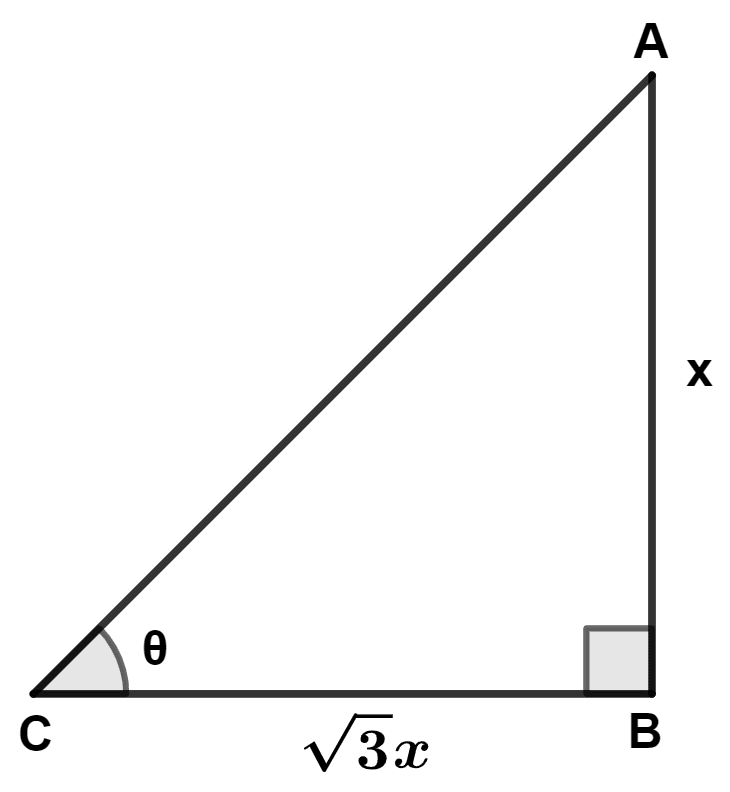
From figure,

⇒ tan θ = $\dfrac{AB}{BC}$

⇒ tan θ = $\dfrac{x}{\sqrt{3}x}$

⇒ tan θ = $\dfrac{1}{\sqrt{3}}$

⇒ tan θ = tan 30°

⇒ θ = 30°.

Hence, Option 1 is the correct option.

A man standing on a ship approaching the port towards the lighthouse is observing the top of the lighthouse. In 10 minutes, the angle of elevation of the top of the lighthouse changes from α to β. Then :

1. α > β

2. α < β

3. α = β

4. α ≤ β

Answer

Let A be the top of the lighthouse, C the initial position of ship and D be the position after 10 minutes.

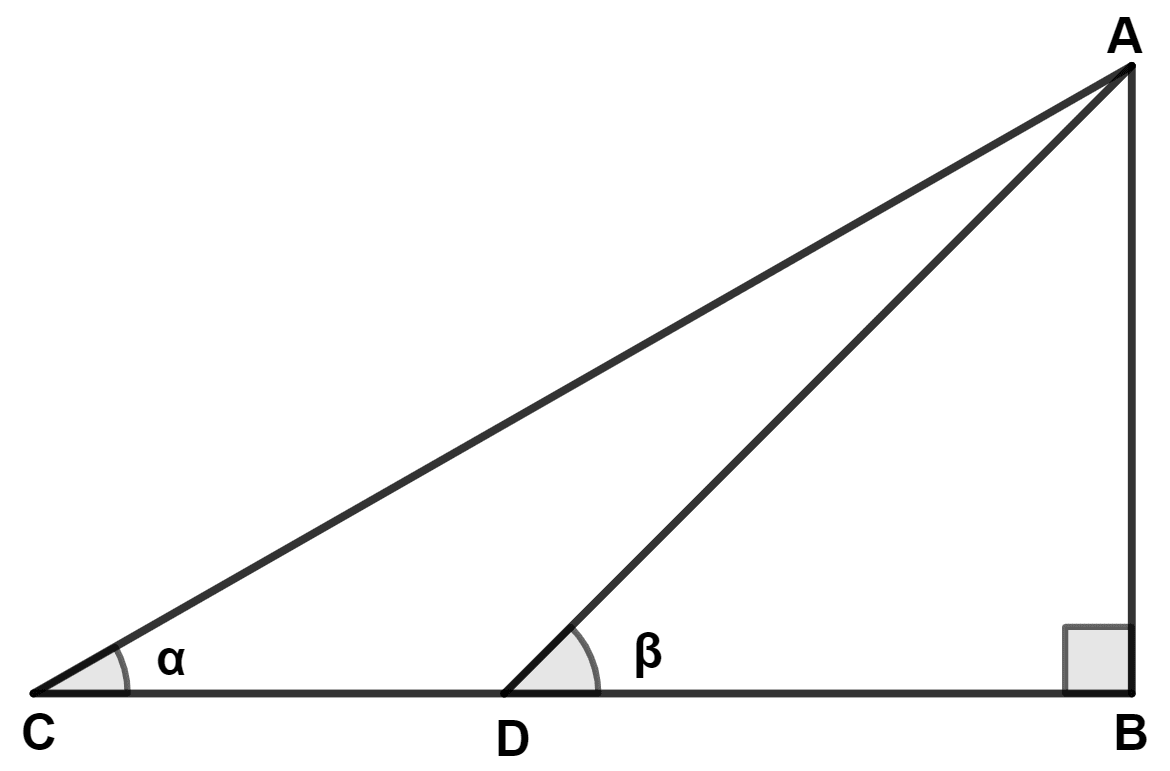
From figure,

tan α = $\dfrac{AB}{BC}$

tan β = $\dfrac{AB}{BD}$

Since, BC is greater than BD.

∴ tan α < tan β

⇒ α < β.

Hence, Option 2 is the correct option.

Assertion (A) : The difference in class marks of the modal class and the median class of the following frequency distribution table is 0.

Reason (R) : Modal class and median class are always the same for a given frequency distribution.

1. Both A and R are correct, and R is the correct explanation for A.

2. Both A and R are correct, and R is not the correct explanation for A.

3. A is true, but R is false.

4. Both A and R are true.

Answer

Cumulative frequency distribution table :

Median = $\dfrac{16}{2}$ = 8th term.

The 8th term lies in the class 50-60.

∴ Median class = 50-60

Also, frequency of class 50-60 is highest.

∴ Modal class = 50-60.

∴ Assertion (A) is true.

Modal class and median class are not always the same for a given frequency distribution.

∴ Reason (R) is false.

Hence, Option 3 is the correct option.

Assertion (A) : For a collection of 11 arrayed data, the median is the middle number.

Reason (R) : For the data 5, 9, 7, 13, 10, 11, 10, the median is 13.

1. Both A and R are correct, and R is the correct explanation for A.

2. Both A and R are correct, and R is not the correct explanation for A.

3. A is true, but R is false.

4. Both A and R are true.

Answer

For 11 arrayed data.

Median = $\dfrac{n + 1}{2}$ th term

= $\dfrac{11 + 1}{2}$

= 6th term, which will be the middle term.

∴ For a collection of 11 arrayed data, the median is the middle number.

∴ Assertion (A) is true.

Numbers = 5, 9, 7, 13, 10, 11, 10

Arranging in ascending order, we get :

5, 7, 9, 10, 10, 11, 13.

n = 7, which is odd.

Median = $\dfrac{n + 1}{2} = \dfrac{7 + 1}{2} = \dfrac{8}{2}$ = 4th term = 10.

∴ Reason (R) is false.

Hence, Option 3 is the correct option.

Ankit has the option of investing in company A, where 7%, ₹ 100 shares are available at ₹ 120 or in company B, where 8%, ₹ 1000 shares are available at ₹ 1620.

Assertion (A) : Investment in Company A is better than Company B.

Reason (R) : The rate of income in Company A is better than in Company B.

1. Both A and R are correct, and R is the correct explanation for A.

2. Both A and R are correct, and R is not the correct explanation for A.

3. A is false, but R is true.

4. Both A and R are false.

Answer

In company A,

N.V. = ₹ 100

M.V. = ₹ 120

Dividend = 7% = $\dfrac{7}{100} \times 100$ = ₹ 7

∴ Investment = ₹ 120 and income = ₹ 7.

Income on ₹ 1 = $\dfrac{7}{120}$ = ₹ 0.0583

In company B,

N.V. = ₹ 1000

M.V. = ₹ 1620

Dividend = 8% = $\dfrac{8}{100} \times 1000$ = ₹ 80

∴ Investment = ₹ 1620 and income = ₹ 80.

Income on ₹ 1 = $\dfrac{80}{1620}$ = ₹ 0.0494

Since, rate of income is greater in company A.

∴ Assertion and Reason both are true and Reason is the correct explanation of Assertion.

Hence, Option 1 is the correct explanation.

Assertion (A) : x³ + 2x² - x - 2 is a polynomial of degree 3.

Reason (R) : x + 2 is a factor of the polynomial.

1. Both A and R are correct, and R is the correct explanation for A.

2. Both A and R are correct, and R is not the correct explanation for A.

3. A is true, but R is false.

4. Both A and R are true.

Answer

x³ + 2x² - x - 2 is a polynomial of degree 3.

By factor theorem,

(x - a) is a factor of f(x) if f(a) = 0.

x + 2 = 0

x = -2

Substituting x = -2 in x³ + 2x² - x - 2, we get :

⇒ (-2)³ + 2(-2)² - (-2) - 2

⇒ -8 + 2(4) + 2 - 2

⇒ -8 + 8 + 2 - 2

⇒ 0.

Hence, Option 4 is the correct option.

Assertion (A) : The point (-2, 8) is invariant under reflection in line x = -2

Reason (R) : If a point has its x-coordinate 0, it is invariant under reflection in both axes.

1. Both A and R are correct, and R is the correct explanation for A.

2. Both A and R are correct, and R is not the correct explanation for A.

3. A is true, but R is false.

4. Both A and R are true.

Answer

Point (-2, 8) lies on the line x = -2.

The point which lies on a line is invariant under reflection in the same line.

∴ (-2, 8) is invariant under reflection in line x = -2.

∴ Assertion (A) is true.

If a point has x-coordinate equal to 0 it means it lies on y-axis.

∴ It will be invariant under reflection in y-axis.

∴ Reason (R) is false.

Hence, Option 3 is the correct option.

When a die is cast with numbering on its faces, as shown, the ratio of the probability of getting a composite number to the probability of getting a prime number is ............... .

1. 2 : 3

2. 3 : 2

3. 1 : 3

4. 1 : 2

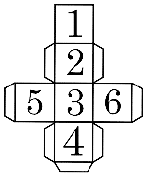
Answer

From numbers 1 to 6

Prime numbers = 2, 3, 5.

Composite numbers = 4, 6.

Probability of getting a prime number = $\dfrac{\text{No. of prime numbers}}{\text{No. of possible outcomes}} = \dfrac{3}{6} = \dfrac{1}{2}$.

Probability of getting a composite number

= $\dfrac{\text{No. of composite numbers}}{\text{No. of possible outcomes}} = \dfrac{2}{6} = \dfrac{1}{3}$.

Probability of getting a composite number to probability of getting a prime number = $\dfrac{1}{3} : \dfrac{1}{2}$ = 2 : 3.

Hence, Option 1 is the correct option.

The product of A = $\begin{bmatrix*}[r] 1 & -2 \\ -3 & 4 \end{bmatrix*}$ and matrix M, AM = B where B = $\begin{bmatrix*}[r] 2 \\ 24 \end{bmatrix*}$, then the order of matrix M is ............... .

1. 2 × 2

2. 2 × 1

3. 1 × 2

4. 4 × 1

Answer

Order of matrix A = 2 × 2

Order of matrix B = 2 × 1

Order of matrix M (let) = a × b

We know that,

Two matrix can be multiplied if the no. of columns of the first matrix is equal to the no. of rows of the second matrix and the resultant matrix has the no. of rows of first matrix and no. of columns of second matrix.

Given,

⇒ AM = B

⇒ A_{2 × 2} × M_{a × b} = B_{2 × 1}

⇒ a = 2 and b = 1.

Order of matrix M = 2 × 1.

Hence, Option 2 is the correct option.

Given, a₁, a₂, a₃, ..... and b₁, b₂, b₃, ..... are real numbers such that a₁ - b₁ = a₂ - b₂ = a₃ - b₃ = ......... are all equal.

a₁ - b₁, a₂ - b₂, a₃ - b₃, ........ forms a ......... progression.

1. Geometric (r = 1)

2. Arithmetic (d = 1)

3. Geometric (r < 1)

4. Arithmetic (d = 0)

Answer

Since,

a₁ - b₁ = a₂ - b₂ = a₃ - b₃.

∴ a₁ - b₁, a₂ - b₂, a₃ - b₃, ........ forms a arithmetic progression with common difference (d = 0).

Hence, Option 4 is the correct option.

Locus of a moving point is ............... if it moves such that it keeps a fixed distance from a fixed point.

1. Circle

2. Line

3. Angle

4. Line segment

Answer

Locus of a moving point is circle if it moves such that it keeps a fixed distance from a fixed point.

Hence, Option 1 is the correct option.

The point of concurrence of the angle bisectors of a triangle is called the ............... of the triangle.

1. centroid

2. incenter

3. circumcenter

4. orthocenter

Answer

The point of concurrence of the angle bisectors of a triangle is called the incenter of the triangle.

Hence, Option 2 is the correct option.