Plot the points A(2, 2) and B(6, -2) in the graph and answer the following :
(a) Reflect points A in origin to point D and write the co-ordinates of point D.
(b) Reflect points A in line y = -2 to point C and write the co-ordinates of point C.
(c) Find a point P on CD which is invariant under reflection in x = 0, write its co-ordinates.
(d) Write the geometrical name of the closed figure ABCD.
(e) Write the co-ordinates of the point of intersection of the diagonals of ABCD.
Answer
The graph is shown below:

(a) From graph,
Co-ordinates of D = (-2, -2).
(b) From graph,
Co-ordinates of C = (2, -6).
(c) Point P(0, -4) lies on y-axis.
∴ It is invariant under reflection in x = 0.
Co-ordinates of P = (0, -4).
(d) From graph,
ABCD is a square.
(e) From graph,
H is the point of intersection of diagonals of ABCD.
Co-ordinates of H = (2, -2).
Plot points A(0, 3), B(4, 0), C(6, 2) and D(5, 0). Reflect the points as given below and write their coordinates :
(a) Reflect A on x-axis to A’.
(b) Reflect B on y-axis to B’.
(c) Reflect C on x-axis to C’.
(d) D remain invariant when reflected on the line whose equation is ............... .
(e) Join the points A, B, C, D, C’, B, A’, B’ and A to form a closed figure. Name the closed figure BCDC’.
Answer
The graph is shown below:

(a) Coordinates of A' = (0, -3).
(b) Coordinates of B' = (-4, 0).
(c) Coordinates of C' = (6, -2).
(d) From graph,
D lies on x-axis.
∴ It is invariant in the line x-axis or y = 0.
D remain invariant when reflected on the line whose equation is y = 0.
(e) From graph,
BCDC' is a concave quadrilateral.
The following data represents the daily wages in rupees of a certain number of employees of a company :
| Daily wages (in ₹) | No. of Employees |
|---|---|
| 30-40 | 8 |
| 40-50 | 14 |
| 50-60 | 12 |
| 60-70 | 17 |
| 70-80 | 20 |
| 80-90 | 26 |
| 90-100 | 13 |
| 100-110 | 10 |
Use a graph to answer the following questions :
(a) Represent the above distribution by an ogive.
(b) Find the following on the graph drawn:
(i) median wage.
(ii) percentage of employees who earn more than ₹ 84 per day.
(iii) number of employees who earn ₹56 and below.
Answer
Cumulative frequency distribution table :
| Daily wages (in ₹) | No. of employees | Cumulative frequency |
|---|---|---|
| 30-40 | 8 | 8 |
| 40-50 | 14 | 22 |
| 50-60 | 12 | 34 |
| 60-70 | 17 | 51 |
| 70-80 | 20 | 71 |
| 80-90 | 26 | 97 |
| 90-100 | 13 | 110 |
| 100-110 | 10 | 120 |
Here, n = 120, which is even.
Median = = 60th term.
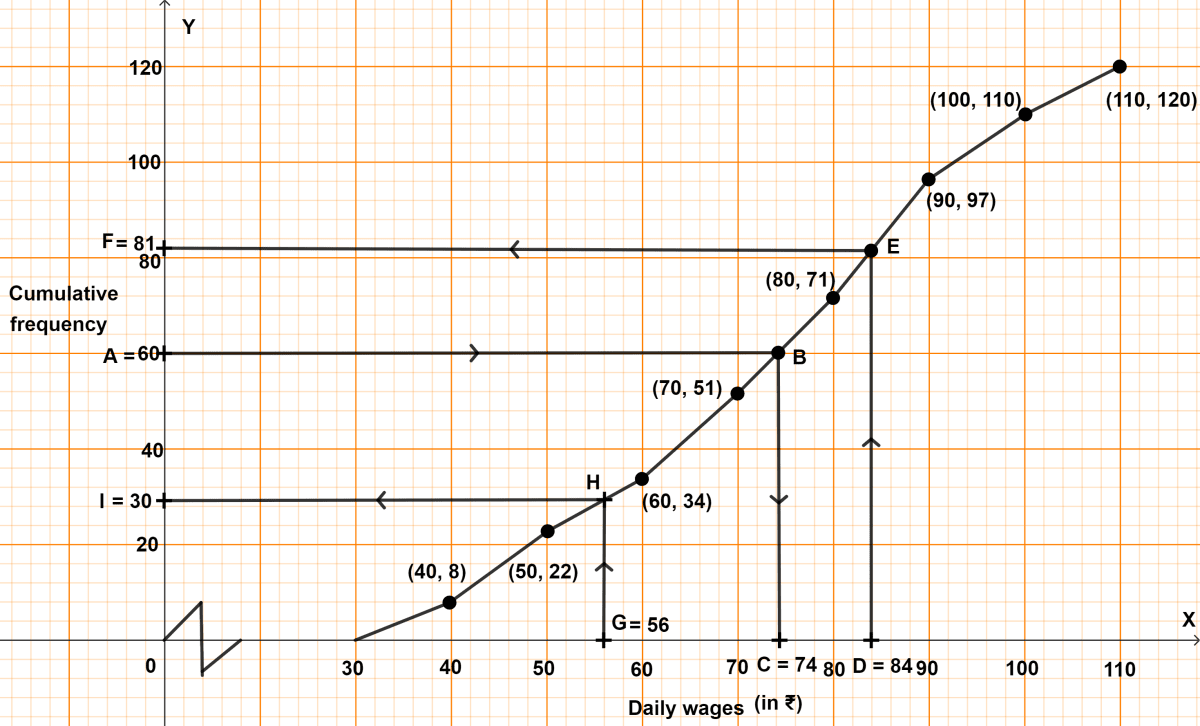
Steps of construction :
1. Plot daily wages on x-axis.
2. Plot cumulative frequency on y-axis.
3. Mark points (40, 8), (50, 22), (60, 34), (70, 51), (80, 71), (90, 97), (100, 110) and (110, 120).
4. Draw a free hand curve passing through the points marked, strating from the lower limit of first class and terminating at upper limit of the last class.
5. Mark A = 60 on y-axis, draw a horizontal line which meets curve at B.
6. Through point B, draw a vertical line which meets x-axis at point C. The value of point C on x-axis is the median. ∴ Median wage is ₹74.
7. Mark D = 84 on x-axis, draw a vertical line which meets curve at E.
8. Through point E, draw a horizontal line which meets y-axis at point F. The value of point F on y-axis represents no. of employees earning less than or equal to ₹ 84 per day.
From graph,
F = 81.
No. of employees earning more than ₹ 84 per day = 120 - 81 = 39.
Percentage of employees earning more than ₹ 84 =
= 32.5 %.
9. Mark G = 56 on x-axis, draw a vertical line which meets curve at H.
10. Through point H, draw a horizontal line which meets y-axis at point I. The value of point I on y-axis represents no. of employees earning less than or equal to ₹ 56 per day.
From graph,
I = 30.
No. of employees earning less than or equal to ₹ 56 per day = 30.
Study the graph and answer the questions that follow :
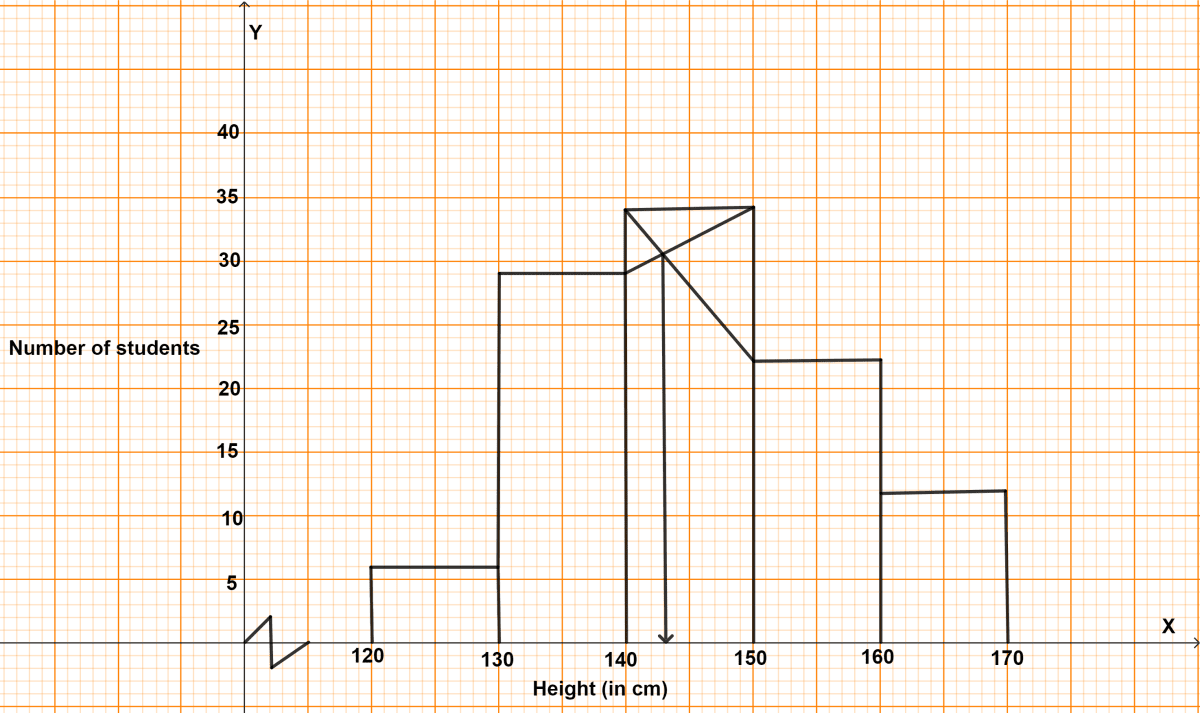
(a) Make a frequency table for the information provided in the graph.
(b) The number of students whose height is less than 150 cm.
(c) The total number of students.
(d) The modal height.
(e) The difference in the modal height and the mean height, if the average height of the students is 145.5 cm.
Answer
(a)
| Class | Frequency (f) | Cumulative frequency (c.f.) |
|---|---|---|
| 120-130 | 6 | 6 |
| 130-140 | 29 | 35 |
| 140-150 | 34 | 69 |
| 150-160 | 22 | 91 |
| 160-170 | 12 | 103 |
(b) From the above table,
The number of students whose height is less than 150 cm = 69.
(c) From the above table,
The total number of students = 103.
(d) From graph,
The modal height = 143 cm.
(e) Mean height = Average height = 145.5
Difference in the modal height and the mean height :
145.5 - 143 = 2.5 cm
Hence, difference between modal height and the mean height = 2.5 cm