Mathematics
If the 6th term of a series in Geometric Progression (G.P.) is 32 and the 9th term is 256, find the:
(a) first term and the common ratio.
(b) sum of its first 10 terms.
G.P.
1 Like
Answer
(a) Let the first term of the Geometric Progression be a and the common ratio be r.
By formula,
Tn = arn
Given,
The 6th term is 32.
⇒ ar6 - 1 = 32
⇒ ar5 = 32 ………(1)
The 9th term is 256.
⇒ ar9 - 1 = 256
⇒ ar8 = 256 ………(2)
Divide equation (2) by (1), we get:
Substitute value of r in equation (1), we get:
Hence, the first term = 1 and common ratio = 2.
(b) By formula,
Substituting values we get :
Hence, sum of the first 10 terms of the G.P. = 1023.
Answered By
1 Like
Related Questions
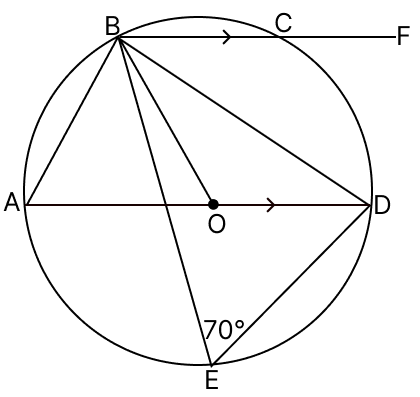
In the adjoining figure of a circle with centre O and diameter AD, ∠BED = 70° and BC is parallel to AD. Find:
(a) ∠BAD
(b) ∠BOD
(c) ∠DBC
(d) ∠DCF
Solve the inequation, write down the solution set and represent it on a real number line:
; x ∈ R
An ice cream cone has a diameter of 7 cm and its height is 9 cm. It is filled with a scoop of spherical shaped ice cream of radius 3.5 cm.
Find: (Give all answers correct to the nearest whole number)

(a) on melting, is the ice cream sufficient to fill the cone completely without any wastage?
(b) the volume of ice cream, if any, is in excess or less.
There are some red, green and white marbles in a box. One marble is picked up at random from this box. If the probability of picking up a red marble is and that of picking up a green marble is then find the :
(a) probability of picking up a white marble.
(b) number of green marbles, if total number of marbles is 54.
(c) probability of not picking up a red marble.