Mathematics
A 20 m high vertical pole and a vertical tower are on the same level ground in such a way that the angle of elevation of the top of the tower, as seen from the foot of the pole, is 60° and the angle of elevation of the top of the pole, as seen from the foot of tower is 30°. Find :
(i) the height of the tower;
(ii) the horizontal distance between the pole and the tower.
Heights & Distances
7 Likes
Answer
(i) Let CD be the tower and AB be the pole,
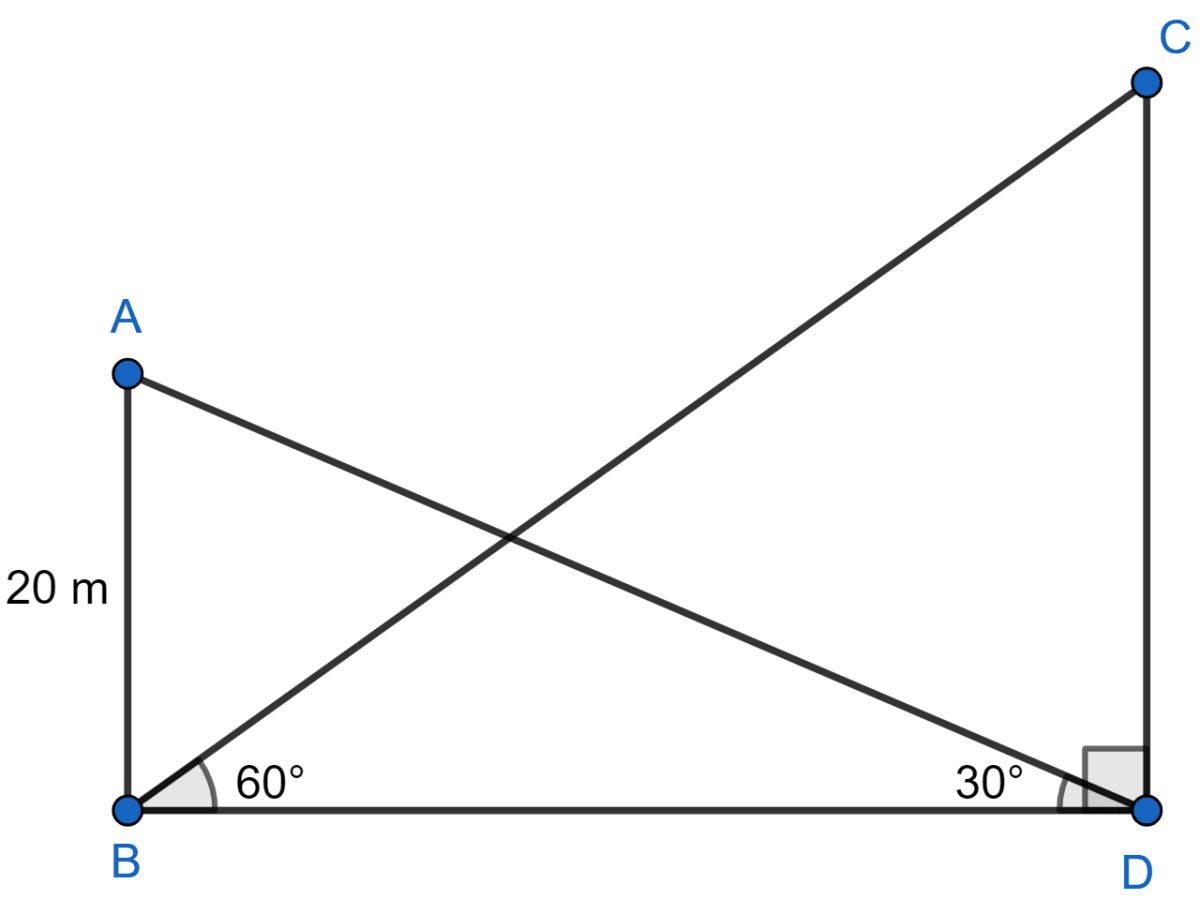
In △ABD,
In △CBD,
Hence, height of tower = 60 meters.
(ii) From part (i),
BD = 34.64 m
Hence, horizontal distance between pole and tower = 34.64 meters.
Answered By
4 Likes
Related Questions
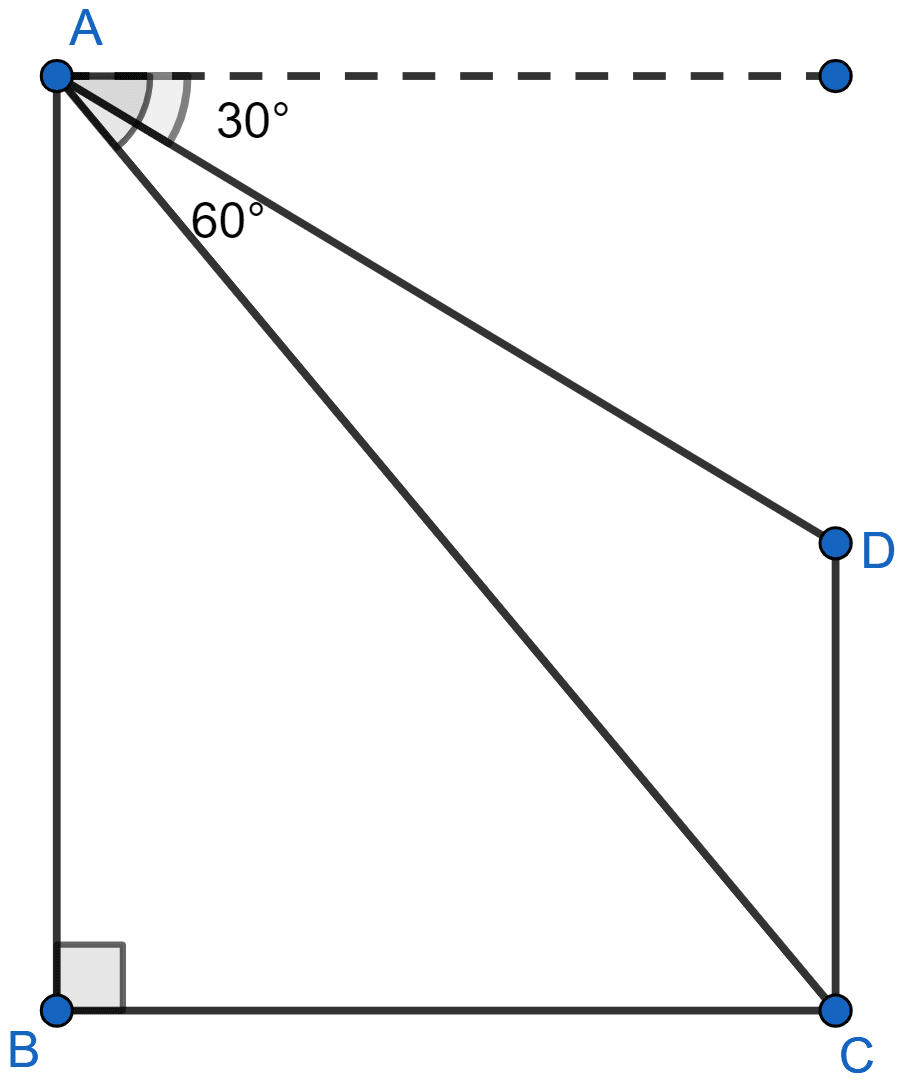
In the given figure, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find :
(i) the horizontal distance between AB and CD.
(ii) the height of the lamp post.
An aeroplane, at an altitude of 250 m, observes the angle of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. If the boats are on the opposite sides of the aeroplane, find the width of the river. Write the answer correct to the nearest whole number.
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the second tower is 30° and 24°, respectively. Find the height of the two towers. Give your answer correct to 3 significant figures.
The angles of depression of two ships A and B as observed from the top of a lighthouse 60 m high are 60° and 45° respectively. If the two ships are on the opposite sides of the lighthouse, find the distance between the two ships. Give your answer correct to nearest whole number.